7: Інтеграція

Last updated
Save as PDF

Page ID: 66651

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустимо, що для даної компанії гранична вартість була визначена як

\[ MC(x)=x^3+3x^2 \nonumber \]

Ми хотіли б реконструювати функцію витрат на основі цих даних. Припустимо, ми також знаємо, що фіксована вартість дорівнює 100 доларів. Як ми дізнаємося вартість на виробництво$x$ виробів?

Почніть з фіксованої вартості.
Додайте граничну вартість для кожного послідовного товару.
Створіть стовпець поточних витрат, щоб відстежувати витрати під час накопичення даних.

Для цього прикладу ми отримаємо:

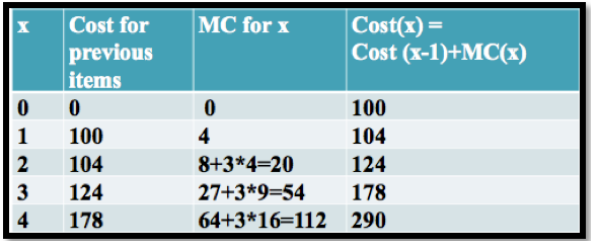
$clipboard_e40ce3222e2315d95e7b88201c2d8dbef.png$

Ми хотіли б пов'язати ці дані з вихідним графіком граничної вартості. Коли ми розглядаємо цей графік, ми бачимо, що орієнтовна вартість фактично відповідає площі під функцією граничної вартості MC (x).

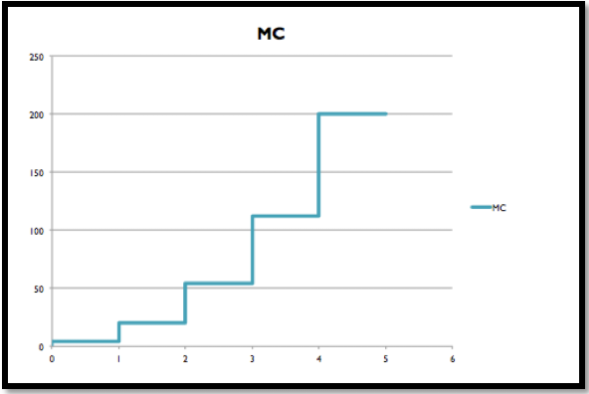
$clipboard_eb078379fdf014832615a6e23a8e6f704.png$

Іншими словами, функція витрат - це накопичення похідної (граничної вартості). Графічно функція витрат відповідає площі під функцією граничних витрат.

Ми хочемо розглянути накопичення неперервних функцій. Мовою числення це називається знаходженням інтеграла.