15.1: Чиста поточна вартість
- Page ID
- 66841
Якщо ви вирішили продовжити курс дій, яка чиста вигода або вартість прийняття цього рішення? Як ви можете систематично визначити, який вибір фінансово перевершує?
Скажімо, ваш відділ маркетингу думає, що він натрапив на наступний гарячий продукт, щоб потрапити на ринок. Орієнтовні витрати на дослідження та розробки сьогодні становлять 10 мільйонів доларів США з очікуваною вартістю пожвавлення в 5 мільйонів доларів за п'ять років. Продукт потрапляє на полиці через два роки. Орієнтовний прибуток на кінець року становить 4 мільйони доларів за перші три роки та 3 мільйони доларів за наступні два роки. У той час стрімкі темпи технології закінчать життєвий цикл нового продукту. Цього минулого року буде заробляти приблизно 1 мільйон доларів прибутку. Кошти, необхідні для цього проекту, будуть отримані на 12% щорічно. Чи має цей проект фінансовий сенс? Ваш колега стверджує, що рішення зрозуміле: ви витратили б 15 мільйонів доларів, щоб заробити 19 мільйонів доларів, тому проект повинен йти вперед. Як ви думаєте?
Аналіз вашого колеги підсумував номінальні цифри. Це явно порушує фундаментальну концепцію часової вартості грошей. У цьому розділі ми розглянемо різні типи інвестиційних рішень і вивчимо методи прийняття оптимальних фінансових рішень.
Що бере участь у прийнятті грошових бізнес-рішень?
Інвестиційні рішення повинні враховувати як тип приймається рішення, так і джерело фінансування, що впливає на процентну ставку, яка використовується при фінансових розрахунках.
Який тип рішення приймається?
Хоча не існує такого поняття, як «стандартне» або «нормальне» рішення, багато бізнес-рішень, здається, підпадають на ті ж три категорії:
- Рішення #1: Прийняття одного вибору з декількох варіантів. Коли ви стикаєтеся з різноманітними варіантами, які вирішать вашу проблему, який варіант фінансово найкращий?
- Рішення #2: Прийняття рішення про те, чи слід проводити один курс дій. Коли ви стикаєтеся лише з одним конкретним курсом дій, ви це робите чи ні?
- Рішення #3: Прийняття декількох варіантів в умовах обмежень. Якщо у вас обмежені ресурси і багато різних можливостей, з яких ви можете вибрати більше одного, як вибрати, які можливості переслідувати, а які пропустити повз?
Яке грошове джерело використовується і що це коштує?
Структура багатьох рішень випливає зі старої прислів'я про те, що вам доведеться витрачати гроші, щоб заробити гроші. Багато курсів дій вимагають інвестицій заздалегідь (витрати) для отримання винагороди (прибутку) у майбутньому. Це означає, що вам потрібно натиснути джерело грошей, перш ніж ви зможете йти вперед з будь-яким курсом дій. Фізичні особи та корпорації можуть отримати доступ до багатьох однакових грошових джерел, але підприємства мають додаткові можливості, які недоступні приватним особам.
- Особисті джерела фінансування. Варіанти отримання грошей у вас обмежені. Як правило, ви можете або скористатися борговим фінансуванням, таким як кредит в банку або кредитна лінія, або ви можете зняти гроші з інвестиційного фонду або ощадного рахунку.
- Якщо ви берете в борг, то фінансова вартість проекту - це процентна ставка, яка нараховується на позикові кошти. Тому, якщо ви фінансуєте проект за допомогою кредиту на 8,5%, що збільшується щорічно, процентна ставка кредиту стає номінальною ставкою, яку ви повинні використовувати в необхідний час розрахунків вартості грошей.
- Якщо ви знімаєте гроші з інвестицій, вартість цього проекту - це процентна ставка, яку ви відмовляєтеся від цих коштів. Наприклад, якщо ви берете гроші з GIC, який заробляє 4% щорічно, ви повинні використовувати процентну ставку GIC в розрахунках рішень.
- Джерела фінансування бізнесу. Підприємства мають значно більше вибору, ніж фізичні особи при отриманні фінансування. Окрім боргового фінансування та поточних інвестицій, підприємства також можуть випускати облігації або використовувати фінансування власного капіталу, наприклад, пропонувати акції компанії. Також можливий бартерінг з діловими партнерами. Однак застосовується той самий принцип: незалежно від процентної ставки джерела фінансування здійснює будь-які розрахунки прийняття рішень.
Фундаментальна концепція часової вартості грошей стверджує, що всі гроші повинні бути переміщені на ту ж дату, перш ніж ви зможете порівняти альтернативи справедливо. Як вже говорилося вище, джерело фінансування, яке ви використовуєте, визначає процентну ставку в цих розрахунках. Якщо ви використовуєте кілька джерел для збору необхідних коштів, ваша процентна ставка є середньозваженим з усіх ставок фінансування заборгованості та власного капіталу, і, звичайно, якщо ви використовуєте одне джерело, то середньозважена ставка просто ставка одного джерела. Зважена процентна ставка відома як вартість капіталу. Цей підручник передбачає, що вартість капіталу при розрахунках ускладнюється щорічно, якщо не вказано інше.
Як прийняти рішення
Підприємства найчастіше приймають рішення, виконуючи один з двох методів: чиста поточна вартість або внутрішні ставки прибутку. Методи чистої поточної вартості засновані на всіх грошових потоках рішення, виражених в сьогоднішніх доларах. На цьому і зосереджена увага даного розділу. Внутрішні норми прибутковості базуються на відсотковому прибутку інвестиції або прибутковості проекту, про який йдеться в наступному розділі.
Метод чистої поточної вартості (\(NPV\)) обчислює різницю між усіма перевагами та витратами для будь-якого даного проекту в сьогоднішніх доларах. Ця методика прийняття рішень обчислює вартість всіх майбутніх потоків доходів і витрат, повернутих до сьогоднішнього дня (що служить координаційною датою). Слово чистий означає, що техніка враховує вкладені гроші, всі витрати або витрати, а також всі винагороди, такі як прибуток у своїх розрахунках. Запам'ятайте ці критерії прийняття розумних\(NPV\) фінансових рішень:
- Якщо чиста поточна вартість більше або дорівнює $0, проект має фінансовий сенс, оскільки він додасть вартості компанії або при мінімальній беззбитковості. Фінансово логічно переслідувати такі типи проектів.
- Якщо чиста поточна вартість менше $0, проект не має фінансового сенсу, оскільки він втратить гроші для компанії. Компанія не має фінансових підстав для реалізації таких типів проектів.
Звичайно, бізнес часто має багато нефінансових причин для переслідування або не проведення певних курсів дій. Ці причини виходять за рамки цього підручника.
Спостерігайте за тим, як\(NPV\) реальні ставки для кожної з трьох поширених типів категорій бізнес-рішень:
- Рішення #1: Прийняття одного вибору з декількох варіантів. Ви повинні вибрати проект з be st\(NPV\). У цьому розділі ви дізнаєтеся техніку, яка допоможе вам вибирати між проектами однакової довжини. Розділ 15.2 вводить ще одну техніку вибору між проектами різної довжини кільця. Наприклад, ви не можете просто використовувати\(NPV\) для порівняння проекту #1, який має чотирирічне життя, проти проекту #2, який має шестирічний термін життя.
- Рішення #2: Вибір, чи слід проводити один курс дій. Ви повинні продовжити проект, якщо po sitive або на мінімальному нулі.\(NPV\)
- Рішення #3: Прийняття декількох варіантів в умовах обмежень. Ви повинні вибрати проекти, які максимально вдаються до талу\(NPV\).
Ця таблиця узагальнює взаємозв'язок між трьома типами рішень та фінансовими критеріями.
| Тип рішення | Фінансові критерії |
|---|---|
| Роблячи один вибір з декількох варіантів | Кращий\(NPV\) |
| Переслідуючи один курс дій | \(NPV\)має бути $0 або вище |
| Роблячи кілька варіантів в умовах обмежень | Поєднання варіантів, що ефективно максимізує загальну\(NPV\) |
Формула
Немає однієї формули розрахунку чистої теперішньої вартості. Однак ви можете представляти\(NPV\) концептуально за допомогою Формули 15.1.

Як це працює
Кожне рішення відрізняється - немає жодного визначеного методу вирішення проблеми. Якби рішення було очевидним, кожен завжди приймав би розумні рішення! Натомість добре вибрати допоможуть три правила переміщення грошей:
- Правило #1: Якщо немає регулярності платежів, то кожна сума являє собою єдиний платіж. Обчислити поточну вартість всіх майбутніх грошових потоків можна тільки за допомогою методів, які ви вивчили в розділі 9 для складної поточної вартості відсотків для разових платежів. Приклад\(\PageIndex{1}\) демонструє це правило.
- Правило #2: Якщо регулярні платежі постійно в тій же сумі, у вас є ситуація ануїтету. Ви можете розрахувати поточну вартість всіх майбутніх грошових потоків, використовуючи методи з глави 11 для складної поточної вартості відсотків для звичайних ануїтетів або ануїтетів. Приклад дозволив\(\PageIndex{1}\) також продемонструвати це правило.
- Правило #3: Якщо регулярні платежі проводяться постійно, але в різних кількостях, то для використання формули вам доведеться обчислити поточну вартість складних процентних одноразових платежів відповідно до Правило #1. Однак те, що відрізняє правило #3 від правила #1, це характеристика «регулярності». За цієї умови, і припускаючи, що у вас є доступ до фінансового калькулятора або електронної таблиці, ця конкретна ситуація представляє метод швидкого доступу, який називається грошовими потоками. Приклад\(\PageIndex{2}\) і приклад\(\PageIndex{3}\) ілюструють ці грошові потоки, які пояснюються далі в цьому розділі.
Важливі зауваження
Коли ви розраховуєте чисту поточну вартість, більшість фінансових прогнозів витрат і вигод є найкращими оцінками. Тому не потрібно бути точним до копійки в остаточному рішенні. Залежно від суми долара, що беруть участь, компанії зазвичай можуть округлити ці розрахунки до найближчих сто або тисяч доларів. Поки немає стандартної практики, цей підручник округляє остаточні рішення до найближчого долара.
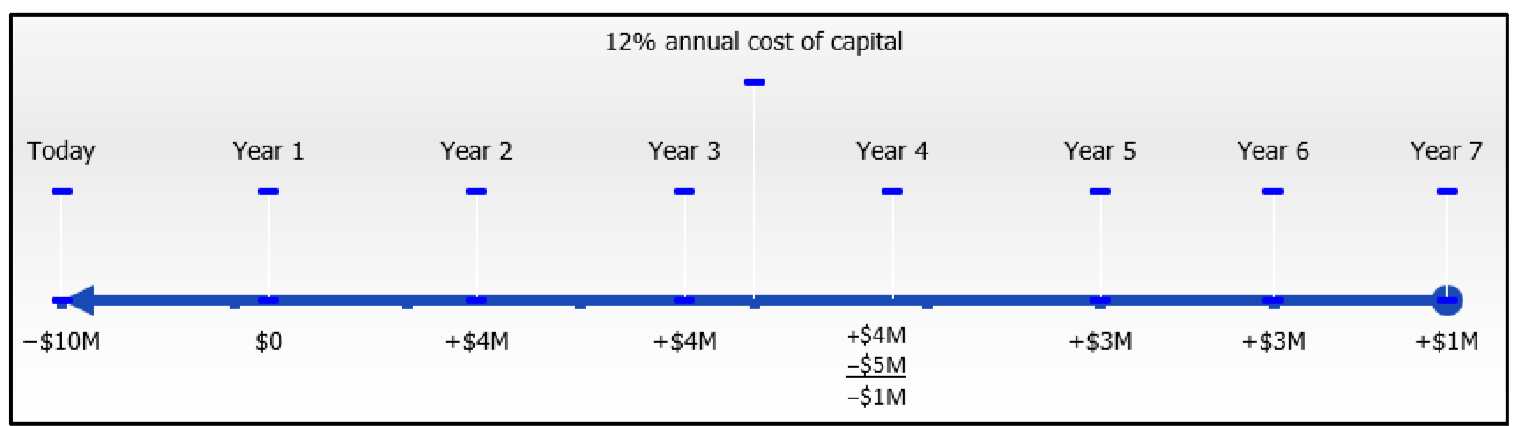
Saggitt Accounting Services потребує регулярного оновлення існуючих комп'ютерних робочих станцій. Якщо він орендує робочі станції на два роки, він зробить виплати на початку місяця в розмірі $1125 без залишкової вартості. Якщо він придбає робочі станції, йому потрібно буде заплатити 26 500 доларів сьогодні, і він може продати обладнання через два роки за 10% від ціни покупки. Потрібно буде позичити ці кошти на два роки під 7,75%, що посилюються щомісяця. Суворо на фінансовій основі, який варіант повинен переслідувати бухгалтерський облік Saggitt? Наскільки краще цей варіант у сьогоднішніх доларах?
Рішення
Оскільки вам потрібно визначитися сьогодні, вам слід обчислити чисту теперішню вартість (\(NPV\)) для кожної альтернативи. Кожен з цих варіантів являє собою вартість, тому ви вибираєте варіант з найменшим\(NPV\).
Що ви вже знаєте
Хронологія покупки відображається на першій шкалі нижче. Що стосується самого банківського кредиту, то розрахунки поточної вартості не потрібні, оскільки поточна вартість всіх платежів по кредиту дорівнює початковому основному кредиту. \(PV_{ORD}\)= $26 500,\(IY\) = 7.75%,\(CY\) = 12,\(FV\) = 10% × $26 500 = $2,650, Роки = 2 Хронологія оренди відображається на другій шкалі нижче. Використовуйте процентну ставку з позики в цьому розрахунку, оскільки Saggitt Accounting в іншому випадку доведеться отримати кредит, якщо він вирішив не здавати в оренду. Тому кредитна ставка являє собою відповідну вартість капіталу. \(PMT\)= $1,125,\(PY\) = 12,\(IY\) = 7,75%,\(CY\) = 12,\(FV\) = 0$, років = 2

Як ви отримаєте
Там Купівля Хронологія:
Крок 1:
Вам потрібно лише перенести виручку з кінця другого року на сьогоднішній день. Це рішення Правило #1. Тому застосуйте формули 9.1, 9.2 та 9.3 для перестановки\(PV\).
Крок 2:
Обчисліть\(NPV\) за формулою 15.1.
Терміни оренди:
Крок 3:
Візьміть належну ренту і перенесіть її на сьогодні. Це рішення Правило #2. Застосовуйте формули 11.1 і 11.5.
Крок 4:
Початкових вкладень немає. Формула 15.1 є тоді\(NPV = PV_{DUE}\).
Крок 5:
Розрахуйте економію, вибравши кращий варіант.

Крок 1:
\[i=7.75 \% / 12=0.6458 \overline{3} \% ; N=12 \times 2=24 \text { compounds } \nonumber \]
\[\$ 2,650=PV(1+0.06458 \overline{3})^{24} \nonumber \]
\[PV=\$ 2,650 \div(1+0.06+58 \overline{3})^{24}=\$ 2,270.63 \nonumber \]
Крок 2:
\[NPV=\$ 2,270.63-\$ 26,500.00=-\$ 24,229.37 \text { or a cost of } \$ 24,229.37 \nonumber \]
Крок 3:
\[N=12 \times 2=24 \text { payments } \nonumber \]
\[PV_{DUE}=\$ 1,125\left[\dfrac{1-\left[\dfrac{1}{\left(1+0.006458 \overline{3}\right)^{\frac{12}{12}}}\right]^{24}}{\left(1+0.006458 \overline{3}\right)^{\frac{12}{12}}}\right] \times\left(1+0.006458 \overline{3}\right)^{\frac{12}{12}}=\$ 25,098.24 \nonumber \]
Крок 4:
\[NPV=\text { cost of } \$ 25,098.24 \nonumber \]
Крок 5:
\[\$ 25,098.24-\$ 24,229.37=\$ 868.87 \text { savings } \nonumber \]
Інструкція калькулятора:
| Транзакція | Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|---|
| Купівля | КІНЕЦЬ | 24 | 7.75 | Відповідь: -2,270.631567 | 0 | 2650 | 12 | 12 |
| Лізинг | ЛВ | \(\surd\) | \(\surd\) | Відповідь: -25 098.23508 | -125 | 0 | \(\surd\) | \(\surd\) |
Якщо Saggitt Accounting Services придбає машину, вона коштуватиме 24 299,37 доларів у сьогоднішніх доларах. Якщо він здасть машину в оренду, це буде коштувати $25 098.24 в сьогоднішніх доларах. Розумний вибір - придбати машину, реалізувавши економію $868.87 в сьогоднішніх доларах.
Регулярний потік грошових потоків
Грошовий потік - це рух грошей в конкретний проект або з нього. Тому кожен раз, коли ви несете витрати або отримуєте вигоду за конкретним проектом, у вас є грошовий потік. За трьома правилами переміщення грошей, як разові платежі, так і ануїтети - це грошові потоки. Ви можете перенести гроші з майбутньої дати на теперішню дату, використовуючи існуючі формули або методи калькулятора.
Третє правило рішення стосується ситуації безперервних регулярних платежів, які є змінними за сумою. Як зазначено в правилі, для вирішення проблеми за формулою вам потрібно буде неодноразово розрахувати складну поточну вартість відсотків (Правило #1). Ця процедура вимагає безлічі повторюваних розрахунків, в яких ви розраховуєте\(N\) і\(PV\) для кожного грошового потоку. Це досить громіздко, оскільки кожен грошовий потік вводить ще два розрахунки та іншу поточну вартість для чистого виходу. І калькулятор, і шаблон Excel спрощують цей процес, зменшуючи як зусилля, так і ймовірність помилки.
Коли ви працюєте з цими безперервними грошовими потоками, де поставити суму на часовій шкалі, залежить від того, чи це вартість чи вигода.
- C Витрати : Якщо не зазначено інше, капітальні витрати витрачаються на початку будь-якого часового сегмента. Таким чином, якщо є капітальні витрати на другий рік, ви можете припустити, що ви понесете їх на початку другого року, що те саме, що і в кінці першого року.
- B benefit s: Доходи, чистий прибуток (продаж продукції за вирахуванням витрат на продукцію) або інші вигоди реалізуються в кінці будь-якого часового сегмента. Таким чином, якщо у другому році є чистий прибуток, ви можете припустити, що реалізуєте їх наприкінці другого року.
Як це працює
Виконайте наступні дії при роботі з регулярними грошовими потоками різної суми:
Крок 1: Намалюйте графік, що ілюструє всі грошові потоки, вартість капіталу та будь-які початкові інвестиції. Завжди малюйте часову шкалу в звичайному форматі ануїтету з усіма транзакціями, що відбуваються в кінці кожного часового інтервалу. Таким чином, будь-які витрати, які ви понесете на початку часового відрізка, розміщуються в кінці попереднього часового відрізка (якщо не зазначено інше).
Крок 2: Для будь-якої конкретної точки на часовій шкалі, в якій існує більше одного грошового потоку, чистий всі грошові потоки в єдине число.
Крок 3: Перемістіть кожен грошовий потік до його теперішньої вартості. Якщо використовуєте формули, розраховуйте періодичну процентну ставку з Формули 9.1. Дотримуйтесь цього розрахунку, неодноразово застосовуючи формули 9.2 (кількість складних періодів для разових платежів) та 9.3 (складні відсотки для разових платежів). В якості альтернативи, якщо використовувати технологію, то застосуйте методику, розглянуту у відповідному розділі нижче.
Крок 4: Чистий результати за допомогою g Формула 15.1, щоб прибути в\(NPV\).
Важливі зауваження
Використання робочого аркуша грошових потоків BAII Plus.
Функція грошових потоків калькулятора вимагає, щоб грошові потоки були регулярними (наприклад, щомісяця, кожного кварталу чи щороку). Суми платежу можуть бути однаковими або змінними. Якщо припущення про регулярність не виконується, не використовуйте функцію грошового потоку; натомість вирішіть проблему за допомогою Правила #1 для одноразових платежів зі складними відсотками.

Фото ілюструє кнопки, що використовуються у функції грошового потоку вашого калькулятора BAII Plus. Доступ до функції грошового потоку, натиснувши CF на клавіатурі. Негайно очистіть пам'ять за допомогою 2nd CLR Work, щоб видалити будь-які раніше введені дані. Використовуйте стрілки ↑ і ↓ для прокрутки різних рядків. Ви повинні суворо дотримуватися угоди про знак грошового потоку та натиснути Enter після введення будь-яких даних.
Ось різні рядки, що з'являються у функції грошового потоку:
- \(CF_o\)= будь-який грошовий потік сьогодні
- \(CXX\)= конкретний грошовий потік, де номер грошового потоку,\(XX\) що починається з 01. Ви повинні вводити грошові потоки в порядку від першого сегмента часу до останнього. Ви не можете пропустити часовий відрізок, навіть якщо він має нульове значення. Кожен часовий відрізок є заповнювачем на часовій шкалі.
- \(FXX\)= періодичність конкретного грошового потоку, де\(XX\) - номер грошового потоку. Саме стільки разів поспіль відбувається відповідна сума грошового потоку. Це дозволяє вводити повторювані суми замість того, щоб вводити їх окремо. За замовчуванням калькулятор встановлює для цієї змінної значення 1.

Після того, як ви ввели всі грошові потоки, ви повинні отримати доступ до інших функцій для генерації вихідних даних. Для чистого теперішнього значення натисніть\(NPV\) на клавіатурі, як показано на фотографії. Це вікно має два рядки:
- \(I\)= відповідність періодичної процентної ставки для інтервалу кожного часового відрізка. Якщо терміни малюються з річними інтервалами, то це повинна бути річна вартість капіталу. Якщо графік малюється з піврічними інтервалами, це повинно бути відповідним піврічним періодичним витратам капіталу.
- \(NPV\)= чиста приведена вартість. Натисніть CPT, щоб розрахувати цю суму. Вихід e охоплює всі майбутні грошові потоки проти будь-яких початкових інвестицій. Цей ключ виконує Формула 15.1.
Речі, на які слід остерігатися
Найпоширенішою помилкою використання калькулятора BAII Plus є неможливість ввести відповідну періодичну процентну ставку у\(NPV\) вікні. Завжди перевіряйте наступне:
- Сукупність на вартість капіталу повинна відповідати інтервалу між грошовими потоками. Якщо ні, перетворіть швидкість, щоб вона збігалася. Наприклад, якщо ваші інтервали піврічні, але вартість капіталу щорічна, ви повинні перетворити вартість капіталу в еквівалентну піврічну складну ставку.
- Застосовуйте Формулу 9.1, обов'язково вводите періодичну ставку, а не номінальну процентну ставку.
Шляхи до успіху
Оскільки грошові потоки можуть бути притоками або відтоками, це дозволяє уникнути плутанини, щоб записати всі цифри з їх грошовими потоками підписати конвенції на часовій шкалі. Це допоможе вам відстежувати різні потоки і мінімізує можливість неправильного взаємозв'язку з усіма наявними значеннями.
Якщо обчислюється від'ємна чиста поточна вартість, чи означає це, що проект збитковий?
- Відповідь
-
Ні, це означає, що проект не може повернути свої інвестиції та вартість капіталу. Якщо компанія зможе досить знизити свою вартість капіталу, то чиста приведена вартість фактично може стати позитивною
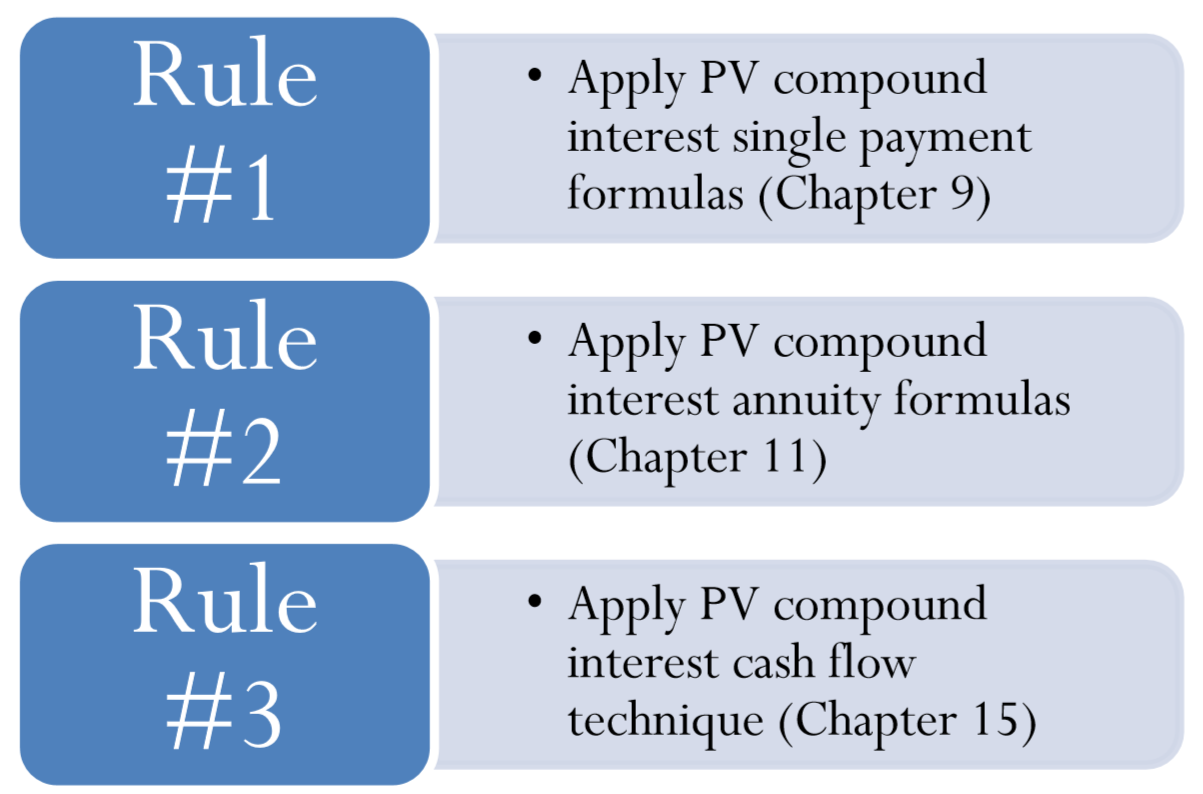
Повторно перегляньте запуск нового продукту, розглянутий у сценарії відкриття в цьому розділі. Нагадаємо, що витрати на дослідження та розробки сьогодні становлять 10 мільйонів доларів, а очікувана вартість пожвавлення в 5 мільйонів доларів на п'ятий рік. Очікується, що продукт надійде в продаж, починаючи з двох років і, за прогнозами, принесе прибуток на кінець року в розмірі 4 мільйонів доларів за перші три роки та ще 3 мільйони доларів на рік протягом наступних двох років. Його останній рік дозволить отримати прогнозований $1 млн прибутку. Вартість капіталу для цього проекту становить 12% щорічно. Тільки з фінансової точки зору, чи повинен бути запущений цей новий продукт?
Рішення
У вас є грошові потоки на різні дати. Для того, щоб прийняти рішення сьогодні, вам слід перенести всі гроші на сьогоднішній день і розрахувати чисту поточну вартість (\(NPV\)).
Що ви вже знаєте
Кроки 1 і 2:
Графік запуску запропонованого продукту відображається нижче.
\[IY=12 \%, CY=1, PV=-\$ 10 M \nonumber \]
Майбутні грошові потоки відображаються на часовій шкалі. Відзначимо, що вартість в п'ятий рік припадає на початок року, що і на кінець четвертого року.
Як ви туди потрапите
Крок 3:
Розрахуйте періодичну процентну ставку за допомогою Формули 9.1. Для кожного грошового потоку розрахуйте приведену вартість за формулами 9.2 і 9.3, переставляючи для\(PV\).
\[\begin{array}{l}{i=12 \% / 1=12 \%} \\ {\text { Cash Flow } 1: N=1 \times 2=2 \text { compounds; } P V=\$ 4,000,000 \div(1+0.12)^{2}=\$ 3,188,775.51} \\ {\text { Cash Flow } 2: N=1 \times 3=3 \text { compounds; } P V=\$ 4,000,000 \div(1+0.12)^{3}=\$ 2,847,120.991} \\ {\text { Cash Flow } 3: N=1 \times 4=4 \text { compounds; } P V=-\$ 1,000,000 \div(1+0.12)^{5}=\$ 1,702,280.567} \\ {\text { Cash Flow } 4: N=1 \times 5=5 \text { compounds; } P V=\$ 3,000,000 \div(1+0.12)^{6}=\$ 1,519,893.367} \\ {\text { Cash Flow } 6: N=1 \times 7=7 \text { compounds; } P V=\$ 1,000,000 \div(1+0.12)^{7}=\$ 452,349.2153}\end{array} \nonumber \]
Крок 4:
Розрахуйте\(NPV\) за допомогою Формули 15.1.
\[\begin{aligned} NPV &=(\$ 3,188,775.51+\$ 2,847,120.991-\$ 635,518.0784+\$ 1,702,280.567+\$ 1,519,893.364+ \$ 452,349.2153)-\$ 10,000,000\\&=\$ 9,074,901.569-\$ 10,000,000\\&=-\$ 925,098.43\\ &==>-\$ 925,098 \end{aligned} \nonumber \]
Виконувати
Крок 3:
\(i\)= 12% /1 = 12%
\ [\ почати {вирівняний}
&\ текст {Грошовий потік} 1: N = 1\ раз 2 = 2\ текст {сполуки;} PV=\ $4,000,000\ div (1+0,12) ^ {2} =\ $3,188,775.51\\
&\ text {Грошовий потік} 2: N = 1\ раз 3=3\ текст {сполуки;} PV =\ $4,000,000\ div 1+0,12) ^ {3} =\ $2,847,120.991\\
&\ текст {Готівковий розрахунок Потік} 3: N = 1\ раз 4 = 4\ текст {сполуки;} PV=-\ $1,000,000\ div (1+0,12) ^ {4} =-\ $635,518.0784\\
&\ текст {грошовий потік} 4: N = 1\ раз 5=5\ текст {сполуки;} PV =\ $3,000,000$\ div (1+0.12) ^ {5} = 1,702,280,567\\
&\ текст {Грошовий потік} 5: N = 1\ раз 6=6\ текст {сполуки;} PV=\ $ 3 000\ div (1+0,12) ^ {6} =\ $1,519,893.364\\
&\ text {Грошовий потік} 6: N = 1\ раз 7=7\ текст {сполуки;} PV=\ $1,000,000\ div (1+0,12) ^ {7} =\ $452 349.2153
\ кінець {вирівняний}\ nonumber\]
Крок 4:
\[\begin{aligned} NPV &= (\$3,188,775.51 + \$2,847,120.991 − \$635,518.0784 + \$1,702,280.567 + \$1,519,893.364 + \$452,349.2153) − \$10,000,000 \\ &= \$9,074,901.569 − \$10,000,000\\ &= −\$925,098.43 \\ &==> −\$925,098 \end{aligned} \nonumber \]
Інструкції з калькулятора
| Грошові потоки | ||
|---|---|---|
| Грошовий потік | Сума (\(CXX\) | Частота (\(FXX\)) |
| ФІНАНСОВИЙ ДИРЕКТОР | -10000000 | Н/Д |
| С01 & Ф01 | 0 | 1 |
| С02 & Ф02 | 4000000 | 2 |
| С03 & Ф03 | -1000000 | 1 |
| С04 & Ф04 | 3000000 | 2 |
| С05 & Ф05 | 1000000 | 1 |
| НПВ | |
|---|---|
| Я | НПВ |
| 12 | Відповідь: -925 098.4309 |
Якщо прогнозовані витрати та прибутки є достатньо точними, то новий продукт не слід запускати за поточної фінансової структури, оскільки його чиста поточна вартість становить -925 098 доларів США. Це означає, що прибуток не в змозі повернути необхідні інвестиції разом із вартістю капіталу.
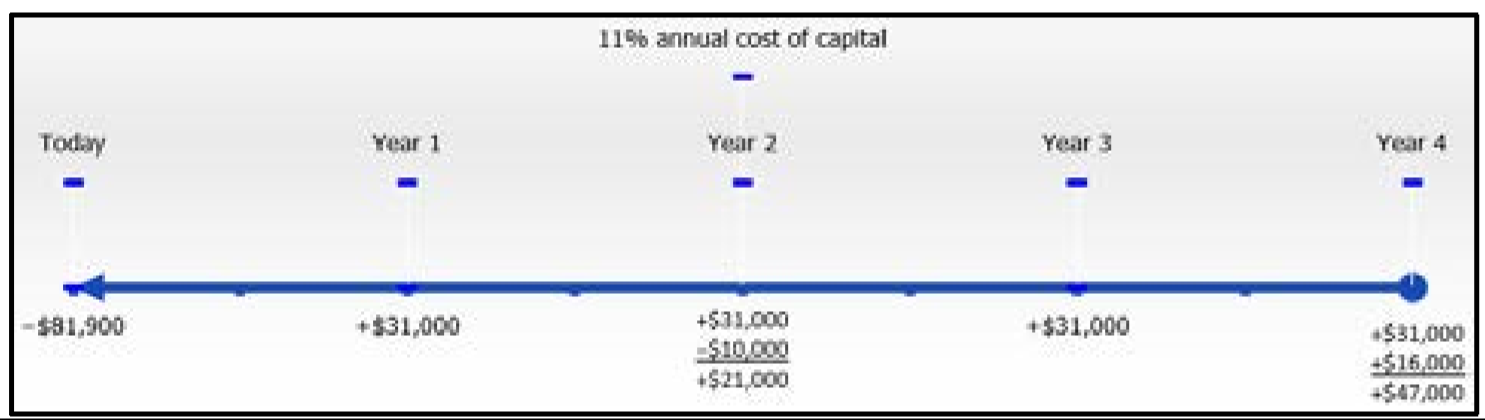
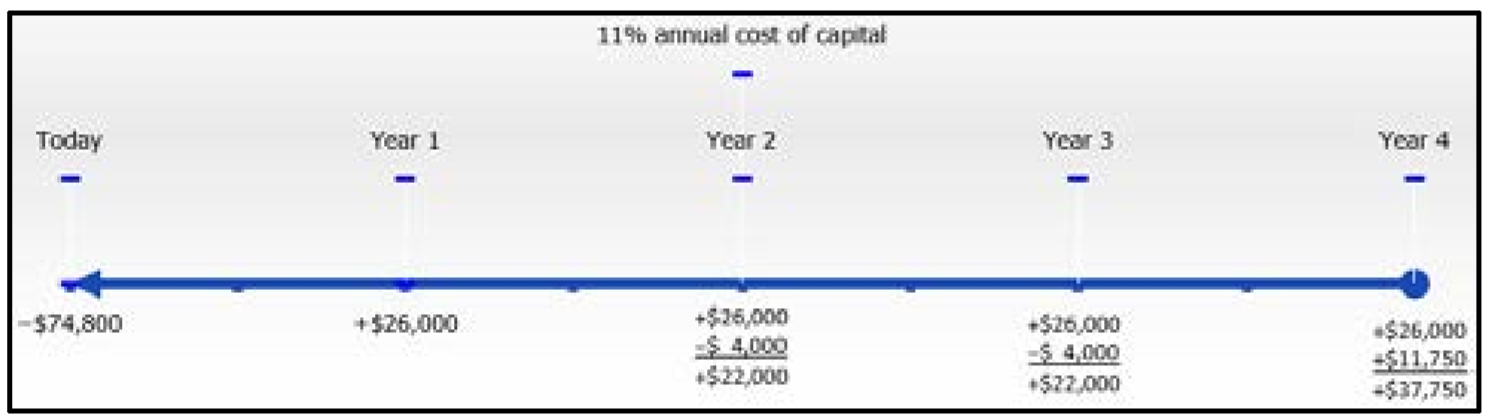
Lethbridge Community College розглядає можливість придбання нового промислового обладнання для ксерокс і звузив вибір до двох порівнянних машин Xerox і Canon. Машина Xerox може бути придбана за $81 900 сьогодні і, як очікується, матиме термін служби чотири роки з економією 31 000 доларів праці та матеріалів щороку. Очікується, що пакет технічного обслуговування в розмірі 10 000 доларів буде придбаний на початку третього року, а машина може бути продана за 16 000 доларів після чотирьох років. Машина Canon продається за 74,800 доларів і, за прогнозами, заощадить 26 000 доларів праці та матеріалів щороку. Процедура технічного обслуговування $4,000 необхідна на початку обох років три і чотири. Залишкова вартість машини оцінюється в $11 750. Вартість капіталу становить 11%. Яку машину слід придбати, і скільки грошей вона заощадить над альтернативою?
Рішення
Для кожного ксерокс у вас є грошові потоки на різні дати. Для того, щоб прийняти рішення сьогодні, ви повинні перенести всі гроші на сьогодні і розрахувати чисту поточну вартість (\(NPV\)) для кожного ксерокс.
Що ви вже знаєте
Кроки 1 і 2:
Терміни для кожного фотоапарата відображаються нижче (Xerox ліворуч, Canon праворуч).
Xerox:\(IY=11 \%, CY=1, PV=-\$ 81,900\) майбутні грошові потоки відображаються на часовій шкалі.
Canon:\(IY=11 \%, CY=1, PV=-\$ 74,800\) майбутні грошові потоки відображаються на часовій шкалі.
Відзначимо, що витрати, що відбуваються на початку року, фіксуються в кінці попереднього року.
Як ви туди потрапите
Крок 3:
Розрахуйте періодичну процентну ставку за формулою 9.1. Для кожного ксерокс розрахуйте поточну вартість кожного грошового потоку за формулами 9.2 і 9.3, переставляючи для\(PV\).
Крок 4:
Для кожного ксерокс розрахуйте\(NPV\) за допомогою Формули 15.1.
Крок 5:
Розрахуйте економію, вибравши кращий варіант.
Виконувати
Крок 3:
\[i=11 \% / 1=11 \% \nonumber \]
ксерокс:
\[\begin{array}{l}{\text { Cash Flow } 1: N=1 \times 1=1 \text { compounds; } PV=\$ 31,000 \div(1+0.11)^{1}=\$ 27,927.\overline{927}} \\ {\text { Cash Flow } 2: N=1 \times 2=2 \text { compounds; } PV=\$ 21,000 \div(1+0.11)^{2}=\$ 17,044.0711} \\ {\text { Cash Flow } 3: N=1 \times 3=3 \text { compounds; } PV=\$ 31,000 \div(1+0.11)^{3}=\$ 22,666.93282} \\ {\text { Cash Flow } 4: N=1 \times 4=4 \text { compounds; } PV=\$ 47,000 \div(1+0.11)^{4}=\$ 30,960.35578}\end{array} \nonumber \]
Крок 4:
\[\begin{aligned} NPV &=(\$ 27,927.\overline{927}+\$ 17,044.0711+\$ 22,666.93282+\$ 30,960.35578)-\$ 81,900 \\ &=\$ 98,599.28763-\$ 81,900\\ &=\$ 16,699.29\\ &==>\$ 16,699 \end{aligned} \nonumber \]
Канон:
\[\begin{array}{l}{\text { Cash Flow } 1: N=1 \times 1=1 \text { compounds; } PV=\$ 26,000 \div(1+0.11)^{1}=\$ 23,423 . \overline{423}} \\ {\text { Cash Flow } 2: N=1 \times 2=2 \text { compounds; } PV=\$ 22,000 \div(1+0.11)^{2}=\$ 17,855.69353} \\ {\text { Cash Flow } 3: N=1 \times 3=3 \text { compounds; } PV=\$ 22,000 \div(1+0.11)^{3}=\$ 16,086.21039} \\ {\text { Cash Flow } 4: N=1 \times 4=4 \text { compounds; } PV=\$ 37,750 \div(1+0.11)^{4}=\$ 24,867.09427}\end{array} \nonumber \]
Крок 4:
Канон:
\[\begin{aligned} NPV &=(\$ 23,423.\overline{423}+\$ 17,855.69353+\$ 16,086.21039+\$ 24,867.09427)-\$ 74,800 \\ &=\$ 82,232.42162-\$ 74,800\\ &=\$ 7,432.42\\ &==>\$ 7,432 \end{aligned} \nonumber \]
Xerox має більш високу економію\(\$16,699 − \$7,432 = \$9,267\)
Крок 5:
Xerox має вищу економію на $16,699 − $7,432 = $9,267
Інструкції з калькулятора
| Грошові потоки | ||||
|---|---|---|---|---|
| Ксерокс | Canon | |||
| Грошовий потік | Сума (\(CXX\) | Частота (\(FXX\)) | Сума (\(CXX\) | Частота (\(FXX\)) |
| ФІНАНСОВИЙ ДИРЕКТОР | -81900 | Н/Д | -74800 | Н/Д |
| С01 & Ф01 | 31000 | 1 | 26000 | 1 |
| С02 & Ф02 | 21000 | 1 | 22000 | 2 |
| С03 & Ф03 | 31000 | 1 | 37750 | 1 |
| С04 & Ф04 | 47000 | 1 | ||
| НПВ | ||
|---|---|---|
| Ксерокс | Canon | |
| Я | 11 | 11 |
| НПВ | Відповідь: 16 699.28763 | Відповідь: 7,432.421617 |
Виходячи з передбачуваних витрат, технічного обслуговування та економії, ксерокс Xerox слід придбати, оскільки це призводить до очікуваної економії 8,867 доларів у сьогоднішніх доларах. Машина Xerox представляє поточний грошовий потік у розмірі 16 299 доларів, тоді як Canon - 7 432 доларів.
Робота з обмеженими ресурсами
В ідеальному фінансовому світі ви завжди повинні проводити будь-який проект з позитивною чистою поточною вартістю, оскільки це рішення призводить до фінансової вигоди. Однак ніхто, будь то окрема особа або велика корпорація або уряд, фактично не має доступу до необмежених ресурсів для фінансування всіх її потенційних проектів. Якби такі необмежені ресурси існували, проблеми світу можна було б вирішити за добу!
Зазвичай в житті є багато шляхів, які ви можете вибрати, кожен зі своїми достоїнствами. Ці шляхи не обов'язково є взаємовиключними, тому ви можете вибрати більше одного. Однак наявність обмежених ресурсів означає, що ви не можете переслідувати всі ці шляхи. Наприклад, можливо, PepsiCo дізнався за допомогою маркетингових досліджень, що може випустити 15 нових смаків і видів безалкогольних напоїв. Кожен із цих смаків та видів вимагає величезних виробничих ресурсів, вимог до робочої сили та маркетингової підтримки, щоб вивести його на ринок. Але навіть така величезна компанія, як PepsiCo, не має ресурсів для реалізації всіх цих можливостей. Який з них він вибирає?
Для вирішення використовується процес, який називається жорстким нормуванням капіталу. Цей процес вимагає від вас обчислити чисту поточну вартість кожного можливого проекту, а потім ефективно розподілити свої обмежені капітальні ресурси для проектів, щоб максимізувати сукупну чисту поточну вартість. З фінансової точки зору ви не розглядаєте жодних проектів з негативною чистою теперішньою вартістю.
Формула
Метою вибору декількох варіантів є максимізація чистої теперішньої вартості. При виборі цих різних варіантів несправедливо порівнювати проекти різної величини, просто дивлячись на їх\(NPV\). Можна було б очікувати, що проект, що вимагає інвестицій у розмірі 10 мільйонів доларів, повинен виробляти набагато більший\(NPV\), ніж проект, що вимагає інвестицій у розмірі 10 000 доларів. Замість цього, це правильно, щоб вивчити ефективне використання цих обмежених ресурсів, або подивитися на «вибух за ваш долар». Для цього потрібно обчислити коефіцієнт чистого теперішньої вартості, показаний у Формулі 15.2.

Як це працює
Виконайте наступні дії, щоб виконати жорстке нормування капіталу:
Крок 1: Визначте бюджетні обмеження.
Крок 2: Якщо ще не відомо, обчисліть чисту теперішню вартість (\(NPV\)) для кожного з доступних проектів за формулою 15.1.
Крок 3: Обчисліть коефіцієнт чистої поточної вартості для кожного проекту за формулою 15.2.
Крок 4: Оцініть проекти від найвищого до найнижчого коефіцієнта, зазначивши початковий грошовий потік, необхідний для кожного проекту.
Крок 5: Починаючи з проекту з найвищим коефіцієнтом чистої поточної вартості та прогресуючи за рейтинговим списком проектів, оцініть різні комбінації проектів та їх загальну суму, щоб\(NPV\) загальні початкові грошові потоки залишалися в межах бюджетних обмежень.
Крок 6: Виберіть комбінацію, яка максимізує т він\(NPV\).
Важливі зауваження
Ця методика робить припущення, що кожен з розглянутих проектів не залежить від інших. Іншими словами, вибір одного конкретного проекту або шляху не заважає вибрати інший проект або шлях. Існують набагато більш просунуті методики оптимізації списку проектів. Ці методи включають науки про управління або методи лінійного програмування. Однак ці прийоми виходять за рамки цього підручника, який зосереджується просто на основних принципах, що лежать в основі цього рішення.
Шляхи до успіху
Завершуючи крок 5 процесу, завжди вибирайте найвищі\(NPV_{RATIO}\) проекти в порядку, поки не досягнете точки, коли решта бюджету стане проблемою. Іншими словами, лише в той момент, коли вибір наступного рангового проекту виключає з розгляду проект з нижчим рейтингом, вам потрібно почати вивчати різні можливі комбінації. У більшості типових ситуацій оптимальна комбінація включає в себе всі pr об'єкти, обрані до цієї критичної точки.
Nygard International визначив кілька проектів, які вона може здійснювати, як зазначено в таблиці нижче. Поточні фінанси компанії дозволяють бюджет капіталу в розмірі 1,25 мільйона доларів. Які проекти повинні бути здійснені?
| Проект | Початковий грошовий потік | Чиста поточна вартість |
|---|---|---|
| Автоматизуйте виробничий процес | $428 000 | $214,000 |
| Запустіть нову моду A | $780 000 | 550 000 доларів |
| Заміна техніки в розподільному центрі | $150 000 | $175,000 |
| Запустіть нову моду B | $395,000 | $610 000 |
| Розширити торгову точку | $145,000 | $245,000 |
| Переглянути процеси доставки | $282,000 | $420 000 |
Рішення
Вам потрібно виконати жорстке нормування капіталу, щоб\(NPV\) максимізувати ваш обмежений бюджет. Для цього потрібно обчислити коефіцієнт чистої поточної вартості (\(NPV_{RATIO}\)) для кожного проекту.
Що ви вже знаєте
Крок 1:
Загальний доступний бюджет становить 1,25 мільйона доларів.
Крок 2:
Чисті теперішні значення наведені в таблиці.
Як ви туди потрапите
Крок 3:
Розрахуйте коефіцієнт чистої поточної вартості для кожного проекту за формулою 15.2.
Кроки з 4 по 6:
Оцініть\(NPV_{RATIO}\) від найвищого до найнижчого, оцініть бюджет і доступні комбінації, а потім виберіть можливість, яка максимізує\(NPV\).
Виконувати
Кроки з 3 по 5:
\(NPV_{RATIO}\)Наведена в таблиці нижче. Проекти сортуються за спаданням. Кілька розрахунків, перерахованих нижче в таблиці, показують, як\(NPV_{RATIO}\) розраховується. Зауважте, що після вибору першого проекту, якщо ви обираєте другий проект, це призведе до ліквідації п'ятого проекту, оскільки його початковий грошовий потік перевищує решту бюджету ($1,250 000 − $145 000 − $395 000 = 710 000$). Тому ви завжди включаєте перший проект у свої комбінації і повинні вивчити різні аранжування наступних п'яти проектів.
| Проект | Початковий грошовий потік | Чиста поточна вартість | Чистий коефіцієнт поточної вартості | Деякі можливі комбінації | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| Розширити торгову точку | $145,000 | $245,000 | (1) 1.69 | . | . | . | . | . |
| Запустіть нову моду B | $395,000 | $610 000 | (2) 1.54 | . | . | . | ||
| Переглянути процеси доставки | $282,000 | $420 000 | 1.49 | . | . | . | . | |
| Заміна техніки в розподільному центрі | $150 000 | $175,000 | 1.17 | . | . | . | ||
| Запустіть нову моду A | $780 000 | 550 000 доларів | 0,71 | . | ||||
| Автоматизуйте виробничий процес | $428 000 | $214,000 | 0,50 | . | . | . | ||
(1)\(NPV_{RATIO}=\dfrac{\$ 245,000}{\$145,000}=1.69 \nonumber\)
(2)\(NPV_{RATIO}=\dfrac{\$ 610,000}{\$395,000}=1.54 \nonumber\)
| Комбінації | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Загальний бюджет | (1) 972 000 доларів | 1 250 000 доларів | 1 1,118 000 доларів | 1 005,000$ | 1 207 000 доларів |
| Всього\(NPV\) | (2) 1 450 000 доларів | 1 489 000$ | 1 244 000 доларів | 1 054 000 доларів | 1 215 000$ |
(1) $145 000 + $395,000 + $282,000 + $150 000 = 972 000 доларів
(2) $245,000 + $610,000 + $420,000 + $175 000 = 1 450 000 доларів
Крок 6:
Комбінація #2 пропонує\(NPV\) найвищий $1,489,000.
Після того, як проекти ранжуються від найвищого до найнижчого\(NPV\) коефіцієнта, «Розширити торгову точку» запропонував найвищий коефіцієнт і вибирається. Комбінація #2, що складається з «Розширення роздрібної торгової точки», «Запустіть нову моду B», «Переглянути процеси доставки» та «Автоматизувати виробничий процес», пропонує найвищий\(NPV\) $1,489 000 і використовує повний капітал бюджету в розмірі 1 250 000 доларів США.
