18.2: Опис однієї мережі

Більшість соціологів мають розумні робочі знання базової уніваріативної та двоваріантної описової та інференційної статистики. Багато з цих інструментів знаходять негайне застосування в роботі з даними соціальних мереж. Є, однак, дві досить важливі відмінні риси застосування цих інструментів до мережевих даних.

По-перше, і найважливіше, аналіз соціальних мереж стосується відносин між суб'єктами, а не про відносини між змінними. Більшість соціологів вивчили свою статистику за допомогою додатків до вивчення розподілу балів акторів (випадків) за змінними та зв'язків між цими розподілами. Дізнаємося про середнє значення набору балів за змінною «дохід». Дізнається про коефіцієнт кореляції добутку нульового порядку Пірсона для індексації лінійної асоціації між розподілом доходів актора та освітнім досягненням актора.

Застосування статистики до соціальних мереж також стосується опису розподілів та відносин між дистрибутивами. Але, замість того, щоб описувати розподіли атрибутів акторів (або «змінних»), ми переймаємося описом розподілів відносин між акторами. Застосовуючи статистику до мережевих даних, ми стурбовані такими питаннями, як середня сила відносин між суб'єктами; нас хвилюють питання на кшталт «чи сила зв'язків між суб'єктами мережі корелює з центральністю акторів у мережі?» Більшість описових статистичних інструментів однакові для аналізу атрибутів та для реляційного аналізу - але предмет зовсім інший!

По-друге, багато інструментів стандартної інференційної статистики що ми дізналися з вивчення розподілів атрибутів не застосовуються безпосередньо до мережевих даних. Більшість стандартних формул для обчислення оціночних стандартних помилок, обчислення тестової статистики та оцінки ймовірності нульових гіпотез, які ми дізналися в базовій статистиці, не працюють з мережевими даними (і, якщо вони використовуються, можуть давати нам «хибнопозитивні» відповіді частіше, ніж «помилково негативні»). Це пов'язано з тим, що «спостереження» або бали в мережевих даних не є «незалежними» вибірками з популяцій. При аналізі атрибутів часто дуже розумно припустити, що дохід Фреда та освіта Фреда - це «випробування», яке не залежить від доходу Сью та освіти Сью. Ми можемо ставитися до Фреда і Сью як до самостійних реплікацій.

У мережевому аналізі ми орієнтуємося на відносини, а не на атрибути. Отже, одне спостереження цілком може бути краваткою Фреда з Сью; іншим спостереженням може бути зв'язок Фреда з Джорджем; ще одним може бути зв'язок Сью з Джорджем. Це не «самостійні» реплікації. Фред бере участь у двох спостереженнях (як і Сью і Джордж), мабуть, не розумно припускати, що ці відносини є «незалежними», оскільки вони обидва залучають Джорджа.

Стандартні формули для обчислення стандартних помилок і інференційних тестів на атрибути, як правило, припускають незалежні спостереження. Застосування їх, коли спостереження не є незалежними, може бути дуже оманливим. Замість цього використовуються альтернативні числові підходи до оцінки стандартних помилок для мережевої статистики. Ці «завантажувальні обв'язки» (і перестановки) підходи обчислюють розподіл вибірки статистики безпосередньо з спостережуваних мереж, використовуючи випадкове присвоєння через сотні або тисячі випробувань за припущенням, що нульові гіпотези вірні.

Ці загальні моменти стануть зрозумілішими, коли ми розглянемо деякі реальні випадки. Отже, почнемо з найпростішої уніваріативної описової та інференційної статистики, а потім перейдемо до дещо більш складних завдань.

Уніваріативна описова статистика

Для більшості прикладів у цьому розділі ми знову зупинимося на наборі даних Knoke, який описує два відносини обміну інформацією та обміну інформацією гроші серед десяти організацій, що працюють у сфері соціального забезпечення. На малюнку 18.1 перераховані ці дані.

Малюнок 18.1: Лістинг (Data>Display) матриць інформації та обміну грошима Knoke

Ці конкретні дані бувають асиметричними та двійковими. Більшість статистичних інструментів для роботи з мережевими даними можуть бути застосовані як до симетричних даних, так і до даних, де оцінюються відносини (міцність, вартість, ймовірність краватки). Як і будь-яка описова статистика, масштаб вимірювання (двійковий або цінний) має значення при правильному виборі щодо інтерпретації та застосування багатьох статистичних інструментів.

Дані, які аналізуються за допомогою статистичних інструментів, коли ми працюємо з мережевими даними, є спостереженнями про відносини між суб'єктами. Отже, в кожній матриці ми маємо 10 х 10 = 100 спостережень або випадків. Для багатьох аналізів зв'язки акторів з собою (головна діагональ) не мають сенсу, і не використовуються, тому було б\(\left( N * N - 1 = 90 \right)\) observations. If data are symmetric (i.e. \(X_{ij} = X_{ji}\)), half of these are redundant, and wouldn't be used, so there would be \(\left( N * N - 1 / 2 = 45 \right)\) observations.

Те, що ми хотіли б узагальнити з нашою описовою статистикою, - це деякі характеристики розподілу цих балів. Інструменти>Уніваріативна статистика може бути використано для генерації найбільш часто використовуваних заходів для кожної матриці (вибрати матрицю в діалоговому вікні і вибрати, чи слід включають діагональ). На малюнку 18.2 наведені результати для нашого прикладу дані, виключаючи діагональ.

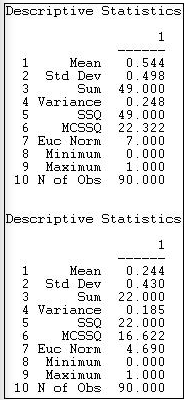
Малюнок 18.2: Уніваріативна описова статистика для інформації Knoke та цілих грошових мереж

Що стосується зв'язку обміну інформацією, ми бачимо, що ми маємо 90 спостережень, які варіюються від мінімального балу нуля до максимуму одиниці. Сума стяжок дорівнює 49, а середнє значення стяжок 49/90 = .544. Оскільки відношення було закодовано як «фіктивна» змінна (нуль для жодного відношення, один для відношення), середнє значення також є часткою можливих зв'язків, які присутні (або щільність), або ймовірність того, що будь-який заданий зв'язок між двома випадковими акторами присутній (шанс 54,4%).

Наведено також кілька заходів мінливості розподілу. Обчислюються суми квадратних відхилень від середнього, дисперсії та стандартного відхилення - але є більш значущими для цінних, ніж двійкові дані. Також передбачена евклідова норма (яка є квадратним коренем суми значень в квадраті). Однією мірою не дано, але іноді корисним є коефіцієнт варіації (стандартне відхилення/середній час 100) дорівнює 91,5. Це говорить про досить багато варіацій у відсотках від середнього балу. UCINET не надає жодної статистики щодо розподільної форми (перекосу або куртозу).

Швидке сканування говорить нам, що середнє значення (або щільність) для обміну грошей нижче, і має трохи меншу мінливість.

Окрім вивчення всього розподілу зв'язків, ми можемо захотіти вивчити розподіл зв'язків для кожного актора. Оскільки відношення, яке ми дивимося, є асиметричним або спрямованим, ми можемо додатково підсумувати надсилання (рядок) та отримання (стовпець) кожного актора. Малюнки 18.3 та 18.4 показують результати Інструменти> Уніваріативна статистика для рядків (tie sending) і стовпців (tie receiving) матриці зв'язку інформації.

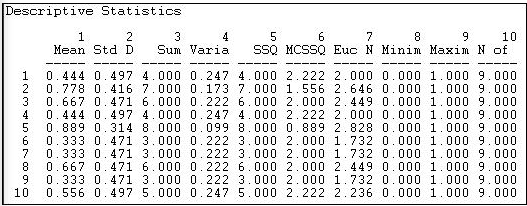
Малюнок 18.3: Уніваріативна описова статистика для рядків інформаційної мережі Knoke

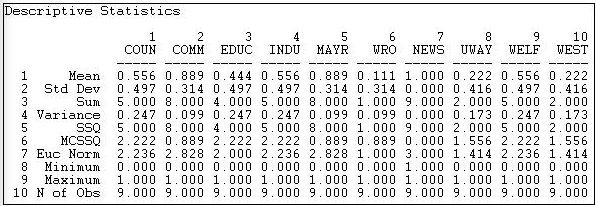
Малюнок 18.4: Уніваріативна описова статистика для стовпців інформаційної мережі Knoke

Ми бачимо, що актор 1 (COUN) має середнє значення (або щільність) зв'язки відправки 0.444. Тобто цей актор надіслав чотири зв'язки наявним дев'яти іншим акторам. Актор 1 отримав дещо більше інформації, ніж надіслали, оскільки середнє значення їх стовпця становить .556. При скануванні стовпця (на малюнку 18.3) або рядка (на малюнку 18.4) засобів, ми зауважимо, що існує досить багато варіативності між акторами - деякі посилають більше і отримують більше інформації, ніж інші.

При цінних даних отримані кошти індексують середню міцність стяжок, а не ймовірність стяжок. При цінних даних міри мінливості можуть бути більш інформативними, ніж з двійковими даними (так як мінливість двійкової змінної є строго функцією її середнього).

Основний момент цього короткого розділу полягає в тому, що коли ми використовуємо статистику для опису мережевих даних, ми описуємо властивості розподілу відносин, або зв'язків. серед акторів — а не властивості розподілу атрибутів між акторами. Основні ідеї центральної тенденції та дисперсії розподілів застосовуються до розподілів реляційних зв'язків точно так само, як і для атрибутивних змінних, але ми описуємо відносини, а не атрибути.

Гіпотези про одне середнє значення або щільність

З різних властивостей розподілу однієї змінної (наприклад, центральна тенденція, дисперсія, перекос), нас зазвичай найбільше цікавить центральна тенденція.

Якщо ми працюємо з розподілом відносин між акторами в мережі, і наша міра сили зв'язки двійкова (нуль/одиниця), середня або центральна тенденція є також пропорція всіх зв'язків, які присутні, і є «щільністю».

Якщо ми працюємо з розподілом відносин між суб'єктами мережі, і оцінюється наша міра сили зав'язування, центральна тенденція зазвичай позначається середня міцність стяжки по всіх відносинам.

Ми можемо перевірити гіпотези про щільність або середню міцність зв'язку мережі. При аналізі змінних це перевірка гіпотези про одновибірковому середньому або пропорції. Ми можемо бути впевнені, що насправді існують зв'язки (нульова гіпотеза: щільність мережі дійсно нульова, і будь-яке відхилення, яке ми спостерігаємо, пов'язано з випадковою варіацією). Ми можемо перевірити гіпотезу про те, що частка наявних бінарних зв'язків відрізняється від 0,50; ми можемо перевірити гіпотезу про те, що середня сила цінного краватки відрізняється від «3».

Мережа>Порівняти щільність>Проти теоретичного параметра виконує статистичний тест для порівняння значення щільності або середньої міцності зв'язку, що спостерігається в мережі, з тестовим значенням.

Припустимо, що я думаю, що всі організації мають тенденцію хотіти безпосередньо поширювати інформацію всім іншим у своїй галузі як спосіб узаконення. самі. Якщо ця теорія вірна, то щільність інформаційної мережі Кноке повинна бути 1,0. Ми бачимо, що це неправда. Але, можливо, різниця між тим, що ми бачимо (щільність = 0,544) і тим, що прогнозує теорія (щільність = 1.000), обумовлена випадковою варіацією (можливо, коли ми збирали інформацію).

Діалогове вікно на малюнку 18.5 налаштовує проблему.

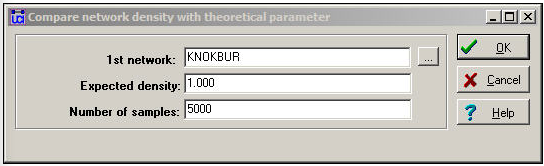
Малюнок 18.5: Діалог порівняння щільності>Проти теоретичного параметра

«Очікувана щільність» - це значення, проти якого ми хочемо протестувати. Тут ми просимо дані переконати нас, що ми можемо бути впевнені у відкиданні ідеї про те, що організації надсилають інформацію всім іншим у своїх галузях.

Параметр «Кількість зразків» використовується для оцінки стандартної похибки для тесту за допомогою «бутстраппінга» або обчислення розрахункової дисперсії вибірки означає, що малює 5000 випадкових підзразків з нашої мережі та побудови розподілу вибірки вимірювань щільності. Розподіл вибірки статистики - це розподіл значень цієї статистики при повторній вибірці. Стандартне відхилення розподілу вибірки статистики (скільки варіацій ми очікуємо побачити від вибірки до вибірки просто випадково) називається стандартною помилкою. На малюнку 18.6 показані результати перевірки гіпотез

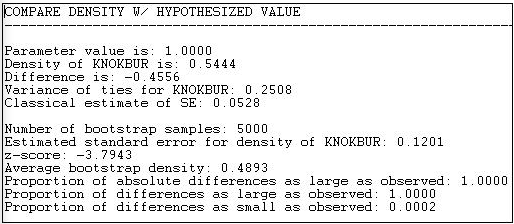
Малюнок 18.6: Результати випробувань

Ми бачимо, що наше тестове значення було 1.000, спостережуване значення - 0.5444, тому різниця між нульовим і спостережуваним значеннями становить -0.4556. Як часто ця велика різниця траплялася б випадковою варіацією вибірки, якби нульова гіпотеза (щільність = 1.000) була дійсно вірною в популяції?

Використання класичної формули для стандартної похибки середнього\(\left( s / \sqrt{N} \right)\) we obtain a sampling variability estimate of 0.0528. If we used this for our test, the test statistic would be -0.4556/0.0528 = 8.6 which would be highly significant as a t-test with N-1 degrees of freedom.

Однак, якщо ми використовуємо метод початкового завантаження побудови 5000 мереж шляхом вибірки випадкових підмножин вузлів кожного разу та обчислюючи щільність кожного разу, середнє значення цей розподіл вибірки виявляється 0,4893, а його стандартне відхилення (або стандартна похибка) виявляється 0,1201.

Використовуючи цю альтернативну стандартну помилку, засновану на випадкових малюнках із спостережуваного зразка, наша тестова статистика становить -3.7943. Цей тест також значущий (р = 0,0002).

Навіщо це робити? Класична формула дає оцінку стандартної помилки (0.0528), яка набагато менше, ніж створена методом bootstrap (0.1201). Це пояснюється тим, що стандартна формула заснована на уявленні про те, що всі спостереження (тобто всі відносини) незалежні. Але, оскільки зв'язки дійсно породжені тими ж 10 акторами, це не є розумним припущенням. Використання фактичних даних про фактичних акторів - зі спостережуваними відмінностями в акторських засобах і дисперсіях, є набагато більш реалістичним наближенням до фактичної варіабельності вибірки, яка відбудеться, якщо, скажімо, нам довелося пропустити Фреда, коли ми збирали дані у вівторок.

Загалом, стандартні формули інференціації для обчислення очікуваної варіабельності вибірки (тобто стандартні помилки) дають нереально малі значення для мережевих даних. Використання їх призводить до найгіршого виду інференційної помилки - хибного позитиву, або відхилення null, коли ми не повинні.