16.3: Рольова алгебра для даних Mulitplex

Last updated
Save as PDF

Page ID: 67381

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустимо, що ми дивилися на єдину матрицю про те, хто з ким дружив. Очевидний спосіб охарактеризувати те, що ми бачимо, - класифікувати кожну пару як «друзів» або «не друзів». Але тепер давайте продовжимо наш аналіз на крок далі (або подивимося на шляхи довжини 2). Тепер кожну пару акторів можна охарактеризувати як друг, а не друг, друг друга, друг недруга, не-друг друга, або не-друг або не-друг. Якщо ми хотіли розглянути шляхи довжиною три... ну, ви отримаєте ідею.

Поняття «рольової алгебри» полягає в розумінні відносин між акторами як реалізацій логічно можливих «сполук» відносин обраних довжин шляхів. Найчастіше в мережевому аналізі ми орієнтуємося на шлях довжини один (два актори пов'язані чи ні). Але, іноді корисно охарактеризувати графік як містить більш складні види відносин (друг друга, не-друг друга і т.д.). Списки цих видів відносин можна отримати, взявши булеві добутки матриць (тобто 0 * 0 = 0, 0* 1 = 0, 1 * 0 = 0, і 1 * 1 = 1). При застосуванні до однієї матриці ми піднімаємо матрицю до степеня (множимо її на себе) і приймаємо булевий добуток; результат генерує матрицю, яка повідомляє нам, чи є зв'язок між кожною парою вузлів, яка має довжину шляху, рівну потужності. Тобто, щоб дізнатися, чи пов'язана кожна пара акторів відношенням «друг друга», беремо булевий твір матриці дружби в квадраті.

Цей (елегантний, але досить загадковий) метод знаходження «складних відносин» може бути застосований до мультиплексних даних як спосіб ідентифікації видів відносин, які існують в мультиплексному графіку. Алгоритм Transform>Semigroup може бути використаний для ідентифікації цих більш складних якісних видів зв'язків між вузлами.

Більшості людей легше зрозуміти це на прикладі, ніж в абстрактному. Тож давайте зробимо дещо розширену експертизу даних Knoke як для інформації, так і для грошових зв'язків.

Якщо розглядати просто прямі відносини, то їх дві: організації можуть бути пов'язані інформацією; організації можуть бути прив'язані грошима. Що робити, якщо розглядати відносини на двох кроках (що називаються «довжиною слів» в рольовій алгебрі)? Крім початкових двох відносин, зараз існує ще чотири:

Коли ми множимо інформаційну матрицю на її транспонування і приймаємо булеві продукти, ми ідентифікуємо зв'язки на кшталт «надсилає інформацію до вузла, який надсилає інформацію...»
Коли ми множимо грошову матрицю на її транспонування і приймаємо булеві продукти, ми визначаємо зв'язок: «відправляє гроші на вузол, який відправляє гроші на...»
Коли ми множимо інформаційну матрицю на грошову матрицю, ми визначаємо зв'язок: «відправляє інформацію до вузла, який відправляє гроші на...»
Коли ми множимо грошову матрицю на інформаційну матрицю, ми визначаємо зв'язок: «відправляє гроші на вузол, який посилає інформацію...»

Ці чотири нові (двоступінчасті) відносини між вузлами є «словами» довжиною два, або «сполуки».

Можна, звичайно, продовжувати з'єднання до ще більшої довжини. У більшості соціологічних аналізів, що мають лише два типи зв'язків, більша довжина рідко є суттєво значущою. Однак з більшою кількістю видів зв'язків кількість типів складних відносин може стати досить великою досить швидко.

Інструмент Трансформувати>Напівгрупа обчислює всі логічно можливі складні типи зв'язків до довжини слова (тобто мережевої відстані), яку вказує користувач. Він виробляє файл журналу, який містить «карту» типів відносин, як ми бачимо на малюнку 16.9. Він також виробляє в окремому файлі матриці суміжності для кожного з типів відносин (рис. 16.10 і 16.11).

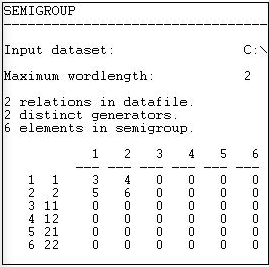
$Ганнеман Скріншот 16-9.png$

Малюнок 16.9: Напівгрупи довжини слова 2 для інформаційно-грошових мереж Кноке

Вихід говорить нам про те, що було два відносини (інформаційний і грошовий). Це були «генератори», які використовувалися для створення типів. Шість можливих складних відносин були створені для довжини слова 2 (ідентифіковані вниз лівою стороною). Відносини 1 і 2 - це інформація і гроші окремо - вихідні матриці. Відношення 3 - це з'єднання інформації з собою; відношення чотири - це з'єднання інформації з грошима тощо Числа (3, 4, 5, 6) - це просто керівництва до якої матриці у вихідному файлі відноситься до якого відношення.

З цих нових «типів» відносин (які є сполуками всередині та між двома типами зв'язків) ми можемо генерувати нові матриці суміжності, які показують, які пари акторів з'єднані кожним конкретним типом відносин. Вони представлені у вигляді ряду матриць суміжності, як показано на малюнку 16.10 і продовжено на малюнку 16.11.

$Ганнеман Скріншот 16-10.png$

Малюнок 16.10: Таблиці відносин для малюнка 16.9 (частина 1)

Матриця 1 - це просто вихідна інформаційна матриця; матриця 2 - вихідна грошова матриця. Матриця 3 - це з'єднання інформації з інформацією - які актори пов'язані відносинами «Его посилає інформацію тому, хто надсилає інформацію Альтеру»?

$Ганнеман Скріншот 16-11.png$

Малюнок 16.11: Таблиці відносин для малюнка 16.9 (частина 2)

Матриця 4 - це з'єднання грошей з собою, або «Его посилає гроші тому, хто надсилає гроші Альтеру».

Матриці 5 і 6 є, в деякому роді, найцікавішими. Хоча обмін інформацією для інформації та гроші за гроші є очевидними способами інтеграції мережі, можливо також, що суб'єкти можуть бути інтегровані відносинами, які включають як «яблука», так і «апельсини». Тобто я можу надсилати гроші та отримувати інформацію; я можу надсилати інформацію та отримувати гроші.

Рольова алгебра виявилася особливою цінністю при вивченні родинних відносин, де міжпоколінні (батьківські/дочірні) зв'язки записуються в одній матриці, а відносини всередині покоління записуються в іншій. Різні сполуки (наприклад, «дитина дитини», «дитина брата») досить легко захоплюють значущі терміни в родинних стосунках.