14.3: Пошук наборів еквівалентності

При двійкових даних числові алгоритми використовуються для пошуку класів акторів, що задовольняють математичним визначенням автоморфної еквівалентності. В основному, вузли графіка обмінюються, а відстані між усіма парами акторів на новому графіку порівнюються з вихідним графіком. Коли новий графік і старий граф мають однакові відстані між вузлами, графіки ізоморфні, а «обмін», який був зроблений, ідентифікує ізоморфні підграфи.

Один підхід до двійкових даних, «всі перестановки», ( Мережа>Ролі та посади>Автоморфічні>Усі перестановки ) буквально порівнює всі можливі заміни вузлів, щоб знайти ізоморфні графіки. При навіть невеликому графіку існує дуже велика кількість таких альтернатив, а обчислення великі. Альтернативний підхід з тим же наміром («оптимізація за допомогою пошуку табу») (Мережа>Ролі та позиції> Точні> Оптимізація ) може набагато швидше сортувати вузли в визначену користувачем кількість розділів таким чином, щоб максимізувати автоморфну еквівалентність. Однак немає ніякої гарантії, що кількість вибраних розділів (класів еквівалентності) є «правильною», або що виявлені автоморфізми є «точними». Для більших наборів даних, і там, де ми готові розважити ідею, що дві підструктури можуть бути «майже» еквівалентними, оптимізація є дуже корисним методом.

Коли ми маємо міри міцності, вартості або ймовірності відносин між вузлами (тобто цінні дані), точна автоморфна еквівалентність набагато рідше. Однак можна визначити класи приблизно рівнозначних акторів на основі їх профілю відстані до всіх інших суб'єктів. Метод «еквівалентності відстаней» (Мережа>Ролі та позиції>Автоморфічна>MaxSIM ) виробляє заходи ступеня автоморфної еквівалентності для кожної пари вузлів, які можуть бути досліджені шляхом кластеризації та методи масштабування для виявлення наближених класів. Цей метод також може бути застосований до двійкових даних, спочатку перетворивши двійкову суміжність у деяку міру відстані графіка (зазвичай, геодезичну відстань).

Давайте розглянемо їх трохи докладніше, з деякими прикладами.

Усі перестановки (тобто груба сила)

Автоморфізми на графіку можуть бути ідентифіковані методом грубої сили дослідження всіх можливих перестановок графа. З невеликим графіком і швидким комп'ютером, це корисна річ, щоб зробити. В основному, кожна можлива перестановка графіка розглядається, щоб побачити, чи має він ту саму структуру зв'язки, що і вихідний графік. Для графіків більш ніж декількох акторів кількість перестановок, які потрібно порівняти, стає надзвичайно великою.

Давайте скористаємося Мережі>Ролі та посади>Автоморфічні>Усі перестановки для пошуку мережі Вассермана-Фауста, показаної на малюнку 14.1.

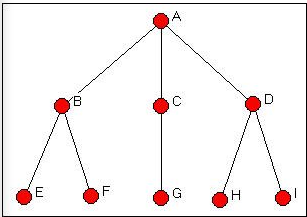
Малюнок 14.1: Мережа Вассермана-Фауста

Підсумки Мережі>Ролі та посади>Автоморфічні>Усі перестановки для цього графіка показані на малюнку 14.2.

Малюнок 14.2: Автоморфні еквіваленти за всіма перестановками для мережі Вассермана-Фауста

Алгоритм розглянув понад трьохсот шістдесят дві тисячі можливих перестановок графа. Класи ізоморфізму, які він розташований, називаються «орбітами». І, результати відповідають нашому логічному аналізу (глава 12). Існує п'ять «типів» акторів, які вбудовані на рівних відстанях від інших наборів акторів: актор А (орбіта 1), актор С (орбіта 3), і актор G (орбіта 7) унікальні. Актори B і D утворюють клас акторів, якими можна обмінюватися, якщо також обмінюються членами інших класів; актори E, F, H і I (5, 6, 8 і 9) також утворюють клас обмінних акторів.

Відзначимо, що класи автоморфізму ідентифікують групи акторів, які мають однакову схему віддаленості від інших акторів, а не самі «підструктури» (в цьому випадок, дві гілки дерева.

Оптимізація за допомогою пошуку Tabu

Для великих графіків прямий пошук всіх еквівалентів недоцільний як тому, що він обчислювально-інтенсивний, так і тому, що точно еквівалентні актори, ймовірно, будуть рідкісними.

Мережа>Ролі та позиції>Точна>Оптимізація надає числовий інструмент для пошуку найкращих наближень до обраної користувачем кількості класів автоморфізму. Використовуючи цей метод, важливо вивчити діапазон можливих чисел розділів (якщо немає попередньої теорії про це), щоб визначити, скільки розділів є корисними. Вибравши ряд розділів, корисно кілька разів повторно запустити алгоритм, щоб застрахувати, що був знайдений глобальний, а не локальний мінімум.

Метод починається з випадкового розподілу вузлів на розділи. Міра поганості придатності будується шляхом обчислення сум квадратів для кожного рядка та кожного стовпця всередині кожного блоку та обчислення дисперсії цих сум квадратів. Потім ці відхилення підсумовуються по блоках для побудови міри поганості придатності. Пошук продовжує знаходити розподіл акторів на розділи, що мінімізує цю погану статистику придатності.

Те, що мінімізується, - це функція несхожості дисперсії балів всередині розділів. Тобто алгоритм прагне згрупувати акторів, які мають подібні кількості мінливості у своїх рядках та стовпцях балів у блоках. Актори, які мають подібну мінливість, ймовірно, мають подібні профілі зв'язків, надісланих та отриманих всередині та через блоки - хоча вони не обов'язково мають однакові зв'язки з тими ж іншими акторами, вони, ймовірно, матимуть зв'язки однакової відстані з акторами інших класів.

Давайте ще раз розберемо мережу обміну інформацією бюрократії Кноке, цього разу шукаючи автоморфізми. У інформаційних даних Кноке немає точних автоморфізмів. Це насправді не дивно, враховуючи складність візерунка (і особливо, якщо відрізняти в-краватки від out-ties) з'єднань.

Ми запустили процедуру кілька разів, запитуючи розділи на різну кількість класів. Малюнок 14.3 підсумовує «погану посадку» моделей.

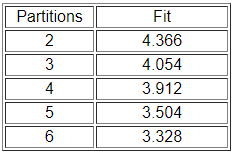
Рисунок 14.3: Пристосування моделей автоморфної еквівалентності до інформаційної мережі Кноке

Немає «правильної» відповіді про те, скільки класів є. Є дві тривіальні відповіді: ті, які групують всі випадки разом в один розділ, і ті, які розділяють кожен випадок на власний розділ. У перервах між ними можна слідувати логіці графіка «скріну» з факторного аналізу, щоб вибрати значущу кількість розділів. Подивіться спочатку результати для трьох розділів (рис. 14.4).

Малюнок 14.4: Розв'язок автоморфної еквівалентності 3 класу для інформаційної мережі Кноке

На цьому рівні приблизної еквівалентності виділяють три класи - дві особини і одна велика група. Газета (актор 7) має низькі темпи відправки (рядок) і високі показники прийому (графа); мер (актор 5) має високі показники відправки і високі показники прийому. Маючи лише три класи, решта акторів групуються в приблизний клас з приблизно рівною (і вищою) мінливістю як відправки, так і прийому.

Оскільки автоморфна еквівалентність фактично діє на профіль відстаней акторів, вона має тенденцію ідентифікувати групи акторів, які мають подібні закономірності в'їзду та виходу ступінь. Це виходить за рамки структурної еквівалентності (яка підкреслює зв'язки з точно такими ж іншими акторами) до більш загальної та нечіткої ідеї про те, що два актори еквівалентні, якщо вони аналогічно вбудовані. Акцент зміщується від індивідуальної позиції, до ролі позиції в структурі всього графіка.

Еквівалентність відстаней (MaxSIM)

Коли ми маємо інформацію про силу, вартість або ймовірність відносин (тобто цінні дані), точна автоморфна еквівалентність може бути надзвичайно рідкісною. Але, оскільки автоморфна еквівалентність підкреслює схожість у профілі відстаней акторів від інших, ідея приблизної еквівалентності може бути застосована до цінних даних. Мережа>Ролі і посади>Автоморфічна>MaxSIM генерує матрицю «подібності» між формою розподілів зв'язків акторів, які можуть бути згруповані шляхом кластеризації та масштабування в наближені класи. Підхід також може бути застосований до двійкових даних, якщо спочатку перетворити матрицю суміжності в матрицю геодезичних ближніх зв'язків (яку можна розглядати як цінну міру міцності зв'язків).

Алгоритм починається з (зворотної) відстані або міцності матриці стяжки. Відстані кожного актора переорганізовані в відсортований список від низького до високого, а евклідова відстань використовується для обчислення несхожості між профілями відстаней кожної пари акторів. Алгоритм оцінює акторів, які мають подібні профілі відстані, як більш автоморфічно еквівалентні. Знову ж таки, основна увага приділяється тому, чи актор у має подібний набір відстаней, незалежно від того, які відстані, до актора v. Знову ж таки, розмірне масштабування або кластеризація відстаней можуть бути використані для ідентифікації наборів приблизно автоморфічно еквівалентних акторів.

Давайте застосуємо цю ідею до двох прикладів, одному простому і абстрактному, іншому більш реалістичному. Для початку розглянемо «лінійну» мережу (рис. 14.5).

Малюнок 14.5: Лінійна мережа

На малюнку 14.6 показані результати аналізу цієї мережі за допомогою Мережа>Ролі та посади>Автоморфічна>MaxSIM.

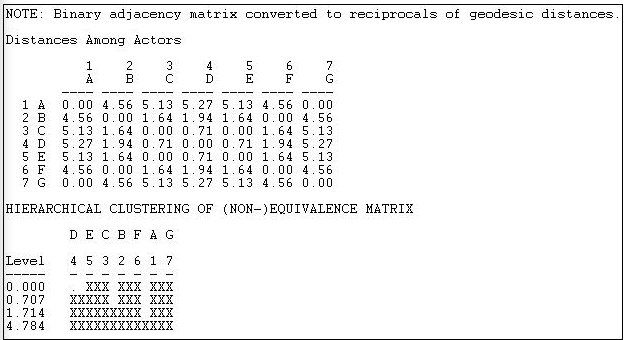
Малюнок 14.6: Автоморфна еквівалентність геодезичних відстаней в лінійній мережі

Насамперед необхідно перетворити матрицю суміжності в геодезичну матрицю відстані. Потім береться зворотна відстань, і створюється вектор записів рядків, об'єднаних із записами стовпців для кожного актора. Евклідові відстані між цими списками потім створюються як міра неавтоморфної еквівалентності, і застосовується ієрархічна кластеризація.

Ми бачимо, що актори 3 і 5 (С і Е) утворюють клас; актори 2 і 6 (В і Ф) утворюють клас; актори 1 і 7 (А і Г) утворюють клас, а актор 4 (D) - клас. Математично це розумний результат; обмін мітками акторів всередині цих наборів може відбуватися і все ще виробляти ізоморфну матрицю відстані. Результат також має суттєвий сенс - і цілком подібний до мережі Wasserman-Faust.

Цей метод наближення також може бути застосований там, де дані оцінюються. Якщо ми подивимось на наші дані про донорів політичних кампаній у Каліфорнії, ми маємо заходи міцності зв'язків між суб'єктами, які є кількістю спільних позицій у кампаніях, які вони мають, коли вони сприяли. На малюнку 14.7 показана частина вихідних даних Мережа>Ролі та позиції>Автоморфічна>MaxSIM .

Малюнок 14.7: Приблизна автоморфна еквівалентність політичних донорів Каліфорнії (усічена)

Ця невелика частина великої частини продукції (в мережі є 100 донорів) показує, що ряд неіндійських казино і гоночних треків кластера разом, і окремо від деяких інших донорів, які в першу чергу займаються питаннями освіти та екології.

Ідентифікація приблизних класів еквівалентності в цінних даних може бути корисною при знаходженні груп суб'єктів, які мають подібне розташування в структурі графік в цілому. Однак, підкреслюючи профілі відстані, можна знайти класи акторів, які включають вузли, які досить віддалені один від одного, але на подібній відстані до всіх інших акторів. Тобто актори, які мають схожі позиції в мережі в цілому.