7.4: Ортогональність

Ортогональна діагоналізація

Починаємо цей розділ з згадки деяких важливих визначень. Нагадаємо з визначення 4.11.4, що ненульові вектори називаються ортогональними, якщо їх точковий добуток дорівнює$0$. Множина є ортонормальною, якщо вона ортогональна, і кожен вектор є одиничним вектором.

Ортогональна матриця$U$, з визначення 4.11.7, є такою, в якій$UU^{T} = I$. Іншими словами, транспонування ортогональної матриці дорівнює її зворотному. Ключовою характеристикою ортогональних матриць, яка буде суттєвою в цьому розділі, є те, що стовпці ортогональної матриці утворюють ортонормальну множину.

Тепер нагадаємо ще одне важливе визначення.

Визначення$\PageIndex{1}$: Symmetric and Skew Symmetric Matrices

Реальна$n\times n$$A,$ матриця симетрична,$A^{T}=A.$ якщо$A=-A^{T},$ тоді$A$ називається косою симетричною.

Перш ніж довести істотну теорему, ми спочатку вивчимо наступну лему, яка буде використана нижче.

Лемма$\PageIndex{1}$: The Dot Product

$A=\left ( a_{ij} \right )$Дозволяти реальна симетрична$n \times n$ матриця, і нехай$\vec{x}, \vec{y} \in \mathbb{R}^n$. Тоді $$A\vec{x} \cdot \vec{y} = \vec{x} \cdot A \vec{y}\nonumber$$

Доказ

Цей результат випливає з визначення крапкового добутку разом із властивостями множення матриць наступним чином: $$\begin{aligned} A\vec{x} \cdot \vec{y} &= \sum_{k,l}a_{kl}x_{l}y_{k} \\ &=\sum_{k,l} (a_{lk})^Tx_{l}y_{k} \\ &= \vec{x}\cdot A^{T}\vec{y} \\ &= \vec{x}\cdot A \vec{y}\end{aligned}$$

Останній крок випливає з$A^T = A$, так як$A$ є симетричним.

Тепер ми можемо довести, що власні значення дійсної симетричної матриці є дійсними числами. Розглянемо наступну важливу теорему.

Теорема$\PageIndex{1}$: Orthogonal Eigenvectors

$A$Дозволяти бути справжньою симетричною матрицею. Тоді власні значення$A$ є дійсними числами, а власні вектори, що відповідають різним власним значенням, є ортогональними.

Доказ

Нагадаємо, що для комплексного числа$a+ib,$ складний сполучений, позначений значенням$\overline{a+ib}$ задається$\overline{a+ib}=a-ib.$ позначенням,$\overline{\vec{x}}$ буде позначати вектор, який має кожен запис замінений своїм складним сполученим.

Припустимо,$A$ це реальна симетрична матриця і$A\vec{x}=\lambda \vec{x}$. Потім $$\overline{\lambda \vec{x}}^{T}\vec{x}=\left( \overline{A \vec{x}}\right) ^{T}\vec{x}=\overline{\vec{x}}^{T}A^{T}\vec{x}= \overline{\vec{x}}^{T}A\vec{x}=\lambda \overline{\vec{x}}^{T} \vec{x}\nonumber$$ поділ$\overline{\vec{x}}^{T}\vec{x}$ на обидві сторони дає$\overline{\lambda }=\lambda$, що говорить,$\lambda$ що реально. Для цього нам потрібно переконатися в цьому$\overline{\vec{x}}^{T}\vec{x} \neq 0$. Зверніть увагу, що$\overline{\vec{x}}^{T}\vec{x} = 0$ якщо і тільки якщо$\vec{x} = \vec{0}$. Оскільки ми вибрали$\vec{x}$ таке$A\vec{x} = \lambda \vec{x}$, що,$\vec{x}$ є власнимвектором і тому повинен бути ненульовим.

Тепер припустимо$A$, що реально симетрично і$A\vec{x}=\lambda \vec{x}$,$A \vec{y}=\mu \vec{y}$ де$\mu \neq \lambda$. Тоді, оскільки$A$ є симетричним, з Лемми випливає$\PageIndex{1}$ про точковий добуток, що $$\lambda \vec{x}\cdot \vec{y}=A\vec{x}\cdot \vec{y}=\vec{x}\cdot A\vec{y}=\vec{x}\cdot \mu \vec{y}=\mu \vec{x}\cdot \vec{y}\nonumber$$ Звідси$\left( \lambda -\mu \right) \vec{x}\cdot \vec{y}=0.$ випливає, що, оскільки$\lambda -\mu \neq 0,$ це повинно бути таким$\vec{x}\cdot \vec{y}=0$. Тому власні вектори утворюють ортогональну множину.

Подібним чином доведена наступна теорема.

Теорема$\PageIndex{2}$: Eigenvalues of Skew Symmetric Matrix

Власні значення дійсної симетричної матриці з нахилом або дорівнюють чистим уявним числам,$0$ або є чистими уявними числами.

Доказ

По-перше, зверніть увагу,$A=0$ що якщо нульова матриця, то$A$ є косою симетричною і має власні значення, рівні$0$.

Припустимо$A$,$A=-A^{T}$ що так перекіс симетричний і$A\vec{x}=\lambda \vec{x}$. Тоді $$\overline{\lambda \vec{x}}^{T}\vec{x}=\left( \overline{A \vec{x}}\right) ^{T}\vec{x}=\overline{\vec{x}}^{T}A^{T}\vec{x}=- \overline{\vec{x}}^{T}A\vec{x}=-\lambda \overline{\vec{x}}^{T} \vec{x}\nonumber$$ і так, розділяючи на,$\overline{\vec{x}}^{T}\vec{x}$ як раніше,$\overline{\lambda }=-\lambda .$ Дозволити$\lambda =a+ib,$ це означає$a-ib=-a-ib$ і так$a=0.$ Таким чином чисто$\lambda$ уявне.

Розглянемо наступний приклад.

Приклад$\PageIndex{1}$: Eigenvalues of a Skew Symmetric Matrix

Дозвольте$A=\left[ \begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array} \right] .$ знайти свої власні значення.

Рішення

Спочатку зверніть увагу,$A$ що перекіс симетричний. За теоремою власні значення будуть або дорівнювати$\PageIndex{2}$,$0$ або бути чистими уявними. Власні значення$A$ отримують шляхом розв'язання звичайного рівняння $$\det (\lambda I - A ) = \det \left[ \begin{array}{rr} \lambda & 1 \\ -1 & \lambda \end{array} \right] =\lambda ^{2}+1=0\nonumber$$

Звідси власні значення є$\pm i,$ чистими уявними.

Розглянемо наступний приклад.

Приклад$\PageIndex{2}$: Eigenvalues of a Symmetric Matrix

Дозвольте$A=\left[ \begin{array}{rr} 1 & 2 \\ 2 & 3 \end{array} \right] .$ знайти свої власні значення.

Рішення

По-перше, зверніть увагу, що$A$ це симетрично. За теоремою$\PageIndex{1}$, всі власні значення будуть дійсними. Власні значення$A$ отримують шляхом розв'язання звичайного $$\det (\lambda I - A) = \det \left[ \begin{array}{rr} \lambda - 1 & -2 \\ -2 & \lambda - 3 \end{array} \right] = \lambda^2 -4\lambda -1=0\nonumber$$ рівняння. Власні значення задаються$\lambda_1 =2+ \sqrt{5}$ і$\lambda_2 =2-\sqrt{5}$ які обидва є дійсними.

Нагадаємо, що діагональна матриця$D=\left ( d_{ij} \right )$ - це та, в якій$d_{ij} = 0$ коли завгодно$i \neq j$. Іншими словами, всі числа не на головній діагоналі рівні нулю.

Розглянемо наступну важливу теорему.

Теорема$\PageIndex{3}$: Orthogonal Diagonalization

$A$Дозволяти бути справжньою симетричною матрицею. Тоді існує ортогональна матриця$U$ така, що $$U^{T}AU = D\nonumber$$ де$D$ діагональна матриця. Крім того,$D$ діагональні записи є власними значеннями$A$.

Ми можемо використовувати цю теорему для діагоналізації симетричної матриці, використовуючи ортогональні матриці. Розглянемо наступний наслідок.

Слідство$\PageIndex{1}$: Orthonormal Set of Eigenvectors

Якщо$A$ дійсна$n\times n$ симетрична матриця, то існує ортонормальна множина власних векторів,$\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\} .$

Доказ

Оскільки$A$ є симетричним, то за теоремою існує ортогональна матриця$U$ така$\PageIndex{3}$, що$U^{T}AU=D,$ діагональна матриця, діагональні записи якої є власними значеннями$A.$ Тому, оскільки$A$ симетрична і всі матриці дійсні, $$\overline{D}=\overline{D^{T}}=\overline{U^{T}A^{T}U}=U^{T}A^{T}U=U^{T}AU=D\nonumber$$ показуючи $D$є реальним, тому що кожен запис$D$ дорівнює його складному сполученню.

Тепер нехай $$U=\left[ \begin{array}{cccc} \vec{u}_{1} & \vec{u}_{2} & \cdots & \vec{u}_{n} \end{array} \right]\nonumber$$ де$\vec{u}_{i}$ позначають стовпці$U$ і $$D=\left[ \begin{array}{ccc} \lambda _{1} & & 0 \\ & \ddots & \\ 0 & & \lambda _{n} \end{array} \right]\nonumber$$ Рівняння,$U^{T}AU=D$ має на увазі$AU = UD$ і $$\begin{aligned} AU &=\left[ \begin{array}{cccc} A\vec{u}_{1} & A\vec{u}_{2} & \cdots & A\vec{u}_{n} \end{array} \right] \\ &=\left[ \begin{array}{cccc} \lambda _{1}\vec{u}_{1} & \lambda _{2}\vec{u}_{2} & \cdots & \lambda _{n}\vec{u}_{n} \end{array} \right] \\ &= UD\end{aligned}$$ де записи позначають стовпці$AU$ і$UD$ відповідно. Тому,$A\vec{u}_{i}=\lambda _{i}\vec{u}_{i}$. Оскільки$U$ матриця ортогональна,$ij^{th}$ запис$U^{T}U$ дорівнює$\delta _{ij}$ і тому $$\delta _{ij}=\vec{u}_{i}^{T}\vec{u}_{j}=\vec{u}_{i}\cdot \vec{u} _{j}\nonumber$$ Це доводить наслідок, оскільки він показує, що вектори$\left\{ \vec{u} _{i}\right\}$ утворюють ортонормальну множину.

Визначення$\PageIndex{2}$: Principal Axes

$A$Дозволяти бути$n \times n$ матрицею. Тоді головні осі$A$ є сукупністю ортонормальних власних векторів$A$.

У наступному прикладі ми розглянемо, як знайти таку сукупність ортонормальних власних векторів.

Приклад$\PageIndex{3}$: Find an Orthonormal Set of Eigenvectors

Знайти ортонормальну множину власних векторів для симетричної матриці $$A = \left[ \begin{array}{rrr} 17 & -2 & -2 \\ -2 & 6 & 4 \\ -2 & 4 & 6 \end{array} \right]\nonumber$$

Рішення

Нагадаємо, Порядок 7.1.1 для знаходження власних значень та власних векторів матриці. Ви можете переконатися, що власні значення є$18,9,2.$ Спочатку знайти власний вектор для,$18$ вирішивши рівняння$(18I-A)X = 0$. Відповідну доповнену матрицю задають $$\left[ \begin{array}{ccc|c} 18-17 & 2 & 2 & 0 \\ 2 & 18-6 & -4 & 0 \\ 2 & -4 & 18-6 & 0 \end{array} \right]\nonumber$$ Зведена форма рядка-ешелону $$\left[ \begin{array}{rrr|r} 1 & 0 & 4 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ Отже, власний вектор - $$\left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right]\nonumber$$ Далі знайдіть власний вектор для$\lambda =9.$ Розширеної матриці, а результуюча зменшена форма рядка-ешелону є $$\left[ \begin{array}{ccc|c} 9-17 & 2 & 2 & 0 \\ 2 & 9-6 & -4 & 0 \\ 2 & -4 & 9-6 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & - \frac{1}{2} & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ Таким чином, власний вектор для$\lambda =9$ $$\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right]\nonumber$$ Нарешті, знайдіть власний вектор для$\lambda =2.$ відповідної розширеної матриці та зменшеної форми рядка-ешелону $$\left[ \begin{array}{ccc|c} 2-17 & 2 & 2 & 0 \\ 2 & 2-6 & -4 & 0 \\ 2 & -4 & 2-6 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ Таким чином, власний вектор$\lambda =2$ для $$\left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right]\nonumber$$

Набір власних векторів для$A$ задається $$\left\{ \left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right], \left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right], \left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right] \right\}\nonumber$$ Ви можете переконатися, що ці власні вектори утворюють ортогональну множину. Діливши кожен власний вектор на його величину, отримаємо ортонормальний множина: $$\left\{ \frac{1}{\sqrt{18}}\left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right] ,\frac{1}{3}\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right] ,\frac{1}{\sqrt{2}}\left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right] \right\}\nonumber$$

Розглянемо наступний приклад.

Приклад$\PageIndex{4}$: Repeated Eigenvalues

Знайти ортонормальну множину з трьох власних векторів для матриці $$A = \left[ \begin{array}{rrr} 10 & 2 & 2 \\ 2 & 13 & 4 \\ 2 & 4 & 13 \end{array} \right]\nonumber$$

Рішення

Ви можете перевірити, що власні значення$A$ є$9$ (з кратністю два) і$18$ (з кратністю один). Розглянемо власні вектори, відповідні$\lambda =9$. Відповідна розширена матриця і зменшена форма рядка-ешелону задаються $$\left[ \begin{array}{ccc|c} 9-10 & -2 & -2 & 0 \\ -2 & 9-13 & -4 & 0 \\ -2 & -4 & 9-13 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 2 & 2 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ і тому власні вектори мають форму $$\left[ \begin{array}{c} -2y-2z \\ y \\ z \end{array} \right]\nonumber$$ Нам потрібно знайти два з них, які є ортогональними. Нехай один буде дано установкою$z=0$ і$y=1$, даючи$\left[ \begin{array}{r} -2 \\ 1 \\ 0 \end{array} \right]$.

Для того, щоб знайти власний вектор, ортогональний цьому, нам потрібно задовольнити значення $$\left[ \begin{array}{r} -2 \\ 1 \\ 0 \end{array} \right] \cdot \left[ \begin{array}{c} -2y-2z \\ y \\ z \end{array} \right] =5y+4z=0\nonumber$$ The$y=-4$ і$z=5$ задовольнити це рівняння, давши інший власний вектор, відповідний$\lambda=9$ як $$\left[ \begin{array}{c} -2\left( -4\right) -2\left( 5\right) \\ \left( -4\right) \\ 5 \end{array} \right] =\left[ \begin{array}{r} -2 \\ -4 \\ 5 \end{array} \right]\nonumber$$ Next, знайти власний вектор для$\lambda =18.$ Розширена матриця і результуючий приведений рядок- форма ешелону задається $$\left[ \begin{array}{ccc|c} 18-10 & -2 & -2 & 0 \\ -2 & 18-13 & -4 & 0 \\ -2 & -4 & 18-13 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & - \frac{1}{2} & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ і тому власним вектором є $$\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right]\nonumber$$

Розділивши кожен власний вектор на його довжину, ортонормальна множина дорівнює $$\left\{ \frac{1}{\sqrt{5}} \left[ \begin{array}{r} -2\\ 1 \\ 0 \end{array} \right] , \frac{\sqrt{5}}{15} \left[ \begin{array}{r} -2 \\ -4 \\ 5 \end{array} \right] , \frac{1}{3}\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right] \right\}\nonumber$$

У вищезгаданому рішенні повторне власне значення означає, що було б багато інших ортонормальних основ, які могли б бути отримані. Хоча ми вирішили взяти$z=0, y=1$, ми могли б так само легко взяти$y=0$ або навіть$y=z=1.$ Будь-яка така зміна призвела б до іншого ортонормального набору.

Згадаймо наступне визначення.

Визначення$\PageIndex{3}$: Diagonalizable

$n\times n$$A$Матриця, як кажуть, не дефектна або діагональна, якщо існує оборотна матриця$P$ така, що$P^{-1}AP=D$ де$D$ діагональна матриця.

Як зазначено в теоремі$\PageIndex{3}$ if$A$ є дійсною симетричною матрицею, існує ортогональна матриця$U$ така, що$U^{T}AU=D$ де$D$ діагональна матриця. Тому кожна симетрична матриця є діагональною, оскільки якщо$U$ це ортогональна матриця, вона є інвертованою, а її зворотною є$U^{T}$. У цьому випадку ми говоримо,$A$ що ортогонально діагонально. Тому кожна симетрична матриця насправді ортогонально діагонально піддається діагоналі. Наступна теорема надає ще один спосіб визначити, чи є матриця ортогонально діагонально діагональною.

Теорема$\PageIndex{4}$: Orthogonally Diagonalizable

$A$Дозволяти бути$n \times n$ матрицею. Потім$A$ ортогонально діагонально можна діагонально, якщо і тільки якщо$A$ має ортонормальний набір власних векторів.

Нагадаємо з Слідство$\PageIndex{1}$, що кожна симетрична матриця має ортонормальний набір власних векторів. Насправді ці три умови рівнозначні.

У наступному прикладі$U$ буде знайдено ортогональну матрицю для ортогональної діагональної діагоналі матриці.

Приклад$\PageIndex{5}$: Diagonalize a Symmetric Matrix

Дозвольте$A=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right] .$ знайти ортогональну матрицю$U$ таку, яка$U^{T}AU$ є діагональною матрицею.

Рішення

У цьому випадку власні значення є$2$ (з кратністю один) і$1$ (з кратністю два). Спочатку знайдемо власний вектор для власного значення$2$. Відповідна доповнена матриця і результуюча зменшена форма рядка-ешелону задаються $$\left[ \begin{array}{ccc|c} 2-1 & 0 & 0 & 0 \\ 0 & 2- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 2- \frac{3}{2} & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ і таким чином власний вектор є $$\left[ \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right]\nonumber$$ Однак бажано, щоб власні вектори були одиничними векторами і таким чином ділення цього вектора на його довжину дає $$\left[ \begin{array}{c} 0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right]\nonumber$$ Далі знайти власні вектори, відповідні власному значенню. дорівнює$1$. Відповідна розширена матриця і результуюча зменшена форма рядка-ешелону задаються: $$\left[ \begin{array}{ccc|c} 1-1 & 0 & 0 & 0 \\ 0 & 1- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 1- \frac{3}{2} & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber$$ Отже, власні вектори мають вигляд $$\left[ \begin{array}{r} s \\ -t \\ t \end{array} \right]\nonumber$$ Два з них, які є ортонормальними є$\left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right]$, вибираючи$s=1$ і$t=0$, і$\left[ \begin{array}{c} 0 \\ - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right]$, дозволяючи$s=0$,$t= 1$ і нормалізація результуючого вектора.

Щоб отримати бажану ортогональну матрицю, ми дозволимо ортонормальним власним векторам, обчисленим вище, стовпцями. $$\left[ \begin{array}{rrr} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right]\nonumber$$

Для перевірки обчислюють$U^{T}AU$ наступним чином: бажану $$U^{T}AU = \left[ \begin{array}{rrr} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right] \left[ \begin{array}{rrr} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right]\nonumber$$ $$=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right] = D\nonumber$$ діагональну матрицю. Зверніть увагу, що власні вектори, які будують стовпці$U$, знаходяться в тому ж порядку, що і власні значення в$D$.

Закінчуємо цей розділ теоремою, яка узагальнює більш ранні результати.

Теорема$\PageIndex{5}$: Triangulation of a Matrix

$A$Дозволяти бути$n \times n$ матрицею. Якщо$A$ має$n$ дійсні власні значення, то ортогональна матриця$U$ може бути знайдена для отримання верхньої трикутної матриці$U^T A U$.

тріангуляція

Ця теорема дає корисний наслідок.

Слідство$\PageIndex{2}$: Determinant and Trace

$A$Дозволяти$n \times n$ матриця з власними значеннями$\lambda_1, \cdots, \lambda_n$. Потім випливає, що$\det(A)$ дорівнює добутку на$\lambda_i$, при цьому$trace(A)$ дорівнює сумі$\lambda_i$.

Доказ

За теоремою$\PageIndex{5}$ існує ортогональна матриця$U$ така$U^TAU=P$, що, де$P$ знаходиться верхня трикутна матриця. Так$P$ як схожий на$A$, власні значення$P$ є$\lambda_1, \lambda_2, \ldots, \lambda_n$. Крім того,$P$ оскільки (верхня) трикутна, записи на головній діагоналі$P$ є його власними значеннями, так$\det(P)=\lambda_1 \lambda_2 \cdots \lambda_n$ і$trace(P)=\lambda_1 + \lambda_2 + \cdots + \lambda_n$. Так як$P$ і$A$ схожі,$\det(A)=\det(P)$ і$trace(A)=trace(P)$, тому і результати слідують.

Декомпозиція сингулярних значень

Починаємо цей розділ з важливого визначення.

Визначення$\PageIndex{4}$: Singular Values

$A$Дозволяти бути$m\times n$ матрицею. Особливими значеннями$A$ є квадратні корені позитивних власних значень$A^TA.$

Декомпозиція сингулярних значень (SVD) може розглядатися як узагальнення ортогональної діагоналізації симетричної матриці до довільної$m\times n$ матриці. Це розкладання знаходиться в центрі уваги цього розділу.

Нижче наведено корисний результат, який допоможе при обчисленні SVD матриць.

Пропозиція$\PageIndex{1}$: Same Nonzero Eigenvalues

$A$Дозволяти бути$m \times n$ матрицею. Тоді$A^TA$ і$AA^T$ мають однакові ненульові власні значення.

Доказ

Припустимо,$A$ це$m\times n$ матриця, і припустимо, що$\lambda$ це ненульове власне значення$A^TA$. Тоді існує ненульовий вектор$X\in \mathbb{R}^n$ такий, що $$\label{nonzero} (A^TA)X=\lambda X.$$

Множення обох сторін цього рівняння на$A$ виходи: $$\begin{aligned} A(A^TA)X & = A\lambda X\\ (AA^T)(AX) & = \lambda (AX).\end{aligned}$$ Оскільки$\lambda\neq 0$ і$X\neq 0_n$, і$\lambda X\neq 0_n$, отже, на рівняння$\eqref{nonzero}$,$(A^TA)X\neq 0_m$; таким чином$A^T(AX)\neq 0_m$, маючи на увазі це$AX\neq 0_m$.

Тому$AX$ є власним вектором,$AA^T$ відповідним власному значенню$\lambda$. Аналогічний аргумент може бути використаний, щоб показати, що кожне ненульове власне значення$AA^T$ є власним значенням$A^TA$, таким чином завершуючи доказ.

З огляду на$m\times n$ матрицю$A$, ми побачимо, як висловити$A$ як продукт $$A=U\Sigma V^T\nonumber$$ , де

• $U$$m\times m$ортогональна матриця, стовпці якої є власними векторами$AA^T$.
• $V$$n\times n$ортогональна матриця, стовпці якої є власними векторами$A^TA$.
• $\Sigma$$m\times n$матриця, чиї тільки ненульові значення лежать на її головній діагоналі, і є сингулярними значеннями$A$.

Як же знайти таке розкладання? Ми ставимо за мету розкласти$A$ в наступному вигляді:

$$A=U\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] V^T\nonumber$$ $\sigma$де має форму $$\sigma =\left[ \begin{array}{ccc} \sigma _{1} & & 0 \\ & \ddots & \\ 0 & & \sigma _{k} \end{array} \right]\nonumber$$

Таким чином,$A^T=V\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] U^T$ і випливає, що $$A^TA=V\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] U^TU\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] V^T=V\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] V^T\nonumber$$ і так$A^TAV=V\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] .$ Аналогічно,$AA^TU=U\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] .$ Отже, ви знайдете ортонормальну основу власних векторів,$AA^T$ щоб зробити їх стовпцями матриці таким чином, що відповідні власні значення зменшуються. Це дає$U.$ Ви могли б потім зробити те ж саме$A^TA$ для отримання$V$.

Ми формалізуємо цю дискусію в наступній теоремі.

Теорема$\PageIndex{6}$: Singular Value Decomposition

$A$Дозволяти бути$m\times n$ матрицею. Тоді існують ортогональні матриці$U$ і$V$ відповідного розміру, такого,$\Sigma$ що$A= U \Sigma V^T$ де має форму $$\Sigma = \left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right]\nonumber$$ і$\sigma$ має форму $$\sigma =\left[ \begin{array}{ccc} \sigma _{1} & & 0 \\ & \ddots & \\ 0 & & \sigma _{k} \end{array} \right]\nonumber$$ для сингулярних значень$\sigma _{i}$$A.$

Доказ

Існує ортонормальна основа,$\left\{ \vec{v}_{i}\right\} _{i=1}^{n}$ така, що$A^TA\vec{v}_{i}=\sigma _{i}^{2}\vec{v}_{i}$ де$\sigma _{i}^{2}>0$ для$i=1,\cdots ,k,\left( \sigma _{i}>0\right)$ і дорівнює нулю, якщо$i>k.$ Таким чином для$i>k,$$A\vec{v}_{i}=\vec{0}$ тому, що $$A\vec{v}_{i}\cdot A\vec{v}_{i} = A^TA\vec{v}_{i} \cdot \vec{v}_{i} = \vec{0} \cdot \vec{v}_{i} =0.\nonumber$$ для For$i=1,\cdots ,k,$$\vec{u}_{i}\in \mathbb{R}^{m}$ визначають $$\vec{u}_{i}= \sigma _{i}^{-1}A\vec{v}_{i}.\nonumber$$

Таким чином,$A\vec{v}_{i}=\sigma _{i}\vec{u}_{i}.$ тепер $$\begin{aligned} \vec{u}_{i} \cdot \vec{u}_{j} &= \sigma _{i}^{-1}A \vec{v}_{i} \cdot \sigma _{j}^{-1}A\vec{v}_{j} = \sigma_{i}^{-1}\vec{v}_{i} \cdot \sigma _{j}^{-1}A^TA\vec{v}_{j} \\ &= \sigma _{i}^{-1}\vec{v}_{i} \cdot \sigma _{j}^{-1}\sigma _{j}^{2} \vec{v}_{j} = \frac{\sigma _{j}}{\sigma _{i}}\left( \vec{v}_{i} \cdot \vec{v}_{j}\right) =\delta _{ij}.\end{aligned}$$ Таким чином,$\left\{ \vec{u}_{i}\right\} _{i=1}^{k}$ є ортонормальний набір векторів в$\mathbb{R}^{m}.$ Також, $$AA^T\vec{u}_{i}=AA^T\sigma _{i}^{-1}A\vec{v}_{i}=\sigma _{i}^{-1}AA^TA\vec{v}_{i}=\sigma _{i}^{-1}A\sigma _{i}^{2}\vec{v} _{i}=\sigma _{i}^{2}\vec{u}_{i}.\nonumber$$ Тепер$\left\{ \vec{u}_{i}\right\} _{i=1}^{k}$$U$ поширюється на ортонормальну основу для всіх$\mathbb{R}^{m},\left\{ \vec{u}_{i}\right\} _{i=1}^{m}$ і нехай в $$U= \left[ \begin{array}{ccc} \vec{u}_{1} & \cdots & \vec{u}_{m} \end{array} \right ]\nonumber$$ той час як$V= \left( \vec{v}_{1}\cdots \vec{v}_{n}\right) .$ Таким чином матриця, яка має$\vec{u}_{i}$ як стовпці і$V$ є визначається як матриця, яка має стовпці$\vec{v}_{i}$ as. Тоді $$U^TAV=\left[ \begin{array}{c} \vec{u}_{1}^T \\ \vdots \\ \vec{u}_{k}^T \\ \vdots \\ \vec{u}_{m}^T \end{array} \right] A\left[ \vec{v}_{1}\cdots \vec{v}_{n}\right]\nonumber$$ $$=\left[ \begin{array}{c} \vec{u}_{1}^T \\ \vdots \\ \vec{u}_{k}^T \\ \vdots \\ \vec{u}_{m}^T \end{array} \right] \left[ \begin{array}{cccccc} \sigma _{1}\vec{u}_{1} & \cdots & \sigma _{k}\vec{u}_{k} & \vec{0} & \cdots & \vec{0} \end{array} \right] =\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right]\nonumber$$ де$\sigma$ дається в твердженні теореми.

Декомпозиція сингулярних значень має як безпосередній наслідок, який наведено в наступному цікавому результаті.

Слідство$\PageIndex{3}$: Rank and Singular Values

$A$Дозволяти бути$m\times n$ матрицею. Тоді ранг$A$ і$A^T$ дорівнює числу значень однини.

Обчислимо декомпозицію сингулярних значень простої матриці.

Приклад$\PageIndex{6}$: Singular Value Decomposition

Нехай$A=\left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right]$. Знайдіть декомпозицію сингулярних значень (SVD)$A$.

Рішення

Для початку обчислюємо$AA^T$ і$A^TA$. $$AA^T = \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \left[\begin{array}{rr} 1 & 3 \\ -1 & 1 \\ 3 & 1 \end{array}\right] = \left[\begin{array}{rr} 11 & 5 \\ 5 & 11 \end{array}\right].\nonumber$$

$$A^TA = \left[\begin{array}{rr} 1 & 3 \\ -1 & 1 \\ 3 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] = \left[\begin{array}{rrr} 10 & 2 & 6 \\ 2 & 2 & -2\\ 6 & -2 & 10 \end{array}\right].\nonumber$$

Оскільки$AA^T$ is$2\times 2$ while$A^T A$ is$3\times 3$,$AA^T$ і$A^TA$ мають однакові ненульові власні значення (за пропозицією$\PageIndex{1}$), ми обчислюємо характеристичний многочлен$c_{AA^T}(x)$ (тому що його простіше обчислити, ніж$c_{A^TA}(x)$).

$$\begin{aligned} c_{AA^T}(x)& = \det(xI-AA^T)= \left|\begin{array}{cc} x-11 & -5 \\ -5 & x-11 \end{array}\right|\\ & = (x-11)^2 - 25 \\ & = x^2-22x+121-25\\ & = x^2-22x+96\\ & = (x-16)(x-6)\end{aligned}$$

Тому власні значення$AA^T$ є$\lambda_1=16$ і$\lambda_2=6$.

Власні значення$A^TA$ є$\lambda_1=16$, і$\lambda_2=6$$\lambda_3=0$, і сингулярні значення$A$ є$\sigma_1=\sqrt{16}=4$ і$\sigma_2=\sqrt{6}$. За домовленістю ми перерахуємо власні значення (і відповідні однини) у незростаючому порядку (тобто від найбільшого до найменшого).

Щоб знайти матрицю$V$:

Для побудови матриці$V$ нам потрібно знайти власні вектори для$A^TA$. Оскільки власні значення$AA^T$ різних, відповідні власні вектори ортогональні, і нам потрібно лише нормалізувати їх.

$\lambda_1=16$: вирішити$(16I-A^TA)Y= 0$. $$\left[\begin{array}{rrr|r} 6 & -2 & -6 & 0 \\ -2 & 14 & 2 & 0 \\ -6 & 2 & 6 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} t \\ 0 \\ t \end{array}\right] =t\left[\begin{array}{r} 1 \\ 0 \\ 1 \end{array}\right], t\in \mathbb{R}.\nonumber$$

$\lambda_2=6$: вирішити$(6I-A^TA)Y= 0$. $$\left[\begin{array}{rrr|r} -4 & -2 & -6 & 0 \\ -2 & 4 & 2 & 0 \\ -6 & 2 & -4 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} -s \\ -s \\ s \end{array}\right] =s\left[\begin{array}{r} -1 \\ -1 \\ 1 \end{array}\right], s\in \mathbb{R}.\nonumber$$

$\lambda_3=0$: вирішити$(-A^TA)Y= 0$. $$\left[\begin{array}{rrr|r} -10 & -2 & -6 & 0 \\ -2 & -2 & 2 & 0 \\ -6 & 2 & -10 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & 1 & 0 \\ 0 & 1 & -2 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} -r \\ 2r \\ r \end{array}\right] =r\left[\begin{array}{r} -1 \\ 2 \\ 1 \end{array}\right], r\in \mathbb{R}.\nonumber$$

Нехай $$V_1=\frac{1}{\sqrt{2}}\left[\begin{array}{r} 1\\ 0\\ 1 \end{array}\right], V_2=\frac{1}{\sqrt{3}}\left[\begin{array}{r} -1\\ -1\\ 1 \end{array}\right], V_3=\frac{1}{\sqrt{6}}\left[\begin{array}{r} -1\\ 2\\ 1 \end{array}\right].\nonumber$$

Тоді $$V=\frac{1}{\sqrt{6}}\left[\begin{array}{rrr} \sqrt 3 & -\sqrt 2 & -1 \\ 0 & -\sqrt 2 & 2 \\ \sqrt 3 & \sqrt 2 & 1 \end{array}\right].\nonumber$$

Також, $$\Sigma = \left[\begin{array}{rrr} 4 & 0 & 0 \\ 0 & \sqrt 6 & 0 \end{array}\right],\nonumber$$ і використовуємо$A$$V^T$, і$\Sigma$ знайти$U$.

Так як$V$ ортогональний і$A=U\Sigma V^T$, з цього випливає$AV=U\Sigma$. Нехай$V=\left[\begin{array}{ccc} V_1 & V_2 & V_3 \end{array}\right]$, і нехай$U=\left[\begin{array}{cc} U_1 & U_2 \end{array}\right]$, де$U_1$ і$U_2$ є два стовпці$U$.

Тоді у нас є $$\begin{aligned} A\left[\begin{array}{ccc} V_1 & V_2 & V_3 \end{array}\right] &= \left[\begin{array}{cc} U_1 & U_2 \end{array}\right]\Sigma\\ \left[\begin{array}{ccc} AV_1 & AV_2 & AV_3 \end{array}\right] &= \left[\begin{array}{ccc} \sigma_1U_1 + 0U_2 & 0U_1 + \sigma_2 U_2 & 0 U_1 + 0 U_2 \end{array}\right] \\ &= \left[\begin{array}{ccc} \sigma_1U_1 & \sigma_2 U_2 & 0 \end{array}\right]\end{aligned}$$ що означає, що$AV_1=\sigma_1U_1 = 4U_1$ і$AV_2=\sigma_2U_2 = \sqrt 6 U_2$.

Таким чином, $$U_1 = \frac{1}{4}AV_1 = \frac{1}{4} \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \frac{1}{\sqrt{2}}\left[\begin{array}{r} 1\\ 0\\ 1 \end{array}\right] = \frac{1}{4\sqrt 2}\left[\begin{array}{r} 4\\ 4 \end{array}\right] = \frac{1}{\sqrt 2}\left[\begin{array}{r} 1\\ 1 \end{array}\right],\nonumber$$ а $$U_2 = \frac{1}{\sqrt 6}AV_2 = \frac{1}{\sqrt 6} \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \frac{1}{\sqrt{3}}\left[\begin{array}{r} -1\\ -1\\ 1 \end{array}\right] =\frac{1}{3\sqrt 2}\left[\begin{array}{r} 3\\ -3 \end{array}\right] =\frac{1}{\sqrt 2}\left[\begin{array}{r} 1\\ -1 \end{array}\right].\nonumber$$ отже, $$U=\frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right],\nonumber$$ і $$\begin{aligned} A & = \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right]\\ & = \left(\frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right]\right) \left[\begin{array}{rrr} 4 & 0 & 0 \\ 0 & \sqrt 6 & 0 \end{array}\right] \left(\frac{1}{\sqrt{6}}\left[\begin{array}{rrr} \sqrt 3 & 0 & \sqrt 3 \\ -\sqrt 2 & -\sqrt 2 & \sqrt2 \\ -1 & 2 & 1 \end{array}\right]\right).\end{aligned}$$

Ось ще один приклад.

Приклад$\PageIndex{7}$: Finding the SVD

Знайдіть SVD для$A=\left[\begin{array}{r} -1 \\ 2\\ 2 \end{array}\right]$.

Рішення

Так як$A$$A^T A$ is$3\times 1$, є$1\times 1$ матрицею, власні значення якої знайти легше, ніж власні значення$3\times 3$ матриці$AA^T$.

$$A^TA=\left[\begin{array}{ccc} -1 & 2 & 2 \end{array}\right] \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] =\left[\begin{array}{r} 9 \end{array}\right].\nonumber$$

Таким чином$A^TA$ має власне значення$\lambda_1=9$, і власні значення$AA^T$ are$\lambda_1=9$$\lambda_2=0$, і$\lambda_3=0$. Крім того,$A$ має лише одне значення однини,$\sigma_1=3$.

Щоб знайти матрицю$V$: Для цього ми знаходимо власний вектор для$A^TA$ і нормалізуємо його. У цьому випадку знаходження одиниці власноговектора тривіально:$V_1=\left[\begin{array}{r} 1 \end{array}\right]$, і $$V=\left[\begin{array}{r} 1 \end{array}\right].\nonumber$$

Також$\Sigma =\left[\begin{array}{r} 3 \\ 0\\ 0 \end{array}\right]$, і використовуємо$A$$V^T$, і$\Sigma$ знайти$U$.

Тепер$AV=U\Sigma$, з$V=\left[\begin{array}{r} V_1 \end{array}\right]$, і$U=\left[\begin{array}{rrr} U_1 & U_2 & U_3 \end{array}\right]$$U_1$, де$U_2$, і$U_3$ є стовпцями$U$. Таким чином, $$\begin{aligned} A\left[\begin{array}{r} V_1 \end{array}\right] &= \left[\begin{array}{rrr} U_1 & U_2 & U_3 \end{array}\right]\Sigma\\ \left[\begin{array}{r} AV_1 \end{array}\right] &= \left[\begin{array}{r} \sigma_1 U_1+0U_2+0U_3 \end{array}\right]\\ &= \left[\begin{array}{r} \sigma_1 U_1 \end{array}\right]\end{aligned}$$ Це дає нам$AV_1=\sigma_1 U_1= 3U_1$, так $$U_1 = \frac{1}{3}AV_1 = \frac{1}{3} \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] \left[\begin{array}{r} 1 \end{array}\right] = \frac{1}{3} \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right].\nonumber$$

Вектори$U_2$ і$U_3$ є власними векторами,$AA^T$ відповідними власному значенню$\lambda_2=\lambda_3=0$. Замість розв'язання системи$(0I-AA^T)X= 0$ та подальшого використання процесу Грама-Шмідта на результуючій множині двох основних власних векторів може бути використаний наступний підхід.

Знайдіть вектори$U_2$ і$U_3$ спочатку поширюючи$\{ U_1\}$ на основу$\mathbb{R}^3$, потім використовуючи алгоритм Грама-Шмідта для ортогоналізації основи, і, нарешті, нормалізуючи вектори.

Починаючи з$\{ 3U_1 \}$ замість того$\{ U_1 \}$, щоб зробити арифметику трохи простіше. Це легко перевірити, що $$\left\{ \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right], \left[\begin{array}{r} 1 \\ 0 \\ 0 \end{array}\right], \left[\begin{array}{r} 0 \\ 1 \\ 0 \end{array}\right]\right\}\nonumber$$ є основою$\mathbb{R}^3$. Встановіть $$E_1 = \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right], X_2 = \left[\begin{array}{r} 1 \\ 0 \\ 0 \end{array}\right], X_3 =\left[\begin{array}{r} 0 \\ 1 \\ 0 \end{array}\right],\nonumber$$ і застосуйте алгоритм Грама-Шмідта до$\{ E_1, X_2, X_3\}$.

Це дає нам $$E_2 = \left[\begin{array}{r} 4 \\ 1 \\ 1 \end{array}\right] \mbox{ and } E_3 = \left[\begin{array}{r} 0 \\ 1 \\ -1 \end{array}\right].\nonumber$$

Тому $$U_2 = \frac{1}{\sqrt{18}} \left[\begin{array}{r} 4 \\ 1 \\ 1 \end{array}\right], U_3 = \frac{1}{\sqrt 2} \left[\begin{array}{r} 0 \\ 1 \\ -1 \end{array}\right],\nonumber$$ і $$U = \left[\begin{array}{rrr} -\frac{1}{3} & \frac{4}{\sqrt{18}} & 0 \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & \frac{1}{\sqrt 2} \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & -\frac{1}{\sqrt 2} \end{array}\right].\nonumber$$

Нарешті, $$A = \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] = \left[\begin{array}{rrr} -\frac{1}{3} & \frac{4}{\sqrt{18}} & 0 \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & \frac{1}{\sqrt 2} \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & -\frac{1}{\sqrt 2} \end{array}\right] \left[\begin{array}{r} 3 \\ 0 \\ 0 \end{array}\right] \left[\begin{array}{r} 1 \end{array}\right].\nonumber$$

Розглянемо ще один приклад.

Приклад$\PageIndex{8}$: Find the SVD

Знайти декомпозицію сингулярних значень для матриці $$A= \left[ \begin{array}{ccc} \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \end{array} \right]\nonumber$$

Рішення

Спочатку розглянемо$A^TA$ $$\left[ \begin{array}{ccc} \frac{16}{5} & \frac{32}{5} & 0 \\ \frac{32}{5} & \frac{64}{5} & 0 \\ 0 & 0 & 0 \end{array} \right]\nonumber$$ Що таке власні значення та власні вектори? Деякі обчислення показують, що це $$\left\{ \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] ,\left[ \begin{array}{c} -\frac{2}{5}\sqrt{5} \\ \frac{1}{5}\sqrt{5} \\ 0 \end{array} \right] \right\} \leftrightarrow 0,\left\{ \left[ \begin{array}{c} \frac{1}{5}\sqrt{5} \\ \frac{2}{5}\sqrt{5} \\ 0 \end{array} \right] \right\} \leftrightarrow 16\nonumber$$ Таким чином матриця$V$ задається $$V=\left[ \begin{array}{ccc} \frac{1}{5}\sqrt{5} & -\frac{2}{5}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{5} & \frac{1}{5}\sqrt{5} & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber$$ Далі розглянемо$AA^T$ $$\left[ \begin{array}{cc} 8 & 8 \\ 8 & 8 \end{array} \right]\nonumber$$ власні вектори і власні значення $$\left\{ \left[ \begin{array}{c} -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} \end{array} \right] \right\} \leftrightarrow 0,\left\{ \left[ \begin{array}{c} \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} \end{array} \right] \right\} \leftrightarrow 16\nonumber$$ Таким чином, ви можете дозволити$U$ бути задані $$U=\left[ \begin{array}{cc} \frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{array} \right]\nonumber$$ Давайте перевіримо це. $U^TAV=$ $$\left[ \begin{array}{cc} \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{array} \right] \left[ \begin{array}{ccc} \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \end{array} \right] \left[ \begin{array}{ccc} \frac{1}{5}\sqrt{5} & -\frac{2}{5}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{5} & \frac{1}{5}\sqrt{5} & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber$$ $$=\left[ \begin{array}{ccc} 4 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]\nonumber$$

Це ілюструє, що якщо у вас є хороший спосіб знайти власні вектори та власні значення для Ермітієвої матриці, яка має невід'ємні власні значення, то у вас також є хороший спосіб знайти декомпозицію сингулярних значень довільної матриці.

Позитивні визначені матриці

Позитивні певні матриці часто зустрічаються в додатках такої механіки і статистики.

Почнемо з визначення.

Визначення$\PageIndex{5}$: Positive Definite Matrix

$A$Дозволяти$n \times n$ симетричною матрицею. Тоді$A$ є додатним визначенням, якщо всі його власні значення позитивні.

Зв'язок між негативною визначеною матрицею і позитивною певною матрицею виглядає наступним чином.

Лемма$\PageIndex{2}$: Negative Definite Matrix

$n\times n$$A$Матриця від'ємна, визначена тоді і тільки тоді$-A$, коли позитивна визначена

Розглянемо наступну лему.

Лемма$\PageIndex{3}$: Positive Definite Matrix and Invertibility

Якщо$A$ позитивний певний, то він є оборотним.

Доказ

If$A\vec{v}=\vec{0},$$0$ then є власним значенням$\vec{v}$ if ненульовим, що не відбувається для додатної певної матриці. Звідси$\vec{v}=\vec{0}$ і$A$ так один до одного. Цього достатньо, щоб зробити висновок, що він є оборотним.

Зверніть увагу, що ця лема означає, що якщо$A$ матриця позитивна визначена, то$\det(A) > 0$.

Наступна теорема дає ще одну характеристику позитивних певних матриць. Це дає корисний тест для перевірки того, чи матриця є позитивною визначеною.

Теорема$\PageIndex{7}$: Positive Definite Matrix

$A$Дозволяти симетричною матрицею. Тоді$A$ позитивний визначений, якщо і тільки якщо$\vec{x}^T A \vec{x}$ є позитивним для всіх ненульових$\vec{x} \in \mathbb{R}^n$.

Доказ

Оскільки$A$ є симетричним, існує ортогональна матриця,$U$ так що $$U^{T}AU=diag(\lambda_1,\lambda_2,\ldots,\lambda_n)=D,\nonumber$$ де$\lambda_1,\lambda_2,\ldots,\lambda_n$ знаходяться (не обов'язково відмінні) власні значення$A$. Нехай$\vec{x}\in\mathbb{R}^n$$\vec{x}\neq \vec{0}$, і визначити$\vec{y}=U^T\vec{x}$. Тоді $$\vec{x}^TA\vec{x}=\vec{x}^T(UDU^T)\vec{x} = (\vec{x}^TU)D(U^T\vec{x}) =\vec{y}^TD\vec{y}.\nonumber$$

Написання$\vec{y}^T=\left[\begin{array}{cccc} y_1 & y_2 & \cdots & y_n\end{array}\right]$, $$\begin{aligned} \vec{x}^TA\vec{x} & = \left[\begin{array}{cccc} y_1 & y_2 & \cdots & y_n\end{array}\right] diag(\lambda_1,\lambda_2,\ldots,\lambda_n) \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n\end{array}\right]\\ & = \lambda_1 y_1^2 + \lambda_2 y_2^2 + \cdots \lambda_n y_n^2.\end{aligned}$$

$(\Rightarrow)$Спочатку ми будемо вважати, що$A$ позитивно визначено і довести, що$\vec{x}^T A \vec{x}$ є позитивним.

$A$Припустимо, позитивний певний, і$\vec{x}\in\mathbb{R}^n$,$\vec{x}\neq\vec{0}$. Так як$U^T$ є оборотним$\vec{y}=U^T\vec{x}\neq \vec{0}$, і, таким чином,$y_j\neq 0$ для деяких$j$, має$y_j^2>0$ на увазі для деяких$j$. Крім того, оскільки всі власні значення$A$ є додатними,$\lambda_i y_i^2\geq 0$ для всіх$i$ і$\lambda_jy_j^2>0$. Тому,$\vec{x}^TA\vec{x}>0$.

$(\Leftarrow)$Зараз ми припустимо$\vec{x}^T A \vec{x}$ позитивне і покажемо,$A$ що позитивно визначено.

Якщо$\vec{x}^TA\vec{x}>0$ всякий раз$\vec{x}\neq \vec{0}$$\vec{x}=U\vec{e}_j$, виберіть, де$\vec{e}_j$ знаходиться$j^{\mbox{th}}$ стовпець$I_n$. Оскільки$U$ є оборотним$\vec{x}\neq\vec{0}$, і таким чином $$\vec{y}=U^T\vec{x}=U^T(U\vec{e}_j) =\vec{e}_j.\nonumber$$ Таким чином$y_j=1$ і$y_i=0$ коли$i\neq j$, так $$\lambda_1 y_1^2 + \lambda_2 y_2^2 + \cdots \lambda_n y_n^2 =\lambda_j,\nonumber$$ тобто,$\lambda_j=\vec{x}^TA\vec{x}>0$. Тому$A$ позитивний певний.

Є й інші дуже цікаві наслідки, які є результатом позитивного визначення матриці. Спочатку можна відзначити, що властивість бути додатним визначенням передається до кожної з головних підматриць, які ми зараз визначимо.

Визначення$\PageIndex{6}$: The Submatrix $A_k$

$A$Дозволяти бути$n\times n$ матрицею. $A_{k}$Позначте$k\times k$ матрицею, отриманою видаленням$k+1,\cdots ,n$ стовпців і$k+1,\cdots ,n$ рядків з$A.$ Таким чином$A_{n}=A$ і$A_{k}$ є$k\times k$ підматрицею$A$ якої займає верхній лівий кут$A.$

Лемма$\PageIndex{4}$: Positive Definite and Submatrices

$A$Дозволяти бути$n\times n$ позитивною визначеною матрицею. Тоді кожна$A_{k}$ підматриця також позитивна визначена.

Доказ

Це випливає відразу з наведеного вище визначення. $\vec{x}\in \mathbb{R}^{k}$Дозволяти бути ненульовим. Тоді $$\vec{x}^{T}A_{k}\vec{x}=\left[ \begin{array}{cc} \vec{x}^{T} & 0 \end{array} \right] A\left[ \begin{array}{c} \vec{x} \\ 0 \end{array} \right] > 0\nonumber$$ за припущенням,$A$ що позитивно визначено.

Існує ще один спосіб розпізнати, чи є матриця позитивною визначеною, яка описана термінами цих підматриць. Викладаємо результат, доказ якого можна знайти в більш просунутих текстах.

Теорема$\PageIndex{8}$: Positive Matrix and Determinant of $A_k$

$A$Дозволяти симетричною матрицею. Тоді$A$ позитивний визначений, якщо і тільки$\det \left( A_{k}\right)$ якщо більше, ніж$0$ для кожної підматриці$A_{k}$,$k=1,\cdots ,n$.

Доказ

Ми доводимо цю теорему індукцією на$n.$ Це явно вірно, якщо$n=1.$ Припустимо, що це вірно для$n-1$ де$n\geq 2$. Так як$\det \left( A\right) =\det \left( A_{n}\right) >0,$ випливає, що всі власні значення ненульові. Потрібно показати, що всі вони позитивні. Припустимо, що ні. Тоді є деяке парне число з них, які є негативними, навіть тому, що добуток всіх власних значень, як відомо, позитивний, рівний$\det \left( A\right)$. Виберіть два,$\lambda _{1}$$\lambda _{2}$ і нехай$A \vec{u}_{i}=\lambda _{i}\vec{u}_{i}$ де$\vec{u}_{i}\neq \vec{0}$ для$i=1,2$ і$\vec{u}_{1}\cdot \vec{u}_{2}=0.$ тепер, якщо$\vec{y}\equiv \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}$ є елементом$span\left\{ \vec{u}_{1},\vec{u}_{2}\right\} ,$ тоді, так як це власні значення і$\ \vec{u}_{1}\cdot \vec{u}_{2}=0,$ короткий обчислення показує $$\left( \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}\right) ^{T}A\left( \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}\right)\nonumber$$ $$=\left\vert \alpha _{1}\right\vert ^{2}\lambda _{1} \vec{u} _{1} ^{2}+\left\vert \alpha _{2}\right\vert ^{2}\lambda _{2}\vec{u}_{2}^{2}<0.\nonumber$$ Тепер дозволяючи$\vec{x}\in \mathbb{R}^{n-1},$ нам використовувати індукцію гіпотеза написати $$\left[ \begin{array}{cc} x^{T} & 0 \end{array} \right] A\left[ \begin{array}{c} \vec{x} \\ 0 \end{array} \right] =\vec{x}^{T}A_{n-1}\vec{x}>0.\nonumber$$ Тепер розмірність$\left\{ \vec{z}\in \mathbb{R}^{n}:z_{n}=0\right\}$ є$n-1$ і розмірність$span\left\{ \vec{u}_{1},\vec{u} _{2}\right\} =2$ і тому має бути деякий ненульовий,$\vec{x}\in \mathbb{R} ^{n}$ який знаходиться в обох цих підпросторах$\mathbb{R}^{n}$. Однак перше обчислення вимагатиме, що$\vec{x}^{T}A\vec{x}<0$ тоді як друге вимагатиме$\vec{x}^{T}A\vec{x}>0.$ цього протиріччя показує, що всі власні значення повинні бути позитивними. Це доводить if частина теореми. Зворотне також може бути показано правильним, але це напрямок, який тільки що був показаний, який представляє найбільший інтерес.

Слідство$\PageIndex{4}$: Symmetric and Negative Definite Matrix

$A$Дозволяти симетричним. Тоді$A$ негативний визначено, якщо і тільки якщо $$\left( -1\right) ^{k} \det \left( A_{k}\right) >0\nonumber$$ для кожного$k=1,\cdots ,n$.

Доказ

Це безпосередньо від вищезгаданої теореми, коли ми помічаємо, що$A$ є негативним визначенням, якщо і тільки тоді, коли$-A$ позитивно визначено. Тому, якщо$\det \left( -A_{k}\right) >0$ для всіх$k=1,\cdots ,n,$ випливає,$A$ що негативний певний. Однак,$\det \left( -A_{k}\right) =\left( -1\right) ^{k}\det \left( A_{k}\right) .$

Факторизація Холеського

Ще однією важливою теоремою є існування специфічної факторизації позитивних певних матриць. Вона називається факторизацією Холеського і множить матрицю в добуток верхньої трикутної матриці та її транспонування.

Теорема$\PageIndex{9}$: Cholesky Factorization

$A$Дозволяти бути позитивною визначеною матрицею. Тоді існує верхня трикутна матриця, основні діагональні записи$U$ якої позитивні, такі, що$A$ можна записати $$A= U^TU\nonumber$$ Ця факторизація є унікальною.

Процес знаходження такої матриці$U$ спирається на прості операції з рядками.

Порядок дій$\PageIndex{1}$: Finding the Cholesky Factorization

$A$Дозволяти бути позитивною визначеною матрицею. Матрицю$U$, яка створює факторизацію Холеського, можна знайти через два етапи.

1. Використовуючи лише тип$3$ елементарних рядкових операцій (кратні рядки, додані до інших рядків) ставлять$A$ у верхній трикутній формі. Назвіть цю матрицю$\hat{U}$. Потім$\hat{U}$ має позитивні записи на головній діагоналі.
2. Розділіть кожен ряд$\hat{U}$ на квадратний корінь діагонального запису в цьому рядку. В результаті виходить матриця$U$.

Звичайно, ви завжди можете переконатися, що ваша факторизація правильна, множивши$U$ і$U^T$ переконатися, що результат є вихідною матрицею$A$.

Розглянемо наступний приклад.

Приклад$\PageIndex{9}$: Cholesky Factorization

Покажіть, що$A=\left[\begin{array}{rrr} 9 & -6 & 3 \\ -6 & 5 & -3 \\ 3 & -3 & 6 \end{array}\right]$ є позитивним визначенням, і знайдіть факторизацію Холеського$A$.

Рішення

Спочатку ми покажемо,$A$ що позитивно визначено. За теоремою$\PageIndex{8}$ досить показати, що детермінант кожної підматриці позитивний. $$A_{1}=\left[\begin{array}{c} 9 \end{array}\right] \mbox{ and } A_{2}=\left[\begin{array}{rr} 9 & -6 \\ -6 & 5 \end{array}\right],\nonumber$$ так$\det(A_{1})=9$ і$\det(A_{2})=9$. Так як$\det(A)=36$, випливає,$A$ що позитивно визначено.

Тепер ми використовуємо процедуру$\PageIndex{1}$, щоб знайти факторизацію Холеського. Row reduce (використовуючи тільки операції типу$3$ рядків) до отримання верхньої трикутної матриці. $$\left[\begin{array}{rrr} 9 & -6 & 3 \\ -6 & 5 & -3 \\ 3 & -3 & 6 \end{array}\right] \rightarrow \left[\begin{array}{rrr} 9 & -6 & 3 \\ 0 & 1 & -1 \\ 0 & -1 & 5 \end{array}\right] \rightarrow \left[\begin{array}{rrr} 9 & -6 & 3 \\ 0 & 1 & -1 \\ 0 & 0 & 4 \end{array}\right]\nonumber$$

Тепер розділіть записи в кожному рядку на квадратний корінь діагонального запису в цьому рядку, щоб дати $$U=\left[\begin{array}{rrr} 3 & -2 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 2 \end{array}\right]\nonumber$$

Ви можете це перевірити$U^TU = A$.

Приклад$\PageIndex{10}$: Cholesky Factorization

$A$Дозволяти бути додатною визначеною матрицею, заданою $$\left[ \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 4 & 2 \\ 1 & 2 & 5 \end{array} \right]\nonumber$$ Визначити її факторизацію Холеського.

Рішення

Ви можете переконатися, що насправді$A$ є позитивним певним.

Щоб знайти факторизацію Холеського, ми перший рядок зменшуємо до верхньої трикутної матриці. $$\left[ \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 4 & 2 \\ 1 & 2 & 5 \end{array} \right] \rightarrow \left[ \begin{array}{ccc} 3 & 1 & 1 \\ 0 & \frac{11}{3} & \frac{5}{3} \\ 0 & \frac{5}{3} & \frac{14}{5} \end{array} \right] \rightarrow \left[ \begin{array}{ccc} 3 & 1 & 1 \\ 0 & \frac{11}{3} & \frac{5}{3} \\ 0 & 0 & \frac{43}{11} \end{array} \right]\nonumber$$

Тепер розділіть записи в кожному рядку на квадратний корінь діагонального запису в цьому рядку і спростіть. $$U = \left[ \begin{array}{ccc} \sqrt{3} & \frac{1}{3}\sqrt{3} & \frac{1}{3}\sqrt{3} \\ 0 & \frac{1}{3}\sqrt{3}\sqrt{11} & \frac{5}{33}\sqrt{3}\sqrt{11} \\ 0 & 0 & \frac{1}{11}\sqrt{11}\sqrt{43} \end{array} \right]\nonumber$$

QR-факторизація

У цьому розділі вивчається достовірна факторизація матриць. $QR$Називається факторизацією матриці, вона завжди існує. Хоча багато можна сказати про$QR$ факторизацію, цей розділ буде обмежений реальними матрицями. Тому ми припускаємо, що точковий добуток, який використовується нижче, є звичайним точковим твором. Почнемо з визначення.

Визначення$\PageIndex{7}$: $QR$Factorization

$A$Дозволяти бути реальною$m\times n$ матрицею. Тоді$QR$ факторизація$A$ складається з двох матриць,$Q$ ортогональних і$R$ верхніх трикутних, таких, що$A=QR.$

арфакторизація

Наступна теорема стверджує, що така факторизація існує.

Теорема$\PageIndex{10}$: Existence of $QR$Factorization

$A$Дозволяти будь-яка реальна$m\times n$ матриця з лінійно незалежними стовпцями. Потім існує ортогональна матриця$Q$ і верхня трикутна матриця,$R$ що має невід'ємні записи на головній діагоналі такі, що $$A=QR\nonumber$$

Порядок отримання$QR$ факторизації для будь-якої матриці виглядає$A$ наступним чином.

Порядок дій$\PageIndex{2}$: $QR$Factorization

$A$Дозволяти$m \times n$ матриця, задана$A = \left[ \begin{array}{cccc} A_1 & A_2 & \cdots & A_n \end{array} \right]$ де$A_i$ є лінійно незалежні стовпці$A$.

1. Застосовуємо процес Грама-Шмідта 4.11.1 до стовпців$A$,$B_i$ записуючи для отриманих стовпців.
2. Нормалізувати$B_i$, знайти$C_i = \frac{1}{ B_i } B_i$.
3. Побудувати ортогональну матрицю$Q$ як$Q=\left[ \begin{array}{cccc} C_1 & C_2 & \cdots & C_n \end{array} \right]$.
4. Побудувати верхню трикутну матрицю$R$ як $$R = \left[ \begin{array}{ccccc} B_1 & A_2 \cdot C_1 & A_3 \cdot C_1 & \cdots & A_n \cdot C_1 \\ 0 & B_2 & A_3 \cdot C_2 & \cdots & A_n \cdot C_2 \\ 0 & 0 & B_3 & \cdots & A_n \cdot C_3 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & B_n \end{array} \right]\nonumber$$
5. Нарешті, запишіть,$A=QR$ де$Q$ знаходиться ортогональна матриця і$R$ верхня трикутна матриця, отримана вище.

Зверніть увагу, що$Q$ це ортогональна матриця, як$C_i$ форма ортонормальної множини. Оскільки$B_i > 0$ для всіх$i$ (так як довжина вектора завжди позитивна), то випливає, що$R$ це верхня трикутна матриця з позитивними записами на головній діагоналі.

Розглянемо наступний приклад.

Приклад$\PageIndex{11}$: Finding a $QR$Factorization

Нехай $$A = \left[ \begin{array}{rr} 1 & 2 \\ 0 & 1 \\ 1 & 0 \end{array} \right]\nonumber$$ Знайти ортогональну матрицю$Q$ і верхню трикутну матрицю$R$ такі, що$A=QR$.

Рішення

По-перше, зауважте$A_1$$A_2$, що, стовпці$A$, є лінійно незалежними. Тому ми можемо використовувати процес Грама-Шмідта для створення відповідного ортогонального набору$\left\{ B_1, B_2 \right\}$ наступним чином: $$\begin{aligned} B_1 &= A_1 = \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ B_2 &= A_2 - \frac{A_2 \cdot B_1}{ B_1 ^2} B_1 \\ &= \left[ \begin{array}{r} 2 \\ 1 \\ 0 \end{array} \right] - \frac{2}{2} \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \right]\end{aligned}$$

Нормалізуйте кожен вектор, щоб створити набір$\left\{ C_1, C_2 \right\}$ наступним чином: $$\begin{aligned} C_1 &= \frac{1}{ B_1 } B_1 = \frac{1}{\sqrt{2}} \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ C_2 &= \frac{1}{ B_2 } B_2 = \frac{1}{\sqrt{3}} \left[ \begin{array}{r} 1 \\ 1 \\ -1 \end{array}\right]\end{aligned}$$

Тепер побудуйте ортогональну матрицю$Q$ як $$\begin{aligned} Q &= \left[ \begin{array}{cccc} C_1 & C_2 & \cdots & C_n \end{array} \right] \\ &= \left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ 0 & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{3}} \end{array} \right]\end{aligned}$$

Нарешті, побудуйте верхню трикутну матрицю$R$ як $$\begin{aligned} R &= \left[ \begin{array}{cc} B_1 & A_2 \cdot C_1 \\ 0 & B_2 \end{array} \right] \\ &= \left[ \begin{array}{cc} \sqrt{2} & \sqrt{2} \\ 0 & \sqrt{3} \\ \end{array} \right]\end{aligned}$$

Це залишається читачеві, щоб перевірити це$A=QR$.

$QR$Факторизація та власні значення

$QR$Факторизація матриці має дуже корисне застосування. Виявляється, його можна використовувати неодноразово для оцінки власних значень матриці. Розглянемо наступний порядок дій.

Порядок дій$\PageIndex{3}$: Using the $QR$ Factorization to Estimate Eigenvalues

$A$Дозволяти бути оборотною матрицею. Визначте матриці$A_1, A_2, \cdots$ наступним чином:

1. $A_1 = A$враховується як$A_1 = Q_1R_1$
2. $A_2 = R_1Q_1$враховується як$A_2 = Q_2R_2$
3. $A_3 = R_2Q_2$враховується як$A_3 = Q_3R_3$

Продовжуйте таким чином, де взагалі$A_k = Q_kR_k$ і$A_{k+1} = R_kQ_k$.

Потім випливає, що ця послідовність$A_i$ сходиться до верхньої трикутної матриці, яка аналогічна$A$. Тому власні значення$A$ можуть бути наближені записами на головній діагоналі цієї верхньої трикутної матриці.

Способи харчування

Хоча$QR$ алгоритм може бути використаний для обчислення власних значень, існує корисна і досить елементарна методика знаходження власного вектора та пов'язаного з ним власного значення, найближчого до заданого комплексного числа, який називається методом зміщеної оберненої потужності. Він, як правило, працює дуже добре за умови, що ви починаєте з чогось, що досить близько до власне значення.

Силові методи засновані на розгляді повноважень даної матриці. $\left\{ \vec{x}_{1},\cdots ,\vec{x}_{n}\right\}$Дозволяти бути основою власних векторів для$\mathbb{C}^{n}$ таких, що$A\vec{x}_{n}=\lambda _{n}\vec{x}_{n}.$ Тепер нехай$\vec{u}_{1}$ буде деякий ненульовий вектор. Оскільки$\left\{ \vec{x}_{1},\cdots ,\vec{x}_{n}\right\}$ є основою, існують унікальні скаляри,$c_{i}$ такі що $$\vec{u}_{1}=\sum_{k=1}^{n}c_{k}\vec{x}_{k}\nonumber$$ Припустимо, що вам не так пощастило, щоб вибрати$\vec{u}_{1}$ таким чином, що$c_{n}=0.$ Тоді нехай$A\vec{u}_{k}=\vec{u}_{k+1}$ так, що $$\vec{u}_{m}=A^{m}\vec{u}_{1}=\sum_{k=1}^{n-1}c_{k}\lambda _{k}^{m}\vec{x} _{k}+\lambda _{n}^{m}c_{n}\vec{x}_{n}. \label{20maye1}$$ Для великих$m$ останній термін, досить добре$\lambda _{n}^{m}c_{n}\vec{x}_{n},$ визначає напрямок вектора праворуч. $\left\vert \lambda _{n}\right\vert$Це тому, що більше, ніж$\left\vert \lambda _{k}\right\vert$ для$k<n$ і тому для великої$m,$ суми,$\sum_{k=1}^{n-1}c_{k}\lambda _{k}^{m}\vec{x}_{k},$ праворуч досить незначна. Тому для великих$m,$$\vec{u}_{m}$ по суті кратний власному вектору$\vec{x}_{n},$ той, який йде з$\lambda _{n}.$ Єдина проблема полягає в тому, що немає контролю розміру векторів$\vec{u}_{m}.$ Ви можете виправити це масштабуванням. Дозвольте$S_{2}$ позначати запис$A\vec{u}_{1}$ якого найбільша за абсолютною величиною. Ми називаємо це коефіцієнтом масштабування. Тоді$\vec{u}_{2}$ буде не просто,$A\vec{u}_{1}$ але$A\vec{u}_{1}/S_{2}.$ Далі давайте$S_{3}$ позначимо запис$A\vec{u}_{2}$ якого має найбільше абсолютне значення і визначте$\vec{u}_{3}\equiv A\vec{u}_{2}/S_{3}.$ Продовжити таким чином. Щойно описане масштабування не руйнує відносну нікчемність терміна, що включає суму в$\eqref{20maye1}$. Дійсно, це становить не що інше, як зміна одиниць довжини. Також зверніть увагу, що від цієї процедури масштабування абсолютне значення найбільшого елемента завжди$\vec{u}_{k}$ дорівнює 1. Тому для великих$m,$ $$\vec{u}_{m}= \frac{\lambda _{n}^{m}c_{n}\vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}+\left( \text{relatively insignificant term}\right) .\nonumber$$ Отже, запис$A\vec{u}_{m}$ якого має найбільше абсолютне значення, по суті дорівнює запису, що має найбільше абсолютне значення, $$A\left( \frac{\lambda _{n}^{m}c_{n}\vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}\right) = \frac{\lambda _{n}^{m+1}c_{n} \vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}\approx \lambda _{n}\vec{u}_{m}\nonumber$$ і тому для великих$m,$ це повинно бути так, що$\lambda _{n}\approx S_{m+1}.$ Це передбачає наступну процедуру.

Порядок дій$\PageIndex{4}$: Finding the Largest Eigenvalue with its Eigenvector

1. Почніть з вектора$\vec{u}_{1}$, який, як ви сподіваєтеся, має компонент у напрямку Вектор$\left( 1,\cdots ,1\right) ^{T}$, як правило, досить хороший вибір.$\vec{x}_{n}.$
2. Якщо$\vec{u}_{k}$ відомо, $$\vec{u}_{k+1}=\frac{A\vec{u}_{k}}{S_{k+1}}\nonumber$$ де$S_{k+1}$ знаходиться запис$A\vec{u}_{k}$ якого має найбільше абсолютне значення.
3. Коли коефіцієнти масштабування, не сильно$S_{k}$ змінюються,$S_{k+1}$ будуть близькі до власного значення і$\vec{u}_{k+1}$ будуть близькі до власного вектора.
4. Перевірте свою відповідь, щоб перевірити, чи добре вона працювала.

Метод зміщеної оберненої потужності передбачає знаходження власного значення, найближчого до заданого комплексного числа разом з пов'язаним власним значенням. Якщо$\mu$ є комплексним числом, і ви хочете знайти те,$\lambda$ що найближче до$\mu ,$ вас можна розглянути власні значення та власні вектори$\left( A-\mu I\right) ^{-1}$. Тоді,$A\vec{x}=\lambda \vec{x}$ якщо і тільки $$\left( A-\mu I\right) \vec{x}=\left( \lambda -\mu \right) \vec{x}\nonumber$$ якщо якщо і тільки якщо $$\frac{1}{\lambda -\mu }\vec{x}=\left( A-\mu I\right) ^{-1}\vec{x}\nonumber$$ Таким чином, якщо$\lambda$ є найближчим власним значенням$A$ до$\mu$ то з усіх власних значень з$\left( A-\mu I\right) ^{-1},$ вас$\frac{1}{ \lambda -\mu }$ буде найбільшим. Таким чином, все, що вам потрібно зробити, це застосувати метод потужності до$\left( A-\mu I\right) ^{-1}$ і власним вектором, який ви отримаєте, буде власним вектором, який відповідає$\lambda$ де$\lambda$ є найближчим до$\mu$ всіх власних значень$A$. Ви можете скористатися власним вектором, щоб визначити це безпосередньо.

Приклад$\PageIndex{12}$: Finding Eigenvalue and Eigenvector

Знайти власні значення і власний вектор, для $$\left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right]\nonumber$$ яких найближче до$.9+.9i$.

Рішення

$$\left ( \left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right] - (.9+.9i)\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \right )^{-1}\nonumber$$

$$= \left[ \begin{array}{ccc} -0.619\,19-10.\, 545i & -5.\, 524\,9-4.\, 972\,4i & -0.370\,57-5.\, 821\,3i \\ 5.\, 524\,9+4.\, 972\,4i & 5.\, 276\,2+0.248\,62i & 2.\, 762\,4+2.\, 486\,2i \\ 0.741\,14+11.\, 643i & 5.\, 524\,9+4.\, 972\,4i & 0.492\,52+6.\, 918\,9i \end{array} \right]\nonumber$$

Потім виберіть початкове припущення множення на цю матрицю, підняту до великої потужності. $$= \left[ \begin{array}{ccc} -0.619\,19-10.\, 545i & -5.\, 524\,9-4.\, 972\,4i & -0.370\,57-5.\, 821\,3i \\ 5.\, 524\,9+4.\, 972\,4i & 5.\, 276\,2+0.248\,62i & 2.\, 762\,4+2.\, 486\,2i \\ 0.741\,14+11.\, 643i & 5.\, 524\,9+4.\, 972\,4i & 0.492\,52+6.\, 918\,9i \end{array} \right]^{15}\left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right]\nonumber$$

Це дорівнює $$\left[ \begin{array}{c} 1.\, 562\,9\times 10^{13}-3.\, 899\,3\times 10^{12}i \\ -5.\, 864\,5\times 10^{12}+9.\, 764\,2\times 10^{12}i \\ -1.\, 562\,9\times 10^{13}+3.\, 899\,9\times 10^{12}i \end{array} \right]\nonumber$$ Тепер розділіть на запис, щоб вектор мав розумний розмір. Це дає $$\left[ \begin{array}{c} -0.999\,99-3.\, 614\,0\times 10^{-5}i \\ 0.499\,99-0.499\,99i \\ 1.0 \end{array} \right]\nonumber$$ , який близький до $$\left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right]\nonumber$$ Тоді $$\left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right] \left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right] =\left[ \begin{array}{c} -1.0-1.0i \\ 1.0 \\ 1.0+1.0i \end{array} \right]\nonumber$$ Тепер, щоб визначити власне значення, ви можете просто взяти співвідношення відповідних записів. Виберіть два відповідні записи, які мають найбільші абсолютні значення. У цьому випадку ви отримаєте власне значення,$1+i$ яке трапляється бути точним власним значенням. Таким чином, власним вектором і власним значенням є $$\left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right], 1+i\nonumber$$

Зазвичай це не вийде так добре, але ви все одно можете знайти те, що бажане. Таким чином, як тільки ви отримали приблизні власні значення за допомогою$QR$ алгоритму, ви зможете знайти власне значення більш точно разом з власним вектором, пов'язаним з ним, використовуючи метод зсунутої зворотної потужності.

Квадратичні форми

Одним із застосувань ортогональної діагоналізації є квадратичні форми та графіки кривих рівня квадратичної форми. Цей розділ пов'язаний з обертанням осей так, що щодо нових осей графік кривої рівня квадратичної форми орієнтований паралельно осям координат. Це значно полегшує розуміння. Наприклад, ми всі знаємо, що$x_1^2 + x_2^2=1$ представляє рівняння в двох змінних, граф яких в$\mathbb{R}^2$ є окружністю радіуса$1$. Але як ми знаємо, що$5x_1^2 + 4x_1x_2 + 3x_2^2=1$ являє собою графік рівняння?

Спочатку формально визначаємо, що мається на увазі під квадратичною формою. У цьому розділі ми будемо працювати тільки з реальними квадратичними формами, а це значить, що коефіцієнти все будуть дійсними числами.

Визначення$\PageIndex{8}$: Quadratic Form

Квадратична форма - це многочлен ступеня два в$n$ змінних$x_1, x_2, \cdots, x_n$, записаний у вигляді лінійної комбінації$x_i^{2}$$x_ix_j$ термінів і членів.

Розглянемо квадратичну форму$q = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2 + \cdots$. Ми можемо записати$\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]$ як вектор, чиї записи є змінними, що містяться в квадратичній формі.

Аналогічно, нехай$A = \left[ \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right]$ буде матриця, чиї записи є коефіцієнтами$x_i^2$ і$x_ix_j$ від$q$. Відзначимо, що матриця не$A$ є унікальною, і ми розглянемо це далі в прикладі нижче. Використовуючи цю матрицю$A$, квадратичну форму можна записати як$q = \vec{x}^T A \vec{x}$.

$$\begin{aligned} q &= \vec{x}^T A \vec{x} \\ &= \left[ \begin{array}{rrrr} x_1 & x_2 & \cdots & x_n \end{array} \right] \left[ \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] \\ &= \left[ \begin{array}{rrrr} x_1 & x_2 & \cdots & x_n \end{array} \right] \left[ \begin{array}{c} a_{11}x_1 + a_{21}x_2 + \cdots + a_{n1}x_n \\ a_{12}x_1 + a_{22}x_2 + \cdots + a_{n2}x_n \\ \vdots \\ a_{1n}x_1 + a_{2n}x_2 + \cdots + a_{nn}x_n \end{array} \right] \\ &= a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2 + \cdots\end{aligned}$$

Давайте вивчимо, як знайти цю матрицю$A$. Розглянемо наступний приклад.

Приклад$\PageIndex{13}$: Matrix of a Quadratic Form

Нехай квадратичну форму$q$ задано $$q = 6x_1^2 + 4x_1x_2 + 3x_2^2\nonumber$$ Write$q$ у формі$\vec{x}^TA\vec{x}$.

Рішення

По-перше, нехай$\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]$ і$A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]$.

Потім, писемність$q = \vec{x}^TA\vec{x}$ дає $$\begin{aligned} q &= \left[ \begin{array}{rr} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right] \\ &= a_{11}x_1^2 + a_{21}x_1x_2 + a_{12}x_1x_2 + a_{22}x_2^2\end{aligned}$$

Зверніть увагу, що у нас є$x_1x_2$ термін, а також$x_2x_1$ термін. Оскільки множення є комутативним, ці терміни можна комбінувати. Це означає, що$q$ можна написати $$q = a_{11}x_1^2 + \left( a_{21}+ a_{12}\right) x_1x_2 + a_{22}x_2^2\nonumber$$

Прирівнюючи це до того,$q$ як наведено в прикладі, ми маємо $$a_{11}x_1^2 + \left( a_{21}+ a_{12}\right) x_1x_2 + a_{22}x_2^2 = 6x_1^2 + 4x_1x_2 + 3x_2^2\nonumber$$

Тому, $$\begin{aligned} a_{11} &= 6 \\ a_{22} &= 3 \\ a_{21}+a_{12} &= 4\end{aligned}$$

Це свідчить про те, що матриця не$A$ є унікальною, так як існує кілька правильних рішень$a_{21}+a_{12} = 4$. Однак ми завжди будемо вибирати коефіцієнти такі, що$a_{21} = a_{12} = \frac{1}{2} (a_{21}+a_{12})$. Це призводить до$a_{21} = a_{12} = 2$. Цей вибір є ключовим, так як буде гарантувати, що$A$ вийде симетрична матриця.

Отже, $$A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] = \left[ \begin{array}{rr} 6 & 2 \\ 2 & 3 \end{array} \right]\nonumber$$

Ви можете перевірити, що$q = \vec{x}^T A \vec{x}$ тримає цей вибір$A$.

Наведена вище процедура вибору$A$ симетричності застосовується для будь-якої квадратичної форми$q$. Ми завжди будемо вибирати коефіцієнти такі, що$a_{ij}=a_{ji}$.

Тепер звернемо увагу на фокус цього розділу. Наша мета - почати з квадратичної форми$q$, наведеної вище, і знайти спосіб переписати її, щоб усунути$x_ix_j$ терміни. Це робиться за допомогою зміни змінних. Іншими словами, ми хочемо знайти$y_i$ таке, що $$q = d_{11}y_1^2 + d_{22}y_2^2 + \cdots + d_{nn}y_n^2\nonumber$$ Дозволяючи$\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]$ і$D = \left[ d_{ij} \right]$, ми можемо записати$q = \vec{y}^T D \vec{y}$ звідки$D$ матриця коефіцієнтів від$q$. У цій матриці є щось особливе$D$, що має вирішальне значення. Оскільки жодних$y_iy_j$ термінів не існує$q$, то випливає, що$d_{ij} = 0$ для всіх$i \neq j$. Тому$D$ є діагональна матриця. Через цю зміну змінних ми знаходимо головні$y_1, y_2, \cdots, y_n$ осі квадратичної форми.

Ця дискусія встановлює основу для наступної істотної теореми.

Теорема$\PageIndex{11}$: Diagonalizing a Quadratic Form

$q$Дозволяти квадратичну форму в змінних$x_1, \cdots, x_n$. Звідси випливає, що$q$ може бути записана в тому вигляді,$q = \vec{x}^T A \vec{x}$ де $$\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]\nonumber$$ і$A = \left[ a_{ij} \right]$ є симетричною матрицею коефіцієнтів$q$.

Нові змінні$y_1, y_2, \cdots, y_n$ можна знайти такі, що$q = \vec{y}^T D \vec{y}$ де $$\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]\nonumber$$ і$D=\left[ d_{ij} \right]$ є діагональною матрицею. Матриця$D$ містить власні значення$A$ і знаходить методом ортогональної діагоналізації$A$.

Хоча це не формальний доказ, наступна дискусія повинна переконати вас у тому, що вищевказана теорема має місце. $q$Дозволяти квадратичну форму в змінних$x_1, \cdots, x_n$. Потім,$q$ можна записати у вигляді$q = \vec{x}^T A \vec{x}$ для симетричної матриці$A$. За теоремою$\PageIndex{3}$ ми можемо ортогонально діагонально діагонально матрицю$A$ таку, що$U^TAU = D$ для ортогональної матриці$U$ та діагональної матриці$D$.

Потім вектор$\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]$ знаходить по$\vec{y} = U^T \vec{x}$. Щоб побачити, що це працює, перепишіть$\vec{y} = U^T \vec{x}$ як$\vec{x} = U\vec{y}$. Відпустивши$q = \vec{x}^TA\vec{x}$, дійте наступним чином: $$\begin{aligned} q &= \vec{x}^T A \vec{x}\\ &= (U\vec{y})^T A (U\vec{y})\\ &= \vec{y}^T (U^TAU) \vec{y} \\ &= \vec{y}^T D \vec{y}\end{aligned}$$

Наступна процедура детально описує кроки зміни змінних, наведених у вищезгаданій теоремі.

Порядок дій$\PageIndex{5}$: Diagonalizing a Quadratic Form

$q$Дозволяти квадратичну форму в змінних,$x_1, \cdots, x_n$ заданих $$q = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2+\cdots\nonumber$$ потім,$q$ може бути записана$q = d_{11}y_1^2 + \cdots + d_{nn}y_n^2$ наступним чином:

1. Запишіть$q = \vec{x}^T A \vec{x}$ для симетричної матриці$A$.
2. Ортогонально$A$ діагонально записуються як$U^TAU=D$ для ортогональної матриці, так$U$ і діагональної матриці$D$.
3. Напишіть$\vec{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]$. Потім,$\vec{x} = U \vec{y}$.
4. Квадратична форма тепер$q$ буде задаватися $$q = d_{11}y_1^2 + \cdots + d_{nn}y_n^2 = \vec{y}^T D \vec{y}\nonumber$$ де$D = \left[ d_{ij} \right]$ діагональна матриця, знайдена ортогонально діагоналлю$A$.

Розглянемо наступний приклад.

Приклад$\PageIndex{14}$: Choosing New Axes to Simplify a Quadratic Form

Розглянемо наступну криву рівня, $$6x_1^2 + 4x_1x_2 + 3x_2^2 = 7\nonumber$$ показану на наступному графіку.

Малюнок$\PageIndex{1}$

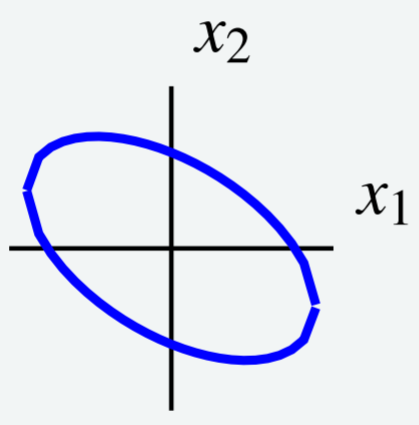
Використовуйте зміну змінних, щоб вибрати нові осі таким чином, щоб еліпс орієнтувався паралельно новим осям координат. Іншими словами, використовуйте зміну змінних для перезапису$q$, щоб усунути$x_1x_2$ термін.

Рішення

Зверніть увагу, що крива рівня задається$q = 7$ для$q = 6x_1^2 + 4x_1x_2 + 3x_2^2$. Це та сама квадратична форма, яку ми розглядали раніше в прикладі$\PageIndex{13}$. Тому ми знаємо, що можемо писати$q = \vec{x}^T A \vec{x}$ для матриці $$A = \left[ \begin{array}{rr} 6 & 2 \\ 2 & 3 \end{array} \right]\nonumber$$

Тепер ми хочемо ортогонально діагонально$A$ писати$U^TAU=D$ для ортогональної матриці$U$ і діагональної матриці$D$. Деталі залишаємо читачеві, і ви можете переконатися, що отримані матриці $$\begin{aligned} U &= \left[ \begin{array}{rr} \frac{2}{\sqrt{5}} & - \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \end{array} \right] \\ D &= \left[ \begin{array}{rr} 7 & 0 \\ 0 & 2 \end{array} \right]\end{aligned}$$

Далі пишемо$\vec{y} = \left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right]$. Звідси випливає, що$\vec{x} = U \vec{y}$.

Тепер ми можемо висловити квадратичну форму з$q$ точки зору$y$, використовуючи записи з$D$ як коефіцієнти наступним чином: $$\begin{aligned} q &= d_{11}y_1^2 + d_{22}y_2^2 \\ &= 7y_1^2 + 2y_2^2 \end{aligned}$$

Звідси крива рівня може бути записана$7y_1^2 + 2y_2^2 =7$. Графік цього рівняння задається:

Малюнок$\PageIndex{2}$

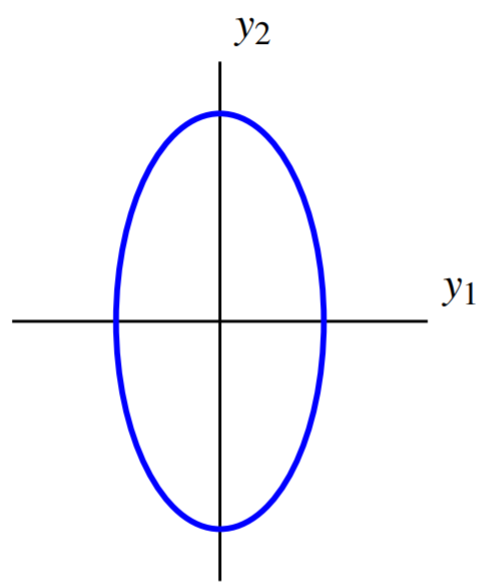
Зміна змінних призводить до нових осей таким чином, що по відношенню до нових осей еліпс орієнтований паралельно осям координат. Вони називаються основними осями квадратичної форми.

Далі наведено ще один приклад діагоналізації квадратичної форми.

Приклад$\PageIndex{15}$: Choosing New Axes to Simplify a Quadratic Form

Розглянемо криву рівня, $$5x_1^{2}-6x_1x_2+5x_2^{2}=8\nonumber$$ показану на наступному графіку.

Малюнок$\PageIndex{3}$

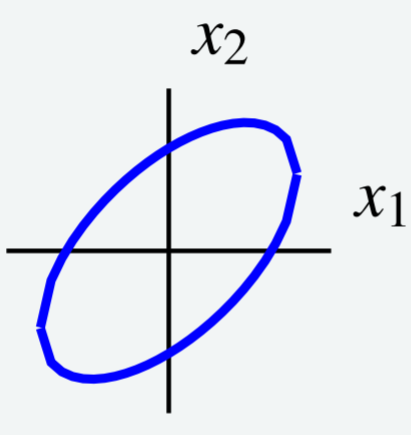
Використовуйте зміну змінних, щоб вибрати нові осі таким чином, щоб еліпс орієнтувався паралельно новим осям координат. Іншими словами, використовуйте зміну змінних для перезапису$q$, щоб усунути$x_1x_2$ термін.

Рішення

По-перше, висловіть криву рівня так,$\vec{x}^TA\vec{x}$ де$\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]$ і$A$ є симетричною. Нехай$A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]$. Потім$q = \vec{x}^T A \vec{x}$ дається $$\begin{aligned} q &= \left[ \begin{array}{cc} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]\\ &= a_{11}x_1^2 + (a_{12} + a_{21})x_1x_2 + a_{22}x_2^2\end{aligned}$$

Прирівнюючи це до даного опису для$q$, ми маємо $$5x_1^2 -6x_1x_2 + 5x_2^2 = a_{11}x_1^2 + (a_{12} + a_{21})x_1x_2 + a_{22}x_2^2\nonumber$$ Це означає, що$a_{11} = 5, a_{22} = 5$ і для того,$A$ щоб бути симетричним,$a_{12} = a_{22} = \frac{1}{2} (a_{12}+a_{21}) = -3$. Результат є$A = \left[ \begin{array}{rr} 5 & -3 \\ -3 & 5 \end{array} \right]$. Ми можемо писати$q = \vec{x}^TA\vec{x}$ як $$\left[ \begin{array}{cc} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} 5 & -3 \\ -3 & 5 \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] =8\nonumber$$

Далі ортогонально діагоналізуємо матрицю$A$ для запису$U^TAU = D$. Деталі залишаються читачеві і необхідні матриці задаються $$\begin{aligned} U &= \left[ \begin{array}{rr} \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \end{array} \right] \\ D &= \left[ \begin{array}{rr} 2 & 0 \\ 0 & 8 \end{array} \right]\end{aligned}$$

Пишіть$\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \end{array} \right]$, такий що$\vec{x} = U \vec{y}$. Потім випливає, що$q$ дається $$\begin{aligned} q &= d_{11}y_1^2 + d_{22}y_2^2 \\ &= 2y_1^{2}+8y_2^{2}\end{aligned}$$ Тому криву рівня можна записати як$2y_1^{2}+8y_2^{2}=8$.

Це еліпс, який паралельний осям координат. Графік його має вигляд

Малюнок$\PageIndex{4}$

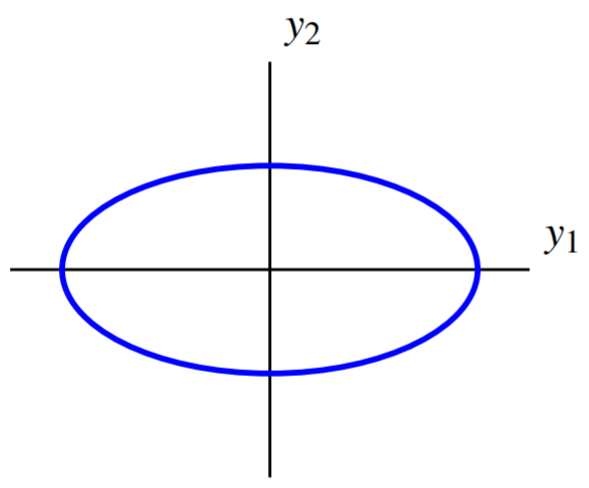
Таким чином, ця зміна змінних вибирає нові осі, такі, що стосовно цих нових осей еліпс орієнтований паралельно осям координат.