4.4: Довжина вектора
- Page ID
- 63133
- Знайти довжину вектора і відстань між двома точками в\(\mathbb{R}^n\).
- Знайти відповідний одиничний вектор вектору в\(\mathbb{R}^n\).
У цьому розділі ми досліджуємо, що мається на увазі під довжиною вектора в\(\mathbb{R}^n\). Ми розробляємо цю концепцію, спочатку подивившись на відстань між двома точками в\(\mathbb{R}^n\).
Спочатку розглянемо поняття відстані для\(\mathbb{R}\), тобто для точок в\(\mathbb{R}^1\). Тут відстань між двома точками\(P\) і\(Q\) задається абсолютним значенням їх різниці. Позначимо відстань між\(P\) і\(Q\) по\(d(P,Q)\) яке визначається як\[d(P,Q) = \sqrt{ \left( P-Q\right) ^{2}} \label{distance1}\]
Розглянемо тепер випадок для\(n=2\), продемонстрований наступною картинкою.
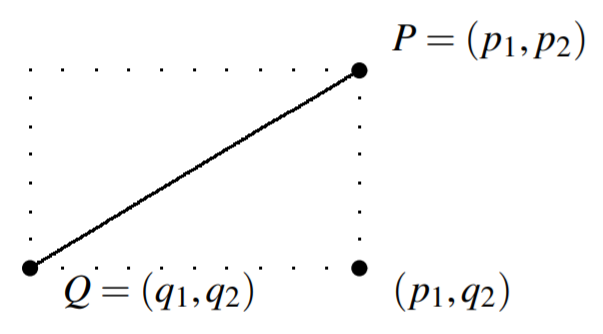
Є дві точки\(P =\left( p_{1},p_{2}\right)\) і\(Q = \left(q_{1},q_{2}\right)\) в площині. Відстань між цими точками показано на малюнку у вигляді суцільної лінії. Зверніть увагу, що ця лінія є гіпотенузою прямокутного трикутника, який є половиною прямокутника, показаного пунктирними лініями. Ми хочемо знайти довжину цієї гіпотенузи, яка дасть відстань між двома точками. Зверніть увагу на довжини сторін цього трикутника\(\left| p_{1}-q_{1}\right|\) і\(\left| p_{2}-q_{2}\right|\), абсолютне значення різниці цих значень. Тому теорема Піфагора має на увазі довжину гіпотенузи (і, таким чином, відстань між\(P\) і\(Q\)) дорівнює\[\left( \left| p_{1}-q_{1}\right| ^{2}+\left| p_{2}-q_{2}\right| ^{2}\right) ^{1/2}=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2} \label{distance2}\]
Тепер припустимо,\(n=3\)\(P = \left( p_{1},p_{2},p_{3}\right)\) і нехай і\(Q = \left( q_{1},q_{2},q_{3}\right)\) бути двома точками в\(\mathbb{R}^{3}.\) Розглянемо наступну картину, в якій суцільна лінія з'єднує дві точки і пунктирна лінія приєднується до точок\(\left( q_{1},q_{2},q_{3}\right)\) і\(\left( p_{1},p_{2},q_{3}\right) .\)
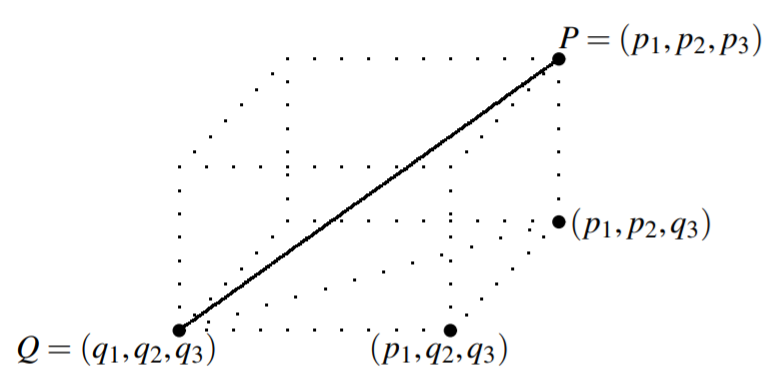
Тут нам потрібно використовувати теорему Піфагора двічі, щоб знайти довжину суцільної лінії. По-перше, за теоремою Піфагора, довжина пунктирної лінії, що з'єднується\(\left( q_{1},q_{2},q_{3}\right)\) і\(\left( p_{1},p_{2},q_{3}\right)\) дорівнює в\[\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\nonumber \] той час як довжина лінії, що\(\left( p_{1},p_{2},p_{3}\right)\) приєднується\(\left( p_{1},p_{2},q_{3}\right)\) до, просто\(\left| p_{3}-q_{3}\right| .\) Тому, за теоремою Піфагора знову, довжина лінії, що з'єднує точки\(P = \left( p_{1},p_{2},p_{3}\right)\) і \(Q = \left( q_{1},q_{2},q_{3}\right)\)дорівнює\[\left( \left( \left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2}\nonumber \]\[=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2} \label{distance3}\]
Ця дискусія мотивує наступне визначення відстані між точками в\(\mathbb{R}^n\).
\(P=\left( p_{1},\cdots ,p_{n}\right)\)\(Q=\left( q_{1},\cdots ,q_{n}\right)\)Дозволяти і бути дві точки в\(\mathbb{R}^{n}\). Тоді відстань між цими точками визначається як\[\text{ distance between }P\text{ and } Q\text{ } = d( P, Q ) = \left( \sum_{k=1}^{n}\left\vert p_{k}-q_{k}\right\vert ^{2}\right) ^{1/2}\nonumber \] Це називається формулою відстані. Ми також можемо записати\(\left\vert P - Q \right\vert\) як відстань між\(P\) і\(Q\).
З наведеного вище обговорення видно, що визначення\(\PageIndex{1}\) має місце для особливих випадків\(n=1,2,3\), як у рівняннях\(\eqref{distance1}\)\(\eqref{distance2}\),\(\eqref{distance3}\). У наступному прикладі ми використовуємо Definition,\(\PageIndex{1}\) щоб знайти відстань між двома точками в\(\mathbb{R}^4\).
Знайти відстань між точками\(P\) і\(Q\) в\(\mathbb{R}^{4}\), де\(P\) і\(Q\) задані\[P=\left( 1,2,-4,6\right)\nonumber \] і\[Q=\left( 2,3,-1,0\right)\nonumber \]
Рішення
Ми будемо використовувати формулу, наведену в Definition, \(\PageIndex{1}\)щоб знайти відстань між\(P\) і\(Q\). Скористайтеся формулою відстані і запишіть\[d(P,Q)= \left( \left( 1-2\right) ^{2}+\left( 2-3\right) ^{2}+\left( -4-\left( -1\right) \right) ^{2}+\left( 6-0\right)^{2}\right) ^{\frac{1}{2}} = 47\nonumber \]
Тому,\(d( P,Q) = \sqrt{47}.\)
Існують певні властивості відстані між точками, які важливі в нашому дослідженні. Вони викладені в наступній теоремі.
Дозволяти\(P\) і\(Q\) бути точки в\(\mathbb{R}^n\), і нехай відстань між ними\(d( P, Q)\), буде дано, як у визначенні\(\PageIndex{1}\). Потім наступні властивості утримують.
- \(d( P, Q) = d( Q, P)\)
- \(d( P, Q) \geq 0\), і дорівнює 0 саме тоді, коли\(P = Q.\)
Існує багато застосувань поняття відстані. Наприклад, з огляду на два пункти, ми можемо запитати, яка колекція балів - це однакова відстань між заданими точками. Це досліджується в наступному прикладі.
Опишіть точки\(\mathbb{R}^3\), в яких знаходяться на однаковій відстані між\(\left( 1,2,3\right)\) і\(\left( 0,1,2\right) .\)
Рішення
Нехай\(P = \left( p_1 , p_2, p_3\right)\) буде такий момент. Тому\(P\) однакова відстань від\(\left( 1,2,3\right)\) і\(\left( 0,1,2\right) .\) тоді за визначенням \(\PageIndex{1}\),\[\sqrt{\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3-3\right) ^{2}}= \sqrt{\left( p_1 - 0 \right)^{2}+\left( p_2-1\right) ^{2}+\left( p_3-2\right) ^{2}}\nonumber \] Квадратуючи обидві сторони ми отримуємо\[\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3 -3\right) ^{2}=p_1^{2}+\left( p_2-1\right) ^{2}+\left( p_3 -2\right) ^{2}\nonumber \] і так\[ \ p_1^{2}-2p_1+14+p_2^{2}-4p_2+p_3^{2}-6p_3=p_1^{2}+p_2^{2}-2p_2+5+p_3^{2}-4p_3\nonumber \] спрощуючи, це стає\[-2p_1+14-4p_2-6p_3=-2p_2+5-4p_3\nonumber \] що можна записати як\[2p_1+2p_2+2p_3=-9 \label{distanceplane}\] Отже, точки \(P = \left( p_1,p_2,p_3\right)\)які однакові відстані від кожної з заданих точок утворюють площину, рівняння якої задається\(\eqref{distanceplane}\).
Тепер ми можемо використовувати наше розуміння відстані між двома точками, щоб визначити, що мається на увазі під довжиною вектора. Розглянемо наступне визначення.
\(\vec{u} = \left[ u_{1} \cdots u_{n} \right]^T\)Дозволяти бути вектор в\(\mathbb{R}^n\). Потім довжина\(\vec{u}\), написана\(\| \vec{u} \|\) задається\[\| \vec{u} \| = \sqrt{ u_{1}^2 + \cdots + u_{n}^2}\nonumber \]
Це визначення відповідає Визначенню\(\PageIndex{1}\), якщо врахувати, що вектор\(\vec{u}\) має хвіст у точці,\(0 = \left( 0, \cdots ,0 \right)\) а кінчик - у точці\(U = \left(u_1, \cdots, u_n \right)\). Тоді довжина\(\vec{u}\) дорівнює відстані між\(0\) і\(U\),\(d(0,U)\). Загалом,\(d(P,Q)=||\vec{PQ}||\).
Розглянемо приклад \(\PageIndex{1}\). За визначенням \(\PageIndex{2}\), ми також могли б знайти відстань між\(P\) і\(Q\) як довжину вектора, що з'єднує їх. Отже, якби ми намалювали вектор\(\overrightarrow{PQ}\) з хвостом в\(P\) і його точці в\(Q\), цей вектор мав би довжину рівну\(\sqrt{47}\).
Завершується цей розділ новим визначенням для окремого випадку векторів довжини\(1\).
\(\vec{u}\)Дозволяти бути вектор в\(\mathbb{R}^{n}\). Потім ми\(\vec{u}\) називаємо вектор одиниці, якщо він має довжину 1, тобто якщо\[\| \vec{u} \| = 1\nonumber \]
\(\vec{v}\)Дозволяти бути вектор в\(\mathbb{R}^{n}\). Потім вектор,\(\vec{u}\) який має той самий напрямок, що і довжина\(\vec{v}\) дорівнює,\(1\) є відповідним одиничним вектором\(\vec{v}\). Цей вектор задається\[\vec{u} = \frac{1}{\| \vec{v} \|} \vec{v}\nonumber \]
Ми часто використовуємо термін нормалізувати для позначення цього процесу. Коли ми нормалізуємо вектор, знаходимо відповідний одиничний вектор довжини\(1\). Розглянемо наступний приклад.
\(\vec{v}\)Дозволяти задається\[\vec{v} = \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T\nonumber \] знахідкою вектора одиниці\(\vec{u}\), який має той самий напрямок, що і\(\vec{v}\).
Рішення
Ми будемо використовувати Definition\(\PageIndex{3}\), щоб вирішити цю проблему. Тому нам потрібно знайти довжину\(\vec{v}\) якої, за визначенням\(\PageIndex{2}\) задається за\[\| \vec{v} \| = \sqrt{ v_{1}^2 + v_{2}^2+ v_{3}^2}\nonumber \] допомогою відповідних значень ми знаходимо, що Для\[\begin{aligned} \| \vec{v} \| &= \sqrt{ 1^2 + \left(-3 \right)^2 + 4^2} \\ &= \sqrt{ 1 + 9 + 16} \\ &= \sqrt{26} \end{aligned}\] того, щоб знайти\(\vec{u}\), ми ділимо\(\vec{v}\) на\(\sqrt{26}\). Результат -\[\begin{aligned} \vec{u} &= \frac{1}{\| \vec{v} \|} \vec{v} \\ &= \frac{1}{\sqrt{26}} \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T \\ &= \left[ \begin{array}{rrr} \frac{1}{\sqrt{26}} & -\frac{3}{\sqrt{26}} & \frac{4}{\sqrt{26}} \end{array} \right]^T\end{aligned}\]
Ви можете перевірити, використовуючи Визначення\(\PageIndex{1}\), що\(\| \vec{u} \| = 1\).
