1.9: Вправи
- Page ID
- 63196
Вправи
Графічно знайдіть точку,\(\left( x_{1},y_{1}\right)\) яка лежить на обох лініях,\(x+3y=1\) і\(4x-y=3.\) Тобто прорисуйте кожну лінію і подивіться, де вони перетинаються.
- Відповідь
-
\(\begin{array}{c} x+3y=1 \\ 4x-y=3 \end{array}\), Рішення є:\(\left[ x=\frac{10}{13},y=\frac{1}{13}\right]\).
Графічно знайдіть точку перетину двох ліній\(3x+y=3\) і\(x+2y=1.\) Тобто намалюйте кожну пряму і подивіться, де вони перетинаються.
- Відповідь
-
\(\begin{array}{c} 3x+y=3 \\ x+2y=1 \end{array}\), Рішення є:\(\left[ x=1,y=0\right]\)
Чи три лінії,,\(x + 2y = 1\)\(2x − y = 1\), і\(4x + 3y = 3\) мають спільну точку перетину? Якщо так, знайдіть точку, а якщо ні, скажіть, чому вони не мають такої спільної точки перетину.
- Відповідь
-
\(\begin{array}{c}x+2y=1 \\ 2x-y=1\\4x+3y=3\end{array}\), Рішення полягає в:\(\left[ x=\frac{3}{5},y=\frac{1}{5}\right]\)
Чи три площини,\(x+y−3z = 2\),\(2x+y+z = 1\), і\(3x+2y−2z = 0\) мають спільну точку перетину? Якщо так, знайдіть його, а якщо ні, скажіть, чому немає такого пункту.
- Відповідь
-
Рішення не існує. Ви можете переконатися в цьому, написавши розширену матрицю і виконуючи операції з рядками. \(\left[\begin{array}{cccc}1&1&-3&2 \\ 2&1&1&1 \\ 3&2&-2&0\end{array}\right]\), Ряд ешелону форми:\(\left[\begin{array}{cccc}1&0&4&0 \\ 0&1&-7&0 \\ 0&0&0&1\end{array}\right]\). Таким чином, одне з рівнянь говорить\(0=1\) в еквівалентній системі рівнянь.
У чотири рази вага Гастона на\(150\) кілограми більше, ніж вага Ікабода. У чотири рази вага Ікабода становить\(660\) кілограми менше, ніж у сімнадцять разів перевищує вагу Гастона. Чотири рази вага Гастона плюс вага Зігфріда дорівнює\(290\) фунтам. Брунхільда врівноважувала б усіх трьох інших. Знайдіть ваги чотирьох людей.
- Відповідь
-
\(\begin{array}{c}4g-I=150 \\ 4I-17g=-660 \\ 4g+s=290 \\ g+I+s-b=0\end{array}\), Рішення полягає в:\(\left\{ g=60, I=90, b=200, s=50\right\}\)
Розглянемо наступну доповнену матрицю, в якій\(\ast\) позначається довільне число і\(\blacksquare\) позначає ненульове число. Визначте, чи відповідає дана доповнена матриця. Якщо послідовно, чи є рішення унікальним? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast & 0 & \ast \\ 0 & 0 & \blacksquare & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
- Відповідь
-
Рішення існує, але не є унікальним.
Розглянемо наступну доповнену матрицю, в якій\(\ast\) позначається довільне число і\(\blacksquare\) позначає ненульове число. Визначте, чи відповідає дана доповнена матриця. Якщо послідовно, чи є рішення унікальним? \[\left[ \begin{array}{ccc|c} \blacksquare & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast \\ 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
- Відповідь
-
Рішення існує і є унікальним.
Розглянемо наступну доповнену матрицю, в якій\(\ast\) позначається довільне число і\(\blacksquare\) позначає ненульове число. Визначте, чи відповідає дана доповнена матриця. Якщо послідовно, чи є рішення унікальним? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & 0 & \ast & 0 & \ast \\ 0 & 0 & 0 & \blacksquare & \ast & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
Розглянемо наступну доповнену матрицю, в якій\(\ast\) позначається довільне число і\(\blacksquare\) позначає ненульове число. Визначте, чи відповідає дана доповнена матриця. Якщо послідовно, чи є рішення унікальним? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast & 0 & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & 0 \\ 0 & 0 & 0 & 0 & \ast & \blacksquare \end{array} \right]\nonumber \]
- Відповідь
-
Може бути рішення. Якщо так, то їх нескінченно багато.
Припустимо, система рівнянь має менше рівнянь, ніж змінних. Чи обов'язково така система буде послідовною? Якщо так, поясніть, чому, а якщо ні, наведіть приклад, який не є послідовним.
- Відповідь
-
Ні. Розглянемо\(x+y+z=2\) і\(x+y+z=1.\)
Якщо система рівнянь має більше рівнянь, ніж змінних, чи може вона мати рішення? Якщо так, наведіть приклад, а якщо ні, скажіть, чому б і ні.
- Відповідь
-
Вони можуть мати рішення. Наприклад,\(x+y=1,2x+2y=2,3x+3y=3\) навіть має нескінченний набір рішень.
Знайдіть\(h\) такі, що\[\left[ \begin{array}{rr|r} 2 & h & 4 \\ 3 & 6 & 7 \end{array} \right]\nonumber \] є доповненою матрицею неузгодженої системи.
- Відповідь
-
\(h=4\)
Знайдіть\(h\) такі, що\[\left[ \begin{array}{rr|r} 1 & h & 3 \\ 2 & 4 & 6 \end{array} \right]\nonumber \] є доповненою матрицею послідовної системи.
- Відповідь
-
Будь-яка\(h\) буде працювати.
Знайдіть\(h\) такі, що\[\left[ \begin{array}{rr|r} 1 & 1 & 4 \\ 3 & h & 12 \end{array} \right]\nonumber \] є доповненою матрицею послідовної системи.
- Відповідь
-
Будь-яка\(h\) буде працювати.
Виберіть\(h\) і\(k\) такі, щоб показана розширена матриця мала кожне з наступних:
- одне рішення
- немає рішення
- нескінченно багато рішень
\[\left[ \begin{array}{rr|r} 1 & h & 2 \\ 2 & 4 & k \end{array} \right]\nonumber \]
- Відповідь
-
Якщо\(h\neq 2\) буде унікальне рішення для будь-якого\(k\). Якщо\(h=2\) і\(k\neq 4,\) немає рішень. Якщо\(h=2\) і\(k=4,\) то існує нескінченно багато рішень.
Виберіть\(h\) і\(k\) такі, щоб показана розширена матриця мала кожне з наступних:
- одне рішення
- немає рішення
- нескінченно багато рішень
\[\left[ \begin{array}{rr|r} 1 & 2 & 2 \\ 2 & h & k \end{array} \right]\nonumber \]
- Відповідь
-
Якщо\(h\neq 4,\) тоді є рівно одне рішення. Якщо\(h=4\) і\(k\neq 4,\) тоді рішень немає. Якщо\(h=4\) і\(k=4,\) то існує нескінченно багато рішень.
Визначте, чи послідовна система. Якщо так, то чи унікальне рішення? \[\begin{array}{c} x+2y+z-w=2 \\ x-y+z+w=1 \\ 2x+y-z=1 \\ 4x+2y+z=5 \end{array}\nonumber \]
- Відповідь
-
Рішення немає. Система непослідовна. Ви можете побачити це з доповненої матриці. \(\left[ \begin{array}{rrrrr} 1 & 2 & 1 & -1 & 2 \\ 1 & -1 & 1 & 1 & 1 \\ 2 & 1 & -1 & 0 & 1 \\ 4 & 2 & 1 & 0 & 5 \end{array} \right]\), Зменшена рядно-ешелонна форма:\(\left[ \begin{array}{rrrrr} 1 & 0 & 0 & \frac{1}{3} & 0 \\ 0 & 1 & 0 & -\frac{2}{3} & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right] .\)
Визначте, чи послідовна система. Якщо так, то чи унікальне рішення? \[\begin{array}{c} x+2y+z-w=2 \\ x-y+z+w=0 \\ 2x+y-z=1 \\ 4x+2y+z=3 \end{array}\nonumber \]
- Відповідь
-
Рішення полягає в:\(\left[ w=\frac{3}{2}y-1,x=\frac{2}{3}-\frac{1}{2}y,z=\frac{1}{3 }\right]\)
Визначте, які матриці знаходяться в скороченому рядно-ешелоновій формі.
- \(\left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 1 & 7 \end{array} \right]\)
- \(\left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array} \right]\)
- \(\left[ \begin{array}{rrrrrr} 1 & 1 & 0 & 0 & 0 & 5 \\ 0 & 0 & 1 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 & 1 & 3 \end{array} \right]\)
- Відповідь
-
- Це не так.
- Це один.
- Це один.
Рядок зменшуємо наступну матрицю, щоб отримати рядно-ешелонову форму. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 2 & -1 & 3 & -1 \\ 1 & 0 & 2 & 1 \\ 1 & -1 & 1 & -2 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю, щоб отримати рядно-ешелонову форму. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & -1 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю, щоб отримати рядно-ешелонову форму. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 3 & -6 & -7 & -8 \\ 1 & -2 & -2 & -2 \\ 1 & -2 & -3 & -4 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю, щоб отримати рядно-ешелонову форму. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 2 & 4 & 5 & 15 \\ 1 & 2 & 3 & 9 \\ 1 & 2 & 2 & 6 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю для отримання рядно-ешелонової форми. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 4 & -1 & 7 & 10 \\ 1 & 0 & 3 & 3 \\ 1 & -1 & -2 & 1 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю для отримання рядно-ешелонової форми. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} 3 & 5 & -4 & 2 \\ 1 & 2 & -1 & 1 \\ 1 & 1 & -2 & 0 \end{array} \right]\nonumber \]
Рядок зменшуємо наступну матрицю для отримання рядно-ешелонової форми. Потім продовжують отримувати зменшену рядно-ешелонову форму. \[\left[ \begin{array}{rrrr} -2 & 3 & -8 & 7 \\ 1 & -2 & 5 & -5 \\ 1 & -3 & 7 & -8 \end{array} \right]\nonumber \]
Знайдіть рішення системи, доповнена матриця якої\[\left[ \begin{array}{rrr|r} 1 & 2 & 0 & 2 \\ 1 & 3 & 4 & 2 \\ 1 & 0 & 2 & 1 \end{array} \right]\nonumber \]
Знайдіть рішення системи, доповнена матриця якої\[\left[ \begin{array}{rrr|r} 1 & 2 & 0 & 2 \\ 2 & 0 & 1 & 1 \\ 3 & 2 & 1 & 3 \end{array} \right]\nonumber \]
- Відповідь
-
Зменшена рядно-ешелонова форма є\(\left[ \begin{array}{rrr|r} 1 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 1 & -\frac{1}{4} &\frac{3}{4} \\ 0 & 0 & 0 & 0 \end{array} \right] .\) Отже, рішення має форму\(z=t,y=\frac{3}{4}+t\left( \frac{1}{4}\right) ,x=\frac{1}{2}-\frac{1}{2}t\) де\(t\in \mathbb{R}\).
Знайдіть рішення системи, доповнена матриця якої\[\left[ \begin{array}{rrr|r} 1 & 1 & 0 & 1 \\ 1 & 0 & 4 & 2 \end{array} \right]\nonumber \]
- Відповідь
-
Зменшена форма ряду-ешелону - це\(\left[ \begin{array}{rrr|r} 1 & 0 & 4 & 2 \\ 0 & 1 & -4 & -1 \end{array} \right]\) і так рішення\(z=t,y=4t,x=2-4t.\)
Знайдіть рішення системи, доповнена матриця якої\[\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 1 & 2 & 0 & 0 & 1 & 3 \\ 1 & 0 & 1 & 0 & 2 & 2 \end{array} \right]\nonumber \]
- Відповідь
-
Зменшена рядно-ешелонна форма є\(\left[ \begin{array}{rrrrr|r} 1 & 0 & 0 & 0 & 9 & 3 \\ 0 & 1 & 0 & 0 & -4 & 0 \\ 0 & 0 & 1 & 0 & -7 & -1 \\ 0 & 0 & 0 & 1 & 6 & 1 \end{array} \right]\) і так\(x_{5}=t,x_{4}=1-6t,x_{3}=-1+7t,x_{2}=4t,x_{1}=3-9t\).
Знайдіть рішення системи, доповнена матриця якої\[\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 0 & 2 & 0 & 0 & 1 & 3 \\ 1 & -1 & 2 & 2 & 2 & 0 \end{array} \right]\nonumber \]
- Відповідь
-
Зменшена рядно-ешелонна форма є\(\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 0 & -\frac{1}{2} & \frac{5}{2} \\ 0 & 1 & 0 & 0 & \frac{1}{2} & \frac{3}{2} \\ 0 & 0 & 0 & 1 & \frac{3}{2} & -\frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right]\). Тому нехай\(x_{5}=t,x_{3}=s.\) Тоді інші змінні задаються\(x_{4}=-\frac{1}{2}-\frac{3}{2}t,x_{2}=\frac{3}{2}-t\frac{1}{2} ,,x_{1}=\frac{5}{2}+\frac{1}{2}t-2s.\)
Знайти рішення системи рівнянь,\(7x+14y+15z=22,\)\(2x+4y+3z=5,\) і\(3x+6y+10z=13.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=1-2t,z=1,y=t\right]\)
Знайти рішення системи рівнянь,\(3x-y+4z=6,\)\(y+8z=0,\) і\(-2x+y=-4.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=2-4t,y=-8t,z=t\right]\)
Знайти рішення системи рівнянь,\(9x-2y+4z=-17,\)\(13x-3y+6z=-25,\) і\(-2x-z=3.\)
- Відповідь
-
Рішення полягає в:\(\left[x=-1,y=2,z=-1\right]\)
Знайти розв'язку системи рівнянь,\(65x+84y+16z=546,\)\(81x+105y+20z=682,\) і\(84x+110y+21z=713.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=2,y=4,z=5\right]\)
Знайти рішення системи рівнянь,\(8x+2y+3z=-3,8x+3y+3z=-1,\) і\(4x+y+3z=-9.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=1,y=2,z=-5\right]\)
Знайти рішення системи рівнянь,\(-8x+2y+5z=18,-8x+3y+5z=13,\) і\(-4x+y+5z=19.\)
- Відповідь
-
Рішення полягає в:\(\left[x=-1,y=-5,z=4\right]\)
Знайти розв'язку системи рівнянь,\(3x-y-2z=3,\)\(y-4z=0,\) і\(-2x+y=-2.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=2t+1,y=4t,z=t\right]\)
Знайти рішення системи рівнянь,\(-9x+15y=66,-11x+18y=79\),\(-x+y=4\), і\(z=3\).
- Відповідь
-
Рішення полягає в:\(\left[x=1,y=5,z=3\right]\)
Знайти рішення системи рівнянь,\(-19x+8y=-108,\)\(-71x+30y=-404,\)\(-2x+y=-12,\)\(4x+z=14.\)
- Відповідь
-
Рішення полягає в:\(\left[ x=4,y=-4,z=-2\right]\)
Припустимо, система рівнянь має менше рівнянь, ніж змінних, і ви знайшли рішення цієї системи рівнянь. Чи можливо, що ваше рішення єдине? Поясніть.
- Відповідь
-
Ні. Розглянемо\(x+y+z=2\) і\(x+y+z=1.\)
Припустимо, система лінійних рівнянь має\(2\times 4\) доповнену матрицю, а останній стовпець - шарнірну колонку. Чи може система лінійних рівнянь бути послідовною? Поясніть.
- Відповідь
-
Ні. Це призвело б до\(0=1.\)
Припустимо, матриця коефіцієнтів системи\(n\) рівнянь зі\(n\) змінними має властивість, що кожен стовпець є поворотним стовпчиком. Чи випливає, що система рівнянь повинна мати рішення? Якщо так, чи має рішення бути унікальним? Поясніть.
- Відповідь
-
Так. Має унікальне рішення.
Припустимо, існує унікальне рішення системи лінійних рівнянь. Що повинно бути правдою щодо поворотних стовпців у доповненій матриці?
- Відповідь
-
Останній стовпець не повинен бути шарнірною колоною. Решта стовпчиків кожен повинен бути шарнірними стовпчиками.
Температура стійкого стану пластини вирішує рівняння Лапласа,\(\Delta u=0.\) Один із способів наближення рішення полягає в тому, щоб розділити пластину на квадратну сітку і вимагати, щоб температура на кожному вузлі дорівнювала середньому температурі на чотирьох сусідніх вузлах.\(u\) На наступній картинці цифри представляють спостережувану температуру в зазначених вузлах. Знайти температуру на внутрішніх вузлах, позначену\(x,y,z,\) і\(w\). Одним з рівнянь є\(z={0.05in}\frac{1}{4}\left( 10+0+w+x\right)\).
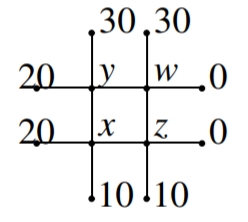
- Відповідь
-
Вам потрібно\(\begin{array}{c} \frac{1}{4}\left( 20+30+w+x\right) -y=0 \\ \frac{1}{4}\left( y+30+0+z\right) -w=0 \\ \frac{1}{4}\left( 20+y+z+10\right) -x=0 \\ \frac{1}{4}\left( x+w+0+10\right) -z=0 \end{array}\), Рішення це:\(\left[ w=15,x=15,y=20,z=10\right] .\)
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrr} 4 & -16 & -1 & -5 \\ 1 & -4 & 0 & -1 \\ 1 & -4 & -1 & -2 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrr} 3 & 6 & 5 & 12 \\ 1 & 2 & 2 & 5 \\ 1 & 2 & 1 & 2 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} 0 & 0 & -1 & 0 & 3 \\ 1 & 4 & 1 & 0 & -8 \\ 1 & 4 & 0 & 1 & 2 \\ -1 & -4 & 0 & -1 & -2 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrr} 4 & -4 & 3 & -9 \\ 1 & -1 & 1 & -2 \\ 1 & -1 & 0 & -3 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} 2 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 7 \\ 1 & 0 & 0 & 1 & 7 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrr} 4 & 15 & 29 \\ 1 & 4 & 8 \\ 1 & 3 & 5 \\ 3 & 9 & 15 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} 0 & 0 & -1 & 0 & 1 \\ 1 & 2 & 3 & -2 & -18 \\ 1 & 2 & 2 & -1 & -11 \\ -1 & -2 & -2 & 1 & 11 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} 1 & -2 & 0 & 3 & 11 \\ 1 & -2 & 0 & 4 & 15 \\ 1 & -2 & 0 & 3 & 11 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrr} -2 & -3 & -2 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ -3 & 0 & -3 \end{array} \right]\nonumber \]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} 4 & 4 & 20 & -1 & 17 \\ 1 & 1 & 5 & 0 & 5 \\ 1 & 1 & 5 & -1 & 2 \\ 3 & 3 & 15 & -3 & 6 \end{array} \right]\nonumber\]
Знайдіть ранг наступної матриці. \[\left[ \begin{array}{rrrrr} -1 & 3 & 4 & -3 & 8 \\ 1 & -3 & -4 & 2 & -5 \\ 1 & -3 & -4 & 1 & -2 \\ -2 & 6 & 8 & -2 & 4 \end{array} \right]\nonumber\]
Припустимо,\(A\) це\(m\times n\) матриця. Поясніть, чому ранг завжди не більше\(A\)\(\min \left( m,n\right) .\)
- Відповідь
-
Це тому, що ви не можете мати більше\(\min \left( m,n\right)\) ненульових рядків у формі зменшеного рядка ешелону. Нагадаємо, що кількість шарнірних стовпчиків таке ж, як і кількість ненульових рядків з опису цієї зменшеної строково-ешелонової форми.
Вкажіть, чи можливі кожний з наступних наборів даних для матричного рівняння\(AX=B\). Якщо є можливість, опишіть набір рішень. Тобто скажіть, чи існує унікальне рішення, немає рішення або нескінченно багато рішень. Тут\(\left[ A |B \right]\) позначає доповнену матрицю.
- \(A\)є\(5\times 6\) матрицею,\(rank\left( A\right) =4\) і\(rank\left[ A|B \right] =4.\)
- \(A\)є\(3\times 4\) матрицею,\(rank\left( A\right) =3\) і\(rank\left[ A|B\right] =2.\)
- \(A\)є\(4\times 2\) матрицею,\(rank\left( A\right) =4\) і\(rank\left[ A|B \right] =4.\)
- \(A\)є\(5\times 5\) матрицею,\(rank\left( A\right) =4\) і\(rank\left[ A|B \right] =5.\)
- \(A\)являє собою\(4\times 2\) матрицю,\(rank\left( A\right) =2\) і\(rank\left[ A|B \right] =2\).
- Відповідь
-
- Це говорить\(B\) знаходиться в прольоті чотирьох колон. При цьому колони не є самостійними. Нескінченний набір рішень.
- Цього, безумовно, не може статися. Якщо додати в інший стовпець, ранг не стане менше.
- \(B\)Це говорить, що в прольоті колон і колони повинні бути незалежними. Ви не можете мати ранг рівний 4, якщо у вас є тільки два стовпці.
- \(B\)Це говорить не в прольоті колон. У цьому випадку рішення системи рівнянь, представленої доповненою матрицею, не існує.
- В цьому випадку існує унікальне рішення, так як колони\(A\) є незалежними.
Розглянемо систему\(-5x+2y-z=0\) і\(-5x-2y-z=0.\) Обидва рівняння дорівнюють нулю і так\(-5x+2y-z=-5x-2y-z\), що еквівалентно\(y=0.\) Чи слідує це\(x\) і\(z\) може дорівнювати чомусь? Зверніть увагу\(x=1\), що коли\(z=-4,\) і\(y=0\) підключені до рівнянь, рівняння не рівні\(0\). Чому?
- Відповідь
-
Це не законні операції рядків. Вони не зберігають набір розчину системи.
Збалансуйте наступні хімічні реакції.
- \(KNO_{3}+H_{2}CO_{3}\rightarrow K_{2}CO_{3}+HNO_{3}\)
- \(AgI+Na_{2}S\rightarrow Ag_{2}S+NaI\)
- \(Ba_{3}N_{2}+H_{2}O\rightarrow Ba\left( OH\right) _{2}+NH_{3}\)
- \(CaCl_{2}+Na_{3}PO_{4}\rightarrow Ca_{3}\left( PO_{4}\right) _{2}+NaCl\)
У розділі про безрозмірні змінні було помічено, що\(\rho V^{2}AB\) має одиниці сили. Опишіть систематичний спосіб отримання таких комбінацій змінних, які дадуть щось, що має одиниці сили.
Розглянемо наступну схему з чотирьох контурів.
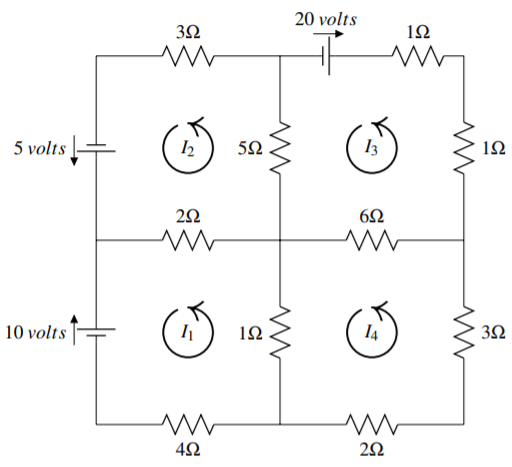
Струм в амперах в чотирьох ланцюгах позначається\(I_{1},I_{2},I_{3},I_{4}\) і мається на увазі, що рух йде в напрямку проти годинникової стрілки. Якщо\(I_{k}\) закінчується негативним, то це просто означає, що струм тече за годинниковою стрілкою.
На наведеній вище схемі верхній лівий ланцюг повинен дати рівняння\[2I_{2}-2I_{1}+5I_{2}-5I_{3}+3I_{2}=5\nonumber \] Для ланцюга зліва внизу ви повинні мати\[4I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}=-10\nonumber \] Записати рівняння для кожного з двох інших ланцюгів, а потім дати рішення отриманої системи рівнянь.
- Відповідь
-
Інші два рівняння\[\begin{aligned} 6I_{3}-6I_{4}+I_{3}+I_{3}+5I_{3}-5I_{2} &=-20 \\ 2I_{4}+3I_{4}+6I_{4}-6I_{3}+I_{4}-I_{1} &=0\end{aligned}\] Тоді система є\[\begin{array}{c} 2I_{2}-2I_{1}+5I_{2}-5I_{3}+3I_{2}=5 \\ 4I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}=-10 \\ 6I_{3}-6I_{4}+I_{3}+I_{3}+5I_{3}-5I_{2}=-20 \\ 2I_{4}+3I_{4}+6I_{4}-6I_{3}+I_{4}-I_{1}=0 \end{array}\nonumber \] Рішення таке:\[\begin{aligned} I_{1}&= -\frac{750}{373} \\ I_{2}&= -\frac{1421}{1119} \\ I_{3}&= -\frac{3061}{1119} \\ I_{4}&= -\frac{1718}{1119}\end{aligned}\]
Розглянемо наступну схему з трьох контурів.
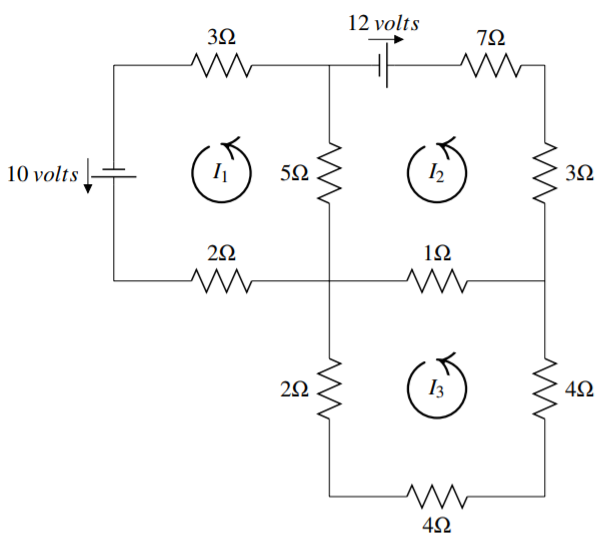
Струм в амперах в чотирьох ланцюгах позначається\(I_{1},I_{2},I_{3}\) і мається на увазі, що рух йде в напрямку проти годинникової стрілки. Якщо\(I_{k}\) закінчується негативним, то це просто означає, що струм тече за годинниковою стрілкою.
Знайти\(I_{1},I_{2},I_{3}\).
- Відповідь
-
У вас є\[\begin{aligned} 2I_{1}+5I_{1}+3I_{1}-5I_{2} &= 10 \\ I_{2}- I_{3} +3I_{2}+7I_{2}+5I_{2}-5I_{1} &=-12 \\ 2I_{3}+4I_{3}+4I_{3}+I_{3}-I_{2} &= 0\end{aligned}\] Спрощення цього дає\[\begin{aligned} 10I_{1}-5I_{2} &= 10 \\ -5I_{1} + 16I_{2}- I_{3} &=-12 \\ -I_{2} + 11I_{3} &=0\end{aligned}\] Рішення дається\[I_{1}=\frac{218}{295},I_{2}=-\frac{154}{295},I_{3}=-\frac{14}{295}\nonumber \]
