5: Система рівнянь

Цілі навчання

Прочитавши цю главу, ви повинні мати можливість:

1. встановлення одночасних лінійних рівнянь у матричній формі і навпаки,
2. зрозуміти поняття зворотної матриці,
3. знати різницю між послідовною і непослідовною системою лінійних рівнянь, і
4. дізнатися, що система лінійних рівнянь може мати унікальне рішення, без розв'язків або нескінченних розв'язків.

Матрична алгебра використовується для розв'язання систем рівнянь. Чи можете ви проілюструвати цю концепцію?

Матрична алгебра використовується для розв'язання системи одночасних лінійних рівнянь. Насправді, для багатьох математичних процедур, таких як розв'язання набору нелінійних рівнянь, інтерполяція, інтеграція та диференціальні рівняння, рішення зводяться до набору одночасних лінійних рівнянь. Проілюструємо на прикладі для інтерполяції.

Приклад 1

Швидкість вгору ракети наведена в три різні часи на наступній таблиці.

Таблиця 5.1. Дані про швидкість проти часу для ракети

Час, т	Швидкість, v
(и)	(м/с)
5	106.8
8	177.2
12	279.2

Дані про швидкість апроксимуються поліномом як

$$v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber$$

Налаштуйте рівняння в матричній формі, щоб знайти$a,b,c$ коефіцієнти профілю швидкостей.

Рішення

Многочлен проходить через три точки даних,$\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),and\left( t_{3},v_{3} \right)$ звідки з таблиці 5.1.

$$t_{1} = 5,\ v_{1} = 106.8 \nonumber$$

$$t_{2} = 8,\ v_{2} = 177.2 \nonumber$$

$$t_{3} = 12,\ v_{3} = 279.2 \nonumber$$

Вимога, що$v\left( t \right) = at^{2} + {bt} + c$ проходить через три точки даних дає

$$v\left( t_{1} \right) = v_{1} = at_{1}^{2} + bt_{1} + c \nonumber$$

$$v\left( t_{2} \right) = v_{2} = at_{2}^{2} + bt_{2} + c \nonumber$$

$$v\left( t_{3} \right) = v_{3} = at_{3}^{2} + bt_{3} + c \nonumber$$

Підстановка даних$\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),\ and\ \left( t_{3},v_{3} \right)$ дає

$$a\left( 5^{2} \right) + b\left( 5 \right) + c = 106.8 \nonumber$$

$$a\left( 8^{2} \right) + b\left( 8 \right) + c = 177.2 \nonumber$$

$$a\left( 12^{2} \right) + b\left( 12 \right) + c = 279.2 \nonumber$$

або

$$25a + 5b + c = 106.8 \nonumber$$

$$64a + 8b + c = 177.2 \nonumber$$

$$144a + 12b + c = 279.2 \nonumber$$

Цей набір рівнянь можна переписати в матричному вигляді як

$$\begin{bmatrix} 25a + & 5b + & c \\ 64a + & 8b + & c \\ 144a + & 12b + & c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Вищевказане рівняння можна записати як лінійну комбінацію наступним чином:

$$a\begin{bmatrix} 25 \\ 64 \\ 144 \\ \end{bmatrix} + b\begin{bmatrix} 5 \\ 8 \\ 12 \\ \end{bmatrix} + c\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

і подальше використання множення матриці дає

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Вище наведено ілюстрацію того, навіщо потрібна матрична алгебра. Повний розв'язок множини рівнянь наведено далі в цьому розділі.

Загальний набір$m$ лінійних рівнянь і$n$ невідомих,

$$a_{11}x_{1} + a_{12}x_{2} + \cdots\cdots + a_{1n}x_{n} = c_{1} \nonumber$$

$$a_{21}x_{1} + a_{22}x_{2} + \cdots\cdots + a_{2n}x_{n} = c_{2} \nonumber$$

$$\text{..........................................} \nonumber$$

$$\text{..........................................} \nonumber$$

$$a_{m1}x_{1} + a_{m2}x_{2} + ........ + a_{mn}x_{n} = c_{m} \nonumber$$

можна переписати в матричному вигляді як

$$\begin{bmatrix} a_{11} & a_{12} & . & . & a_{1n} \\ a_{21} & a_{22} & . & . & a_{2n} \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ a_{m1} & a_{m2} & . & . & a_{mn} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \cdot \\ \cdot \\ x_{n} \\ \end{bmatrix} = \begin{bmatrix} c_{1} \\ c_{2} \\ \cdot \\ \cdot \\ c_{m} \\ \end{bmatrix} \nonumber$$

Позначаючи матриці по$\left\lbrack A \right\rbrack$,$\left\lbrack X \right\rbrack$, і$\left\lbrack C \right\rbrack$, система рівняння дорівнює

$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$, Де$\left\lbrack A \right\rbrack$ називається матрицею коефіцієнтів,$\left\lbrack C \right\rbrack$ називається вектором правого боку і$\left\lbrack X \right\rbrack$ називається вектором рішення.

Іноді$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ системи рівнянь записуються в доповненому вигляді. Тобто

$$\left\lbrack A \ \vdots \ C \right\rbrack = \left\lbrack \begin{matrix} a_{11} & a_{12} & {......} & a_{1n} \\ a_{21} & a_{22} & {......} & a_{2n} \\ \begin{matrix} \vdots \\ \vdots \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} \\ a_{m1} & a_{m2} & {......} & a_{mn} \\ \end{matrix}\begin{matrix} \vdots \\ \vdots \\ \vdots \\ \vdots \\ \vdots \\ \end{matrix}\begin{matrix} c_{1} \\ c_{2} \\ \\ \\ c_{n} \\ \end{matrix} \right\rbrack \nonumber$$

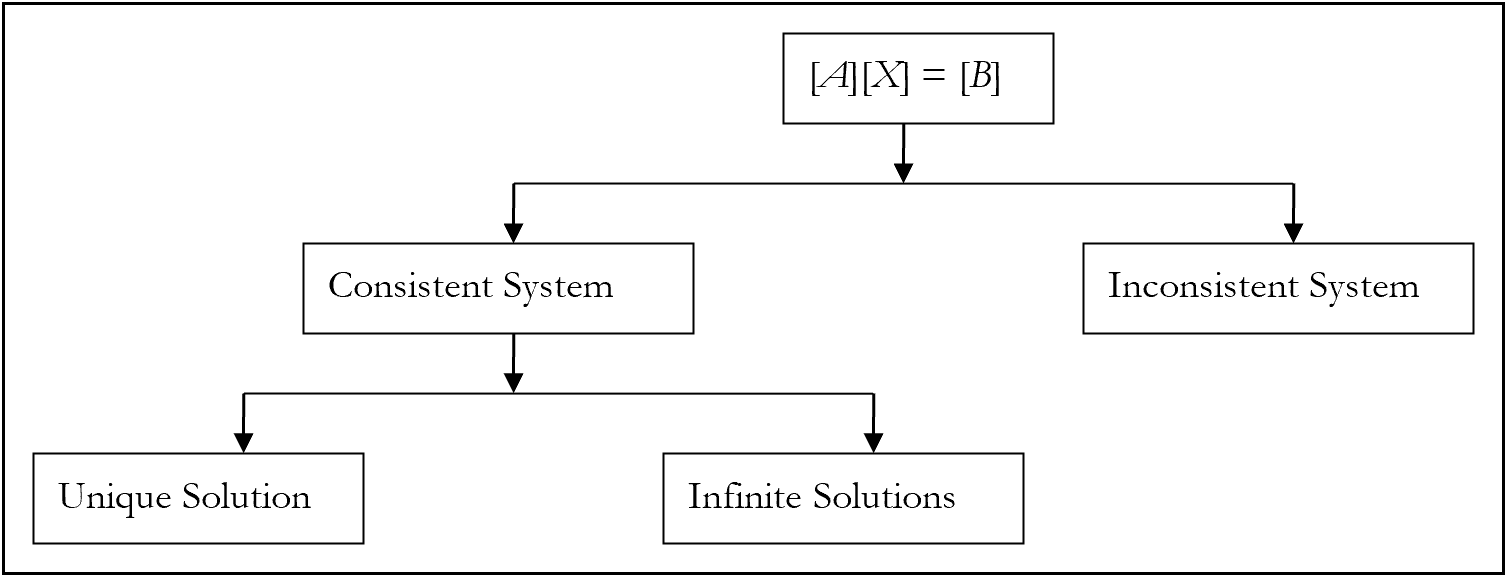
Система рівнянь може бути послідовною або суперечливою. Що це означає?

Система рівнянь$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ є послідовною, якщо є рішення, і вона непослідовна, якщо немає рішення. Однак послідовна система рівнянь не означає унікального рішення, тобто послідовна система рівнянь може мати унікальне рішення або нескінченні розв'язки (рис. 1).

Малюнок$\PageIndex{1}$: Послідовна і непослідовна система рівнянь блок-схема.

Приклад 2

Наведіть приклади послідовної та непослідовної системи рівнянь.

Рішення

1. Система рівнянь

$$\begin{bmatrix} 2 & 4 \\ 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber$$

є послідовною системою рівнянь, оскільки має унікальне рішення, тобто

$$\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} \nonumber$$

2. Система рівнянь

$$\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 3 \\ \end{bmatrix} \nonumber$$

також є послідовною системою рівнянь, але вона має нескінченні розв'язки, наведені нижче.

Розширюючи вищевказаний набір рівнянь,

$$2x + 4y = 6 \nonumber$$

$$x + 2y = 3 \nonumber$$

ви можете бачити, що вони є одним і тим же рівнянням. Отже, будь-яка комбінація$\left( x,y \right)$, що задовольняє

$$2x + 4y = 6 \nonumber$$

це рішення. Наприклад,$\left( x,y \right) = \left( 1,1 \right)$ це рішення. Інші рішення включають$\left( x,y \right) = (0.5,1.25)$$\left( x,y \right) = (0,1.5)$, і так далі.

3. Система рівнянь

$$\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber$$

є непослідовним, оскільки рішення не існує.

Як можна розрізнити послідовну і непослідовну систему рівнянь?

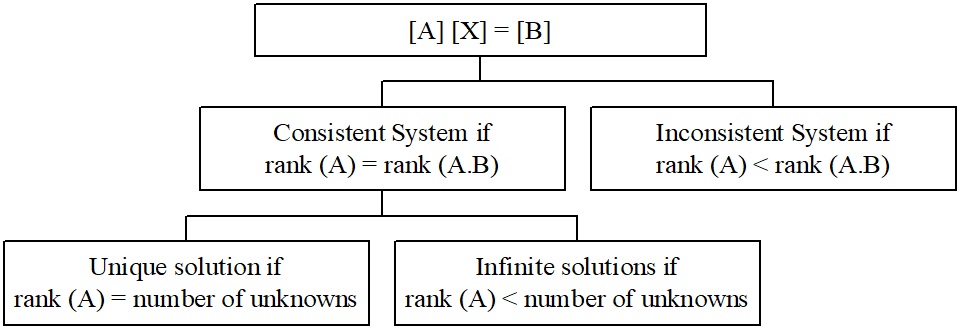
Система рівнянь$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ узгоджена, якщо ранг$A$ дорівнює рангу доповненої матриці.$\left\lbrack A \ \vdots \ C \right\rbrack$

Система рівнянь$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ непослідовна, якщо ранг менше рангу доповненої матриці$\left\lbrack A \ \vdots \ C \right\rbrack$.$A$

Але, що ви маєте на увазі під рангом матриці?

Ранг матриці визначається як порядок найбільшої квадратної підматриці, детермінант якої не дорівнює нулю.

Приклад 3

Що таке ранг

$\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 1 & 2 & 3 \\ \end{bmatrix}$?

Рішення

Найбільша квадратна підматриця можлива порядку 3, і це саме$\lbrack A\rbrack$ по собі. $det(A) = - 23 \neq 0,$З рангу$\lbrack A\rbrack = 3.$

Приклад 4

Що таке ранг

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 5 & 1 & 7 \\ \end{bmatrix}? \nonumber$$

Рішення

Найбільша квадратна$\lbrack A\rbrack$ підматриця має порядок 3, і це саме$\lbrack A\rbrack$ по собі. Так як$det(A) = 0$, ранг менше 3.$\lbrack A\rbrack$ Наступною найбільшою квадратною підматрицею буде$2 \times2$ матриця. Одна з квадратних підматриць$\lbrack A\rbrack$ є

$$\left\lbrack B \right\rbrack = \begin{bmatrix} 3 & 1 \\ 2 & 0 \\ \end{bmatrix} \nonumber$$

і$det(B) = - 2 \neq 0$. Звідси ранг$\lbrack A\rbrack$ дорівнює 2. Немає необхідності дивитися на інші$2 \times 2$ підматриці, щоб встановити, що ранг$\lbrack A\rbrack$ дорівнює 2.

Приклад 5

Як тепер використовувати концепцію рангу, щоб знайти, якщо

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

послідовна або непослідовна система рівнянь?

Рішення

Матриця коефіцієнтів дорівнює

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber$$

і правий бічний вектор

$$\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Розширена матриця

$$\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & \vdots & 106.8 \\ 64 & 8 & 1 & \vdots & 177.2 \\ 144 & 12 & 1 & \vdots & 279.2 \\ \end{bmatrix} \nonumber$$

Оскільки немає квадратних підматриць порядку 4, як$\lbrack B\rbrack$$3 \times 3$ матриця, ранг$\lbrack B\rbrack$ є не більше$3$. Отже, давайте подивимося на квадратні підматриці порядку$3$; якщо будь-яка з цих квадратних підматриць має детермінант не дорівнює нулю, то ранг є$3$.$\lbrack B\rbrack$ Наприклад, підматриця доповненої$\lbrack B\rbrack$ матриці

$$\lbrack D\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber$$

має$det(D) = - 84 \neq 0$.

Звідси ранг доповненої матриці$\lbrack B\rbrack$ дорівнює 3. Так як$\lbrack A\rbrack = \lbrack D\rbrack$, ранг$\lbrack A\rbrack$ дорівнює 3. Оскільки ранг доповненої матриці$\lbrack B\rbrack$ дорівнює рангу матриці коефіцієнтів$\lbrack A\rbrack$, система рівнянь узгоджена.

Приклад 6

Використовуйте поняття рангу матриці, щоб знайти, якщо

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber$$

послідовний або непослідовний?

Рішення

Матриця коефіцієнта задається

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber$$

і з правого боку

$$\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber$$

Розширена матриця

$$\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :284.0 \\ \end{bmatrix} \nonumber$$

Оскільки немає квадратних підматриць порядку 4, як$\lbrack B\rbrack$$4 \times 3$ матриця, ранг доповненої$\lbrack B\rbrack$ становить максимум 3. Отже, давайте подивимося на квадратні підматриці$\lbrack B\rbrack$ доповненої матриці порядку$3$ і подивимося, якщо будь-яка з них має детермінанти не рівні нулю. Наприклад, квадратна підматриця доповненої$\lbrack B\rbrack$ матриці

$$\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber$$

має$det(D) = 0$. Це означає, що нам потрібно дослідити інші квадратні підматриці порядку 3 доповненої матриці$\lbrack B\rbrack$ і знайти їх детермінанти.

Тобто,

$$\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 284.0 \\ \end{bmatrix} \nonumber$$

$$det(E) = 0 \nonumber$$

$$\left\lbrack F \right\rbrack = \begin{bmatrix} 25 & 5 & 106.8 \\ 64 & 8 & 177.2 \\ 89 & 13 & 284.0 \\ \end{bmatrix} \nonumber$$

$$det(F) = 0 \nonumber$$

$$\left\lbrack G \right\rbrack = \begin{bmatrix} 25 & 1 & 106.8 \\ 64 & 1 & 177.2 \\ 89 & 2 & 284.0 \\ \end{bmatrix} \nonumber$$

$$det(G) = 0 \nonumber$$

Всі квадратні підматриці порядку$3 \times 3$ доповненої матриці$\lbrack B\rbrack$ мають нульовий детермінант. Так що ранг доповненої матриці$\lbrack B\rbrack$ менше 3. Чи$\lbrack B\rbrack$ дорівнює ранг доповненої матриці 2?. Однією з$2 \times 2$ підматриць доповненої матриці$\lbrack B\rbrack$ є

$$\left\lbrack H \right\rbrack = \begin{bmatrix} 25 & 5 \\ 64 & 8 \\ \end{bmatrix} \nonumber$$

і

$$det(H) = - 120 \neq 0 \nonumber$$

Отже, ранг доповненої матриці$\lbrack B\rbrack$ дорівнює 2.

Тепер нам потрібно знайти ранг матриці коефіцієнтів$\lbrack B\rbrack$.

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber$$

і

$$det(A) = 0 \nonumber$$

Отже, ранг матриці$\lbrack A\rbrack$ коефіцієнтів менше 3. Квадратна підматриця матриці коефіцієнта$\lbrack A\rbrack$ дорівнює

$$\left\lbrack J \right\rbrack = \begin{bmatrix} 5 & 1 \\ 8 & 1 \\ \end{bmatrix} \nonumber$$

$$det(J) = - 3 \neq 0 \nonumber$$

Отже, ранг матриці коефіцієнтів$\lbrack A\rbrack$ дорівнює 2.

Отже, ранг матриці$\lbrack A\rbrack$ коефіцієнтів дорівнює рангу доповненої матриці$[B]$. Таким чином, система$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ рівнянь послідовна.

Приклад 7

Використовуйте поняття рангу, щоб знайти, якщо

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 280.0 \\ \end{bmatrix} \nonumber$$

є послідовним або непослідовним.

Рішення

Розширена матриця

$$\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :280.0 \\ \end{bmatrix} \nonumber$$

Оскільки немає квадратних підматриць порядку,$4 \times 4$ оскільки доповнена матриця$\lbrack B\rbrack$ є$4 \times 3$ матрицею, ранг доповненої матриці$\lbrack B\rbrack$ становить максимум 3. Отже, давайте подивимося на квадратні підматриці$(B)$ доповненої матриці порядку 3 і подивимося, якщо будь-яка з$3 \times 3$ підматриць має детермінант, не рівний нулю. Наприклад, квадратна підматриця$3 \times 3$ порядку$\lbrack B\rbrack$

$$\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber$$

$$\det(D)\ = \ 0 \nonumber$$

Отже, це означає, що нам потрібно вивчити інші квадратні підматриці доповненої матриці$\lbrack B\rbrack$

$$\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 280.0 \\ \end{bmatrix} \nonumber$$

$det(E) = 12.0 \neq 0$.

Отже, ранг доповненої матриці$\lbrack B\rbrack$ дорівнює 3.

Ранг матриці коефіцієнтів$\lbrack A\rbrack$ - 2 з попереднього прикладу.

Оскільки ранг матриці$\lbrack A\rbrack$ коефіцієнтів менше рангу доповненої матриці$\lbrack B\rbrack$, система рівнянь неузгоджена. Отже, рішення не існує для$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$.

Якщо рішення існує, як ми знаємо, чи є воно унікальним?

У системі рівнянь,$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ яка є послідовною, ранг матриці коефіцієнтів$\lbrack A\rbrack$ такий же, як і доповнена матриця$\lbrack A\left| C \right.\ \rbrack$. Якщо крім того, ранг матриці коефіцієнтів$\lbrack A\rbrack$ збігається з числом невідомих, то рішення унікальне; якщо ранг$\lbrack A\rbrack$ матриці коефіцієнтів менше числа невідомих, то існують нескінченні розв'язки.

Рисунок$\PageIndex{2}$: Блок-схема умов послідовної та непослідовної системи рівнянь.

Приклад 8

Ми виявили, що наступна система рівнянь

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

є послідовною системою рівнянь. Чи має система рівнянь унікальне рішення або вона має нескінченні розв'язки?

Рішення

Матриця коефіцієнтів дорівнює

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber$$

а права сторона

$$\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

З'ясувавши, чи були наведені вище рівняння узгоджені в попередньому прикладі, ми виявили, що ранг матриці коефіцієнтів (A) дорівнює рангу розширеної матриці$\left\lbrack A \ \vdots \ C \right\rbrack$ дорівнює 3.

Рішення є унікальним, оскільки число невідомих = 3 = ранг (A).

Приклад 9

Ми виявили, що наступна система рівнянь

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber$$

є послідовною системою рівнянь. Рішення унікальне або воно має нескінченні рішення.

Рішення

З'ясувавши, чи були наведені вище рівняння послідовними, ми виявили, що ранг матриці$\lbrack A\rbrack$ коефіцієнтів дорівнює рангу доповненої матриці$\left( A \ \vdots\ C \right)$ дорівнює 2.

Оскільки ранг$\lbrack A\rbrack = 2$ < кількість невідомих = 3, існують нескінченні розв'язки.

Якщо у нас більше рівнянь, ніж невідомих у [A] [X] = [C], чи означає це, що система непослідовна?

Ні, це залежить від рангу доповненої матриці$\left\lbrack A\ \vdots \ C \right\rbrack$ і рангу$\lbrack A\rbrack$.

1. Наприклад

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ 284.0 \\ \end{bmatrix} \nonumber$$

послідовний, так як

• ранг доповненої матриці = 3
• ранг матриці коефіцієнта = 3

Тепер, оскільки ранг (A) = 3 = кількість невідомих, рішення є не тільки послідовним, але й унікальним.

2. Наприклад

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ 280.0 \\ \end{bmatrix} \nonumber$$

є непослідовним, так як

• ранг доповненої матриці =$4$
• ранг матриці коефіцієнта =$3$

3. Наприклад

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 50 & 10 & 2 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 213.6 \\ 280.0 \\ \end{bmatrix} \nonumber$$

послідовний, так як

• ранг доповненої матриці = 2
• ранг матриці коефіцієнта = 2

Але оскільки ранг$\lbrack A\rbrack$ = 2 < кількість невідомих = 3, існують нескінченні рішення.

Послідовні системи рівнянь можуть мати тільки унікальне рішення або нескінченні розв'язки. Чи може система рівнянь мати більше одного, але не нескінченну кількість розв'язків?

Ні, ви можете мати тільки унікальне рішення або нескінченні рішення. Припустимо,$\lbrack A\rbrack\lbrack X\rbrack = \lbrack C\rbrack$ є два рішення$\lbrack Y\rbrack$ і$\lbrack Z\rbrack$ так, що

$$\lbrack A\rbrack\lbrack Y\rbrack = \lbrack C\rbrack \nonumber$$

$$\lbrack A\rbrack\lbrack Z\rbrack = \lbrack C\rbrack \nonumber$$

Якщо$r$ константа, то з двох рівнянь

$$r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack = r\left\lbrack C \right\rbrack \nonumber$$

$$\left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber$$

Додавання двох вищевказаних рівнянь дає

$$r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = r\left\lbrack C \right\rbrack + \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber$$

$$\left\lbrack A \right\rbrack\left( r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \right) = \left\lbrack C \right\rbrack \nonumber$$

Звідси

$$r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber$$

це рішення

$$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber$$

Оскільки$r$ є будь-який скалярний, існують нескінченні рішення для$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ форми

$$r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber$$

Чи можете ви розділити дві матриці?

Якщо$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack C\rbrack$ визначено, це може здатися інтуїтивно зрозумілим$\lbrack A\rbrack = \frac{\left\lbrack C \right\rbrack}{\left\lbrack B \right\rbrack}$, але поділ матриці не визначено так. Однак зворотна матриця може бути визначена для певних типів квадратних матриць. Зворотна квадратна матриця$\lbrack A\rbrack$, якщо вона існує, позначається$\lbrack A\rbrack^{- 1}$ таким, що

$$\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack = \lbrack A\rbrack^{- 1}\lbrack A\rbrack \nonumber$$

Де$\lbrack I\rbrack$ знаходиться матриця ідентичності.

Іншими словами, нехай$[A]$ буде квадратна матриця. Якщо$\lbrack B\rbrack$ є ще одна квадратна матриця такого ж розміру$\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, що, то$\lbrack B\rbrack$ є зворотною$\lbrack A\rbrack$. $\lbrack A\rbrack$потім називається бути оборотним або несингулярним. Якщо$\lbrack A\rbrack^{- 1}$ не існує,$\lbrack A\rbrack$ називається незворотним або одниною.

Якщо$\lbrack A\rbrack$ і$\lbrack B\rbrack$ дві$n \times n$ матриці такі що$\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, то ці твердження також вірні.

$[B]$є оберненою$[A]$

$[A]$є оберненою$[B]$

$[A]$і$[B]$ обоє обертаються

$[A]$$[B]$=$[I]$.

$[A]$і$[B]$ обидва неоднини

всі стовпці$[A]$ і$[B]$ лінійно незалежні

всі ряди$[A]$ і$[B]$ лінійно незалежні.

приклад 10

Визначте, чи

$$\lbrack B\rbrack = \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\ \nonumber$$

є оберненою

$$\lbrack A\rbrack = \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix} \nonumber$$

Рішення

$$\begin{split} \lbrack B\rbrack\lbrack A\rbrack &= \ \ \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber$$

Так як

$$\ \left\lbrack B \right\rbrack\left\lbrack A \right\rbrack = \left\lbrack I \right\rbrack, \nonumber$$

$\lbrack B\rbrack$є зворотним$[A]$ і$\lbrack A\rbrack$ є зворотним$\lbrack B\rbrack$.

Але ми також можемо показати, що

$$\begin{split} \lbrack A\rbrack\lbrack B\rbrack &= \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber$$

показати, що$\lbrack A\rbrack$ є зворотним$\lbrack B\rbrack$.

Чи можу я використовувати концепцію зворотної матриці для пошуку розв'язку множини рівнянь [A] [X] = [C]?

Так, якщо кількість рівнянь збігається з кількістю невідомих, матриця коефіцієнтів$\lbrack A\rbrack$ є квадратною матрицею.

Враховується

$$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack \nonumber$$

Потім, якщо$\lbrack A\rbrack^{- 1}$ існує, множимо обидві сторони на$\lbrack A\rbrack^{- 1}$.

$$\lbrack A\rbrack^{- 1}\lbrack A\rbrack\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber$$

$$\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber$$

$$\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber$$

Це означає, що якщо ми можемо знайти$\lbrack A\rbrack^{- 1}$, вектор рішення$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ просто множення$\lbrack A\rbrack^{- 1}$ і правий бік вектора,$\lbrack C\rbrack$.

Як знайти зворотну матрицю?

Якщо$\lbrack A\rbrack$$n \times n$ матриця, то$\lbrack A\rbrack^{- 1}$ є$n \times n$ матрицею і відповідно до визначення зворотної матриці

$$\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack \nonumber$$

Позначаючи

$$\lbrack A\rbrack = \begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix} \nonumber$$

$$\lbrack A\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & \cdot & \cdot & a_{1n}^{'} \\ a_{21}^{'} & a_{22}^{'} & \cdot & \cdot & a_{2n}^{'} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1}^{'} & a_{n2}^{'} & \cdot & \cdot & a_{nn}^{'} \\ \end{bmatrix} \nonumber$$

$$\lbrack I\rbrack = \begin{bmatrix} 1 & 0 & \cdot & \cdot & \cdot & 0 \\ 0 & 1 & & & & 0 \\ 0 & & \cdot & & & \cdot \\ \cdot & & & 1 & & \cdot \\ \cdot & & & & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot & \cdot & 1 \\ \end{bmatrix} \nonumber$$

Використовуючи визначення множення матриці, перший стовпець$\lbrack A\rbrack^{- 1}$ матриці потім можна знайти шляхом вирішення

$$\begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ \cdot \\ \cdot \\ a_{n1}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ \cdot \\ \cdot \\ 0 \\ \end{bmatrix} \nonumber$$

Аналогічно можна знайти і інші стовпці$\lbrack A\rbrack^{- 1}$ матриці, змінивши відповідним чином праву частину.

Приклад 11

Швидкість вгору ракети задається

Таблиця 5.2. Дані про швидкість проти часу для ракети

Час,$t$ (с)	Швидкість руху,$v$ (м/с)
\ (t\) (s) ">5	\ (v\) (м/с) ">106.8
\ (t\) (s) ">8	\ (v\) (м/с) ">177.2
\ (t\) (s) ">12	\ (v\) (м/с) ">279.2

У попередньому прикладі ми хотіли наблизити профіль швидкості за

$$v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber$$

Ми виявили, що коефіцієнти$a,\ b,\ and\ c$ в$v\left( t \right)$ задаються

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Спочатку знайдіть зворотне

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber$$

а потім скористайтеся визначенням зворотного, щоб знайти коефіцієнти$a,\ b,\ and\ c.$

Рішення

Якщо

$$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} \nonumber$$

є зворотним$\lbrack A\rbrack$, то

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \nonumber$$

дає три множини рівнянь

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \nonumber$$

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} \nonumber$$

$$\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \nonumber$$

Розв'язування вищевказаних трьох наборів рівнянь окремо дає

$$\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.04762 \\ - 0.9524 \\ 4.571 \\ \end{bmatrix} \nonumber$$

$$\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} - 0.08333 \\ 1.417 \\ - 5.000 \\ \end{bmatrix} \nonumber$$

$$\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.03571 \\ - 0.4643 \\ 1.429 \\ \end{bmatrix} \nonumber$$

Звідси

$$\lbrack A\rbrack^{- 1} = \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \nonumber$$

Зараз

$$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber$$

де

$$\left\lbrack X \right\rbrack = \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} \nonumber$$

$$\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Використання визначення$\left\lbrack A \right\rbrack^{- 1},$

$$\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber$$

$$\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber$$

$$\begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix}\begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber$$

Звідси

$$\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 0.2905 \\ 19.69 \\ 1.086 \\ \end{bmatrix} \nonumber$$

Так

$$v\left( t \right) = 0.2905t^{2} + 19.69t + 1.086,5 \leq t \leq 12 \nonumber$$

Чи є інший спосіб знайти зворотну матрицю?

Для знаходження оберненої малих матриць зворотну матрицю можна знайти за

$$\left\lbrack A \right\rbrack^{- 1} = \frac{1}{\det\left( A \right)}{adj}\left( A \right) \nonumber$$

де

$${adj}\left( A \right) = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & & C_{2n} \\ \vdots & & & \\ C_{n1} & C_{n2} & \cdots & C_{nn} \\ \end{bmatrix}^{T} \nonumber$$

де$C_{ij}$ знаходяться кофактори$a_{ij}$. Матриця

$$\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & \cdots & C_{2n} \\ \vdots & & & \vdots \\ C_{n1} & \cdots & \cdots & C_{nn} \\ \end{bmatrix} \nonumber$$

сама називається матрицею кофакторів від$[A]$. Кофактори визначені в главі 4.

Приклад 12

Знайти зворотне

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber$$

Рішення

З прикладу 4.6 у розділі 04.06 ми знайшли

$$\det\left( A \right) = - 84 \nonumber$$

Далі нам потрібно знайти суміжні з$\lbrack A\rbrack$. Кофактори$A$ знаходяться наступним чином.

Неповнолітнім в'їздом$a_{11}$ є

$$\begin{split} M_{11} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 8 & 1 \\ 12 & 1 \\ \end{matrix} \right|\\ &= - 4 \end{split} \nonumber$$

Кофакторами вступу$a_{11}$ є

$$\begin{split} C_{11} &= \left( - 1 \right)^{1 + 1}M_{11}\\ &= M_{11}\\ &= - 4 \end{split} \nonumber$$

Неповнолітнім в'їздом$a_{12}$ є

$$\begin{split} M_{12} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 64 & 1 \\ 144 & 1 \\ \end{matrix} \right|\\ &= - 80 \end{split} \nonumber$$

Кофактором входу$a_{12}$ є

$$\begin{split} C_{12} &= \left( - 1 \right)^{1 + 2}M_{12}\\ &= - M_{12}\\ &= - ( - 80)\\ &= 80 \end{split} \nonumber$$

Аналогічно

$$C_{13} = - 384 \nonumber$$

$$C_{21} = 7 \nonumber$$

$$C_{22} = - 119 \nonumber$$

$$C_{23} = 420 \nonumber$$

$$C_{31} = - 3 \nonumber$$

$$C_{32} = 39 \nonumber$$

$$C_{33} = - 120 \nonumber$$

Звідси матриця кофакторів$\lbrack A\rbrack$ є

$$\left\lbrack C \right\rbrack = \begin{bmatrix} - 4 & 80 & - 384 \\ 7 & - 119 & 420 \\ - 3 & 39 & - 120 \\ \end{bmatrix} \nonumber$$

Суміжна матриця$\lbrack A\rbrack$ - це$\lbrack C\rbrack^{T}$,

$$\begin{split} {adj}\left( A \right) &= \left\lbrack C \right\rbrack^{T}\\ &= \begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix} \end{split} \nonumber$$

Звідси

$$\begin{split} \left\lbrack A \right\rbrack^{- 1} &= \frac{1}{\det\left( A \right)}{adj}\left( A \right)\\ &= \frac{1}{- 84}\begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix}\\ &= \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \end{split} \nonumber$$

Якщо зворотна квадратна матриця [A] існує, чи є вона унікальною?

Так, зворотна квадратна матриця є унікальною, якщо вона існує. Доказ полягає в наступному. Припустимо, що зворотне$\lbrack A\rbrack$ є$\lbrack B\rbrack$ і якщо цей зворотний не є унікальним, то нехай інший зворотний$\lbrack A\rbrack$ існувати називається$\lbrack C\rbrack$.

Якщо$\lbrack B\rbrack$ є зворотним$\lbrack A\rbrack$, то

$$\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack \nonumber$$

Помножте обидві сторони на$\lbrack C\rbrack$,

$$\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \lbrack C\rbrack \nonumber$$

$$\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack C\rbrack \nonumber$$

Так$[C]$ як обернена$\lbrack A\rbrack$,

$$\lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \nonumber$$

Помножте обидві сторони на$\lbrack B\rbrack$,

$$\lbrack B\rbrack\ \lbrack I\rbrack\ = \lbrack C\rbrack \nonumber$$

$$\lbrack B\rbrack\ = \lbrack C\rbrack \nonumber$$

Це показує, що$\lbrack B\rbrack$ і$\lbrack C\rbrack$ однакові. Таким чином,$\lbrack A\rbrack$ зворотне є унікальним.

Система рівнянь Вікторина

Вікторина 1

$3 \times 4$Матриця може мати ранг не більше

(А)$3$

(Б)$4$

(С)$5$

(D)$12$

Вікторина 2

Троє дітей — Джим, Корі і Девід отримують спадщину$\text{\$} 2,253,453$. Гроші покладені в три трасти, але не діляться порівну для початку. Корі отримує втричі більше, ніж Девід отримує, тому що Корі зробив «А» в класі доктора Коу. Кожна довіра вкладається в відсоток, що генерує інвестиції. Три трасти Джима, Корі і Девіда платять відсотки$6\%$$8\%$$11\%$, відповідно. Загальний інтерес всіх трьох трастів, об'єднаних в кінці першого року, становить$\text{\$}190,740.57$. Скільки грошей було вкладено в кожен траст? Рівняння в матричній формі

(А)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(Б)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(С)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 6 & 8 & 11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(D)$\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

Вікторина 3

Яка з наведених матриць не має зворотного?

(А)$\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$

(Б)$\begin{bmatrix} 6 & 7 \\ 12 & 14 \\ \end{bmatrix}$

(С)$\begin{bmatrix} 6 & 0 \\ 0 & 7 \\ \end{bmatrix}$

(D)$\begin{bmatrix} 0 & 6 \\ 7 & 0 \\ \end{bmatrix}$

Вікторина 4

множина рівнянь

$$\begin{bmatrix} 1 & 2 & 5 \\ 2 & 3 & 7 \\ 5 & 8 & 19 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 18 \\ 26 \\ 70 \\ \end{bmatrix} \nonumber$$

має

(A) немає рішення

(B) скінченна кількість розв'язків

(C) унікальне рішення

(D) нескінченні рішення

Вікторина 5

Враховуючи систему$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ де$\left\lbrack A \right\rbrack$ -$n \times n$ матриця та$\left\lbrack X \right\rbrack$ та$\left\lbrack C \right\rbrack$$n \times 1$ матриці,$\left\lbrack X \right\rbrack$ існує унікальне рішення, якщо

(А) ранг$\left\lbrack A \right\rbrack =$ рангу$\left\lbrack A \vdots C \right\rbrack$

(B) ранг$\left\lbrack A \right\rbrack =$ рангу$\left\lbrack A \vdots C \right\rbrack = n$

(C) ранг$\left\lbrack A \right\rbrack <$ рангу$\left\lbrack A \vdots C \right\rbrack$

(D) ранг$\left\lbrack A \right\rbrack =$ рангу$\left\lbrack A \vdots C \right\rbrack < n$

Вікторина 6

Якщо$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \begin{bmatrix} - 13 \\ 76 \\ 38 \\ \end{bmatrix}$ і$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 1 & 2 & - 4 \\ - 8 & 2 & 16 \\ 2 & 4 & 8 \\ \end{bmatrix}$ тоді

(А)$\left\lbrack X \right\rbrack = \begin{bmatrix} -13.000 \\ 864.00 \\ 582.00 \\ \end{bmatrix}$

(Б) не можна знайти унікального$\left\lbrack X \right\rbrack$.

(С)$\left\lbrack X \right\rbrack = \begin{bmatrix} -1.0000 \\ 2.0000 \\ 4.0000 \\ \end{bmatrix}$

(D) рішення не$\left\lbrack X \right\rbrack$ можливі

Вправа «Система рівнянь»

Вправа 1

Для набору$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$ рівнянь існує унікальне рішення, якщо

1. ранг (A) = ранг$\left( A\ \vdots\ B \right)$
2. ранг (A) = ранг$\left( A\ \vdots\ B \right)$ і ранг (A) = кількість невідомих
3. ранг (А) = ранг$\left( A\ \vdots\ B \right)$ і ранг (А) = кількість рядів (А).

Відповідь

Б

Вправа 2

ранг матриці

$A = \begin{bmatrix} 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ \end{bmatrix}$є

1. $1$
2. $2$
3. $3$
4. $4$

Вправа 3

$3 \times 4$Матриця може мати ранг не більше

1. $3$
2. $4$
3. $5$
4. $12$

Вправа 4

Якщо$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ має унікальне рішення, де порядок$\lbrack A\rbrack$ є$3 \times 3$,$\lbrack X\rbrack$ є$3 \times 1$, то ранг$\lbrack A\rbrack$ є

1. $2$
2. $3$
3. $4$
4. $5$

Вправа 5

Показати, чи є наступна система рівнянь послідовною чи суперечливою. Якщо вони узгоджені, визначте, чи буде рішення унікальним або нескінченним існувати.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

Відповідь

Послідовний; Нескінченні рішення

Вправа 6

Показати, чи є наступна система рівнянь послідовною чи суперечливою. Якщо вони узгоджені, визначте, чи буде рішення унікальним або нескінченним існувати.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Відповідь

Непослідовний

Вправа 7

Показати, чи є наступна система рівнянь послідовною чи суперечливою. Якщо вони узгоджені, визначте, чи буде рішення унікальним або нескінченним існувати.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 13 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Відповідь

Послідовний; Унікальний

Вправа 8

множина рівнянь

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

має

1. Унікальне рішення
2. Немає рішення
3. Нескінченні рішення

Відповідь

C

Вправа 9

Для яких значень$a$ волі має наступне рівняння

$x_{1} + x_{2} + x_{3} = 4$

$x_{3} = 2$

$\left( a^{2} - 4 \right)x_{1} + x_{3} = a - 2$

1. Унікальне рішення
2. Немає рішення
3. Нескінченні рішення

Відповідь

Якщо$a \neq + 2 \ \text{or} -2,$ тоді буде унікальне рішення Якщо$a = + 2 \ or - 2,$ тоді рішення не буде.
Можливість нескінченних рішень не існує.

Вправа 10

Знайти, якщо

$$\lbrack A\rbrack = \begin{bmatrix} 5 & - 2.5 \\ - 2 & 3 \\ \end{bmatrix} \nonumber$$

і

$$\lbrack B\rbrack = \begin{bmatrix} 0.3 & 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber$$

обернені один одному.

Відповідь

Так

Вправа 11

Знайти, якщо

$$\lbrack A\rbrack = \begin{bmatrix} 5 & 2.5 \\ 2 & 3 \\ \end{bmatrix} \nonumber$$

і

$$lbrack B\rbrack = \begin{bmatrix} 0.3 & - 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber$$

обернені один одному.

Відповідь

Ні

Вправа 12

Знайдіть

1. матриця кофактора
2. суміжній матриці

з

$$\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix} \nonumber$$

Відповідь

$\begin{bmatrix} - 34 & - 18 & 58 \\ - 19 & 7 & 29 \\ 3 & 5 & - 29 \\ \end{bmatrix}\begin{bmatrix} - 34 & - 19 & 3 \\ - 18 & 7 & 5 \\ 58 & 29 & - 29 \\ \end{bmatrix}$

Вправа 13

Знайти,$\lbrack A\rbrack^{- 1}$ використовуючи будь-який метод для
$\lbrack A\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix}$

Відповідь

$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 2.931 \times 10^{- 1} & 1.638 \times 10^{- 1} & - 2.586 \times 10^{- 2} \\ 1.552 \times 10^{- 1} & - 6.034 \times 10^{- 2} & - 4.310 \times 10^{- 2} \\ - 5.000 \times 10^{- 1} & - 2.500 \times 10^{- 1} & 2.500 \times 10^{- 1} \\ \end{bmatrix}$

Вправа 14

Доведіть, що якщо$\lbrack A\rbrack$ і$\lbrack B\rbrack$ обидва оборотні і квадратні матриці того ж порядку, то

$$(\lbrack A\rbrack\lbrack B\rbrack)^{- 1} = \lbrack B\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber$$

Відповідь

$$\left( \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \right)^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber$$

Нехай $$\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber$$

$$\begin{split} \left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} &= \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\\ &= \left\lbrack A \right\rbrack\left\lbrack I \right\rbrack\\ &= \left\lbrack A \right\rbrack \end{split} \nonumber$$

Знову

$\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack$

$$\begin{split} \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack &= \left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack I \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack B \right\rbrack \end{split} \nonumber$$

Так

$$\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack A \right\rbrack ;\;\;\;\;\;\;\ (1) \nonumber$$

$$\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack B \right\rbrack;\;\;\;\;\;\;\ (2) \nonumber$$

Від (1) і (2)

$$\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber$$

$$\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber$$

$$\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber$$

$$\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack \nonumber$$

$$\left\lbrack B^{- 1} \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack^{- 1}\left\lbrack B \right\rbrack \nonumber$$ $$\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack I \right\rbrack. \nonumber$$

Вправа 15

Що таке зворотна квадратна діагональна матриця? Чи завжди вона існує?

Відповідь

Підказка: Обернена квадратом n$\times$ n діагональна матриця$\left\lbrack A \right\rbrack$$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} \frac{1}{a_{11}} & 0 & \cdots & 0 \\ 0 & \frac{1}{a_{22}} & \cdots & 0 \\ 0 & & & \vdots \\ \vdots & \cdots & \cdots & \frac{1}{a_{nn}} \\ \end{bmatrix}$
Отже, обернена існує, лише якщо$a_{ii} \neq 0$ для всіх$i$.

Вправа 16

$\lbrack A\rbrack$і$\lbrack B\rbrack$ квадратні матриці. Якщо$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack 0\rbrack$ і$\lbrack A\rbrack$ є оборотним, покажіть$\lbrack B\rbrack = 0$.

Відповідь

$$\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack 0 \right\rbrack \nonumber$$ $$\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack 0 \right\rbrack \nonumber$$

Вправа 17

Якщо$\lbrack A\rbrack\ \lbrack B\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack$, де$\lbrack A\rbrack$,$\lbrack B\rbrack$ і$\lbrack C\rbrack$ знаходяться однакового розміру, покажіть, що$\lbrack B\rbrack$ є оборотним.

Відповідь

Підказка:$det({AB}) = det(A)det(B)$

Вправа 18

Доведіть, якщо$\lbrack B\rbrack$ є оборотним,$\lbrack A\rbrack\ \lbrack B\rbrack^{- 1} = \lbrack B\rbrack^{- 1}\lbrack A\rbrack$ якщо і тільки якщо$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack B\rbrack\lbrack A\rbrack$

Відповідь

Підказка: помножте$\left\lbrack B \right\rbrack^{- 1}$ на обидві сторони,$\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack^{- 1}$

Вправа 19

Для
$\left\lbrack A \right\rbrack = \begin{bmatrix} 10 & - 7 & 0 \\ - 3 & 2.099 & 6 \\ 5 & - 1 & 5 \\ \end{bmatrix}$
$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} - 0.1099 & - 0.2333 & 0.2799 \\ - 0.2999 & - 0.3332 & 0.3999 \\ 0.04995 & 0.1666 & 6.664 \times 10^{- 5} \\ \end{bmatrix}$
шоу

$${det }\left( A \right) = \frac{1}{{det}\left( A^{- 1} \right)}. \nonumber$$

Вправа 20

Для яких значень$a$ має лінійна система

$$\begin{matrix} x + y = 2 \\ 6x + 6y = a \\ \end{matrix} \nonumber$$

1. нескінченні рішення
2. унікальне рішення

Відповідь

А.$12$

Б. неможливо

Вправа 21

Троє дітей - Джим, Корі і Девід отримують спадщину$\$2,\$253,\$453$. Гроші покладені в три трасти, але не діляться порівну для початку. Корі отримує втричі більше, ніж Девід, тому що Корі зробив «А» в класі доктора Коу. Кожна довіра вкладається в відсоток, що генерує інвестиції. Три трести Джима, Корі і Девіда платить відсотки$6\%, 8\%, 11\%,$ відповідно. Загальний інтерес всіх трьох трастів, об'єднаних в кінці першого року, становить$\$190,\$740.57$. Скільки грошей було вкладено в кожен траст? Встановіть наступне як рівняння у вигляді матриці. Визначте невідомі. Не вирішуйте для невідомих.

Відповідь

$J + C + D = \$2,\$253,\$453$

$$C = 3D \nonumber$$

$$0.06J+0.08C+0.11D = \$190,740.57 \nonumber$$ У матричній формі

$$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 0.06 & 0.08 & 0.11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2,253,453 \\ 0 \\ 190,740.57 \\ \end{bmatrix} \nonumber$$

Вправа 22

Що таке ранг

$$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

У наведеній вище матриці 2 (Рядок 1) + Рядок 2 = Рядок 3. Значить, ранг менше 3. Рядок 1 і Рядок 2 лінійно незалежні. Значить, ранг матриці дорівнює 2.

Вправа 23

Що таке ранг

$$\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 17 \\ 6 & 10 & 13 & 29 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

Визначник всіх$3 \times 3$ підматриць дорівнює нулю. Значить, ранг менше 3. Детермінант

$$\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber$$

Вправа 24

Що таке ранг

$$\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 18 \\ 6 & 10 & 13 & 30 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

У наведеній вище матриці 2 (Рядок 1) + Рядок 2 = Рядок 3. Отже, ранг менше 3, оскільки ряди 3 лінійно залежать. Детермінант

$$\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber$$

Значить, ранг є$2$.

Вправа 25

Скільки розв'язків має наступна система рівнянь

$$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 17 \\ 29 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

Ранг $ A = 2$\ Ранг$A|C = 2$\ Кількість невідомих =$3.$\ Існують нескінченні розв'язки, оскільки ранг A менший за кількість невідомих.

Вправа 26

Скільки розв'язків має наступна система рівнянь

$$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 18 \\ 30 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

Ранг$A = 2$\ Rank of$A|C = 2$\ Число невідомих =$3.$\ Існують нескінченні розв'язки, оскільки ранг A менше числа невідомих.

Вправа 27

Будь-яким науковим методом знайдіть другий стовпець зворотного

$$\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}. \nonumber$$

Відповідь

$\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}\begin{bmatrix} X & a_{12}^{'} & X \\ X & a_{22}^{'} & X \\ X & a_{32}^{'} & X \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

$$\begin{matrix} a_{12}^{'} + 2a_{22}^{'} = 0 \\ 4a_{12}^{'} + 5a_{22}^{'} = 1 \\ 13a_{32}^{'} = 0 \\ \end{matrix} \nonumber$$

Спрощення,

$$\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.667 \\ - 0.333 \\ 0 \\ \end{bmatrix} \nonumber$$

Вправа 28

Просто випишіть зворотне (не потрібно показувати жодної роботи)

$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 5 \\ \end{bmatrix} \nonumber$$

Відповідь

$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 & 0 \\ 0 & 0 & \frac{1}{4} & 0 \\ 0 & 0 & 0 & \frac{1}{5} \\ \end{bmatrix}$

Вправа 29

Вирішити$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$ для$\lbrack X\rbrack\ $ якщо

$$\lbrack A\rbrack^{- 1} = \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix} \nonumber$$

і

$$\lbrack B\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber$$

Відповідь

$$\begin{split} \lbrack X\rbrack = \lbrack A\rbrack - 1\lbrack B\rbrack\ &= \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix}\begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix}\\ &=\begin{bmatrix} 52.5 \\ 49.06 \\ 50.072 \\ \end{bmatrix} \end{split} \nonumber$$

Вправа 30

$\lbrack A\rbrack\ $Дозволяти бути$3 \times 3$ матрицею. Припустимо

$$\lbrack X\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber$$

є розв'язком однорідної множини рівнянь$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$ (права сторона - нульовий вектор порядку$3 \times 1$). Чи$\lbrack A\rbrack$ має зворотний? Обґрунтуйте свою відповідь.

Відповідь

Враховується

$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
Якщо$\lbrack A\rbrack^{- 1}$ існує, то
$\lbrack A\rbrack^{- 1}\ \lbrack A\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack 0\rbrack$
$\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
$\lbrack X\rbrack = \lbrack 0\rbrack$
Це суперечить заданому значенню$\lbrack X\rbrack$. Значить,$\lbrack A\rbrack^{- 1}$ не існує.

Вправа 31

Чи є множиною векторів

$$\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 1 \\ 2 \\ 5 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 1 \\ 4 \\ 25 \\ \end{bmatrix} \nonumber$$

лінійно незалежний? Обґрунтуйте свою відповідь.

Відповідь

Безліч векторів лінійно незалежні.

Вправа 32

Що таке ранг множини векторів

$$\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 1 \\ 2 \\ 5 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 1 \\ 3 \\ 6 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

Оскільки$3$ вектори лінійно незалежні, як доведено вище, ранг 3 векторів є$3$.

Вправа 33

Що таке ранг

$$\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 2 \\ 2 \\ 4 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 3 \\ 3 \\ 5 \\ \end{bmatrix}? \nonumber$$

Обґрунтуйте свою відповідь.

Відповідь

За допомогою огляду,$\overrightarrow{C} = \overrightarrow{A} + \overrightarrow{B}$. Отже, вектори 3 лінійно залежні, а ранг менше 3. Лінійна комбінація$\overrightarrow{A}\text{and}\ \overrightarrow{B}$, тобто$K_{1}\overrightarrow{A} + K_{2}\overrightarrow{B} = 0$ має тільки одне рішення K ₁ = K ₂ = 0. Тому ранг дорівнює 2.