4.5: Набори індексів

Поняття об'єднання можна розширити на три множини:\[A\cup B\cup C = \{x\in{\cal U} \mid (x\in A) \vee (x\in B) \vee (x\in C) \}. \nonumber\] очевидно, як узагальнити його до об'єднання будь-якої кількості множин. Для опису такого союзу ми використовуємо позначення, що нагадує позначення підсумовування:\[\bigcup_{i=1}^n A_i = A_1 \cup A_2 \cup \cdots \cup A_n. \nonumber\] Визначаємо

\[\bigcup_{i=1}^n A_i = \{x\in{\cal U} \mid (x\in A_1) \vee (x\in A_2) \vee\cdots\vee (x\in A_n)\}. \nonumber\]Це виглядає безладно! Ось краща альтернатива:

\[\bigcup_{i=1}^n A_i =\{x\in{\cal U} \mid x\in A_i \mbox{ for } some \, \, i, \mbox{ where } 1\leq i \leq n\}. \nonumber\]

Аналогічним\(\bigcap_{i=1}^n A_i = A_1 \cap A_2 \cap \cdots \cap A_n\) чином і визначаємо

\ [\ bigcap_ {i = 1} ^n a_i
=\ {x\ in {\ cal U}\ середина х\ в a_i\ mbox {для} все\,\, i,
\ mbox {де} 1\ leq i\ leq n\}\ nonnumber\]

Простою англійською мовою,\(\bigcup_{i=1}^n A_i\) це колекція всіх елементів в\(A_i\) 's, і\(\bigcap_{i=1}^n A_n\) це колекція всіх елементів, загальних для всіх\(A_i\).

Приклад\(\PageIndex{1}\label{eg:indexset-01}\)

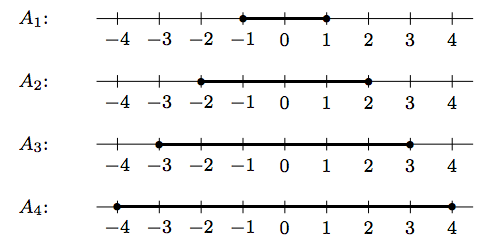
Бо\(i=1,2,3,\ldots\,\), нехай\(A_i = [-i,i]\). По-перше, побудуйте кілька\(A_i\) для порівняння, оскільки це може допомогти нам виявити будь-яку конкретну закономірність. Див. Малюнок\(\PageIndex{1}\) нижче. Зрозуміло, що\(A_1 \subset A_2 \subset \cdots\,\). Таким чином\(\bigcup_{i=1}^n A_i = [-n,n] = A_n\), і\(\bigcap_{i=1}^n A_i = [-1,1] = A_1\).

Малюнок\(\PageIndex{1}\): Порівняння інтервалів, щоб знайти їх об'єднання і перетин.

практичні вправи\(\PageIndex{1}\label{he:indexset-01}\)

Оцініть\(\bigcup_{i=1}^n B_i\) і\(\bigcap_{i=1}^n B_i\), де\(B_i = [0,2i)\).

Очевидно, що ми також можемо продовжити верхню межу до нескінченності. \[\begin{aligned} \bigcup_{i=1}^\infty A_i &=& A_1 \cup A_2 \cup \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for }some \, \, i \in \mathbb{N} \}, \\ \bigcap_{i=1}^\infty A_i &=& A_1 \cap A_2 \cap \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for } all \, \, i \in \mathbb{N} \}. \end{aligned} \nonumber\]У деяких ситуаціях ми можемо запозичити ідею часткових сум з числення. Спочатку знаходимо об'єднання або перетин перших\(n\) множин, потім беремо межу, як\(n\) наближається до нескінченності. Таким чином, якщо межа чітко визначена, то

\[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcup_{i=1}^n A_i, \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcap_{i=1}^n A_i. \nonumber\]

Приклад\(\PageIndex{2}\label{eg:indexset-02}\)

Нехай\(A_i = [-i,i]\). З останнього прикладу ми дізналися, що\(\bigcup_{i=1}^n A_i = [-n,n]\) і\(\bigcap_{i=1}^n A_i = [-1,1]\). Отже,\[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} [-n,n] = (-\infty,\infty), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = [-1,1]. \nonumber\] нагадаємо, що ми пишемо\((-\infty,\infty)\) замість того,\([-\infty,\infty]\) що\(\pm\infty\) не числа, вони є лише символами, що представляють нескінченно великі значення.

практичні вправи\(\PageIndex{2}\label{he:indexset-02}\)

Оцініть\(\bigcup_{i=1}^\infty B_i\) і\(\bigcap_{i=1}^\infty B_i\), де\(B_i = [0,2i)\).

Приклад\(\PageIndex{3}\label{eg:indexset-03}\)

Нехай\(B_i = \left(0,1-\frac{1}{2i}\right]\). Визначити\(\bigcup_{i=1}^\infty B_i\) і\(\bigcap_{i=1}^\infty B_i\).

Рішення

Знову ж таки, у нас є\(B_1 \subset B_2 \subset \cdots\,\). Це легко перевірити Це\[\bigcup_{i=1}^n B_i = B_n = \left(0,1-\frac{1}{2n}\right], \qquad\mbox{and}\qquad \bigcap_{i=1}^n B_i = B_1 = \left(0,\frac{1}{2}\right]. \nonumber\] випливає, що\[\bigcup_{i=1}^\infty B_i = \lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] = (0,1), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty B_i = \left(0,\frac{1}{2}\right]. \nonumber\] Зверніть увагу, що\(\lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] \neq (0,1]\) тому, що кінцева точка 1 не належить жодному\(B_i\).

практичні вправи\(\PageIndex{3}\label{he:indexset-03}\)

Нехай\(C_i = \left[0,1-\frac{1}{i}\right]\). Визначити\(\bigcup_{i=1}^\infty C_i\) і\(\bigcap_{i=1}^\infty C_i\).

Приклад\(\PageIndex{4}\label{eg:indexset-04}\)

Нехай\(D_i = \left(1-\frac{1}{i},1+\frac{1}{i}\right)\). Визначити\(\bigcup_{i=1}^\infty D_i\) і\(\bigcap_{i=1}^\infty D_i\).

Рішення

У міру\(i\) збільшення значення значення\(\frac{1}{i}\) зменшується. Значить, ліва кінцева точка\(1-\frac{1}{i}\) збільшується, а права кінцева точка\(1+\frac{1}{i}\) зменшується.

\[\begin{array}{|c|c|} \hline i & D_i = \big(1-\frac{1}{i},1+\frac{1}{i}\big) \\ \hline 1 & (0,2) \\ 2 & \big(\frac{1}{2},\frac{3}{2}\big) \\ 3 & \big(\frac{2}{3},\frac{4}{3}\big) \\ 4 & \big(\frac{3}{4},\frac{5}{4}\big) \\ \hline \end{array} \nonumber\]

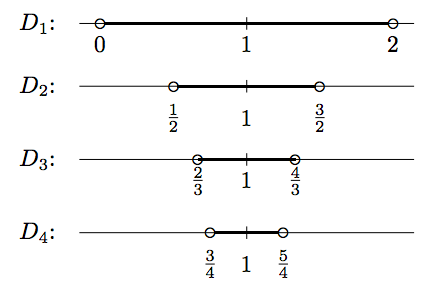
Зрозуміло, що\(D_1\supseteq D_2 \supseteq D_3 \supseteq \cdots\,\). Таким чином\(\bigcup_{i=1}^\infty D_i = D_1 = (0,2)\), і\(\bigcap_{i=1}^\infty D_i = \{1\}\).

практичні вправи\(\PageIndex{4}\label{he:indexset-04}\)

Нехай\(E_i = \left[-i,1+\frac{1}{i}\right)\). Визначити\(\bigcup_{i=1}^\infty E_i\) і\(\bigcap_{i=1}^\infty E_i\).

практичні вправи\(\PageIndex{5}\label{he:indexset-05}\)

Для кожного натурального цілого числа\(i\) визначте\(F_i=\{i,i+1,i+2,\ldots,3i\}\). Визначити\(\bigcup_{i=1}^\infty F_i\) і\(\bigcap_{i=1}^\infty F_i\).

Наступні два результати очевидні.

Теорема\(\PageIndex{1}\label{subsetcap}\)

Якщо\(A_1 \subseteq A_2 \subseteq A_3 \subseteq \cdots\,\), то\(\bigcap_{i=1}^\infty A_i = A_1\).

Теорема\(\PageIndex{2}\)

Якщо\(A_1 \supseteq A_2 \supseteq A_3 \supseteq \cdots\), то\(\bigcup_{i=1}^\infty A_i = A_1\).

Як ми могли б описати союз\(A_2 \cup A_4 \cup A_6 \cup \cdots\,\)? Ну, ми можемо написати,\[\bigcup_{i \small \, even} A_i, \nonumber\] що означає, що союз\(A_i\),\(i\) де навіть. Так як множина парних натуральних чисел позначається символом\(2\mathbb{N}\), інший спосіб опису того ж союзу -\[\bigcup_{i\in2\mathbb{N}} A_i. \nonumber\] це означає об'єднання все\(A_i\), де\(i\) виймається з безлічі\(2\mathbb{N}\). Відповідно,\[\bigcup_{i=0}^\infty A_i = \bigcup_{i\in\mathbb{N}} A_i, \qquad\mbox{and}\qquad \bigcap_{i=0}^\infty A_i = \bigcap_{i\in\mathbb{N}} A_i. \nonumber\] Ми можемо навіть піти на крок далі,\(i\) дозволяючи бути взяті з будь-якого набору цілих чисел, або будь-якого набору дійсних чисел, або навіть будь-якого набору об'єктів. Єдине обмеження - це те, що\(A_i\) повинно існувати, і його зміст повинен якось залежати від\(i\).

Загалом, з огляду на непорожній набір\(I\), якби ми могли асоціювати з кожним\(i\in I\) множиною\(A_i\), ми визначаємо індексоване сімейство множин,\({\cal A}\) як\[{\cal A} = \{ A_i \mid i\in I \}. \nonumber\] Ми називаємо\(I\) набір індексів, і визначити\[\begin{aligned} \bigcup_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for }some \, \, i\in I \}, \\ \bigcap_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for } all \, \, i\in I \}. \end{aligned} \nonumber\] Давайте розглянемо кілька приклади.

Приклад\(\PageIndex{5}\label{eg:indexset-05}\)

Для опису об'єднання\[A_1\cup A_3\cup A_7\cup A_{11}\cup A_{23}, \nonumber\] ми спочатку визначаємо індекс set to be\(I=\{1,3,7,11,23\}\), який є набором усіх індексів, що використовуються в об'єднанні. Тепер союз можна зручно описати як\(\bigcup_{i\in I} A_i\).

Приклад\(\PageIndex{6}\label{eg:indexset-06}\)

Розглянемо п'ять наборів\[\begin{array}{r c l} A_1 &=& \{1,4,23\}, \\ A_2 &=& \{7,11,23\}, \\ A_3 &=& \{3,6,9\}, \\ A_4 &=& \{5,17,22\}, \\ A_5 &=& \{3,6,23\}. \end{array} \nonumber\] Нехай\(I=\{2,5\}\), потім\[\bigcup_{i\in I} A_i = A_2 \cup A_5 = \{7,11,23\} \cup \{3,6,23\} = \{3,6,7,11,23\}. \nonumber\] Аналогічно,\(\bigcap_{i\in I} A_i = A_2 \cap A_5 = \{7,11,23\} \cap \{3,6,23\} = \{23\}\).

практичні вправи\(\PageIndex{6}\label{he:indexset-06}\)

Нехай\(J=\{1,4,5\}\). Оцініть\(\bigcup_{i\in J} A_i\) і\(\bigcap_{i\in J} A_i\), де\(A_i\) s визначені в останньому прикладі.

практичні вправи\(\PageIndex{7}\label{he:indexset-07}\)

Набір індексів може бути набором будь-яких об'єктів. Наприклад, набори чисел в останньому прикладі можуть бути улюбленими номерами Лото п'яти різних студентів. Ми могли б проіндексувати ці набори відповідно до імен учнів:\[\begin{array}{r c l} A_{\small John} &=& \{1,4,23\}, \\ A_{\small Mary} &=& \{7,11,23\}, \\ A_{\small Joe} &=& \{3,6,9\}, \\ A_{\small Pete} &=& \{5,17,22\}, \\ A_{\small Lucy} &=& \{3,6,23\}. \end{array} \nonumber\] Якщо\(I=\{\mbox{Mary},\mbox{Joe},\mbox{Lucy}\}\), що таке\(\bigcup_{i\in I}\)? Як би ви інтерпретували його фізичний сенс?

приклад\(\PageIndex{7}\label{eg:indexset-07}\)

Нехай\(I = \{x\mid x \mbox{ is a living human being} \,\}\), і визначити\[\begin{array}{r c l} B_i &=& \{ x \in I \mid x \mbox{ is a child of } i \}, \\ A_i &=& \{ i \} \cup B_i \end{array} \nonumber\] для кожного\(i\in I\). Тоді\[\bigcap_{i\in I} A_i = \emptyset, \qquad \bigcup_{i\in I} A_i = I, \qquad \bigcap_{i\in I} B_i = \emptyset, \nonumber\] і\[\bigcup_{i\in I} B_i = I - \{ x \mid x\mbox{'s parents are both deceased}\,\}. \nonumber\] Ми залишаємо це як вправу для перевірки цих спілок і перетинів.

практичні вправи\(\PageIndex{8}\label{he:indexset-08}\)

Перевірте перетин і об'єднання в останньому прикладі.

Практічні вправи\(\PageIndex{9}\label{he:indexset-09}\)

Якщо\(I\) являє собою набір учнів, і\(A_i\) являє собою набір друзів учня\(i\), інтерпретувати значення\(\bigcup_{i\in I} A_i\) і\(\bigcap_{i\in I} A_i\).

Закриваємо цей розділ ще одним узагальненням законів Де Моргана.

Теорема\(\PageIndex{3}\) Extended De Morgan's laws

Для будь-якого непорожнього набору\(I\) індексу ми маємо\[\overline{\bigcup_{i\in I} A_i} = \bigcap_{i\in I} \overline{A_i}, \qquad\mbox{ and }\qquad \overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}. \nonumber\]

Доказ 1

Нехай\(x\in \overline{\bigcup_{i\in I} A_i}\), тоді\[x\notin \bigcup_{i\in I} A_i = \{ x \mid x\in A_i \mbox{ for } some \,\, i\in I \}. \nonumber\] це означає\(x\notin A_i\) для кожного\(i\in I\). Значить,\(x\in \overline{A_i}\) для кожного\(i\in I\). Отже,\[x\in \bigcap_{i\in I} \overline{A_i}. \nonumber\] Це доводить це\(\overline{\bigcup_{i\in I} A_i} \subseteq \bigcap_{i\in I} \overline{A_i}\).

Далі нехай\(x\in \bigcap_{i\in I} \overline{A_i}\). Потім\(x\in \overline{A_i}\) для кожного\(i\in I\). Це засіб\(x\notin A_i\) для кожного\(i\in I\). Тоді\[x\notin \{ x \mid x\in A_i \mbox{ for }some \,\, i\in I \} = \bigcup_{i\in I} A_i. \nonumber\] Таким чином\(x\in \overline{\bigcup_{i\in I} A_i}\), доводячи це\(\bigcap_{i\in I} \overline{A_i} \subseteq \overline{\bigcup_{i\in I} A_i}\). Раніше ми це довели\(\overline{\bigcup_{i\in I} A_i} \subseteq \bigcap_{i\in I} \overline{A_i}\). Тому два набори повинні бути рівними.
Доказ\(\overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\) виручки аналогічним чином і залишається як вправа.

Доказ 2

Доведемо\(\overline{\bigcup_{i\in I} A_i} = \bigcap_{i\in I} \overline{A_i}\). Ми залишаємо пояснення для заповнення:\[\begin{array}{r c l} x\in \overline{\bigcup_{i\in I} A_i} &\Leftrightarrow& \overline{x\in \bigcup_{i\in I} A_i} \\ &\Leftrightarrow& \overline{x\in A_i \mbox{ for some $i$}} \\ &\Leftrightarrow& x\notin A_i \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \overline{A_i} \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \bigcap_{i\in I} \overline{A_i}. \end{array} \nonumber\] Доказ\(\overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\) залишається як вправа.

Резюме та огляд

• Маючи справу з довільним перетином або об'єднанням інтервалів, спочатку визначте кінцеві точки, а потім проаналізуйте набори, що беруть участь в операції, щоб визначити, чи слід включати кінцеву точку або виключати.
• Перетин і об'єднання можуть виконуватися на групі подібних множин, ідентифікованих індексами, що належать до набору індексів.
• Отже, перетин або об'єднання можуть бути сформовані шляхом іменування певного набору індексів.

Вправи 4.5

Вправа\(\PageIndex{1}\label{ex:indexset-01}\)

Для кожного\(n\in\mathbb{Z}^+\) визначте\(A_n=\left(-\frac{1}{n},2n\right)\). Знайти\(\bigcap_{n=1}^\infty A_n\) і\(\bigcup_{n=1}^\infty A_n\).

Вправа\(\PageIndex{2}\label{ex:indexset-02}\)

Для кожного\(n\in\mathbb{Z}^+\) визначте\(B_n = \{m\in\mathbb{Z} \mid -\frac{n}{2}\leq m\leq 3n\}\). Оцініть\(\bigcap_{n=1}^\infty B_n\) і\(\bigcup_{n=1}^\infty B_n\).

Вправа\(\PageIndex{3}\label{ex:indexset-03}\)

Визначте\(C_n=\{n,n+1,n+2,\ldots,2n+1\}\) для кожного цілого числа\(n\geq0\). Оцініть\(\bigcap_{n=0}^\infty C_n\) і\(\bigcup_{n=0}^\infty C_n\).

Вправа\(\PageIndex{4}\label{ex:indexset-04}\)

Для кожного\(n\in I = \{1,2,3,\ldots,100\}\) визначте\(D_n=[-n,2n]\cap\mathbb{Z}\). Оцініть\(\bigcap_{n\in I} D_n\) і\(\bigcup_{n\in I} D_n\).

Вправа\(\PageIndex{5}\label{ex:indexset-05}\)

Для кожного\(n\in\mathbb{N}\) визначте\(E_n = \{-n,-n+1,-n+2,\ldots,n^2\}\). Оцініть\(\bigcap_{n\in\mathbb{N}} E_n\) і\(\bigcup_{n\in\mathbb{N}} E_n\).

Вправа\(\PageIndex{6}\label{ex:indexset-06}\)

Для кожного\(n\in\mathbb{N}\) визначте\(F_n = \left\{\frac{m}{n} \mid m\in\mathbb{Z}\right\}\). Оцініть\(\bigcap_{n\in\mathbb{N}} F_n\) і\(\bigcup_{n\in\mathbb{N}} F_n\).

Вправа\(\PageIndex{7}\label{ex:indexset-07}\)

Нехай\(I=(0,1)\), і визначити\(A_i = \left[1,\frac{1}{i}\right]\) для кожного\(i\in I\). Наприклад\(A_{0.5} = [1,2]\) і\(A_{\frac{\pi}{4}} = \left[1,\frac{4}{\pi}\right]\). Оцініть\(\bigcup_{i\in I} A_i\) і\(\bigcap_{i\in I} A_i\).

Вправа\(\PageIndex{8}\label{ex:indexset-08}\)

Визначте\(I=(0,1)\), і для кожного\(i\in I\), нехай\(B_i=(-i,\frac{1}{i})\). Оцініть\(\bigcup_{i\in I} B_i = (-1,\infty)\) і\(\bigcap_{i\in I} B_i\).

Вправа\(\PageIndex{9}\label{ex:indexset-09}\)

Оцініть\(\bigcap_{x\in(1,2)} (1-2x,x^2)\) і\(\bigcup_{x\in(1,2)} (1-2x,x^2)\).

Вправа\(\PageIndex{10}\label{ex:indexset-10}\)

Оцініть\(\bigcap_{x\in(0,1)} \left(x,\frac{1}{x}\right)\) і\(\bigcup_{x\in(0,1)} \left(x,\frac{1}{x}\right)\).

Вправа\(\PageIndex{11}\label{ex:indexset-11}\)

Нехай універсальний набір буде\(\mathbb{R}^2\). Для кожного визначте\(r\in(0,\infty)\),\[A_r = \{(x,y)\mid y=rx^2\}; \nonumber\] тобто,\(A_r\) це множина точок на параболі\(y=rx^2\), де\(r>0\). Оцініть\(\bigcap_{r\in(0,\infty)} A_r\) і\(\bigcup_{r\in(0,\infty)} A_r\).

Вправа\(\PageIndex{12}\label{ex:indexset-12}\)

Доведіть, що\( \overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\) для будь-якого непорожнього набору індексу\(I\).