1.E: Основи (вправи)

1.2: Приклади

Вправа\(\PageIndex{2.1}\)

Поясніть, чому\(m\times n\) дошка може бути покрита,\(n\) якщо\(m\) або навіть. Поясніть, чому це не може бути охоплено, якщо обидва\(m\) і\(n\) непарні.

Вправа\(\PageIndex{2.2}\)

Припустимо, два діагонально протилежних кута звичайної\(8\times8\) дошки видалені. Чи можна покрити отриману дошку?

Вправа\(\PageIndex{2.3}\)

Припустимо, що\(m\) і\(n\) обидва непарні. На\(m\times n\) дошці, пофарбованої як зазвичай, всі чотири кути будуть одного кольору, скажімо білого. Припустимо, з дошки видалений один білий квадрат. Покажіть, що вийшла дошку можна накрити.

Вправа\(\PageIndex{2.4}\)

Припустимо, що один кут\(8\times 8\) дошки видалений. Чи можна залишок покрити\(1\times 3\) плиткою? Покажіть плитку або доведіть, що це неможливо зробити.

Вправа\(\PageIndex{2.5}\)

Припустимо, квадрат в рядку 3, стовпець 3\(8\times8\) дошки видаляється. Чи можна залишок покрити\(1\times 3\) плиткою? Покажіть плитку або доведіть, що це неможливо зробити.

Вправа\(\PageIndex{2.6}\)

Видаліть два діагонально протилежні кути\(m\times n\) дошки, де\(m\) непарний і\(n\) парний. Покажіть, що залишок можна покрити доміно.

Вправа\(\PageIndex{2.7}\)

Припустимо, один білий і один чорний квадрат видалені з\(n\times n\) дошки,\(n\) навіть. Покажіть, що залишок може бути покритий доміно.

Вправа\(\PageIndex{2.8}\)

Припустимо,\(n\times n\) дошка,\(n\) рівна, покрита доміно. Показати, що кількість горизонтальних доміно з білим квадратом під лівим кінцем дорівнює кількості горизонтальних доміно з чорним квадратом під лівим кінцем.

Вправа\(\PageIndex{2.9}\)

У повному графіку на п'яти вершині, показаних вище, є п'ять пар ребер, які перетинаються. Намалюйте цей графік так, щоб тільки одна пара ребер перетиналася. Пам'ятайте, що «краю» не обов'язково повинні бути прямими.

Вправа\(\PageIndex{2.10}\)

Повний двороздільний граф\(K_{3,3}\) складається з двох груп по три вершини кожна, з усіма можливими ребрами між групами і без інших ребер:

Малюнок\(\PageIndex{1}\)

Намалюйте цей графік лише одним перетином.

1.3: Комбінації та перестановки

Вправа\(\PageIndex{3.1}\)

Скільки позитивних факторів\(2\cdot3^4\cdot7^3\cdot11^2\cdot47^5 \) має? Скільки\(p_1^{e_1}p_2^{e_2}\cdots p_n^{e_n} \) має, де\(p_i \) є різні прості числа?

Вправа\(\PageIndex{3.2}\)

Рука покеру складається з п'яти карт зі стандартної колоди 52 карт з чотирма мастями і тринадцятьма значеннями в кожній масті; порядок карт в руці не має значення. Скільки рук складаються з 2-х карт з одним значенням і 3 карт іншого значення (фулл-хаус)? Скільки складається з 5 карт з однієї масті (флеш)?

Вправа\(\PageIndex{3.3}\)

Шість чоловіків і шість жінок повинні сидіти за столом, а чоловіки та жінки чергуються. Стільці не мають значення, тільки хто поруч з ким, але правий і лівий різні. Скільки можливих місць для розсадження?

Вправа\(\PageIndex{3.4}\)

Вісім людей повинні сидіти за столом; стільці не мають значення, тільки хто поруч з ким, а справа і ліворуч різні. Двоє людей, X і Y, не можуть сидіти поруч один з одним. Скільки можливих місць для розсадження?

Вправа\(\PageIndex{3.5}\)

У шахах тура атакує будь-яку фігуру в тому ж рядку або стовпці, що і тура, за умови, що між ними немає іншої фігури. Скільки способів можна розмістити вісім граків на шаховій дошці, щоб жоден з двох не нападав один на одного? А як щодо восьми граків на\(10\times 10 \) дошці?

Вправа\(\PageIndex{3.6}\)

Припустимо, що ми хочемо розмістити 8 неатакуючих тури на шахівниці. Скільки способів ми можемо це зробити, якщо 16 найбільш «північно-західних» квадратів повинні бути порожніми? Як щодо того, якщо тільки 4 найбільш «північно-західні» площі повинні бути порожніми?

Вправа\(\PageIndex{3.7}\)

«Юридична» послідовність дужок - це та, в якій дужки можуть бути правильно підібрані, як\(()(())\). Неважко помітити, що це можливо саме тоді, коли кількість лівої та правої дужок однакова, а кожен початковий сегмент послідовності має принаймні стільки ж лівих дужок, скільки правої. Наприклад,\(())\ldots \) неможливо розширити до правової послідовності. Показати, що кількість правових послідовностей довжини\(2n \) дорівнює\(C_n={2n\choose n}-{2n\choose n+1}\). Цифри\(C_n \) називаються каталонськими цифрами.

1.4: Біноміальні коефіцієнти

Вправа\(\PageIndex{4.1}\)

Припустимо, що вулична сітка починається з позиції\((0,0)\) і простягається вгору і вправо:

Малюнок\(\PageIndex{1}\)

Найкоротший маршрут по вулицях від\((0,0)\) до\((i,j)\) - це\(i+j\) блоки довжиною, що йде\(i\) кварталами на схід і\(j\) кварталами на північ. Скільки існує таких маршрутів? Припустимо, що блок між\((k,l)\) і\((k+1,l)\) закритий, де\(k< i\) і\(l\le j\). Скільки найкоротших маршрутів від\((0,0)\) до\((i,j)\)?

Вправа \(\PageIndex{4.2}\)

Доведіть шляхом індукції, що\(\sum_{k=0}^n {k\choose i} = {n+1\choose i+1}\) для\(n\ge 0\) і\(i\ge 0\).

Вправа\(\PageIndex{4.3}\)

Використовуйте комбінаторний аргумент, щоб довести, що\(\sum_{k=0}^n {k\choose i} = {n+1\choose i+1}\) для\(n\ge 0\) і\(i\ge 0\); тобто пояснити, чому ліва сторона вважає те ж саме, що і права сторона.

Вправа\(\PageIndex{4.4}\)

Використовуйте комбінаторний аргумент, щоб довести це\({k \choose 2} + {n-k \choose 2}+k(n-k) = {n \choose 2}\).

Вправа\(\PageIndex{4.5}\)

Використовуйте комбінаторний аргумент, щоб довести,\({2n\choose n}\) що парний.

Вправа\(\PageIndex{4.6}\)

Припустимо, що\(A\) це непорожня скінченна множина. Доведіть, що\(A\) має стільки парних підмножин, як це робить непарного розміру підмножин.

Вправа\(\PageIndex{4.7}\)

Доведіть, що\(\sum_{k=0}^n {k\choose i}k = {n+1\choose i+1}n-{n+1\choose i+2}\) для\(n\ge 0\) і\(i\ge 0\).

Вправа\(\PageIndex{4.8}\)

Переконайтеся, що\({n+1\choose2}+{n\choose2}=n^2\). Використовуйте Вправу\(\PageIndex{4.2}\), щоб знайти простий вираз для\(\sum_{i=1}^n i^2\).

Вправа\(\PageIndex{4.9}\)

Зробіть здогаду про суми висхідних діагоналей у трикутнику Паскаля, як зазначено. Доведіть, що ваша здогадка вірна.

Малюнок\(\PageIndex{2}\)

Вправа\(\PageIndex{4.10}\)

Знайти кількість способів запису\(n\) як впорядковану суму одиниць і двійки,\(n\ge 0\). Наприклад, коли\(n=4\), існує п'ять способів:\(1+1+1+1\),\(2+1+1\),\(1+2+1\),\(1+1+2\), і\(2+2\).

Вправа\(\PageIndex{4.11}\)

Використовуйте\((x+1)^n=\sum_{i=0}^n{n\choose i}x^i\) для пошуку простого виразу для\(\sum_{i=0}^n{1\over i+1}{n\choose i}x^{i+1}\). Тоді знайдіть простий вираз для\(\sum_{i=0}^n{1\over i+1}{n\choose i}\).

Вправа\(\PageIndex{4.12}\)

Використовуйте попередню вправу, щоб знайти простий вираз для\(\sum_{i=0}^n(-1)^i{1\over i+1}{n\choose i}\).

Вправа\(\PageIndex{4.13}\)

Дайте комбінаторний доказ\[\sum_{i=0}^k {m\choose i}{n\choose k-i}={m+n\choose k}.\nonumber\] перепишіть цю ідентичність в простішій формі\(m=n\), якщо і коли\(k=m=n\).

Вправа\(\PageIndex{4.14}\)

Завершіть доказ теореми 1.4.3.

Вправа\(\PageIndex{4.15}\)

Дайте альтернативний доказ теореми 1.4.3, охарактеризувавши ті,\(i\) для яких\({n\choose i}/{n\choose i-1} > 1\).

Вправа\(\PageIndex{4.16}\)

Коли\({n\choose i}/{n\choose i-1}\) максимум? Коли це\({n\choose i}/{n\choose i-1}=2\)?

Вправа\(\PageIndex{4.17}\)

Коли\({n\choose i}-{n\choose i-1}\) максимум?

Вправа\(\PageIndex{4.18}\)

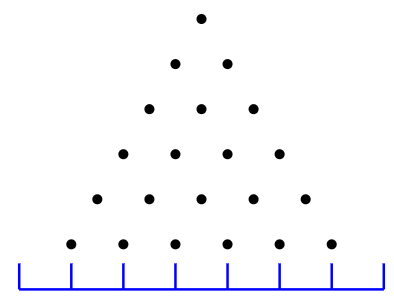
Дошка Галтона - це вертикальна плоска поверхня з виступаючими горизонтальними штирями, розташованими, як показано нижче. Внизу - кількість бункерів; якщо кількість рядів дорівнює\(n\), то кількість бункерів дорівнює\(n+1\). Куля опускається прямо над верхнім штирем, і на кожному штирі відскакує вліво або вправо з однаковою ймовірністю. Ми припускаємо, що наступний м'яч потрапляє в штифт внизу і відразу ліворуч або праворуч від удару шпильки, і це триває вниз по дошці, поки м'яч не впаде в відро внизу. Якщо ми пронумеруємо бункери від 0 до\(n\), скільки шляхів може рухатися м'яч, щоб в кінцевому підсумку в смітник\(k\)?

Це може бути інтерпретовано з точки зору ймовірності, яка була наміром сера Френсіса Галтона, коли він його проектував. Кожен шлях однаково імовірно буде прийнятий м'ячем. Якщо випало багато куль, кількість куль у смітнику\(k\) відповідає ймовірності опинитися в цьому смітнику. Чим більше шляхів закінчується в смітнику, тим вище ймовірність. Коли випадає дуже велика кількість куль, кулі утворюватимуть наближення до кривої дзвінка, знайомої з ймовірності та статистики.

Є анімація процесу за адресою http://www.math.uah.edu/stat/apps/GaltonBoardExperiment.html. Була колись дуже приємна фізична реалізація в Тихоокеанському науковому центрі в Сіетлі.

Малюнок\(\PageIndex{3}\)

1.5: Числа дзвонів

Вправа\(\PageIndex{5.1}\)

Показати, що якщо\(\{A_1,A_2,\ldots,A_k\}\) є розділом\(\{1,2,\ldots,n\}\), то існує унікальне відношення еквівалентності, класи еквівалентності\(\equiv\) яких є\(\{A_1,A_2,\ldots,A_k\}\).

Вправа\(\PageIndex{5.2}\)

Припустимо,\(n\) це вільне від квадратів число, тобто не\(m^2\) ділить число\(n\); по-іншому, числа без квадратів є добутками різних простих множників, тобто\(n=p_1p_2\cdots p_k\), де кожен з них\(p_i\) є простим і немає двох простих множників рівних. Знайти кількість факторизацій\(n\). Наприклад\(30=2\cdot 3\cdot 5\), і факторизації 30 складають 30,\(6\cdot 5\),\(10\cdot 3\)\(2\cdot 15\), і\(2\cdot 3\cdot 5\). Зверніть увагу, що ми вважаємо 30 поодинці як факторизацію, хоча в деякому сенсі тривіальну факторизацію.

Вправа\(\PageIndex{5.3}\)

Схема рими строфи поезії вказує, які рядки римуються. Зазвичай це виражається у формі ABAB, що означає перший і третій рядки чотирирядкової строфи рими, як це роблять другий і четвертий, або ABCB, що означають тільки рядки дві і чотири рими і так далі. Лімерик - це п'ятирядковий вірш зі схемою римування AABBA. Скільки різних схем рими можливо для\(n\) строфи рядка? Щоб уникнути дублювання візерунків, ми дозволяємо нову літеру лише тоді, коли всі попередні літери були використані зліва від нової. Наприклад, ACBA не допускається, так як при розміщенні C в положення 2, B не використовувався ліворуч. Це та ж схема рими, що і ABCA, яка допускається.

Вправа\(\PageIndex{5.4}\)

Інший спосіб висловити числа Белла для\(S(n,k)\) -\(n>0\) це\[B_n=\sum_{k=1}^n S(n,k),\nonumber\] де кількість\(\{1,2,\ldots,n\}\) розділів на точно\(k\) частини,\(1\le k\le n\). Це\(S(n,k)\) числа Стірлінга другого роду. Знайдіть зв'язок повторення для\(S(n,k)\). Ваше повторення має дозволити досить просту конструкцію трикутника, що містить значення\(S(n,k)\), а потім числа Белла можна обчислити шляхом підсумовування рядків цього трикутника. Покажіть перші п'ять рядів трикутника,\(n\in\{1,2,\ldots,5\}\).

Вправа\(\PageIndex{5.5}\)

\(A_n\)Дозволяти кількість розділів,\(\{1,2,\ldots,n+1\}\) в яких немає послідовних цілих чисел в одній частині розділу. Наприклад, коли\(n=3\) ці перегородки є\(\{\{1\},\{2\},\{3\},\{4\}\}\),\(\{\{1\},\{2,4\},\{3\}\}\),\(\{\{1,3\},\{2\},\{4\}\}\),\(\{\{1,3\},\{2,4\}\}\),\(\{\{1,4\},\{2\},\{3\}\}\), так\(A_3=5\). \(A(n,k)\)Дозволяти кількість\(\{1,2,\ldots,n+1\}\) розділів на точно\(k\) частини, в яких немає послідовних цілих чисел в одній частині розділу. Таким чином\[A_n=\sum_{k=2}^{n+1} A(n,k).\nonumber\] Знайдіть повторення,\(A(n,k)\) а потім покажіть, що\(A_n=B_n\).

1.6: Вибір з повторенням

Вправа\(\PageIndex{6.1}\)

Припустимо, що коробка містить 18 куль під номером 1—6, по три кульки з кожним номером. Коли 4 кулі намальовані без заміни, скільки результатів можливо? Робити це можна двома способами: припускаючи, що порядок, в якому малюються кулі, має значення, а потім припускаючи, що порядок не має значення.

Вправа\(\PageIndex{6.2}\)

Скільки перестановок букв у Міссісіпі?

Вправа\(\PageIndex{6.3}\)

Скільки існує перестановок мультимножини\(\{1\cdot a_1,1\cdot a_2,\ldots,1\cdot a_n\}\)?

Вправа\(\PageIndex{6.4}\)

Нехай\(M=\sum_{i=1}^n m_i\). Якщо\(k_i< 0\), скажімо\[ {M\choose k_1\;k_2\;\ldots\; k_n}=0.\nonumber\]

Доведіть, що\[{M\choose m_1\;m_2\;\ldots\; m_n}= \sum_{i=1}^n {M-1\choose m_1\;m_2\;\ldots\;(m_i-1)\;\ldots\; m_n}. \nonumber\]

Зверніть увагу, що коли\(n=2\) це стане\[{M\choose m_1\;m_2}= {M-1\choose (m_1-1)\;m_2}+{M-1\choose m_1\;(m_2-1)}.\nonumber\]

Як зазначалося вище в Equation (1.6.1), коли\(n=2\) ми дійсно бачимо звичайні біноміальні коефіцієнти, і це можна переписати як те,\[ {M\choose m_1}={M-1\choose m_1-1}+{M-1\choose m_1},\nonumber\] що, звичайно, ми вже знаємо.

Вправа\(\PageIndex{6.5}\)

Біноміальна теорема 1.4.1 може бути записана\[(x+y)^n=\sum_{i+j=n} {n\choose i\;j}x^i\,y^j,\nonumber\] там, де сума перевищує всі невід'ємні цілі числа\(i\) і\(j\) що сума до\(n\). Доведіть, що для\(m\ge 2\),\[ (x_1+x_2+\cdots+x_m)^n= \sum {n\choose i_1\;i_2\;\ldots\;i_m}x_1^{i_1}\,x_2^{i_2}\ldots x_m^{i_m}.\nonumber\] де сума закінчена всі\(i_1,\ldots,i_m\) такі, що\(i_1+\cdots+i_m=n\).

1.7: Принцип «голубиного отвору»

Вправа\(\PageIndex{7.1}\)

Припустимо, що відношення «друг» симетричне. Покажіть\(n\ge2\), що якщо, то в будь-якій групі\(n\) людей є двоє з однаковою кількістю друзів в групі.

Вправа\(\PageIndex{7.2}\)

Припустимо, що 501 різних цілих чисел вибрано з\(1\ldots1000\). Показати, що існують різні вибрані цілі числа\(a\) і\(b\) такі, що\(a | b\). Показати, що це не завжди вірно, якщо вибрано 500 цілих чисел.

Вправа\(\PageIndex{7.3}\)

Кожна з 15 червоних куль і 15 зелених кульок позначена цілим числом від 1 до 100 включно; на більш ніж одній кулі не з'являється ціле число. Значення пари кульок - це сума чисел на кульках. Показати є як мінімум дві пари, що складаються з одного червоного і одного зеленого кулі, з однаковим значенням. Покажіть, що це неправда, якщо є 13 кульок кожного кольору.

Вправа\(\PageIndex{7.4}\)

\((a_1,a_2,\ldots,a_{52})\)Припустимо, це цілі числа, не обов'язково відмінні. Покажіть, що їх два,\(a_i\) і\(a_j\) з\(i\ne j\), такі, що\(a_i+a_j\) або або\(a_i-a_j\) ділиться на 100. Показати, що це не обов'язково вірно для цілих чисел\((a_1,a_2,\ldots,a_{51})\).

Вправа\(\PageIndex{7.5}\)

Припустимо, п'ять точок обрані з квадрата, сторони якого - довжина\(s\). (Точки можуть бути як у внутрішній частині квадрата, так і на кордоні.) Покажіть, що дві точки знаходяться максимум\(s\sqrt2/2\) один від одного. Знайдіть п'ять точок так, щоб не було двох менше, ніж\(s\sqrt2/2\) один від одного.

Вправа\(\PageIndex{7.6}\)

Покажіть, що якщо краю\(K_6\) пофарбовані двома кольорами, є принаймні два однотонних трикутника. (Два трикутника різні, якщо кожен містить принаймні одну вершину, а не в іншій. Наприклад, два червоних трикутника, які поділяють ребро, вважаються двома трикутниками.) Розфарбуйте краю\(K_6\) так, щоб вийшло рівно два однотонних трикутника.

Вправа\(\PageIndex{7.7}\)

Припустимо, краю а\(K_5\) пофарбовані двома кольорами, скажімо червоним і синім, щоб не було однотонних трикутників. Покажіть, що червоні краї утворюють цикл, а сині краї утворюють цикл, кожен з яких має п'ять ребер. (Цикл - це послідовність ребер\(\{v_1,v_2\},\{v_2,v_3\},\ldots,\{v_k,v_1\}\), де всі\(v_i\) різні. Зверніть увагу, що це вірно на малюнку 1.7.1).

Вправа\(\PageIndex{7.8}\)

Покажіть, що\(8< R(3,4)\le 10\).

Вправа\(\PageIndex{7.9}\)

Покажіть, що\(R(3,4)=9\).

1.8: Теорема Спернера

Вправа\(\PageIndex{8.1}\)

Теорема Спернера (1.8.1) говорить нам\(\left[\begin{array}{c}6\\3\end{array}\right]\), що з розміром 20 є унікальним найбільшим анти-ланцюгом для\(2^{[6]}\). Наступними найбільшими анти-ланцюгами форми\(\left[\begin{array}{c}6\\k\end{array}\right]\) є\(\left[\begin{array}{c}6\\2\end{array}\right]\) і\(\left[\begin{array}{c}6\\4\end{array}\right]\), з розміром 15. Знайдіть максимальну анти-ланцюг розміром більше 15, але менше 20. (Як завжди, максимальний тут означає, що анти-ланцюг не можна збільшити, просто додаючи елементи. Таким чином, ви не можете просто використовувати підмножину\(\left[\begin{array}{c}6\\3\end{array}\right]\).)

1.9: Числа Стірлінга

Вправа\(\PageIndex{9.1}\)

Знайдіть простий вираз для\(\left[\begin{array}{c}n\\n-1\end{array}\right]\).

Вправа\(\PageIndex{9.2}\)

Знайдіть простий вираз для\(\left[\begin{array}{c}n\\1\end{array}\right]\).

Вправа\(\PageIndex{9.3}\)

Що таке\(\sum_{k=0}^n \left[\begin{array}{c}n\\k\end{array}\right]\)?

Вправа\(\PageIndex{9.4}\)

Що таке\(\sum_{k=0}^n s(n,k)\)?

Вправа\(\PageIndex{9.5}\)

Показати\(x^{\underline n}=\prod_{k=0}^{n-1}(x-k)=\sum_{i=0}^n s(n,i)x^i\), що,\(n\ge 1\);\(x^{\underline n}\) називається падаючим факторіалом. Знайти подібну ідентичність для\(x^{\overline n}=\prod_{k=0}^{n-1}(x+k)\);\(x^{\overline n}\) є зростаючим факторіалом.

Вправа\(\PageIndex{9.6}\)

Показати\( \sum_{k=0}^n \left\{\begin{array}{c}n\\k\end{array}\right\} x^{\underline k} = x^n\), що,\(n\ge 1\);\(x^{\underline k}\) визначено в попередній вправі. Попередня вправа показує, як висловити падіння факторіал з точки зору повноважень\(x\); ця вправа показує, як висловити повноваження з\(x\) точки зору падіння факторіалів.

Вправа\(\PageIndex{9.7}\)

Доведіть:\( S(n,k)=\sum_{i=k-1}^{n-1} {n-1\choose i}S(i,k-1)\).

Вправа\(\PageIndex{9.8}\)

Доведіть:\( \left[\begin{array}{c}n\\k\end{array}\right]=\sum_{i=k-1}^{n-1} (n-i-1)! {n-1\choose i}\left[\begin{array}{c}i\\k-1\end{array}\right]\).

Вправа\(\PageIndex{9}\)

Використовуйте попередню вправу, щоб довести\( s(n,k)=\sum_{i=k-1}^{n-1} (-1)^{n-i-1}(n-i-1)! {n-1\choose i}s(i,k-1)\).

Вправа\(\PageIndex{10}\)

Ми визначили\(\left[\begin{array}{c}n\\k\end{array}\right]\) і\(\left\{\begin{array}{c}n\\k\end{array}\right\}\) для\(n,k\ge 0\). Ми хочемо розширити визначення до всіх цілих чисел. Без якихось зайвих умов існує безліч способів зробити це. Давайте припустимо, що для\(n\not=0\) ми хочемо\(\left[\begin{array}{c}n\\0\end{array}\right]=\left[\begin{array}{c}0\\n\end{array}\right]=\left\{\begin{array}{c}n\\0\end{array}\right\}=\left\{\begin{array}{c}0\\n\end{array}\right\}=0\), і ми хочемо рекуррентні відносини рівняння 1.9.1 і в теоремі 1.9.1, щоб бути істинним. Показати, що за цих умов існує унікальний спосіб розширити визначення на всі цілі числа, і що коли це буде зроблено,\(\left\{\begin{array}{c}n\\k\end{array}\right\}=\left[\begin{array}{c}-k\\-n\end{array}\right]\) для всіх цілих чисел\(n\) і\(k\). Таким чином, розширена таблиця значень для\(\left[\begin{array}{c}n\\k\end{array}\right]\) або або\(\left\{\begin{array}{c}n\\k\end{array}\right\}\) буде містити всі значення обох\(\left[\begin{array}{c}n\\k\end{array}\right]\) і\(\left\{\begin{array}{c}n\\k\end{array}\right\}\).

Вправа\(\PageIndex{11}\)

За припущеннями\(n\not=0\), що\(s(n,0)=s(0,n)=0\) for\(s(n,k) = s(n-1,k-1) - (n-1)s(n-1,k)\), і, розширити таблицю для\(s(n,k)\) всіх цілих чисел, і знайти зв'язок\(S(n,k)\) подібне до того, що в попередній задачі.

Вправа\(\PageIndex{12}\)

Доведіть наслідок 1.9.1.

Вправа\(\PageIndex{13}\)

Доведіть решту теореми 1.9.2.