1.7: Принцип голубиного отвору

Ключовий крок у багатьох доказах полягає у тому, щоб показати, що два, можливо, різні значення насправді однакові. У цьому іноді може допомогти принцип Pigeonhole.

Теорема \(\PageIndex{1}\): Pigeonhole Principle

Припустимо, що\(n+1\) (або більше) предметів поміщають в\(n\) ящики. Тоді якась скринька містить щонайменше два об'єкти.

Доказ

Припустимо, кожне поле містить не більше одного об'єкта. Тоді загальна кількість об'єктів - це максимум\(1+1+\cdots+1=n\), протиріччя.

Цей, здавалося б, простий факт може бути використаний дивовижними способами. Ключ, як правило, полягає в тому, щоб покласти об'єкти в коробки відповідно до деякого правила, так що коли два об'єкти потрапляють в одне і те ж поле, це тому, що вони мають певні бажані відносини.

Приклад\(\PageIndex{1}\):

Серед будь-яких 13 осіб щонайменше два поділяють місяць народження.

Позначте 12 коробок з назвами місяців. Покладіть кожну людину в коробку, позначену його місяцем народження. Якась коробка міститиме щонайменше двох людей, які поділяють місяць народження.

Приклад\(\PageIndex{2}\):

Припустимо, 5 пар шкарпеток знаходяться в ящику. Підбір 6 шкарпеток гарантує, що буде обрана хоча б одна пара.

Позначте коробки «парами» (наприклад, червона пара, синя пара, пара аргайла,...). Покладіть 6 шкарпеток в коробки відповідно до опису.

Деякі використання цього принципу не настільки прості.

Приклад\(\PageIndex{3}\)

\(a_1,\ldots,a_n\)Припустимо, цілі числа. Тоді деяка «послідовна\(a_k+a_{k+1}+a_{k+2}+\cdots+a_{k+m}\) сума» ділиться на\(n\).

Розглянемо ці\(n\) суми:\[\eqalign{ s_1&=a_1\cr s_2&=a_1+a_2\cr s_3&=a_1+a_2+a_3\cr &\vdots\cr s_n&=a_1+a_2+\cdots+a_n\cr }\nonumber\]

Це всі послідовні суми, тому, якщо одна з них ділиться на\(n\) ми закінчимо. Якщо ні, ділення кожного на\(n\) залишає ненульовий залишок\(r_1=s_1\bmod n\)\(r_2=s_2\bmod n\), і так далі. Ці залишки мають значення в\(\{1,2,3,\ldots,n-1\}\). Позначте\(n-1\) коробки з цими\(n-1\) значеннями; покладіть кожну з\(n\) сум у поле, позначене його модом залишку\(n\). Дві суми закінчуються в одному полі, що означає, що\(s_i\bmod n=s_j\bmod n\) для деяких\(j>i\); отже,\(s_j-s_i\) ділиться на\(n\), і\(s_j-s_i=a_{i+1}+a_{i+2}+\cdots+a_j\), за бажанням.

Подібний аргумент дає доказ китайської теореми про залишок.

Теорема \(\PageIndex{2}\): Chinese Remainder Theorem

Якщо\(m\) і відносно\(n\) прості,\(0\le a< m\) і\(0\le b< n\), то існує ціле число\(x\) таке, що\(x\bmod m=a\) і\(x\bmod n=b\).

Доказ

Розглянемо цілі числа\(a,a+m,a+2m,\ldots a+(n-1)m\), кожне з залишком\(a\) при діленні на\(m\). Ми хочемо показати, що одне з цих цілих чисел має залишок\(b\) при діленні на\(n\), і в цьому випадку це число задовольняє бажану властивість.

За протиріччя припустимо, що ні. Нехай залишки будуть\(r_0=a\bmod n\),\(r_1=a+m\bmod n\),...,\(r_{n-1}=a+(n-1)m\bmod n\). Позначте\(n-1\) коробки з цифрами\(0,1,2,3,\ldots,b-1,b+1,\ldots n-1\). Покладіть кожен\(r_i\) в коробку з позначкою зі своїм значенням. Два залишки закінчуються в одній коробці, скажімо\(r_j\),\(r_i\) і, з\(j>i\), так\(r_i=r_j=r\). Це означає, що\[a+im=q_1n+r\quad\hbox{and}\quad a+jm=q_2n+r.\nonumber\]

Звідси\[\eqalign{ a+jm-(a+im)&=q_2n+r-(q_1n+r)\cr (j-i)m&=(q_2-q_1)n.\cr }\nonumber\]

Оскільки\(n\) є відносно простим\(m\), це означає, що\(n | (j-i)\). Але так як\(i\) і\(j\) знаходяться в\(\{0,1,2,\ldots,n-1\}\)\(0< j-i< n\), так\(n\cancel{|}(j-i)\). Це протиріччя закінчує доказ.

Більш загальні версії принципу Pigeonhole можуть бути доведені по суті тим же методом. Природне узагальнення було б приблизно таким: Якщо\(X\) об'єкти поміщені в\(n\) коробки, якась коробка містить принаймні\(m\) предмети. Наприклад:

Теорема \(\PageIndex{3}\)

Припустимо, що\(r_1,\ldots,r_n\) є додатними цілими числами. Якщо\(X\ge(\sum_{i=1}^n r_i) -n + 1\) об'єкти поміщаються в позначені\(n\) поля\(1,2,3,\ldots,n\), то деякі поля з міткою\(i\) містять принаймні\(r_i\) об'єкти.

Доказ

Припустимо, що ні. Тоді загальна кількість предметів в ящиках - максимум\((r_1-1)+(r_2-1)+(r_3-1)+\cdots+(r_n-1)=(\sum_{i=1}^n r_i) -n < X\), протиріччя.

Таке повне узагальнення потрібно лише зрідка; часто достатньо цього більш простого варіанту:

Слідство \(\PageIndex{1}\)

Припустимо,\(r>0\) і\(X\ge n(r-1)+1\) предмети поміщаються в\(n\) ящики. Тоді якась коробка містить принаймні\(r\) об'єкти.

Доказ

Застосовуйте попередню теорему з\(r_i=r\) для всіх\(i\).

\[\bullet\quad\bullet\quad\bullet\nonumber\]

Ось просте застосування принципу Pigeonhole, що призводить до багатьох цікавих питань.

Приклад\(\PageIndex{4}\)

Припустимо, 6 чоловік зібрані разом; тоді або 3 з них взаємно знайомі, або 3 з них взаємно незнайомі.

Ми перетворюємо це на питання теорії графів: Розглянемо граф, що складається з 6 вершин, кожна з яких з'єднана з усіма іншими ребром, називається повним графом по\(6\) вершинам, і позначається\(K_6\); вершини представляють людей. Пофарбуйте край червоним, якщо люди, представлені його кінцевими точками, знайомі, і синім, якщо вони не знайомі. Будь-який вибір з 3 вершин визначає трикутник; ми хочемо показати, що або є червоний трикутник, або синій трикутник.

Розглянемо п'ять ребер, що падають на одну вершину\(v\); за принципом Pigeonhole (версія у слідстві 1.6.7\(r=3\), з,\(X=2(3-1)+1=5\)), принаймні три з них є одним кольором, називайте його кольором\(C\); називайте інший колір\(D\). Нехай вершини на інших кінцях цих трьох ребер be\(v_1\),\(v_2\),\(v_3\). Якщо будь-яке з ребер між цими вершинами має колір\(C\), виникає трикутник кольору\(C\): якщо ребро з'єднується\(v_i\) з\(v_j\), трикутник утворюється шляхом\(v\)\(v_i\), і\(v_j\). Якщо це не так, то три вершини\(v_1\)\(v_2\),\(v_3\) з'єднуються краями кольору\(D\), і утворюють трикутник кольору\(D\).

Число 6 у цьому прикладі особливе: з 5 або меншими вершинами неправда, що повинен бути однотонний трикутник, а з більш ніж 6 вершинами це правда. Щоб побачити, що це не вірно для 5 вершин, нам потрібно лише показати приклад, як на рис\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Забарвлення краю без однотонних трикутників.

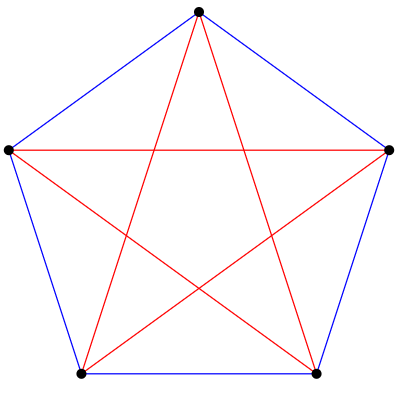
Число Рамсі\(R(i)\) є найменшим цілим числом\(n\) таким чином, що коли ребра\(K_n\) пофарбовані двома кольорами, існує монохроматичний повний граф по\(i\) вершинам\(K_i\), що міститься всередині\(K_n\). Приклад показує, що\(R(3)=6\).

More generally, \(R(i,j)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with two colors, say \(C_1\) and \(C_2\), either there is a \(K_i\) contained within \(K_n\) all of whose edges are color \(C_1\), or there is a \(K_j\) contained within \(K_n\) all of whose edges are color \(C_2\). Using this notion, \(R(k)=R(k,k)\). More generally still, \(R(i_1,i_2,\ldots,i_m)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with \(m\) colors, \(C_1,…,C_m\), then for some \(j\) there is a \(K_{i_j}\) contained in \(K_n\) all of whose edges are color \(C_j\).

Ramsey proved that in all of these cases, there actually is such a number \(n\). Generalizations of this problem have led to the subject called Ramsey Theory.

Computing any particular value \(R(i,j)\) turns out to be quite difficult; Ramsey numbers are known only for a few small values of \(i\) and \(j\), and in some other cases the Ramsey number is bounded by known numbers. Typically in these cases someone has exhibited a \(K_m\) and a coloring of the edges without the existence of a monochromatic \(K_i\) or \(K_j\) of the desired color, showing that \(R(i,j)>m\); and someone has shown that whenever the edges of \(K_n\) have been colored, there is a \(K_i\) or \(K_j\) of the correct color, showing that \(R(i,j)\le n\).

Contributors and Attributions

• Template:ContribGuichard