23.1: Біономіальні коефіцієнти
- Page ID
- 65281
вираз виду\((x + y)^n\text{,}\) де\(n \in \mathbb{N}\) і\(x,y\) є дійсними числами (або елементами будь-якого комутативного кільця з ідентичністю)
Розширення біноміалів ускладнюється зі\(n\) збільшенням.
\ почати {вирівнювати*} (х + у) ^2 & = x^2+ 2 х y+ y^2\\ (х + у) ^3 & = (х + у) (x^2+ 2 x y+ y^2) = x^3+ x ^2 y + 3 х y^2 + y^3\\ (x + y) ^4 & = (x + y) (x + y) 3 + 3 х ^ 2 у + 3 х х х ^ 2 + у ^ 3) = х ^ 4 х ^ 3 у + 6 х ^2 + 4 х х х ^ 3 + у ^ 4\\ (х + у) ^5 & = (х + у) (х + у) (х ^ 4 х ^ 3 у + 6 х ^ 2 у ^ 2 + 4 х х х ^3 + y^3 + y^4)\ amp; = x^5 + 5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 x y^4 + y^5\\ &\ vdots\ end {align*}
Симетрія в кожному з цих розширень слід очікувати: ми отримаємо той самий вираз у протилежному порядку підсумовування, якщо ми поміняли місцями\(x\) і\(y\text{,}\) з тих пір\((x + y)^n = (y + x)^n\text{.}\)
число, що з'являється як коефіцієнт в розширенні\((x + y)^n\)
\(k^{th}\)коефіцієнт в розширенні\((x + y)^n\) (\(0 \le k \le n\))
Щоб краще зрозуміти складність біноміальних розширень, нам слід шукати та експлуатувати закономірності. Ми вже розширили деякі біноміальні вирази для малих показників у прикладі\(\PageIndex{1}\) — давайте витягнемо біноміальні коефіцієнти з цих виразів.
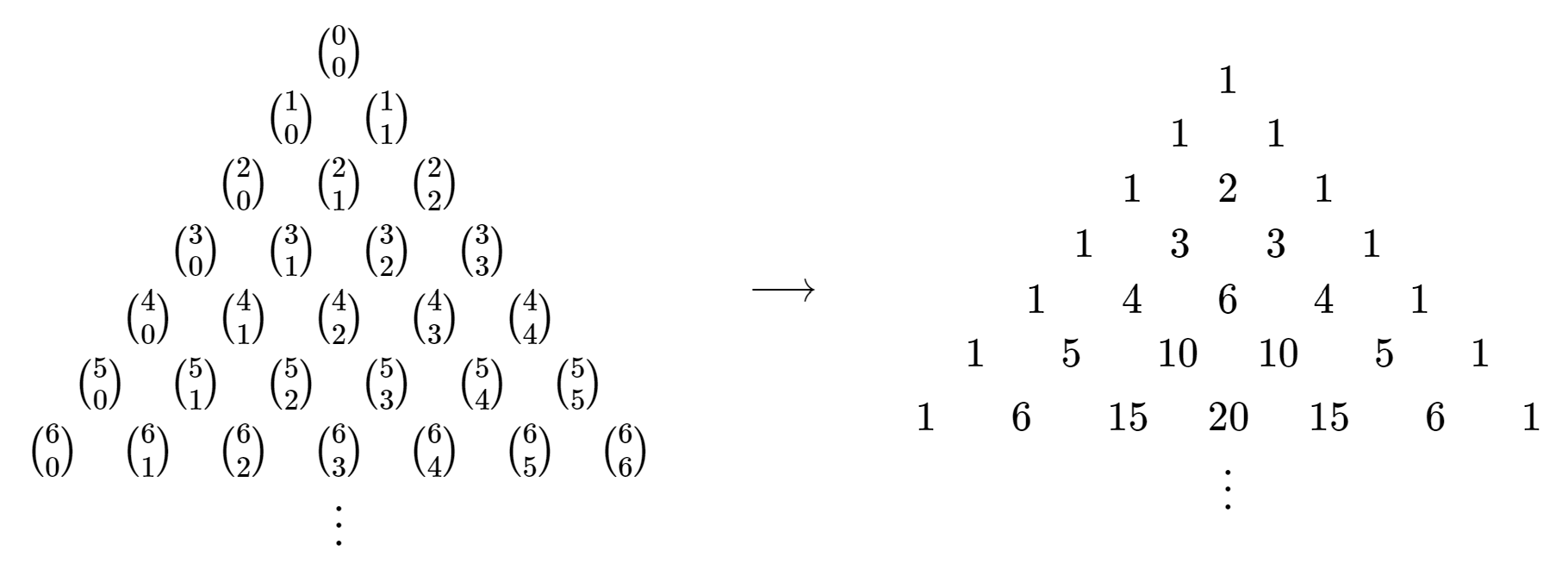
Малюнок\(\PageIndex{1}\) вище впевнений, що виглядає так само, як Малюнок 22.4.1.
Для кожного\(x,y\in\mathbb{R}\) у\(n \in \mathbb{N}\text{,}\) нас є
\ begin {рівняння*} (x+y) ^n =\ sum_ {k=0} ^n\ біном {n} {k}\, x^ {n-k} y^k =\ біном {n} {0}\, x^n +\ біном {n} {1}\, x^ {n-1} y +\ binom {n} {2}, x^ {x^ n-2} y^2 +\ cdots +\ binom {n} {n-1}\, xy^ {n-1} +\ binom {n}\, y^n,\ end {рівняння*}
де
\ begin {рівняння*}\ біном {n} {k} = C^n_k =\ dfrac {n!} {k! (н-к)!} \ текст {.} \ end {рівняння*}
- Неформальний прямий контур доказу.
-
Пишіть\((x+y)^n = (x+y)(x+y)\cdots(x+y)\text{,}\) з\(n\) факторами. Щоб розширити це, ми узагальнюємо метод FOIL: з кожного фактора вибирайте\(x\) або\(y\text{,}\) потім помножте всі ваші варіанти разом. Потім додайте результати всіх можливих подібних продуктів. Наприклад,
\ почати {вирівнювати*} (х + у) ^ 2 & = х х х х х й+ у х + у = х ^ 2 х у + у ^ 2 х у ^ 2,\\ (х + у) ^3 & = х х х х х х х х х х х х х х х х х х х х х х х х х х у + у х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х х y^2+ y^3. \ end {align*}
При формуванні певного продукту, якщо ви\(k\) вибрали\(y\) для інших\(n\) варіантів, ви повинні були\(x\) обрати\(n - k\) решту\(n\) варіантів. Результат буде\(x^{n - k} y^k\text{.}\) Таким чином, щоб з'ясувати коефіцієнт на\(x^{n - k} y^k\text{,}\) просто порахуйте, скільки способів є вибрати\(y\) для\(k\)\(n\) вибору. Це саме те\(C^n_k\text{,}\), де ми вибираємо\(k\) фактори,\((x+y)\) щоб дати нам\(y\text{,}\) а решту, щоб дати нам\(x\text{.}\)
- Індукційний контур доказ.
-
Базовий кейс.
\(n=0,1\)Випадки банально вірні.Індукційний крок.
Використовуйте біноміальну формулу\((x+y)^{n - 1}\) для отримання біноміальної\((x + y)^n\text{,}\) формули для маніпуляцій\ почати {вирівнювати*} (х + у) ^n & = (х + у) (х + у) ^ {n - 1}\\ & = (x + y) (С^ {n-1} _0\, x^ {n - 1} + С^ {n-1} _1\, x^ {n - 2} y +\ cdots + C^ {n-1} _ {n-1}\, y^ {n - 1})\ текст {.} \ end {вирівнювати*}
Розгорнути\((x-2)^5\text{.}\)
Рішення
Ми побачили, що\(n = 5\) ряд трикутника Паскаля\(1,5,10,10,5,1\text{.}\)
\ begin {align*} & (x - 2) ^5\\ & (x + (- 2)) ^5\\ & =\ біном {5} {0} x^5 +\ binom {5} {1} x^4 (-2) +\ binom {5} {2} x^3 (-2) ^2 +\ binom {5} {3} x^2 (-2) ^2 3 +\ біном {5} {4} х (-2) ^4 +\ біном {5} {5} (-2) ^5\\ & = x^5 - 10 х^4 + 40 х^3 - 80 х ^ 2 + 80 х - 32. \ end {вирівнювати*}
Який коефіцієнт на\(x^4 y^9\) термін при розширенні\((3 x + y)^{13} \text{?}\)
Рішення
Враховуючи
\ begin {рівняння*} (3 x + y) ^ {13} = (((3 x) + y) ^ {13}\ текст {,}\ end {рівняння*}
\(x^4 y^9\) термін дорівнює
\ begin {вирівнювати*}\ біном {13} {9} (3x) ^4 y^9 & =\ dfrac {13!} {9! 4!} \ крапка 3 ^ 4 х ^ 4 y^9\\ & =\ dfrac {13\ cdot 12\ dot 1\ точка 10\ точка 27\ точка 3} {4\ cdot 3\ cdot 2} x^4 y^9\\ & = (13\ cdot 3\ cdot 1\ cdot 5\ cdot 27) x^4 y^9\ text {. \ end {align*}
Отже, бажаний коефіцієнт\(57,915\text{.}\)
