13.1: Основи та приклади
- Page ID
- 64900
Якщо\(A\) це набір, який має такий же розмір, як\(\mathbb{N}\text{,}\) тоді ми можемо думати про біекцію\(\mathbb{N} \to A\) як «підрахунок» елементів\(A\) (хоча існує нескінченна кількість елементів для підрахунку), точно так само, як ми використовуємо наші підрахункові набори\(\mathbb{N}_{<m}\) для підрахунку скінченних множин.
набір, який є кінцевим або має такий же розмір, як\(\mathbb{N}\)
обчислювальний набір, який має такий же розмір, як\(\mathbb{N}\)
набір, який не підлягає підрахунку
- Незліченний набір обов'язково нескінченний.
- Два множини, які мають однаковий розмір (тобто існує біекція між ними) є або підрахунковими, або обидва незліченними.
Непорожній набір\(A\) підлягає підрахунку тоді і лише тоді, коли існує послідовність елементів, з\(A\) яких кожен елемент\(A\) з'являється рівно один раз.
- Доказ ідеї.
-
У випадку\(A\) є кінцевим, твердження є саме тим фактом 12.2.1. Отже, припустимо,\(A\) нескінченно, і в цьому випадку послідовність типу, описаного в операторі, також повинна бути нескінченною. Технічно нескінченна послідовність від\(A\) - це функція\(\mathbb{N} \to A\text{.}\) Властивість «кожен елемент\(A\)» така ж, як сказати, що функція є суб'єктивною, а властивість «точно один раз» така ж, як сказати, що функція є ін'єкційною. Таким чином, послідовність описаного роду точно така ж, як біекція,\(\mathbb{N} \to A\text{,}\) яка є те, що потрібно для того,\(A\) щоб бути таким же розміром, як\(\mathbb{N}\) (тобто незліченно нескінченно)
Порівняйте цей факт з Фактом 12.2.1.
Набори\(\mathbb{Z}\) і\(\mathbb{Q}\) обидва підраховуються.
- Доказ
-
Ми вже побудували біекцію\(\mathbb{N} \to \mathbb{Z}\) в прикладі 12.3.1, який показує, що\(\mathbb{Z}\) підраховується.
Щоб показати, що\(\mathbb{Q}\) підраховується, ми будемо використовувати факт\(\PageIndex{1}\) і побудувати нескінченну послідовність, яка містить кожен елемент\(\mathbb{Q}\) рівно один раз. Спочатку побудуйте нескінченну сітку, яка містить всі позитивні раціональні числа. За допомогою зиг-заґінгу через сітку ми отримуємо нескінченну послідовність, яка містить кожен позитивний елемент\(\mathbb{Q}\) принаймні один раз, хоча є дублікати, оскільки елемент\(\mathbb{Q}\) може мати багато різних уявлень у вигляді дробу.

Малюнок\(\PageIndex{1}\): Сітка, що містить всі позитивні раціональні числа. 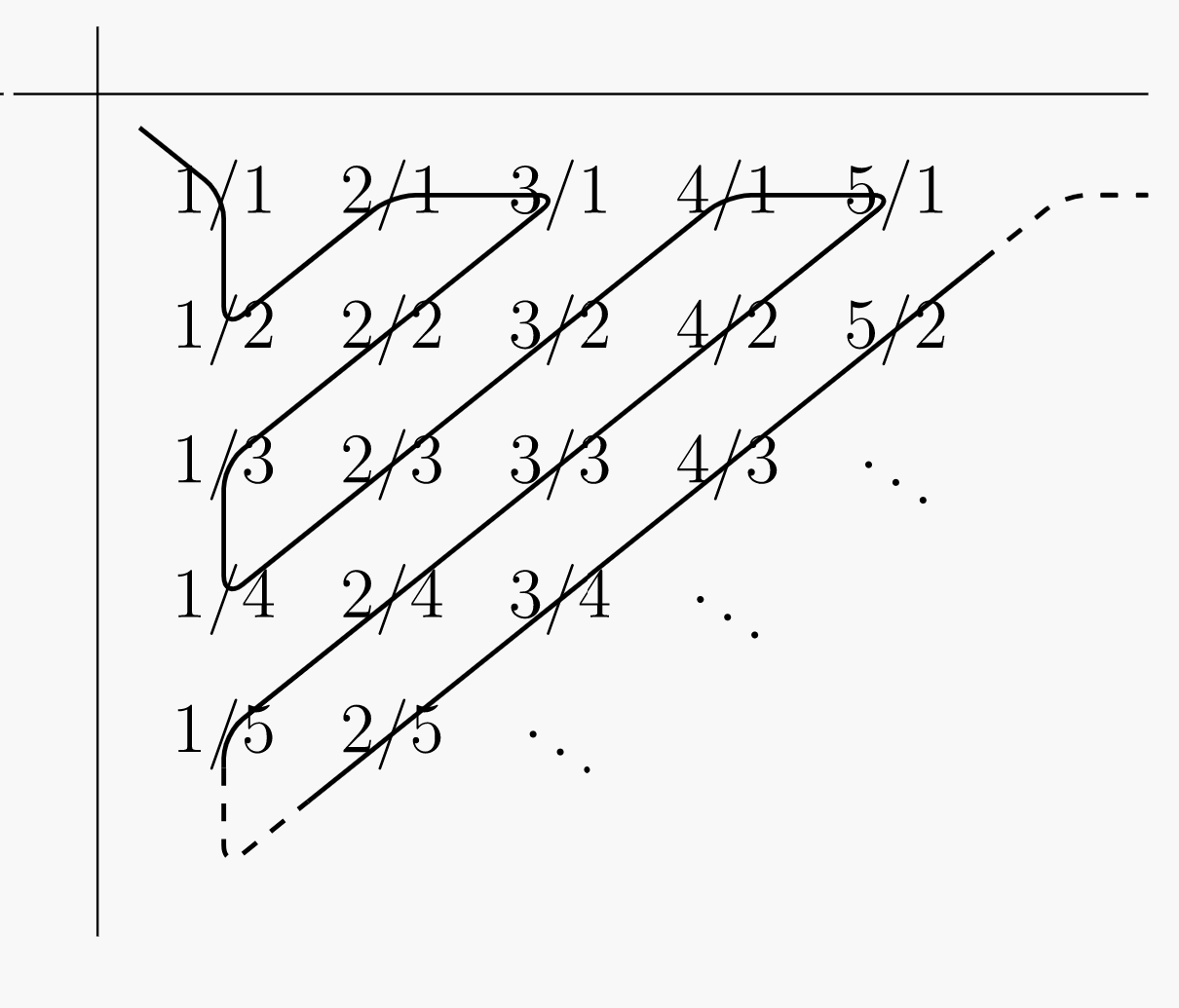
Малюнок\(\PageIndex{2}\): Шляхи через позитивні раціональні числа. Шляхом через сітку створюється наступна послідовність позитивних раціональних чисел. Викреслюючи дублікати, ми отримуємо нескінченну послідовність, яка містить кожне додатне раціональне число рівно один раз.
\ begin {збирати*} 1,\;\;\;\ dfrac {1} {2},\;\; 2,\;\;\; 3,\;\;\;\;\;\ cancel {1}\;\;\;\;\;\;\;\ dfrac {2} {3},\;\;\;\ dfrac {3} {2},\;\; 4,\;\;\; 5,\\ cancel {2}\;\;\;\ cancel {1,}\;\;\; скасувати {\ dfrac {1} {2},}\;\;\;\;\ dfrac {1} {5},\;\;\;\ dfrac {1} {6},\;\;\;\ dfrac {2} {5},\ ;\;\;\ dfrac {3} {4},\;\;\;\;\ dfrac {4} {3},\;\;\;\ dfrac {5} {2},\;\;\;\ dotsc\ end {збори*}Нарешті, чергуйте від'ємні раціональні числа у наведену вище послідовність та вставте\(0\) на початку.
\ begin {збирати*} 0,\;\;\; 1,\;\;\; -1,\;\;\;\ dfrac {1} {2},\;\;\; -\ dfrac {1} {2},\;\;\; 2,\;\;\; -2,\;\;\; 3,\;\; -3,\;\;;\;\ dfrac {1} {3},\;\;\; -\ dfrac {1} {3},\;\;\\ dfrac {1} {4},\;\;\; -\ dfrac {1} {4},\;\;\;\;\ dfrac {2} {3},\;\;\;\;\; dfrac {2} {3},\;\;\;\;\ dfrac {3} {2},\;\;\; -\ dfrac {3} {2},\;\;\;\; 4,\;\;\;\;\ ; -4,\;\;\;\; 5,\;\;\;\; -5,\;\;\;\ dotsc\ end {збирати*}
Ось приклад незліченного набору. Аргумент довести, що набір є незліченним, є відомим, тому ми інкапсулюємо його як доказ леми, а не просто простий приклад.
\(\scr{C}\)Дозволяти представляти множину всіх дійсних чисел між\(0\) і\(0.2\) (включаючи\(0\)) чиї десяткові розширення включають тільки цифри\(0\) і\(1\text{.}\)
Набір\(\scr{C}\) незліченний.
- Доказ
-
Аргумент у цьому доказі називається діагональним аргументом Кантора.
Ми покажемо, що жодна послідовність чисел з не\(\scr{C}\) може містити кожен елемент\(\scr{C}\text{.}\)
Припустимо,\(\{a_k\}\) це нескінченна послідовність елементів\(\scr{C}\text{.}\) Ми можемо створити елемент\(r \in \scr{C}\), який не знаходиться в послідовності наступним чином. Набір
\ begin {рівняння*} r = 0.r_1 r_2 r_3 r_4\ cdots\ text {,}\ end {рівняння*}
де\(r_k\) знаходиться цифра в\(k^{th}\) десятковому розряді за наступними правилами.\(r\text{,}\)Якщо встановлено\(k^{th}\)\(a_{k-1}\)\(0\text{,}\) десятковий знак\(r_k = 1\text{.}\)
Якщо встановлено\(k^{th}\)\(a_{k-1}\)\(1\text{,}\) десятковий знак\(r_k = 0\text{.}\)
Зрозуміло, що кожна цифра\(r\) буде\(0\) або\(1\text{,}\) а або\(0 \le r \lt 0.2\text{,}\) так\(r \in \scr{C}\text{.}\) (Причина, яку ми використовуємо\(a_{k-1}\) замість\(a_k\) правил, щоб створити\(r\), щоб переконатися, що ми розглянемо послідовність елемента\(a_0\) десь там.)
Тепер у нас є\(a_k \ne r\) для кожного\(k \in \mathbb{N}\text{,}\) з тих пір\(r\) і\(a_k\) відрізняються в\((k+1)^{th}\) десятковому розряді. Крім того,\(r \in \scr{C}\) оскільки воно між\(0\) і\(0.2\) і його десяткове розширення включає лише цифри\(0\) і\(1\text{.}\) тому послідовність\(\{a_k\}\) не містить кожного елемента,\(\scr{C}\) оскільки вона не містить\(r\text{.}\)
- «Діагональна» частина назви діагонального аргументу Кантора посилається на наступне. Якщо десяткові розширення дійсних чисел у послідовності\(\{a_k\}\) записуються в сітку так, що кожен рядок є одним з чисел,\(a_k\) а кожен стовпець представляє певний десятковий знак у порядкових числах, то правила для створення\(r\) можна розглядати як «перегортання» цифр, які відбуваються в діагональних положеннях цієї сітки. (Намалюйте сітку для себе, щоб побачити візерунок!)
- Пізніше в цьому розділі ми будемо використовувати Lemma,\(\PageIndex{1}\) щоб довести, що\(\mathbb{R}\) сама по собі незліченна. (Див. Теорему 13.2.1.)
