1.5: Конгруенції

Last updated
Save as PDF

Page ID: 105469

Leo Moser
University of Alberta via The Trilla Group

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми розробимо деякі аспекти теорії подільності та конгруенцій.

Якщо

$a = \prod p^{\alpha}$і$b = \prod p^{\beta}$

то легко помітити, що

$(a, b) = \prod p^{\text{min}(\alpha, \beta)}$в той час як$[a, b] = \prod p^{\text{max} (\alpha, \beta)}.$

З них легко випливає, що$(a, b) \cdot [a, b] = a \cdot b$. Ми залишаємо це як вправу, щоб показати, що

$(a, b) = \dfrac{1}{a} \sum_{a = 1}^{a - 1} \sum_{\beta = 1}^{a - 1} e^{2\pi i \dfrac{b}{a} \alpha \beta}.$

Позначення$a \equiv b$ (мод$m$) для$m\ |\ (a - b)$ обумовлено Гауссом. Досить очевидними властивостями цієї конгруентності є$a \equiv a$$a \equiv b \Rightarrow b \equiv a$,$a \equiv b$ і$b \equiv c \Rightarrow a \equiv c$, тобто,$\equiv$ є співвідношенням еквівалентності. Також легко доведено, що$a \equiv b$ і$c \equiv d$ разом мають на увазі$ac \equiv bd$; зокрема$a \equiv b \Rightarrow ka \equiv kb$. Однак зворотне в цілому не відповідає дійсності. Таким чином$2 \times 3 = 4 \times 3$ (мод 6) не має на увазі$2 \equiv 4$ (мод 6). Однак, якщо що$(k, m) = 1$$ka \equiv kb$ має на увазі$a \equiv b$.

Ще один важливий результат полягає в наступному.

Теорема

Якщо$a_1, a_2, ..., a_{\varphi(m)}$ сформувати повну систему залишку мод,$m$ то це робить$aa_1$,$aa_2$,...,$aa_{\varphi(m)}$ за умови$(a, m) = 1$.

Доказ: У нас є$\varphi(m)$ залишки. Якщо два з них є конгруентними$aa_i \equiv aa_j$,$a(a_i - a_j) \equiv 0$. Але$(a, m) = 1$ так що$a_i \equiv a_j$.

Застосування цих ідей до важливої теореми Ейлера:

Теорема

Якщо$(a, m) = 1$ тоді$a^{\varphi(m)} \equiv 1$ (мод$m$).

Доказ

Оскільки$a_1, a_2, ..., a_{\varphi(m)}$ вони конгруентні$aa_1$,$aa_2$,...,$aa_{\varphi(m)}$ впевному порядку, їх продукція є конгруентною. Звідси

$a^{\varphi(m)} a_1 a_2 \cdot\cdot\cdot a_{\varphi(m)} \equiv a_1 a_2 \cdot\cdot\cdot a_{\varphi(m)}$

і результат випливає.

Особливим випадком першочергового значення є той випадок$m = p$, коли ми маємо

$(a, p) = 1 \Longrightarrow a^{p - 1} \equiv 1$(мод$p$)

Множення на$a$ ми маємо для всіх випадків$a^p \equiv a$ (мод$p$). Ще одним доказом цього результату є індукція$a$; у нас є

$(a + 1)^p = a^p + {p \choose 1} a^{p - 1} + \cdot\cdot\cdot + 1 \equiv a^p \equiv a$(мод$p$)

Можна також використовувати багатономіальну теорему і розглянути$(1 + 1 + \cdot\cdot\cdot + 1)^p$.

Ще одним доказом є, враховуючи кількість правильних опуклих$p$ -кутників, де кожен край може бути пофарбований в один з кольорів. Число таких багатокутників є$a^p$, з яких a однотонні. Отже$a^p − a$, вони не однотонні, і вони приходять у набори$p$ кожного шляхом обертання через$\dfrac{2\pi n}{p}, n = 1,2, ..., p−1$. Ідея, що стоїть за цим доказом, має значну застосовність, і ми повернемося принаймні до однієї іншої програми трохи пізніше. Ми також залишаємо в якості вправи завдання знайти аналогічний доказ теореми Ейлера.

Теореми Ферма та Ейлера також можна зручно розглядати з теоретико-групової точки зору. Цілі числа відносно прості$m$ та$< m$ утворюють групу під модом множення$m$. Головне тут перевірити, щоб кожен елемент мав зворотний в системі. Якщо ми шукаємо зворотне для a ми формуємо$aa_1, aa_2, ..., aa_{\varphi(m)}$. Ми вже бачили, що це$\varphi(m)$ числа непоєднувані мод$m$ і відносно прості до$m$. При цьому однією з них повинна бути одиниця і результат випливає.

Тепер ми повертаємо доказ Ейлера з лагранжа, який стверджує, що якщо$a$ є$G$ елементом групи порядку$m$, то$a^m = 1$. У нашому випадку це означає$a^{\varphi(m)} \equiv 1$ або$a^{p−1} \equiv 1$ якщо$p$ є простим.

Цілі числа$p$ утворюють поле відносно + і$\times$. Багато з важливих результатів теорії чисел засновані на тому, що мультиплікативна частина цієї групи (містить$p − 1$ елементи) є циклічною, тобто існує число$g$ (зване примітивним коренем$p$) таке, що$1 = g^0, g^10,g^2, ... , g^{p−1}$ є неконгруентним модом$p$. Цей факт не є тривіальним, але ми опускаємо докази. Більш загальний груповий теоретичний результат, в якому він міститься, стверджує, що кожне скінченне поле автоматично є абелевим, а його мультиплікативна група циклічна.

У кільці многочленів з коефіцієнтами в полі тримається багато теорем елементарної теорії рівнянь. Наприклад, якщо$f(x)$ є поліном, чиї елементи є залишковими класами mod,$p$ то$f(x) \equiv 0$ (mod$p$) має максимум$p$ рішень. Далі якщо$r$ це корінь$x − r$, то є фактором. З іншого боку, неправда, що$f(x) \equiv 0$ (мод$p$) має принаймні один корінь.

Оскільки$x^p − x \equiv 0$ має найбільше$p$ коренів, ми маємо факторизацію.

$x^p - x \equiv x(x - 1)(x - 2) \cdot\cdot\cdot (x - p + 1)$(мод$p$)

Порівняння коефіцієнтів$x$ ми маємо$(p - 1)! \equiv -1$ (мод$p$), що є теоремою Вільсона.

Кейлі дала геометричне доказ теореми Вільсона наступним чином. Розглянемо кількість спрямованих p-кутників з вершинами правильного p-кутника. (Див. Малюнок 3.)

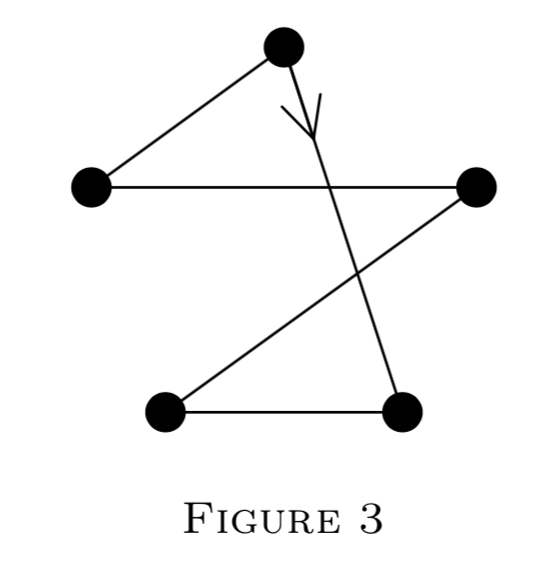
$2019-11-15 12.20.48.png$

Є$(p - 1)!$ в кількості яких$p - 1$ регулярні. Отже, нерегулярні є$(p - 1)! - (p - 1)$ в кількості, і вони приходять у набори обертань.$p$ Звідси

$(p - 1)! - (p - 1) \equiv 0$(мод$p$)

$(p - 1)! + 1 \equiv 0$(мод$p$)

випливає.

Можна також дати геометричний доказ, який одночасно дає обидва

Теореми Ферма і Вільсона ми пропонуємо в якості завдання знайти такий доказ.

Теорема Вільсона дає необхідну і достатню умову для первинності:$p$ є простим тоді і тільки тоді$(p − 1)! \equiv −1$, але навряд чи це практичний критерій.

Конгруенції з заданими коренями

Нехай$a_1$,$a_2$,...,$a_k$ бути набором різних класів залишку (мод$n$). Якщо існує многочлен з цілочисельними коефіцієнтами, такими, що$f(x) \equiv 0$ (мод$m$) має коріння$a_1$,$a_2$,...,$a_k$ і немає інших, ми називаємо цей набір сумісним (мод$n$). Нехай кількість сумісних наборів (мод$n$) позначається символом$C(n)$. Оскільки кількість підмножин множини, що складається з 0, 1, 2,...$2^n$,$n - 1$ є, ми називаємо$c(n) = \dfrac{C(n)}{2^n}$ коефіцієнт сумісності$n$.

Якщо$n = p$ є простим, то конгруентність

$(x - a_1) (x - a_2) \cdot\cdot\cdot (x - a_k) \equiv 0$(мод$n$)

має саме коріння$a_1, a_2, ..., a_n$. Звідси$c(p) = 1$. У недавній роботі М.М. Chokjnsacka Пнєшвака показав, що в$c(4) = 1$ той час як$c(n) < 1$ для$n = 6, 8, 9, 10$. Доведемо це$c(n) < 1$ для кожного композиту$n \ne 4$. Також можна довести, що середнє значення$c(n)$ дорівнює нулю, т. Е.

$\text{lim}_{n \to \infty} \dfrac{1}{n} (c(1) + c(2) + \cdot\cdot\cdot c(n)) = 0$

Так як$c(n) = 1$ для$n = 1$ і$n = p$ ми розглядаємо тільки той випадок, коли$n$ є складовим. Припустимо, що унікальна проста факторизація$n$ задається за$p_{1}^{\alpha_1} p_{2}^{\alpha_2} \cdot\cdot\cdot$ допомогою

$p_{1}^{\alpha_1} > p_{2}^{\alpha_2} > \cdot\cdot\cdot$

Розглянемо окремо випадки

(1)$n$ має більше одного простого дільника, і

(2)$n = p^{\alpha}, \alpha > 1$.

У випадку (1) ми можемо написати

$n = a \cdot b$,$(a, b) = 1, a > b > 1.$

Зараз ми покажемо, що якщо$f(a) \equiv f(b) \equiv 0$ тоді$f(0) \equiv 0$.

Доказ. Нехай$f(x) = c_0 + c_1 + \cdot\cdot\cdot + c_m x^m$. Тоді

$0 \equiv af(b) \equiv ac_0$(мод$n$) і

$0 \equiv bf(a) \equiv bc_0$(мод$n$).

Тепер так як$(a, b) = 1$ існують$r$$s$, такі, що$ar + bs = 1$ так$c_0 (ar + bs) \equiv 0$ і$c_0 \equiv 0$.

У випадку (2) ми можемо написати

$n = p^{\alpha - 1} p.$

Ми показуємо, що$f(p^{\alpha - 1}) \equiv 0$ і маємо$f(0) \equiv 0$ на увазі$f(kp^{\alpha - 1} \equiv 0$,$k = 2, 3, ... .$

Доказ. З тих пір$f(0) \equiv 0$, як у нас$c_0 \equiv 0$,

$f(x) \equiv c_1 + c_2 x^2 + \cdot\cdot\cdot + c_m x^m$, і

$f(p^{\alpha - 1}) \equiv c_1 p^{\alpha - 1} \equiv 0$(мод$p^{\alpha}$),

так що$c_1 \equiv 0$ (мод$p$). Але тепер$f(kp^{\alpha - 1} \equiv 0$, як потрібно.

Про відносно прості послідовності, утворені взаємодіючими поліномами (Ламбек і Мозер)

Нещодавно Беллман поставив наступну проблему. Якщо$p(x)$ є незведеним многочленом з цілими коефіцієнтами і$p(x) > x$ for$x > c$, доведіть, що {$p^n (c)$} не може бути простим для всіх великих$n$. Ми не пропонуємо вирішувати цю проблему, але хочемо зробити деякі зауваження.

Якщо$p(x)$ многочлен з цілими коефіцієнтами, то так і$k^{\text{th}}$ ітерація визначається рекурсивно$p^0 (x) = x$,$p^{p + 1} (x) = p(p^k (x))$. Якщо$a$ і$b$ є цілими числами, то

\[p^k (a) \equiv p^k (b)\ \ \ \ (\text{mod }(a - b))\]

Зокрема для$a = p^n (c)$ і у$b = 0$ нас є$p^{k + n} (c) \equiv p^k (0)$ (мод$p^n(c)$).

Звідси

\[(p^{k + n} (c), p^n (c)) = (p^k(0), p^n(c)).\]

Ми будемо називати послідовність {$a_n$}$n \ge 0$, відносно просту якщо$(a_m, a_n) = 1$ для всіх значень$m, n$, з$m \ne n$. З 5.2 отримуємо

Теорема 1

{$p^n (c)$}$n \ge 0$, є відносно простим, якщо і тільки якщо$(p^k(0), p^n(c)) = 1$ для всіх$k \ge 0$,$n \ge 0$

З випливає відразу результат Беллмана: Якщо$p^k(0) = p(0) \ne 1$ для$k \ge 1$ і якщо$(a, p(0)) = 1$ має на увазі,$(p(a), p(0)) = 1$ то {$p^n(a)$},$n \ge a$ є відносно простим, коли$(c, p(0)) = 1$.

Тепер ми побудуємо всі многочлени,$p(x)$ для яких {$p^n(c)$}$n \ge 0$, є відносно простими для всіх$c$. Згідно теоремі 1,${p^k(0)} = \pm 1$ для всіх$k \ge 1$, як би легко побачити, взявши$n = k$ і$c = 0$. Але тоді {$p^k(0)$} має бути однією з наступних шести послідовностей:

1, 1, 1,...

1, -1, 1,...

1, -1, -1,...

-1, 1, 1,...

-1, 1, -1,...

-1, -1, 1,...

легко помітити, що загальне рішення$p(x)$ (з цілими коефіцієнтами)$m$ рівнянь

$p(a_k) = a_{k +1}$,$k = 0, 1, 2, ..., m - 1.$

виходить з конкретного розчину$p_1 (x)$ наступним чином.

\[p(x) = p_1 (x) + (x - a_1) (x - a_2) \cdot\cdot\cdot (x - a_{k - 1}) \cdot Q(x),\]\

де$Q(x)$ - будь-який многочлен з цілими коефіцієнтами.

Теорема 2

{$p^n (c)$}$n \ge 0$, є відносно простим для всіх,$c$ якщо і тільки якщо$p(x)$ належить до одного з наступних шести класів поліномів.

$1 + x (x - 1) \cdot Q(x)$

$1 - x - x^2 + x(x^2 - 1) \cdot Q(x)$

$1 - 2x^2 + x(x^2 - 1) \cdot Q(x)$

$2x^2 - 1 + x(x^2 - 1) \cdot Q(x)$

$x^2 - x - 1 + x(x^2 - 1) \cdot Q(x)$

$-1 + x(x + 1) \cdot Q(x)$

Доказ: З огляду на (5.3) нам потрібно лише перевірити, чи конкретні рішення дають шість послідовностей, наведених вище.

Про розподіл квадратичних залишків

Великий сегмент теорії чисел можна охарактеризувати, вважаючи його вивченням першої цифри праворуч від цілих чисел. Таким чином, число ділиться на,$n$ якщо його перша цифра дорівнює нулю, коли число виражається базою$n$. Два числа є конгруентними (мод$n$), якщо їх перші цифри однакові в базі$n$. Теорія квадратичних залишків стосується перших цифр квадратів. Особливий інтерес представляє випадок, коли база є праймом, і обмежимося цим випадком.

Якщо взяти, наприклад$p = 7$, то з конгруенціями (мод 7) ми маємо$1^2 \equiv 1 \equiv 6^2$$2^2 \equiv 4 \equiv 5^2$, і$3^2 \equiv 2 \equiv 4^2$; очевидно,$0^2 \equiv 0$. Таким чином, 1, 2, 4 - квадрати, а 3, 5, 6 - неквадрати або незалишки. Якщо$a$ залишок$p$ ми пишемо

$(\dfrac{a}{p}) = + 1$

в той час як якщо$a$ це не залишок ми пишемо

$(\dfrac{a}{p}) = - 1$

Бо$p\ |\ c$ ми пишемо$(\dfrac{c}{p}) = 0$. Цим позначенням зобов'язаний Лежандр. Для$p = 7$ послідовності$(\dfrac{a}{p})$ таким чином

+ - + - -.

$p = 23$Бо виявляється

+ + + - + - + - + - + - + - + - + - - - -.

Ситуація з'ясовується, якщо знову прийняти групову теоретичну точку зору. Класи залишку (мод$p$) утворюють поле, мультиплікативна група якого (містить$p − 1$ елементи) циклічна. Якщо$g$ є генератором цієї групи, то елементи можуть бути записані$g^1, g^2, ..., g^{p−1} = 1$. $g$Парні сили - це квадратичні залишки; вони утворюють підгрупу індексу два. Непарні повноваження$g$ - квадратичні незалишки. З цієї точки зору зрозуміло

$\times$res res = res,$\times$ res норес = норес, норес$\times$ норес = res.

Далі 1/$a$ являє собою унікальний зворотний$a$ (мод$p$) і буде залишком або без залишку відповідно до того, як сам по собі є залишком або без залишку.

Центральною теоремою в теорії квадратичних залишків і дійсно одним з найбільш центральних результатів теорії чисел є Закон квадратичної взаємності, вперше доведений Гауссом близько 1800 року. У ньому зазначено, що

Це призводить до алгоритму прийняття рішення про значення$(\dfrac{p}{q})$.

Надано понад 50 доказів цього закону, включаючи нещодавні докази Зассен-Хауса та Лемера. У першому доказі Гауса (він дав сім) він використав наступну лему, яку він каже нам, що зміг довести лише зі значними труднощами. Для$p = 1$ (мод 4) найменший залишок$p$ не перевищує$2\sqrt{p}+1$. Результати, які ми хочемо сьогодні обговорити, частково покращують цей результат і загалом стосуються розподілу послідовності + та − in$(\dfrac{a}{p})$,$a = 1, 2, ..., p − 1$.

У 1839 році Діріхле, як побічний продукт свого дослідження класового числа квадратичних форм, встановив наступну теорему: Якщо$p \equiv 3$ (мод 4) то серед цілих чисел залишається більше залишків$1, 2, ..., \dfrac{p−1}{2}$, ніж незалишків. Хоча це елементарне твердження про цілі числа, всі опубліковані докази, включаючи останні, дані Чунгом, Чоулою, Вітменом, Карліцем та Мозером, включають ряди Фур'є. Ландау був дуже прагнув мати елементарний доказ. Хоча Вітмен і Карліц дали дещо пов'язані результати, результат Діріхле досить ізольований. Таким чином, жоден подібний нетривіальний результат не відомий для інших діапазонів.

У 1896 році Аладов, у 1898 р. фон Стернек, а в 1906 році Якобстхол зайнялися питанням про те, скільки разів з'являються комбінації ++, +−, −+ та −−. Вони показали, що кожна з чотирьох можливостей з'явилася, як можна було очікувати, з частотою 1/4. У 1951 році Перрон знову вивчив питання і довів, що подібні результати тримають, якщо замість послідовних цілих чисел один розглядає цілі числа, розділені на відстань$d$. J.B. Kelly нещодавно довів результат, який, грубо кажучи, показує, що залишки і незалишки характеризуються цією властивістю. Jacobsthall також отримав часткові результати для випадків 3 послідовних залишків та незалишків. $R_n$$N_n$Дозволяти і бути кількість блоків$n$ послідовних залишків і не залишків відповідно. Можна здогадатися, що$R_n \thicksim N_n \thicksim \dfrac{p}{2^n}$. Серед тих, хто сприяв цьому питанню, - Вандівер, Беннет, Дорж, Хопф, Девенпорт, А. Брауер. Мабуть, найцікавішим результатом є той, що у А.Брауера. Він показав, що для$p > p_0 (n)$,$R_n > 0$ і$N_n > 0$. Намалюємо частину його доказу. Це залежить від дуже цікавого результату Ван дер Ваердена (1927). Враховуючи$k$$\ell$, існує$N = N(k, \ell)$ таке ціле число, що якщо розділити цілі числа$1, 2, ..., N$ на$k$ класи будь-яким чином, принаймні один з класів буде містити арифметичну прогресію довжини l. теорема, до якої ми повернемося в наступному розділі.

Повертаючись до роботи Брауера, покажемо, що він доводить, що всі великі прайми мають, скажімо, 7 послідовних залишків. Один розділяє числа$1, 2, ..., p − 1$ на 2 класи, залишки та незалишки. Якщо$p$ він досить великий, один з цих класів буде містити, за теоремою Ван дер Вердена, 49 членів в арифметичній прогресії, скажімо

$a, a + b, a + 2b, ..., a + 48b.$

Тепер, якщо$\dfrac{a}{b} = c$ тоді у нас є 49 послідовних чисел того ж квадратичного символу, а саме

$c, c + 1, c + 2, ..., c + 48.$

і результат завершений.

Доказ існування незалишків значно складніше. Крім того, цікаво зауважити, що існування блоків s на кшталт + − + − не$\cdot\cdot\cdot$ охоплюється цими методами.

Тепер повернемося до питання, поставленого Гауссом. Що можна сказати про найменший$n_p$ незалишок простого? Оскільки 1 - це залишок, відповідне питання про залишки - «що таке найменший основний$r_p$ залишок$p$?». Ці питання були атаковані в 1920-х роках низкою математиків, включаючи Нагель, Шур, Поля, Цайц, Ландау, Вандівер, Брауер, і Виноградов. Нагель, наприклад, довів, що для$p \ne 7$, 23,$n_p < \sqrt{p}$. Поля і Щур довели, що

$\sum_{n = a}^{b} (\dfrac{n}{p}) < \sqrt{p} \log p.$

Це означає, що ніколи не існує більше, ніж$\sqrt{p} \log p$ послідовних залишків або залишків, і це коливається набагато більше, ніж$\sqrt{p} \log p$ має приблизно стільки ж залишків, скільки незалишків. Використовуючи цей результат і деякі теореми про розподіл простих чисел, Виноградов довів$p > p_0$, що для

$n_p < p^{\dfrac{1}{2\sqrt{e}}} \log ^2 p < n^{.303}.$

Перевіряючи доказ Виноградова, ми виявили, що за його методом$p_0$ надмірно великий, скажімо$p_0 > 10^{10^{10}}$. Проте, незважаючи на численні спроби, цей результат Виноградова не сильно покращився.

У 1938 р.$\ddot{o}$ Ерд с і Ко показали, що існування малих незалишків тісно пов'язане з неіснуванням евклідового алгоритму в квадратичних полах. Це призвело Brauer, Hua, Min до перегляду питання про явні межі для найменшого залишку. Брауер вже в 1928 році довів ряд таких результатів, характерним для яких є те, що для всіх$p \equiv 1$ (mod 8),

$n_p < (2p)^{.4} + 3 (2p)^{.2} + 1$

і Хуа і Мін довели, наприклад, що для$p > e^{250}$,

$n_p < (60 \sqrt{p})^{.625}$.

Невеликі прості числа (до 10 000 000) розглядали Беннет, Чатланд, Брауер, Мозер та ін.

Зовсім недавно до цих проблем застосовували недоведену розширену гіпотезу Рімана Ліннік, Чоула,$\ddot{o}$ Ерд з та Енкені. Так, наприклад, Енкені використовувала розширену гіпотезу Рімана, щоб довести це$n_p \ne O(\log ^2 p)$. У зворотному напрямку Піллай (1945) це довів$p \ne o(\log \log p)$. Використовуючи спочатку гіпотезу Рімана, а пізніше деякі глибокі результати Лінніка на прості числа в арифметичній прогресії, Фрідлендер і Чоула покращили це до$n_p \ne o(\log p)$.

Зовсім недавно був ряд результатів в дещо іншому напрямку Brauer, Nagel, Skolem, Redei і Kanold. Метод Redei особливо цікавий. Він використовує скінченний проективний геометричний аналог фундаментальної теореми Мінковського на вогнутих тілах, щоб довести, що для$p \equiv 1$ (mod 4) принаймні$\dfrac{1}{7}$ з чисел до$\sqrt{p}$ є залишками і щонайменше 1 є незалишками. Наші власні недавні внески в теорію полягають у цих напрямках. Ми окреслимо деякі з цієї роботи.

Розглянемо спочатку решітку точок в квадраті сторони$m$. Шукаємо оцінку$V(m)$, кількість видимих точок решітки в квадраті. Як і на попередньому пункті знаходимо

$[m]^2 = V(m) + V(\dfrac{m}{2}) + \cdot\cdot\cdot$

і інвертування за формулою інверсії Mobius дає

$V(m) = \sum_{d \ge 1} \mu (d) [\dfrac{m}{d}]^2$.

Як і раніше, це призводить до асимптотичної оцінки.

$V(m) \thicksim \dfrac{6}{\pi^2} m^2.$

Однак ми можемо отримати чіткі оцінки для$v(m)$ також. Дійсно, з точної формули$V(m)$ вище можна показати, що для всіх$m$,$V (m) > .6m^2$. Ми зараз беремо$m = [\sqrt{p}]$. Для розумно великих$p$ ми матимемо$V([\sqrt{p}]) > .59m^2$. Тепер з кожною видимою точкою решітки$(a, b)$ пов'язуємо число$\dfrac{a}{b}$ (мод$p$). Тепер ми покажемо, що різні видимі точки відповідають різним числам. Таким чином, якщо$\dfrac{a}{b} = \dfrac{c}{d}$ тоді$ad \equiv bc$. Але$ad < p$ і$bc < p$. Звідси$ad = bc$ і$\dfrac{a}{b} = \dfrac{c}{d}$. Проте$(a, b) = (c, d) = 1$ так, що$a = c$ і$b = d$.

Оскільки ми маємо щонайменше .59 різних чисел$\dfrac{a}{b}$, представлених дробами$a < \sqrt{p}$$b < \sqrt{p}$, принаймні .09 з них буде відповідати незалишкам. Якщо$R$ позначає кількість залишків$< \sqrt{p}$ і$N$ кількість незалишків$< \sqrt{p}$, то$R + N = \sqrt{p}$ і$2RN > .09p$. Рішення цих нерівностей дає$R, N > .04 \sqrt{p}$. Це слабкіше, ніж результат Нагеля, але має перевагу утримування простих чисел$p \equiv 3$ (мод 4), а також$p \equiv 1$ (мод 4). Таким чином, винятки виходять тільки прості числа 7 і 23. Для простих чисел$p \equiv 1$ (mod 4) −1 є незалишком, і це може бути використано разом з вищевказаним методом для отримання більш сильних результатів. Можна також використовувати існування багатьох незалишків <,$\sqrt{p}$ щоб довести існування одного невеликого залишку, але результати, отримані таким чином, не такі сильні, як результат Виноградова.