1.E: Функції (вправи)

1.1: Функції та позначення функцій

Реактивний лайнер змінює висоту, оскільки його відстань від початкової точки польоту збільшується. Вага зростаючої дитини з часом збільшується. У кожному конкретному випадку одна кількість залежить від іншого. Існує взаємозв'язок між двома величинами, які ми можемо описати, аналізувати та використовувати для прогнозування. У цьому розділі ми розберемо такі відносини.

Вербальний

1) У чому різниця між відношенням і функцією?

Відповідь

Відношення - це набір впорядкованих пар. Функція - це особливий вид відношення, в якому жодна дві впорядковані пари не мають однакової першої координати.

2) У чому різниця між входом і виходом функції?

3) Чому тест вертикальної лінії говорить нам, чи є графік відношення функцію?

Відповідь

Коли вертикальна лінія перетинає графік відношення більше одного разу, це вказує на те, що для цього входу є більше одного виводу. У будь-якому конкретному вхідному значенні може бути лише один вихід, якщо відношення має бути функцією.

4) Як можна визначити, чи є відношення функцією один до одного?

5) Чому тест горизонтальної лінії говорить нам, чи є графік функції один до одного?

Відповідь

Коли горизонтальна лінія перетинає графік функції більше одного разу, це вказує на те, що для цього виводу є кілька вхідних даних. Функція є один до одного, якщо кожен вихід відповідає лише одному входу.

алгебраїчна

Для вправ 6-7 визначте, чи представляє відношення функцію.

6)\(\{(a,b), (c,d), (a,c)\}\)

7)\(\{(a,b),(b,c),(c,c)\}\)

Відповідь

функція

Для вправ 8-26 визначте, чи представляє відношення\(y\) як функцію\(x\).

8)\(5x+2y=10\)

9)\(y=x^2\)

Відповідь

функція

10)\(x=y^2\)

11)\(3x^2+y=14\)

Відповідь

функція

12)\(2x+y^2=6\)

13)\(y=−2x^2+40x\)

Відповідь

функція

14)\(y=\dfrac{1}{x}\)

15)\(x=\dfrac{3y+5}{7y−1}\)

Відповідь

функція

16)\(x=\sqrt{1−y^2}\)

17)\(y=\dfrac{3x+5}{7x−1}\)

Відповідь

функція

18)\(x^2+y^2=9\)

19)\(2xy=1\)

Відповідь

функція

20)\(x=y^3\)

21)\(y=x^3\)

Відповідь

функція

22)\(y=\sqrt{1−x^2}\)

23)\(x=\pm\sqrt{1-y}\)

Відповідь

функція

24)\(y=\pm\sqrt{1−x}\)

25)\(y^2=x^2\)

Відповідь

не є функцією

26)\(y^3=x^2\)

Для вправ 27-39 оцініть функцію\(f\) за вказаними значеннями\(f(−3),f(2),f(−a),−f(a),f(a+h)\).

27)\(f(x)=2x−5\)

Відповідь

\(f(−3)=−11\);\(f(2)=−1\)\(f(−a)=−2a−5\);\(−f(a)=−2a+5\);\(f(a+h)=2a+2h−5\)

28)\(f(x)=−5x^2+2x−1\)

29)\(f(x)=\sqrt{2−x}+5\)

Відповідь

\(f(−3)=\sqrt{5+5}\);\(f(2)=5\)\(f(−a)=\sqrt{2+a+5}\);\(−f(a)=−\sqrt{2−a}−5\);\(f(a+h)=\sqrt{2−a−h}+5\)

30)\(f(x)=\dfrac{6x−1}{5x+2}\)

31)\(f(x)=|x−1|−|x+1|\)

Відповідь

\(f(−3)=2\);\(f(2)=1−3=−2\)\(f(−a)=|−a−1|−|−a+1|\);\(−f(a)=−|a−1| +|a+1|\);\(f(a+h)= |a+h−1|−|a+h+1|\)

32) З огляду на функцію\(g(x)=5−x^2\), оцінювати\(g(x+h)−g(x)h\),\(h{\neq}0\).

33) З огляду на функцію\(g(x)=x^2+2x\), оцінювати\(\dfrac{g(x)−g(a)}{x−a}\),\(x{\neq}a\).

Відповідь

\(\dfrac{g(x)−g(a)}{x−a}=x+a+2\),\(x{\neq}a\)

34) Задано функцію\(k(t)=2t−1\):

а. оцінювати\(k(2)\).
б. вирішувати\(k(t)=7\).

35) З огляду на функцію\(f(x)=8−3x\):

а. оцінювати\(f(−2)\).
б. вирішувати\(f(x)=−1\).

Відповідь

а.\(f(−2)=14\); б.\(x=3\)

36) З огляду на функцію\(p(c)=c^2+c\):

а. оцінювати\(p(−3)\).
б. вирішувати\(p(c)=2\).

37) З огляду на функцію\(f(x)=x^2−3x\):

а. оцінювати\(f(5)\).
б. вирішувати\(f(x)=4\).

Відповідь

а.\(f(5)=10\); б.\(x=−1\) або\(x=4\)

38) З огляду на функцію\(f(x)=\sqrt{x+2}\):

а. оцінювати\(f(7)\).
б. вирішувати\(f(x)=4\).

39) Розглянемо відносини\(3r+2t=18\).

а) Напишіть зв'язок як функцію\(r=f(t)\).
б Оцінити\(f(−3)\).
c. вирішувати\(f(t)=2\).

Відповідь

а.\(f(t)=6−\frac{2}{3}t\); б.\(f(−3)=8\); в.\(t=6\)

Графічний

Для вправ 40-54 використовуйте тест вертикальної лінії, щоб визначити, які графіки показують відносини, які є функціями.

40)

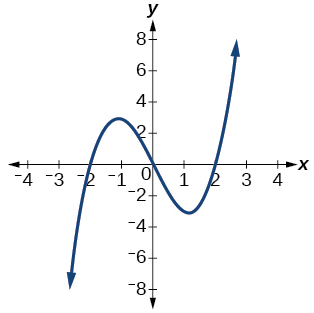
41)

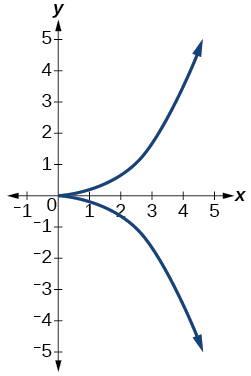
Відповідь

не є функцією

42)

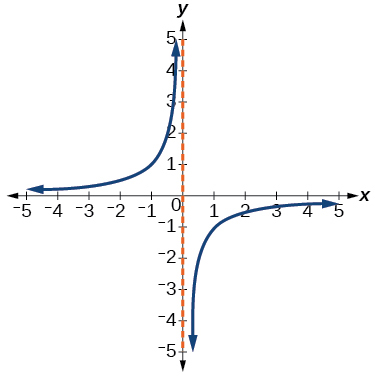
43)

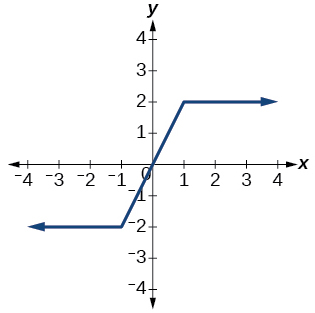
Відповідь

функція

44)

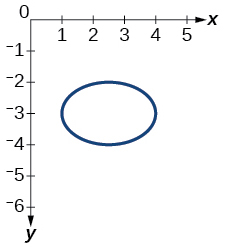
45)

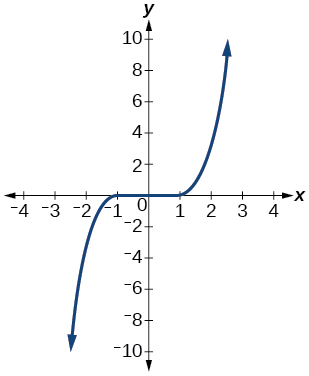
Відповідь

функція

46)

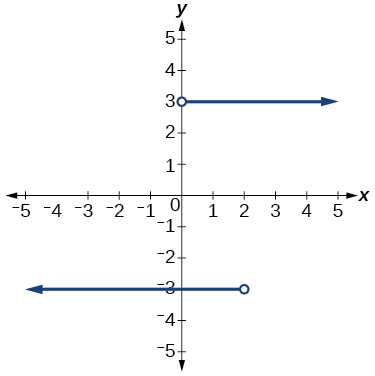
47)

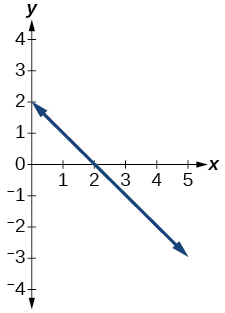
Відповідь

функція

48)

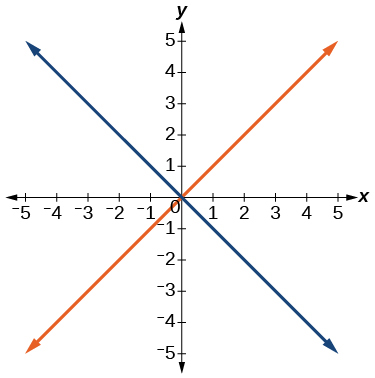
49)

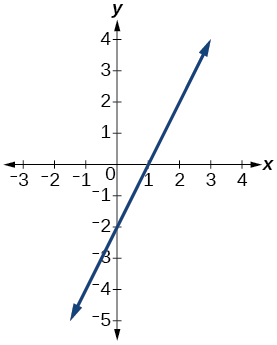
Відповідь

функція

50)

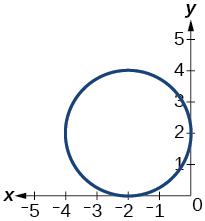
51)

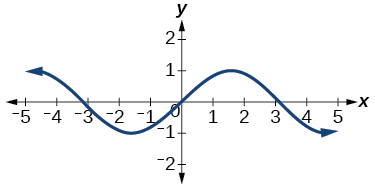
Відповідь

функція

52) З огляду на наступний графік,

• Оцінити\(f(−1)\).
• Вирішити для\(f(x)=3\).

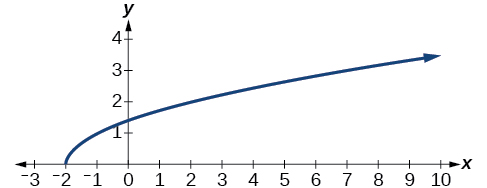
53) З огляду на наступний графік,

• Оцінити\(f(0)\).
• Вирішити для\(f(x)=−3\).

Відповідь

а.\(f(0)=1\); б.\(f(x)=−3\),\(x=−2\) або\(x=2\)

54) З огляду на наступний графік,

• Оцінити\(f(4)\).
• Вирішити для\(f(x)=1\).

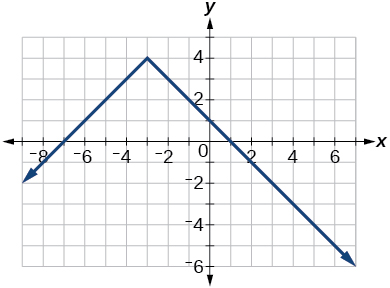
Для вправ 55-59 визначте, чи є даний графік функцією один до одного.

55)

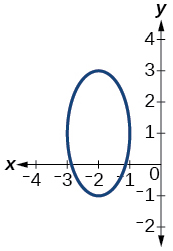
Відповідь

не є функцією, тому це також не функція один-на-один

56)

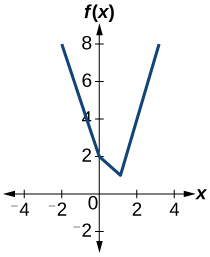
57)

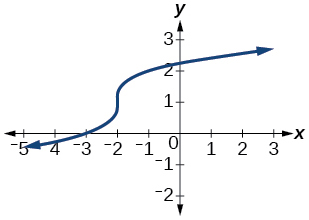
Відповідь

функція «один-на-один»

58)

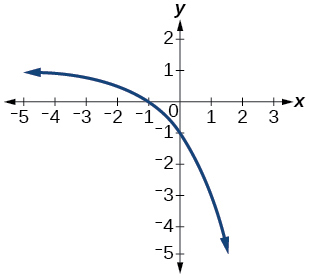
59)

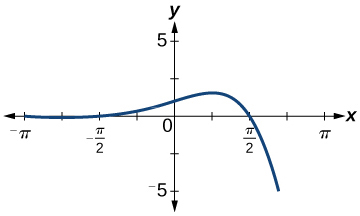
Відповідь

функція, але не один-на-один

Числові

Для вправ 60-62 визначте, чи представляє відношення функцію.

60)\(\{(−1,−1),(−2,−2),(−3,−3)\}\)

61)\(\{(3,4),(4,5),(5,6)\}\)

Відповідь

функція

62)\((2,5),(7,11),(15,8),(7,9)\}\)

Для вправ 63-65 визначте, чи відповідає відношення, представлене в табличній формі,\(y\) як функцію\(x\).

63)

\(x\)	5	10	15
\(y\)	3	8	14

Відповідь

функція

64)

\(x\)	5	10	15
\(y\)	3	8	8

65)

\(x\)	5	10	10
\(y\)	3	8	14

Відповідь

не є функцією

Для вправ 66-67 використовуйте функцію,\(f\) представлену в таблиці нижче

\(x\)	\(f(x)\)
\ (x\) ">0	\ (f (x)\) ">74
\ (x\) ">1	\ (f (x)\) ">28
\ (x\) ">2	\ (f (x)\) ">1
\ (x\) ">3	\ (f (x)\) ">53
\ (x\) ">4	\ (f (x)\) ">56
\ (x\) ">5	\ (f (x)\) ">3
\ (x\) ">6	\ (f (x)\) ">36
\ (x\) ">7	\ (f (x)\) ">45
\ (x\) ">8	\ (f (x)\) ">14
\ (x\) ">9	\ (f (x)\) ">47

66) Оцініть\(f(3)\).

67) Вирішити\(f(x)=1\).

Відповідь

\(f(x)=1\),\(x=2\)

Для вправ 68-73 оцініть функцію\(f\) за значеннями\(f(−2)\),\(f(−1)\),\(f(0)\),\(f(1)\), і\(f(2)\).

68)\(f(x)=4−2x\)

69)\(f(x)=8−3x\)

Відповідь

\(f(−2)=14\);\(f(−1)=11\)\(f(0)=8\);\(f(1)=5\);\(f(2)=2\)

70)\(f(x)=8x^2−7x+3\)

71)\(f(x)=3+\sqrt{x+3}\)

Відповідь

\(f(−2)=4\);\(f(−1)=4.414\)\(f(0)=4.732\);\(f(1)=4.5\);\(f(2)=5.236\)

72)\(f(x)=\dfrac{x-2}{x+3}\)

73)\(f(x)=3^x\)

Відповідь

\(f(−2)=\frac{1}{9}\);\(f(−1)=\frac{1}{3}\)\(f(0)=1\);\(f(1)=3\);\(f(2)=9\)

Для вправ 74-75 оцініть вирази, задані функції\(f\)\(g\), і\(h\):

• \(f(x)=3x−2\)
• \(g(x)=5−x^2\)
• \(h(x)=−2x^2+3x−1\)

74)\(3f(1)−4g(−2)\)

75)\(f \left (\dfrac{7}{3} \right )−h(−2)\)

Відповідь

\(20\)

Технологія

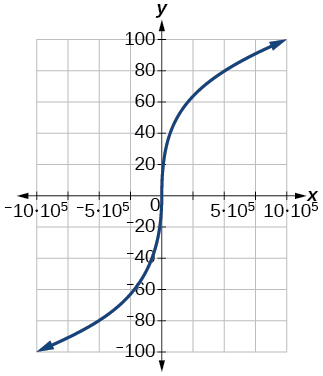
Для вправ 76-78, графік\(y=x^2\) на даному оглядовому вікні. Визначте відповідний діапазон для кожного оглядового вікна. Показувати кожен графік.

76)\([−0.1, 0.1]\)

77)\([−10, 10]\)

Відповідь

\([0, 100]\)

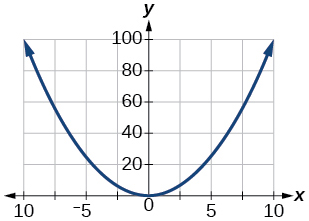
78)\([−100,100]\)

Для вправ 79-81 графік\(y=x^3\) на даному оглядовому вікні. Визначте відповідний діапазон для кожного оглядового вікна. Показувати кожен графік.

79)\([−0.1, 0.1]\)

Відповідь

\([−0.001, 0.001]\)

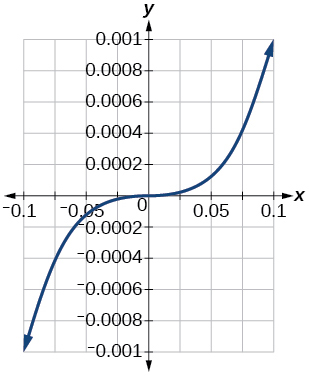
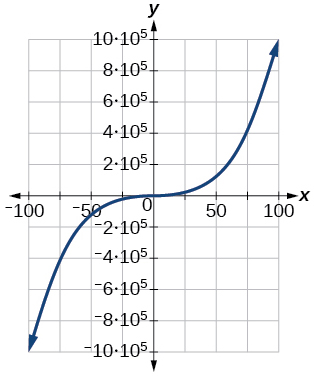
80)\([−10, 10]\)

81)\([−100, 100]\)

Відповідь

\([−1,000,000, 1,000,000]\)

Для вправ 82-84 графік\(y=\sqrt{x}\) на даному оглядовому вікні. Визначте відповідний діапазон для кожного оглядового вікна. Показувати кожен графік.

82)\([0, 0.01]\)

83)\([0, 100]\)

Відповідь

\([0, 10]\)

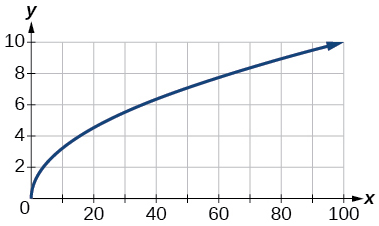
84)\([0, 10,000]\)

Для вправ 85-87, графік\(y=\sqrt[3]{x}\) на даному оглядовому вікні. Визначте відповідний діапазон для кожного оглядового вікна. Показувати кожен графік.

85)\([−0.001,0.001]\)

Відповідь

\([−0.1,0.1]\)

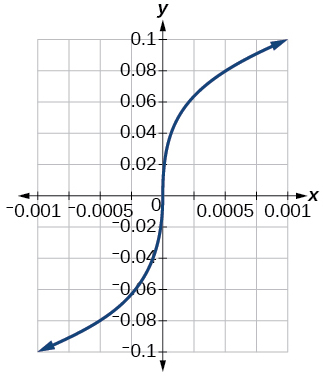
86)\([−1000,1000]\)

87)\([−1,000,000,1,000,000]\)

Відповідь

\([−100, 100]\)

Реальні програми

88) Кількість сміття\(G\), виробленого містом з населенням,\(p\) дається по\(G=f(p)\). \(G\)вимірюється в тонни на тиждень, і\(p\) вимірюється тисячами людей.

Місто Тола має населення\(40,000\) і виробляє\(13\) тонни сміття щотижня. Висловлюйте цю інформацію з точки зору функції\(f\) .Тола має населення\(40,000\) і виробляє\(13\) тонни сміття щотижня. Висловіть цю інформацію з точки зору функції\(f\).
Поясніть сенс висловлювання\(f(5)=2\).

89) Кількість кубічних ярдів бруду\(D\), необхідних для покриття саду площею квадратних футів задається\(D=g(a)\).

а Сад з площею\(5000\)\(ft^2\) вимагає\(50\)\(yd^3\) бруду. Висловіть цю інформацію з точки зору функції\(g\).
б. пояснити значення висловлювання\(g(100)=1\).

Відповідь

а.\(g(5000)=50\); б. Кількість кубічних ярдів бруду, необхідного для саду\(100\) квадратних футів, становить\(1\).

90) Нехай\(f(t)\) буде кількість качок в озері\(t\) років після 1990 року. Поясніть сенс кожного твердження:

а. ф (5) =30
б. ф (10) =40

91)\(h(t)\) Дозволяти висоті над землею, в футах, ракети\(t\) секунд після запуску. Поясніть сенс кожного твердження:

а.\(h(1)=200\)
б.\(h(2)=350\)

Відповідь

а Висота ракети над землею після\(1\) секунди -\(200\) фут. б. висота ракети над землею через\(2\) секунди становить\(350\) фут.

92) Показати,\(f(x)=3(x−5)^2+7\) що функція не один до одного.

1.2: Домен і діапазон

Створюючи різні функції за допомогою даних, ми можемо ідентифікувати різні незалежні та залежні змінні, а також аналізувати дані та функції для визначення домену та діапазону. У цьому розділі ми розглянемо методи визначення області та діапазону функцій.

Вербальний

1) Чому домен відрізняється для різних функцій?

Відповідь

Область функції залежить від того, які значення незалежної змінної роблять функцію невизначеною або уявною.

2) Як ми визначаємо область функції, визначеної рівнянням?

3) Поясніть, чому домен відрізняється від домену\(f(x)=\sqrt{x}\).\(f(x)=\sqrt[3]{x}\)

Відповідь

Немає обмежень на x,\(f(x)=\sqrt[3]{x}\) оскільки ви можете взяти кубічний корінь будь-якого дійсного числа. Таким чином, домен все реальні числа,\((−∞,∞)\). Маючи справу з безліччю дійсних чисел, ви не можете взяти квадратний корінь від'ємних чисел. Таким чином, значення x обмежені\(f(x)=\sqrt{x}\) для невід'ємних чисел і домен є\([0,∞)\).

4) При описі множин чисел за допомогою інтервальних позначень, коли ви використовуєте дужки і коли використовуєте дужку?

5) Як ви графуєте кускову функцію?

Відповідь

Графік кожної формули кускової функції над відповідною області. Використовуйте однакову шкалу для осі x та осі y для кожного графіка. Вкажіть інклюзивні кінцеві точки суцільним колом і ексклюзивні кінцеві точки з відкритим колом. Використовуйте стрілку для позначення\(−∞\) або\(∞\). Об'єднайте графіки, щоб знайти графік кускової функції.

алгебраїчна

Для вправ 6-25 знайдіть область кожної функції за допомогою інтервальних позначень.

6)\(f(x)=−2x(x−1)(x−2)\)

7)\(f(x)=5−2x^2\)

Відповідь

\((-\infty,\infty)\)

8)\(f(x)=3\sqrt{x-2}\)

9)\(f(x)=3-\sqrt{6-2x}\)

Відповідь

\(\left(-\infty,3\right]\)

10)\(f(x)=\sqrt{4-3x}\)

11)\(f(x)=\sqrt{x^2+4}\)

Відповідь

\((-\infty,\infty)\)

12)\(f(x)=\sqrt[3]{1-2x}\)

13)\(f(x)=\sqrt[3]{x-1}\)

Відповідь

\((-\infty,\infty)\)

14)\(f(x)=\dfrac{9}{x-6}\)

15)\(f(x)=\dfrac{3x+1}{4x+2}\)

Відповідь

\(\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )\)

16)\(f(x)=\dfrac{\sqrt{x+4}}{x-4}\)

17)\(f(x)=\dfrac{x-3}{x^2+9x-22}\)

Відповідь

\((-\infty,-11)\cup(-11,2)\cup(2,\infty)\)

18)\(f(x)=\dfrac{1}{x^2-x-6}\)

19)\(f(x)=\dfrac{2x^3−250}{x^2−2x−15}\)

Відповідь

\((-\infty,-3)\cup(-3,5)\cup(5,\infty)\)

20)\(\dfrac{5}{\sqrt{x-3}}\)

21)\(\dfrac{2x+1}{\sqrt{5-x}}\)

Відповідь

\((-\infty,5)\)

22)\(\dfrac{\sqrt{x-4}}{\sqrt{x-6}}\)

23)\(\dfrac{\sqrt{x-6}}{\sqrt{x-4}}\)

Відповідь

\(\left[6,\infty\right)\)

24)\(f(x)=\dfrac{x}{x}\)

25)\(f(x)=\dfrac{x^2-9x}{x^2-81}\)

Відповідь

\((-\infty,-9)\cup(-9,9)\cup(9,\infty)\)

26) Знайти домен функції за\(f(x)=\sqrt{2x^3-50x}\) допомогою:

a. за допомогою алгебри

b. графічне відображення функції в радиканді та визначення інтервалів на осі x, для яких радиканд є невід'ємним.

Графічний

Для вправ 27-37 запишіть область і діапазон кожної функції за допомогою інтервальних позначень.

27)

\ (\ вліво (2, 8\ вправо]\).» style="фон: прозорий; кордону нижнього кольору: RGB (0, 0, 0); кордону нижнього стилю: немає; кордону знизу ширина: 0px; кордону зображення-початок: 0; межа зображення-повторити: стрейч; кордону зображення-зріз: 100%; кордону зображення-джерело: немає; кордону зображення-ширина: 1; межа зображення-колір: rgb ( 0, 0, 0); кордону лівого стилю: немає; кордону лівої ширини: 0px; кордону правого кольору: RGB (0, 0, 0); кордону правої стиль: немає; кордону правої ширини: 0px; кордону верхнього кольору: RGB (0, 0, 0); кордон верхнього стилю: немає; кордону верхньої ширини: 0px; колір: RGB (0, 0, 0); курсор: за замовчуванням; сімейство шрифтів: лато, ari Al, Helvetica, без зарубок, & quot; Arial Unicode мс»; розмір шрифту: 16px; шрифт стиль: нормальний; шрифт варіант: нормальний; вага шрифту: 400; висота: 200px; інтервал між листами: нормальний; максимальна ширина: 1224px; непрозорість: 0,8; сироти: 2; вирівнювання тексту: центр; текстовий декор: немає; текстовий відступ: 0px; текст-перетворення: немає; -webkit-текст-штрих-ширина: 0px; білий -простір: нормальний; ширина: 200px; інтервал слів: 0px;» ширина = «200px» висота = «200px» src =» https://math.libretexts.org/@api/dek..._01_02_202.jpg "/>

Відповідь

домен:\(\left(2,8\right]\), діапазон\(\left[6,8\right)\)

28)

\ (\ лівий [4, 8\ вправо)\).» style="фон: прозорий; кордону нижнього кольору: RGB (0, 0, 0); кордону нижнього стилю: немає; кордону нижньої ширини: 0px; кордону зображення-початок: 0; межа зображення-повторити: стрейч; кордону зображення-зріз: 100%; кордону зображення-джерело: немає; кордону зображення-ширина: 1; межа зображення-колір: rgb ( 0, 0, 0); кордону лівого стилю: немає; кордону лівої ширини: 0px; кордону правого кольору: RGB (0, 0, 0); кордону правої стиль: немає; кордону правої ширини: 0px; кордону верхнього кольору: RGB (0, 0, 0); кордон верхнього стилю: немає; кордону верхньої ширини: 0px; колір: RGB (0, 0, 0); курсор: за замовчуванням; сімейство шрифтів: лато, ari Al, Helvetica, без зарубок, & quot; Arial Unicode мс»; розмір шрифту: 16px; шрифт стиль: нормальний; шрифт варіант: нормальний; вага шрифту: 400; висота: 200px; інтервал між листами: нормальний; максимальна ширина: 1224px; непрозорість: 0,8; сироти: 2; вирівнювання тексту: центр; текстовий декор: немає; текстовий відступ: 0px; текст-перетворення: немає; -webkit-текст-штрих-ширина: 0px; білий -простір: нормальний; ширина: 200px; інтервал слів: 0px;» ширина = «200px» висота = «200px» src =» https://math.libretexts.org/@api/dek..._01_02_203.jpg "/>

29)

Відповідь

домен:\([−4, 4]\), діапазон:\([0, 2]\)

30)

31)

Відповідь

домен:\(\left[−5, 3\right)\), діапазон:\([0,2]\)

32)

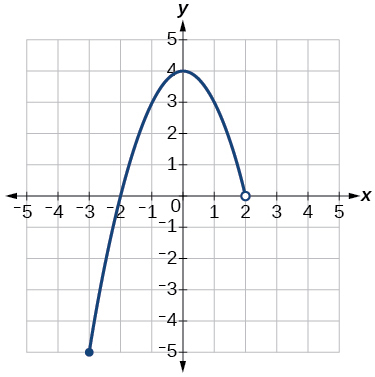
33)

Відповідь

домен:\(\left(−\infty,1\right]\), діапазон:\(\left[0,\infty\right)\)

34)

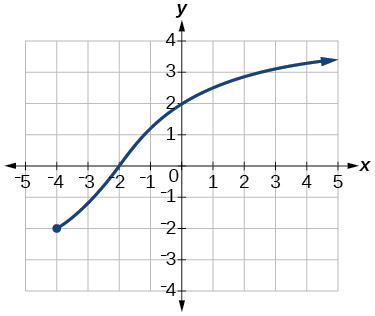
35)

Відповідь

домен:\([−6,−16]\cup[16,6]\); діапазон:\([−6,−16]\cup[16,6]\)

36)

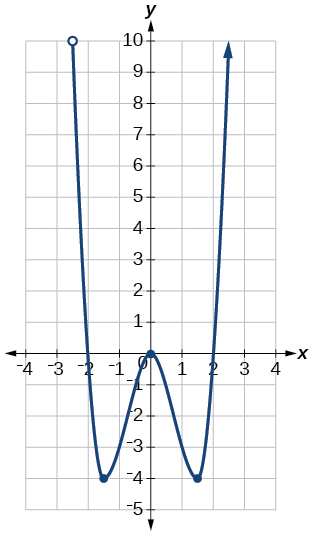
37)

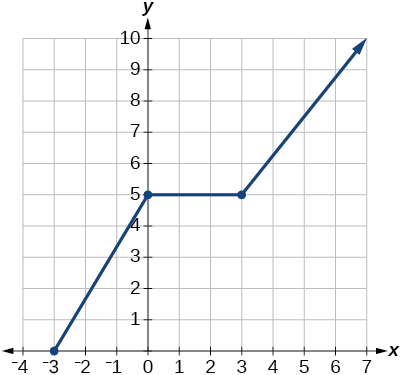
Відповідь

домен:\(\left[−3, \infty\right)\); діапазон:\(\left[0,\infty\right)\)

Для вправ 38-45 накидайте графік кускової функції. Запишіть домен в інтервальне позначення.

38)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

39)\(f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}\)

Відповідь

домен:\((−\infty,\infty)\)

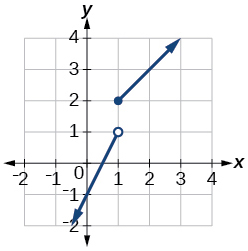
40)\(f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}\)

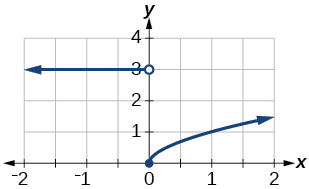
41)\(f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}\)

Відповідь

домен:\((−\infty,\infty)\)

42)\(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}\)

43)\(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}\)

Відповідь

домен:\((−\infty,\infty)\)

44)\(f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}\)

45)\(f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}\)

Відповідь

домен:\((−\infty,\infty)\)

Числові

Для вправ 46-48, з огляду на кожну функцію\(f\), оцінюють\(f(−3)\)\(f(−2)\),,\(f(−1)\), і\(f(0)\).

46)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

47)\(f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}\)

Відповідь

\(f(−3)=1\)\(f(−2)=0\);\(f(−1)=0\);\(f(0)=0\)

48)\(f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}\)

Для вправ 49-51, з огляду на кожну функцію\(f\), оцінюють\(f(−1)\)\(f(0)\),,\(f(2)\), і\(f(4)\).

49)\(f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}\)

Відповідь

\(f(−1)=−4\)\(f(0)=6\);\(f(2)=20\);\(f(4)=34\)

50)\(f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}\)

51)\(f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}\)

Відповідь

\(f(−1)=−5\)\(f(0)=3\);\(f(2)=3\);\(f(4)=16\)

Для вправ 52-54 запишіть домен для кускової функції в інтервальних позначеннях.

52)\(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)

53)\(f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}\)

Відповідь

домен:\((−\infty,1)\cup(1,\infty)\)

54)\(f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}\)

Технологія

55) Графік\(y=\dfrac{1}{x^2}\) на оглядовому вікні\([−0.5,−0.1]\) і\([0.1,0.5]\). Визначте відповідний діапазон для оглядового вікна. Покажіть графіки.

Відповідь

вікно:\([−0.5,−0.1]\); діапазон:\([4, 100]\)

вікно:\([0.1, 0.5]\); діапазон:\([4, 100]\)

56) Графік\(y=\dfrac{1}{x}\) на оглядовому вікні\([−0.5,−0.1]\) і\([0.1, 0.5]\). Визначте відповідний діапазон для оглядового вікна. Покажіть графіки.

Розширення

57) Припустимо, діапазон функції\(f\) є\([−5, 8]\). Що таке асортимент\(|f(x)|\)?

Відповідь

\([0, 8]\)

58) Створіть функцію, в якій діапазон - це все невід'ємні дійсні числа.

59) Створіть функцію, в якій знаходиться домен\(x>2\).

Відповідь

Багато відповідей. Однією з функцій є\(f(x)=\dfrac{1}{\sqrt{x-2}}\).

Реальні програми

60) Висота\(h\) снаряда - це функція часу, коли\(t\) він знаходиться в повітрі. Висота в ногах за\(t\) секунди задається функцією\(h(t)=−16t^2+96t\). Що таке область функції? Що означає домен в контексті проблеми?

Відповідь

Домен є\([0, 6]\); це займає 6 секунд, щоб снаряд покинув землю і повернувся на землю

61) Вартість в доларах виготовлення\(x\) предметів задається функцією\(C(x)=10x+500\).

а Фіксована вартість визначається, коли виробляються нульові позиції. Знайдіть фіксовану вартість за цією статтею.

б Яка вартість виготовлення\(25\) предметів?

c Припустимо, що максимальна вартість дозволена є\(\$1500\). Що таке домен і діапазон функції витрат\(C(x)\)?

1.3: Швидкість зміни та поведінка графіків

У цьому розділі ми розберемо зміни у функціях. Наприклад, швидкість зміни пов'язує зміну вихідної кількості зі зміною вхідної кількості. Середня швидкість зміни визначається з використанням тільки початкових і кінцевих даних. Визначення точок, які позначають інтервал на графіку, можна використовувати для пошуку середньої швидкості зміни. Порівняння пар вхідних і вихідних значень у таблиці також може бути використано для пошуку середньої швидкості зміни.

Вербальний

1) Чи може середня швидкість зміни функції бути постійною?

Відповідь

Так, середня швидкість зміни всіх лінійних функцій постійна.

2) Якщо функція\(f\) збільшується на\((a,b)\) і зменшується далі\((b,c)\), то що можна сказати про локальному екстремумі\(f\) on\((a,c)\)?

3) Чим абсолютний максимум і мінімум схожі і відрізняються від локальної крайності?

Відповідь

Абсолютний максимум і мінімум відносяться до всього графіку, тоді як локальні екстремуми відносяться тільки до певної області навколо відкритого інтервалу.

4) Як графік функції абсолютного значення порівнюється з графіком квадратичної функції\(y=x^2\), за збільшенням і зменшенням інтервалів?

алгебраїчна

Для вправ 5-15 знайти середню швидкість зміни кожної функції на інтервалі, заданому для дійсних чисел\(b\) або\(h\).

5)\(f(x)=4x^2−7\) на\([1, b]\)

Відповідь

\(4(b+1)\)

6)\(g(x)=2x^2−9\) на\([4, b]\)

7)\(p(x)=3x+4\) на\([2, 2+h]\)

Відповідь

\(3\)

8)\(k(x)=4x−2\) на\([3, 3+h]\)

9)\(f(x)=2x^2+1\) на\([x,x+h]\)

Відповідь

\(4x+2h\)

10)\(g(x)=3x^2−2\) на\([x,x+h]\)

11)\(a(t)=\dfrac{1}{t+4}\) на\([9,9+h]\)

Відповідь

\(\dfrac{−1}{13(13+h)}\)

12)\(b(x)=1x+3\) на\([1,1+h]\)

13)\(j(x)=3x^3\) на\([1,1+h]\)

Відповідь

\(3h^2+9h+9\)

14)\(r(t)=4t^3\) на\([2,2+h]\)

15)\(\dfrac{f(x+h)−f(x)}{h}\) дано\(f(x)=2x^2−3x\) на\([x,x+h]\)

Відповідь

\(4x+2h−3\)

Графічний

Для вправ 16-17 розглянемо графік\(f\) показаний на малюнку нижче

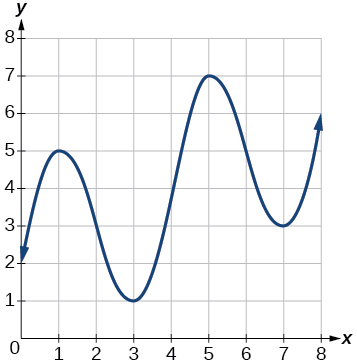
Графік многочлена.

16) Оцініть середню швидкість зміни від\(x=1\) до\(x=4\).

17) Оцініть середню швидкість зміни від\(x=2\) до\(x=5\).

Відповідь

\(\dfrac{4}{3}\)

Для наступних вправ використовуйте графік кожної функції для оцінки інтервалів, на яких функція збільшується або зменшується.

18)

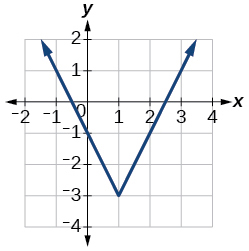
19)

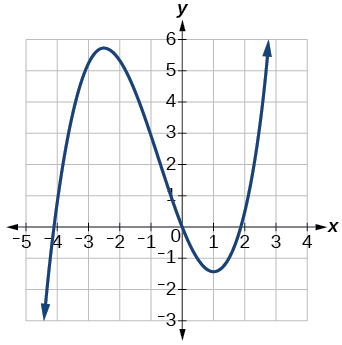
Відповідь

збільшуючи на\((−\infty,−2.5)\cup(1,\infty)\), зменшуючи на\((−2.5, 1)\)

20)

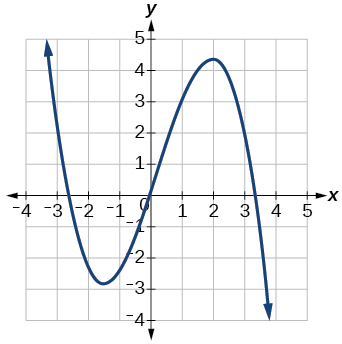
21)

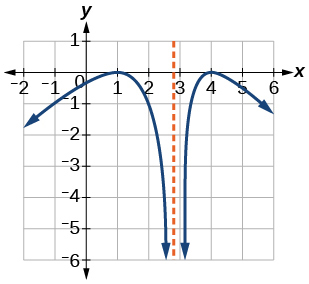
Відповідь

збільшуючи на\((−\infty,1)\cup(3,4)\), зменшуючи на\((1,3)\cup(4,\infty)\)

Для вправ 22-23 розглянемо графік, показаний на малюнку нижче.

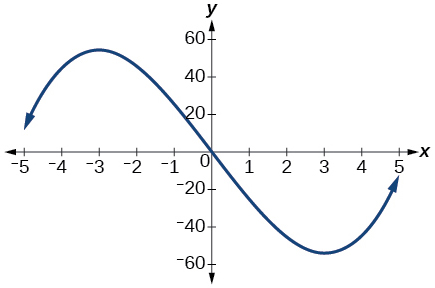
Графік кубічної функції.

22) Оцініть інтервали, де функція збільшується або зменшується.

23) Оцініть точку (и), в якій графік f має локальний максимум або локальний мінімум.

Відповідь

локальний максимум:\((−3, 60)\), місцевий мінімум:\((3, −60)\)

Для вправ 24-25 розглянемо графік на малюнку нижче.

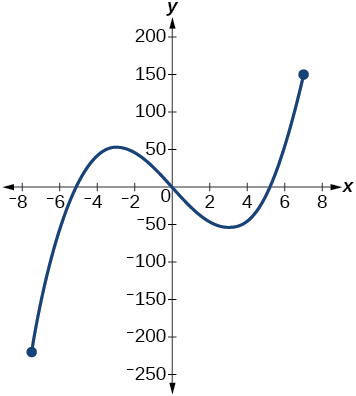
Графік кубічної функції.

24) Якщо показаний повний графік функції, оцініть інтервали, де функція збільшується або зменшується.

25) Якщо показаний повний графік функції, оцініть абсолютний максимум і абсолютний мінімум.

Відповідь

абсолютний максимум приблизно\((7, 150)\), абсолютний мінімум приблизно\((−7.5, −220)\)

Числові

26) У таблиці нижче наведено річний обсяг продажів (в мільйоні доларів) продукту з 1998 по 2006 рік. Яким був середній темп зміни річних продажів (а) між 2001 та 2002 роками та (б) між 2001 та 2004 роками?

Рік	Продажі (мільйони доларів)
1998	201
1999	219
2000	233
2001	243
2002	249
2003	251
2004	249
2005	243
2006	233

27) У таблиці нижче наведено чисельність населення міста (в тисячах) з 2000 по 2008 рік. Яким був середній темп зміни населення (а) між 2002 і 2004 роками та (б) між 2002 та 2006 роками?

Рік	Населення (тис.)
2000	87
2001	84
2002	83
2003	80
2004	77
2005	76
2006	78
2007	81
2008	85

Відповідь

а.\(-3000\); б.\(-1250\)

Для вправ 28-34 знайти середню швидкість зміни кожної функції на заданому інтервалі.

28)\(f(x)=x^2\) на\([1, 5]\)

29)\(h(x)=5−2x^2\) на\([−2,4]\)

Відповідь

\(-4\)

30)\(q(x)=x^3\) на\([−4,2]\)

31)\(g(x)=3x^3−1\) на\([−3,3]\)

Відповідь

\(27\)

32)\(y=\dfrac{1}{x}\) на\([1, 3]\)

33)\(p(t)=\dfrac{(t^2-4)(t+1)}{t^2+3}\) на\([-3,1]\)

Відповідь

\(-0.167\)

34)\(k(t)=6t^2+\dfrac{4}{t^3}\) на\([−1,3]\)

Технологія

Для вправ 35-40 використовуйте графічну утиліту для оцінки локальних екстремумів кожної функції та оцінки інтервалів, на яких функція збільшується і зменшується.

35)\(f(x)=x^4−4x^3+5\)

Відповідь

Локальний мінімум при\((3,−22)\), зменшується на\((−\infty, 3)\), збільшується на\((3, \infty)\)

36)\(h(x)=x^5+5x^4+10x^3+10x^2−1\)

37)\(g(t)=t\sqrt{t+3}\)

Відповідь

Локальний мінімум при\((−2,−2)\), зменшується на\((−3,−2)\), збільшується на\((−2, \infty)\)

38)\(k(t)=3t^{\frac{2}{3}}−t\)

39)\(m(x)=x^4+2x^3−12x^2−10x+4\)

Відповідь

Локальний максимум при\((−0.5, 6)\), локальні мінімуми при\((−3.25,−47)\) і\((2.1,−32)\), зменшуючи на\((−\infty,−3.25)\) і\((−0.5, 2.1)\), збільшуючи на\((−3.25, −0.5)\) і\((2.1,\infty)\)

40)\(n(x)=x^4−8x^3+18x^2−6x+2\)

Розширення

41) Графік функції\(f\) показаний на малюнку нижче:

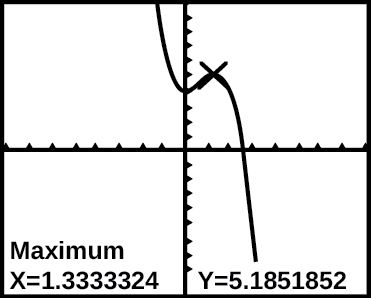
Графік f (x) на графічному калькуляторі.

На основі знімка екрана калькулятора, точка\((1.333, 5.185)\) полягає в тому, що з наступного?

1. відносний (локальний) максимум функції
2. вершина функції
3. абсолютний максимум функції
4. нуль функції

Відповідь

a

42) Нехай\(f(x)=\dfrac{1}{x}\). Знайти число\(c\) таке, що середня швидкість зміни функції f на проміжку\((1,c)\) дорівнює\(-\dfrac{1}{4}\).

43) Нехай\(f(x)=\dfrac{1}{x}\). Знайти число\(b\) таке, що середня швидкість зміни f на проміжку\((2,b)\) дорівнює\(−\dfrac{1}{10}\).

Відповідь

\(b=5\)

Реальні програми

44) На початку поїздки читається одометр на автомобілі\(21,395\). Після закінчення поїздки, через\(13.5\) години, читається одометр\(22,125\). Припустимо, що шкала на одометрі знаходиться в милі. Яку середню швидкість проїхав автомобіль під час цієї поїздки?

45) Водій автомобіля зупинився на заправці, щоб заповнити свій бензобак. Він подивився на годинник, і час читав рівно 3:40 вечора. В цей час він почав закачувати газ в резервуар. Рівно о 3:44 бак був заповнений, і він помітив, що перекачував\(10.7\) галони. Яка середня швидкість надходження бензину в бензобак?

Відповідь

\(2.7\)галонів в хвилину

46) Біля поверхні Місяця відстань, на яку падає об'єкт, є функцією часу. Це дається тим\(d(t)=2.6667t^2\), де\(t\) знаходиться в секундах і\(d(t)\) знаходиться в ногах. Якщо об'єкт скидається з певної висоти, знайдіть середню швидкість об'єкта від\(t=1\) до\(t=2\).

47) Графік на малюнку нижче ілюструє розпад радіоактивної речовини протягом декількох\(t\) днів.

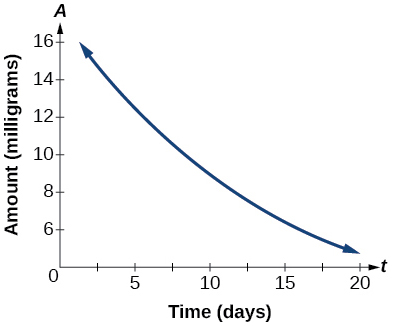
Графік експоненціальної функції.

Використовуйте графік, щоб оцінити середню швидкість розпаду від\(t=5\) до\(t=15\).

Відповідь

приблизно\(-0.6\) міліграмів на добу

1.4: Склад функцій

Припустимо, ми хочемо порахувати, скільки коштує обігрів будинку в конкретний день року. Вартість опалення будинку буде залежати від середньодобової температури, а в свою чергу, середньодобова температура залежить від конкретного дня року. Вартість залежить від температури, а температура залежить від дня. Об'єднавши ці дві зв'язки в одну функцію, ми виконали композицію функцій, яка є фокусом цього розділу.

Вербальний

1) Як знайти область частки двох функцій,\(\dfrac{f}{g}\)?

Відповідь

Знайдіть числа, які роблять функцію в знаменнику\(g\) рівним нулю, і перевірте наявність будь-яких інших обмежень домену на\(f\) і\(g\), таких як парний індексований корінь або нулі в знаменнику.

2) Який склад двох функцій,\(f{\circ}g\)?

3) Якщо порядок змінюється при складанні двох функцій, чи може результат коли-небудь бути таким же, як відповідь у вихідному порядку композиції? Якщо так, наведіть приклад. Якщо ні, поясніть, чому б і ні.

Відповідь

Так. Зразок відповіді: Нехай\(f(x)=x+1\) і\(g(x)=x−1\). Потім\(f(g(x))=f(x−1)=(x−1)+1=x\) і\(g(f(x))=g(x+1)=(x+1)−1=x\). Отже\(f{\circ}g=g{\circ}f\).

4) Як знайти домен для складу двох функцій,\(f{\circ}g\)?

алгебраїчна

5) Задано\(f(x)=x^2+2x\) і\(g(x)=6−x^2\),\(f+g\) find\(f−g\),\(fg\), і\(\dfrac{f}{g}\) .Визначте домен для кожної функції в інтервальних позначеннях.

Відповідь

\((f+g)(x)=2x+6\), домен:\((−\infty,\infty)\)

\((f−g)(x)=2x^2+2x−6\), домен:\((−\infty,\infty)\)

\((fg)(x)=−x^4−2x^3+6x^2+12x\), домен:\((−\infty,\infty)\)

\(\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},\)домен:\( (−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)\)

6) Дано\(f(x)=−3x^2+x\) і\(g(x)=5\), знайти\(f+g\),\(f−g\),\(fg\), і\(\dfrac{f}{g}\). Визначте домен для кожної функції в інтервальній нотації.

7) Дано\(f(x)=2x^2+4x\) і\(g(x)=\dfrac{1}{2x}\), знайти\(f+g\),\(f−g\),\(fg\), і\(\dfrac{f}{g}\). Визначте домен для кожної функції в інтервальній нотації.

Відповідь

\((f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}\), домен:\((−\infty,0)\cup(0,\infty)\)

\((f−g)(x)=\dfrac{4x3+8x2−1}{2x}\), домен:\((−\infty,0)\cup(0,\infty)\)

\((fg)(x)=x+2\), домен:\((−\infty,0)\cup(0,\infty)\)

\((fg)(x)=4x^3+8x^2\), домен:\((−\infty,0)\cup(0,\infty)\)

8) Дано\(f(x)=\dfrac{1}{x−4}\) і\(g(x)=\dfrac{1}{6−x}\), знайти\(f+g\),\(f−g\),\(fg\), і\(\dfrac{f}{g}\). Визначте домен для кожної функції в інтервальній нотації.

9) Дано\(f(x)=3x^2\) і\(g(x)=\sqrt{x−5}\), знайти\(f+g\),\(f−g\),\(fg\), і\(\dfrac{f}{g}\). Визначте домен для кожної функції в інтервальній нотації.

Відповідь

\((f+g)(x)=3x^2+\sqrt{x−5}\), домен:\(\left[5,\infty\right)\)

\((f−g)(x)=3x^2−\sqrt{x−5}\), домен:\(\left[5,\infty\right)\)

\((fg)(x)=3x^2\sqrt{x−5}\), домен:\(\left[5,\infty\right)\)

\(\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}\), домен:\((5,\infty)\)

10) Дано\(f(x)=\sqrt{x}\) і\(g(x)=|x−3|\), знайдіть\(\dfrac{g}{f}\). Визначте область функції в інтервальних позначеннях.

11) Задано\(f(x)=2x^2+1\) і\(g(x)=3x−5\), знайдіть наступне:

1. \(f(g(2))\)
2. \(f(g(x))\)
3. \(g(f(x))\)
4. \((g{\circ}g)(x)\)
5. \((f{\circ}f)(−2)\)

Відповідь

1. \(3\)
2. \(f(g(x))=2(3x−5)^2+1\)
3. \(f(g(x))=6x^2−2\)
4. \((g{\circ}g)(x)=3(3x−5)−5=9x−20\)
5. \((f{\circ}f)(−2)=163\)

Для вправ 12-17 використовуйте кожну пару функцій, щоб знайти\(f(g(x))\) і\(g(f(x))\). Спростіть свої відповіді.

12)\(f(x)=x^2+1\),\(g(x)=\sqrt{x+2}\)

13)\(f(x)=\sqrt{x}+2\),\(g(x)=x^2+3\)

Відповідь

\(f(g(x))=\sqrt{x+3}\),\(g(f(x))=x+4\sqrt{x}+7\)

14)\(f(x)=|x|\),\(g(x)=5x+1\)

15)\(f(x)=\sqrt[3]{x}\),\(g(x)=\dfrac{x+1}{x^3}\)

Відповідь

\(f(g(x))=\sqrt[3]{\dfrac{x+1}{x^3}}=\dfrac{\sqrt[3]{x+1}}{x}\),\(g(f(x))=\dfrac{\sqrt[3]{x}+1}{x}\)

16)\(f(x)=\dfrac{1}{x−6}\),\(g(x)=\dfrac{7}{x}+6\)

17)\(f(x)=\dfrac{1}{x−4}\),\(g(x)=\dfrac{2}{x}+4\)

Відповідь

\((f{\circ}g)(x)=\dfrac{1}{\frac{2}{x}+4-4}=\dfrac{x}{2}\),\((g{\circ}f)(x)=2x-4\)

Для вправ 18-25 використовуйте кожен набір функцій, щоб знайти f (g (h (x))). Спростіть свої відповіді.

18)\(f(x)=x^4+6\),\(g(x)=x−6\), і\(h(x)=\sqrt{x}\)

19)\(f(x)=x^2+1\),\(g(x)=\dfrac{1}{x}\), і\(h(x)=x+3\)

Відповідь

\(f(g(h(x)))=\left(\dfrac{1}{x+3}\right)^2+1\)

20) Дано\(f(x)=\dfrac{1}{x}\) і\(g(x)=x−3\), знайдіть наступне:

1. \((f{\circ}g)(x)\)
2. домен\((f{\circ}g)(x)\) в інтервальній нотації
3. \((g{\circ}f)(x)\)
4. домен\((g{\circ}f)(x)\)
5. \(\left(\dfrac{f}{g}\right)x\)

21) Дано\(f(x)=\sqrt{2−4x}\) і\(g(x)=−\dfrac{3}{x}\), знайдіть наступне:

1. \((g{\circ}f)(x)\)
2. домен\((g{\circ}f)(x)\) в інтервальній нотації

Відповідь

1. \((g{\circ}f)(x)=−\dfrac{3}{\sqrt{2−4x}}\)
2. \(\left(−\infty,\dfrac{1}{2}\right)\)

22) З огляду на функції\(f(x)=\dfrac{1−x}{x}\) і\(g(x)=\dfrac{1}{1+x^2}\), знайдіть наступне:

1. \((g{\circ}f)(x)\)
2. \((g{\circ}f)(2)\)

23) Задані функції\(p(x)=\dfrac{1}{\sqrt{x}}\) та\(m(x)=x^2−4\), вкажіть область кожної з наступних функцій за допомогою інтервальних позначень:

1. \(\dfrac{p(x)}{m(x)}\)
2. \(p(m(x))\)
3. \(m(p(x))\)

Відповідь

1. \((0,2)\cup(2,\infty)\)
2. \((−\infty,−2)\cup(2,\infty)\)
3. \((0,\infty)\)

24) Задані функції\(q(x)=\dfrac{1}{\sqrt{x}}\) та\(h(x)=x^2−9\), стан області кожної з наступних функцій за допомогою інтервальних позначень.

1. \(\dfrac{q(x)}{h(x)}\)
2. \(q(h(x))\)
3. \(h(q(x))\)

25) Для\(f(x)=\dfrac{1}{x}\) і\(g(x)=\sqrt{x−1}\), запишіть домен\((f{\circ}g)(x)\) в інтервальному позначенні.

Відповідь

\((1,\infty)\)

Для вправ 26-41 знайдіть функції\(f(x)\) і\(g(x)\) тому задану функцію можна виразити як\(h(x)=f(g(x))\).

26)\(h(x)=(x+2)^2\)

27)\(h(x)=(x−5)^3\)

Відповідь

зразок:\(f(x)=x^3\)

\(g(x)=x−5\)

28)\(h(x)=\dfrac{3}{x−5}\)

29)\(h(x)=\dfrac{4}{(x+2)^2}\)

Відповідь

зразок:\(f(x)=\dfrac{4}{x}\)

\(g(x)=(x+2)^2\)

30)\(h(x)=4+\sqrt[3]{x}\)

31)\(h(x)=\sqrt[3]{\dfrac{1}{2x−3}}\)

Відповідь

зразок:\(f(x)=\sqrt[3]{x}\)

\(g(x)=\dfrac{1}{2x−3}\)

32)\(h(x)=\dfrac{1}{(3x^2−4)^{−3}}\)

33)\(h(x)=\sqrt[4]{\dfrac{3x−2}{x+5}}\)

Відповідь

зразок:\(f(x)=\sqrt[4]{x}\)

\(g(x)=\dfrac{3x−2}{x+5}\)

34)\(h(x)=(\dfrac{8+x^3}{8−x^3})^4\)

35)\(h(x)=\sqrt{2x+6}\)

Відповідь

зразок:\(f(x)=\sqrt{x}\)

\(g(x)=2x+6\)

36)\(h(x)=(5x−1)^3\)

37)\(h(x)=\sqrt[3]{x−1}\)

Відповідь

зразок:\(f(x)=\sqrt[3]{x}\)
\(g(x)=(x−1)\)

38)\(h(x)=|x^2+7|\)

39)\(h(x)=\dfrac{1}{(x−2)^3}\)

Відповідь

зразок:\(f(x)=x^3\)
\(g(x)=\dfrac{1}{x−2}\)

40)\(h(x)=\left(\dfrac{1}{2x−3}\right)^2\)

41)\(h(x)=\sqrt { \dfrac{2x−1}{3x+4}}\)

Відповідь

зразок:\(f(x)=\sqrt{x}\)
\(g(x)=\dfrac{2x−1}{3x+4}\)

Графічний

Для вправ 42-49 використовуйте графіки\(f\), наведені на малюнку 1, і\(g\), показані на малюнку 2, для оцінки виразів.

Малюнок 1: Графік функції.

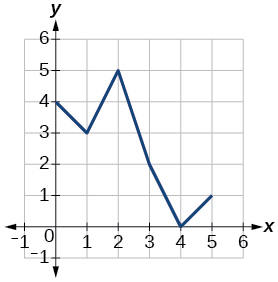
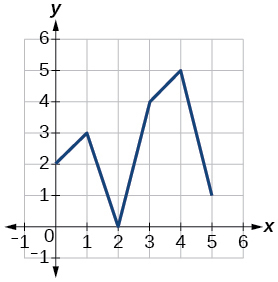
Малюнок 2: Графік функції.

42)\(f(g(3))\)

43)\(f(g(1))\)

Відповідь

\(2\)

44)\(g(f(1))\)

45)\(g(f(0))\)

Відповідь

\(5\)

46)\(f(f(5))\)

47)\(f(f(4))\)

Відповідь

\(4\)

48)\(g(g(2))\)

49)\(g(g(0))\)

Відповідь

\(0\)

Для виконання вправ 50-57 використовуйте графіки\(f(x)\), наведені на малюнку 3\(g(x)\), показані на малюнку 4, і\(h(x)\), показані на малюнку 5, для оцінки виразів.

Малюнок 3: Графік параболи.

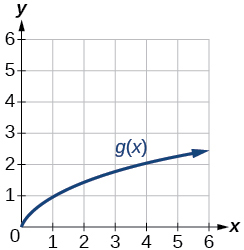
Рисунок 4: Графік функції квадратного кореня.

Малюнок 5: Графік функції абсолютного значення.

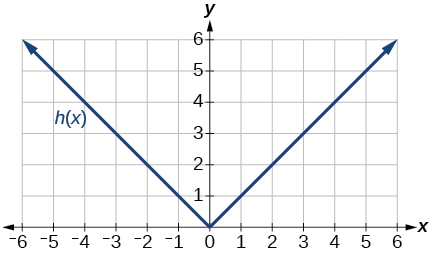
50)\(g(f(1))\)

51)\(g(f(2))\)

Відповідь

\(2\)

52)\(f(g(4))\)

53)\(f(g(1))\)

Відповідь

\(1\)

54)\(f(h(2))\)

55)\(h(f(2))\)

Відповідь

\(4\)

56)\(f(g(h(4)))\)

57)\(f(g(f(−2)))\)

Відповідь

\(4\)

Числові

Для вправ 58-65 використовуйте значення функцій для\(f\) і\(g\) наведені в таблиці нижче для оцінки кожного виразу.

\(x\)	\(f(x)\)	\(g(x)\)
\ (x\) ">0	\ (f (x)\) ">7	\ (г (х)\) ">9
\ (x\) ">1	\ (f (x)\) ">6	\ (г (х)\) ">5
\ (x\) ">2	\ (f (x)\) ">5	\ (г (х)\) ">6
\ (x\) ">3	\ (f (x)\) ">8	\ (г (х)\) ">2
\ (x\) ">4	\ (f (x)\) ">4	\ (г (х)\) ">1
\ (x\) ">5	\ (f (x)\) ">0	\ (г (х)\) ">8
\ (x\) ">6	\ (f (x)\) ">2	\ (г (х)\) ">7
\ (x\) ">7	\ (f (x)\) ">1	\ (г (х)\) ">3
\ (x\) ">8	\ (f (x)\) ">9	\ (г (х)\) ">4
\ (x\) ">9	\ (f (x)\) ">3	\ (g (x)\) ">0

58)\(f(g(8))\)

59)\(f(g(5))\)

Відповідь

\(9\)

60)\(g(f(5))\)

61)\(g(f(3))\)

Відповідь

\(4\)

62)\(f(f(4))\)

63)\(f(f(1))\)

Відповідь

\(2\)

64)\(g(g(2))\)

65)\(g(g(6))\)

Відповідь

\(3\)

Для вправ 66-71 використовуйте значення функцій для\(f\) і\(g\) наведені в таблиці нижче для оцінки виразів.

\(x\)	\(f(x)\)	\(g(x)\)
\ (x\) ">-3	\ (f (x)\) ">11	\ (г (х)\) ">-8
\ (x\) ">-2	\ (f (x)\) ">9	\ (g (x)\) ">-3
\ (x\) ">-1	\ (f (x)\) ">7	\ (g (x)\) ">0
\ (x\) ">0	\ (f (x)\) ">5	\ (г (х)\) ">1
\ (x\) ">1	\ (f (x)\) ">3	\ (g (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">1	\ (g (x)\) ">-3
\ (x\) ">3	\ (f (x)\) ">-1	\ (г (х)\) ">-8

66)\((f{\circ}g)(1)\)

67)\((f{\circ}g)(2)\)

Відповідь

\(11\)

68)\((g{\circ}f)(2)\)

69)\((g{\circ}f)(3)\)

Відповідь

\(0\)

70)\((g{\circ}g)(1)\)

71)\((f{\circ}f)(3)\)

Відповідь

\(7\)

Для вправ 72-75 використовуйте кожну пару функцій, щоб знайти\(f(g(0))\) і\(g(f(0))\).

72)\(f(x)=4x+8\),\(g(x)=7−x^2\)

73)\(f(x)=5x+7\),\(g(x)=4−2x^2\)

Відповідь

\(f(g(0))=27\),\(g(f(0))=−94\)

74)\(f(x)=\sqrt{x+4}\),\(g(x)=12−x^3\)

75)\(f(x)=\frac{1}{x+2}\),\(g(x)=4x+3\)

Відповідь

\(f(g(0))=\frac{1}{5}\),\(g(f(0))=5\)

Для вправ 76-79 використовуйте функції\(f(x)=2x^2+1\) та\(g(x)=3x+5\) оцініть або знайдіть складену функцію, як зазначено.

76)\(f(g(2))\)

77)\(f(g(x))\)

Відповідь

\(18x^2+60x+51\)

78)\(g(f(−3))\)

79)\((g{\circ}g)(x)\)

Відповідь

\(g{\circ}g(x)=9x+20\)

Розширення

Для вправ 80-84 використовують\(f(x)=x^3+1\) і\(g(x)=\sqrt[3]{x−1}\).

80) Знайти\((f{\circ}g)(x)\) і\((g{\circ}f)(x)\). Порівняйте дві відповіді.

81) Знайти\((f{\circ}g)(2)\) і\((g{\circ}f)(2)\).

Відповідь

\(2\)

82) Що таке домен\((g{\circ}f)(x)\)?

83) Що таке домен\((f{\circ}g)(x)\)?

Відповідь

\((−\infty,\infty)\)

84) Нехай\(f(x)=\frac{1}{x}\).

1. Знайти\((f{\circ}f)(x)\).
2. Чи є\((f{\circ}f)(x)\) для будь-якої функції\(f\) той самий результат, що і відповідь на частину (а) для будь-якої функції? Поясніть.

Для вправ 85-87, нехай\(F(x)=(x+1)^5\),\(f(x)=x^5\), і\(g(x)=x+1\).

85) Правда чи помилково:\((g{\circ}f)(x)=F(x)\).

Відповідь

Помилковий

86) Правда чи неправда:\((f{\circ}g)(x)=F(x)\).

Для вправ 87-89 знайдіть склад коли\(f(x)=x^2+2\) для всіх\(x\geq0\) і\(g(x)=\sqrt{x−2}\).

87)\((f{\circ}g)(6)\);\((g{\circ}f)(6)\)

Відповідь

\((f{\circ}g)(6)=6\);\((g{\circ}f)(6)=6\)

88)\((g{\circ}f)(a)\);\((f{\circ}g)(a)\)

89)\((f{\circ}g)(11)\);\((g{\circ}f)(11)\)

Відповідь

\((f{\circ}g)(11)=11\),\((g{\circ}f)(11)=11\)

Реальні програми

90) Функція\(D(p)\) видає кількість предметів, які будуть затребувані при зазначенні ціни\(p\). Виробнича собівартість\(C(x)\) - це витрати на виготовлення\(x\) виробів. Щоб визначити собівартість продукції, коли ціна є\(\$6\), ви б зробили, що з наступного?

1. Оцінити\(D(C(6))\)
2. Оцінити\(C(D(6))\)
3. Вирішити\(D(C(x))=6\)
4. Вирішити\(C(D(p))=6\)

91) Функція\(A(d)\) дає рівень болю за шкалою,\(0\) яку\(10\) відчуває пацієнт з\(d\) міліграмами знеболюючого препарату в її системі. Міліграми препарату в системі пацієнта через\(t\) хвилини моделюється\(m(t)\). Що з перерахованого нижче ви б зробили, щоб визначити, коли пацієнт буде на рівні болю\(4\)?

1. Оцінити\(A(m(4))\)
2. Оцінити\(m(A(4))\)
3. Вирішити\(A(m(t))=4\)
4. Вирішити\(m(A(d))=4\)

Відповідь

c

92) Магазин пропонує покупцям\(30\%\) знижку на ціну\(x\) обраних товарів. Потім магазин знімає додатково\(15\%\) біля каси. Напишіть\(P(x)\) цінову функцію, яка обчислює кінцеву ціну товару з точки зору початкової ціни\(x\). (Підказка: Використовуйте склад функцій, щоб знайти відповідь.)

93) Крапля дощу, що потрапила в озеро, робить кругову пульсацію. Якщо радіус, в дюймах, зростає як функція часу в хвилинах відповідно до\(r(t)=25\sqrt{t+2}\), знайдіть площу пульсації як функцію часу. Знайдіть площу пульсації за адресою\(t=2\).

Відповідь

\(A(t)=\pi(25\sqrt{t+2})^2\)і\(A(2)=\pi(25\sqrt{4})^2=2500\pi\) квадратних дюймів

94) Лісова пожежа залишає за собою ділянку трави, спаленої в розширюється круговому малюнку. Якщо радіус кола палаючої трави збільшується з часом за формулою\(r(t)=2t+1\), висловлюйте область, спалену як функцію часу,\(t\) (хвилин).

95) Використовуйте функцію, яку ви знайшли в попередній вправі, щоб знайти загальну площу, спалену через\(5\) хвилини.

Відповідь

\(A(5)=\pi(2(5)+1)2=121\pi\)квадратні одиниці

96) Радіус\(r\), в дюймах, сферичної кулі пов'язаний з об'ємом\(V\), за\(r(V)=\sqrt[3]{\frac{3V}{4\pi}}\). Повітря нагнітається в балон, тому обсяг через\(t\) секунди задається\(V(t)=10+20t\).

1. Знайдіть складену функцію\(r(V(t))\).
2. Знайдіть точний час, коли радіус досягне 10 дюймів.

97) Кількість бактерій в охолодженому харчовому продукті\(T\) задається тим\(N(T)=23T^2−56T+1\)\(3<T<33\), де знаходиться температура їжі. Коли їжа виймається з холодильника, температура задається тим\(T(t)=5t+1.5\), де\(t\) час в годинами.

1. Знайдіть складену функцію\(N(T(t))\).
2. Знайдіть час (округлення до двох знаків після коми), коли кількість бактерій досягне 6752.

Відповідь

1. \(N(T(t))=23(5t+1.5)^2−56(5t+1.5)+1\)
2. \(3.38\)годин

1.5: Трансформація функцій

Часто, коли задається задача, ми намагаємося змоделювати сценарій за допомогою математики у вигляді слів, таблиць, графіків і рівнянь. Один із методів, який ми можемо використовувати, - адаптувати основні графіки функцій інструментарію для побудови нових моделей для заданого сценарію. Існують систематичні способи зміни функцій для побудови відповідних моделей для проблем, які ми намагаємося вирішити.

Вербальний

1) При вивченні формули функції, яка є результатом множинних перетворень, як можна відрізнити горизонтальний зсув від вертикального зсуву?

Відповідь

Горизонтальний зсув виникає, коли константа додається або віднімається від вхідних даних. Вертикальний зсув виникає, коли константа додається або віднімається від вихідних даних.

2) При вивченні формули функції, яка є результатом множинних перетворень, як можна відрізнити горизонтальний розтяг від вертикальної розтяжки?

3) При вивченні формули функції, яка є результатом множинних перетворень, як можна відрізнити горизонтальне стиснення від вертикального стиснення?

Відповідь

Горизонтальне стиснення виникає, коли константа більше ніж\(1\) множиться на вхідні дані. Вертикальне стиснення призводить до того,\(1\) що\(0\) константа між і множиться на вихід.

4) При вивченні формули функції, яка є результатом множинних перетворень, як ви можете відрізнити відображення по відношенню до\(x\) -осі від відображення щодо\(y\) -осі?

5) Як можна визначити, чи є функція непарною чи парною за формулою функції?

Відповідь

Для функції\(f\) замініть (−x) для (x) in\(f(x)\). Спростити. Якщо результуюча функція збігається з вихідною функцією\(f(−x)=f(x)\), то функція парна. Якщо результуюча функція протилежна вихідній функції\(f(−x)=−f(x)\), то вихідна функція непарна. Якщо функція не однакова або протилежна, то функція не є ні непарною, ні парною.

алгебраїчна

6) Напишіть формулу для функції, отриманої при зміщенні графіка\(1\) одиниці вгору і вліво\(2\) одиниць.\(f(x)=\sqrt{x}\)

7) Напишіть формулу для функції, отриманої при зміщенні графіка\(3\) одиниць вниз і до правої\(1\) одиниці.\(f(x)=|x|\)

Відповідь

\(g(x)=|x-1|−3\)

8) Напишіть формулу для функції, отриманої при зміщенні графіка\(4\) одиниць вниз і вправо\(3\) одиниць.\(f(x)=\dfrac{1}{x}\)

9) Напишіть формулу для функції, отриманої при зміщенні графіка\(2\) одиниць вгору і вліво\(4\) одиниць.\(f(x)=\dfrac{1}{x^2}\)

Відповідь

\(g(x)=\dfrac{1}{(x+4)^2}+2\)

Для вправ 10-19 опишіть, як графік функції є перетворенням графіка вихідної функції\(f\).

10)\(y=f(x−49)\)

11)\(y=f(x+43)\)

Відповідь

Графік\(f(x+43)\) являє собою горизонтальний зсув вліво\(43\) одиниць графіка\(f\).

12)\(y=f(x+3)\)

13)\(y=f(x−4)\)

Відповідь

Графік\(f(x-4)\) являє собою горизонтальний зсув вправо\(4\) одиниць графіка\(f\).

14)\(y=f(x)+5\)

15)\(y=f(x)+8\)

Відповідь

Графік\(f(x)+8\) являє собою вертикальний зсув вгору\(8\) одиниць графіка\(f\).

16)\(y=f(x)−2\)

17)\(y=f(x)−7\)

Відповідь

Графік\(f(x)−7\) являє собою вертикальний зсув вниз\(7\) одиниць графіка\(f\).

18)\(y=f(x−2)+3\)

19)\(y=f(x+4)−1\)

Відповідь

Графік\(f(x+4)−1\) являє собою горизонтальний зсув вліво\(4\) одиниць і вертикальний зсув вниз\(1\) одиниці графа\(f\).

Для вправ 20-23 визначте інтервал (и), на якому функція збільшується і зменшується.

20)\(f(x)=4(x+1)^2−5\)

21)\(g(x)=5(x+3)^2−2\)

Відповідь

зменшується\((−\infty,−3)\) і збільшується на\((−3,\infty)\)

22)\(a(x)=\sqrt{−x+4}\)

23)\(k(x)=−3\sqrt{x}−1\)

Відповідь

знижуючись на\((0, \infty)\)

Графічний

Для вправ 24-26 використовуйте графік,\(f(x)=2^x\) показаний на малюнку нижче, щоб намалювати графік кожного перетворення\(f(x)\).

\ (f (x)\).» стиль = "ширина: 301px; висота: 306 пікселів;» ширина = «301px» висота = «306px» src=» https://math.libretexts.org/@api/dek..._01_05_201.jpg "/>

Графік\(f(x)\).

25)\(h(x)=2^x−3\)

24)\(g(x)=2^x+1\)

Відповідь

\ (k (x)\)» src=» https://math.libretexts.org/@api/dek..._01_05_202.jpg "/>

Графік\(k(x)\)

26)\(w(x)=2^x−1\)

Для вправ 27-30 намалюйте графік функції як перетворення графіка однієї з функцій інструментарію.

27)\(f(t)=(t+1)^2−3\)

Відповідь

\ (f (t)\).» src=» https://math.libretexts.org/@api/dek..._01_05_206.jpg "/>

Графік\(f(t)\).

28)\(h(x)=|x−1|+4\)

29)\(k(x)=(x−2)^3−1\)

Відповідь

\ (k (x)\).» src=» https://math.libretexts.org/@api/dek..._01_05_208.jpg "/>

Графік\(k(x)\).

30)\(m(t)=3+\sqrt{t+2}\)

Числові

31) Табличні уявлення для функцій\(f\)\(g\), і\(h\) наведені нижче. Пишіть\(g(x)\) і\(h(x)\) як перетворення\(f(x)\).

\(x\)	-2	-1	0	1	2
\(f(x)\)	-2	-1	-3	1	2

\(x\)	-1	0	1	2	3
\(g(x)\)	-2	-1	-3	1	2

\(x\)	-2	-1	0	1	2
\(h(x)\)	-1	0	-2	2	3

Відповідь

\(g(x)=f(x-1)\),\(h(x)=f(x)+1\)

32) Табличні уявлення для функцій\(f\)\(g\), і\(h\) наведені нижче. Пишіть\(g(x)\) і\(h(x)\) як перетворення\(f(x)\).

\(x\)	-2	-1	0	1	2
\(f(x)\)	-1	-3	4	2	1

\(x\)	-3	-2	-1	0	1
\(g(x)\)	-1	-3	4	2	1

\(x\)	-2	-1	0	1	2
\(h(x)\)	-2	-4	3	1	0

Для вправ 33-40 напишіть рівняння для кожної графічної функції, використовуючи перетворення графіків однієї з функцій інструментарію.

33)

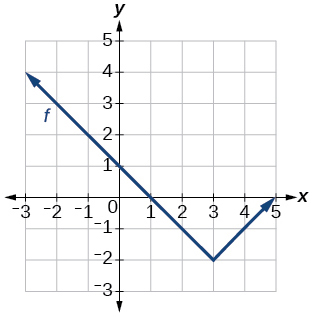
Графік абсолютної функції.

Відповідь

\(f(x)=|x-3|−2\)

34)

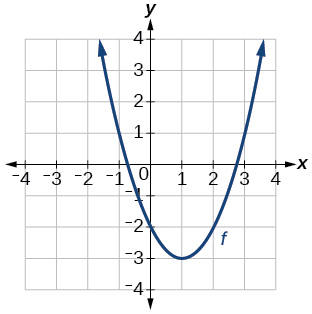
Графік параболи.

35)

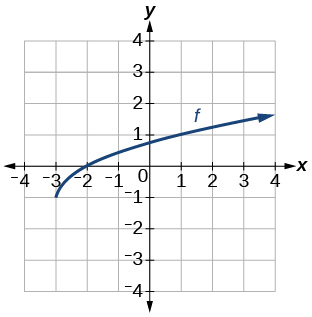
Графік функції квадратного кореня.

Відповідь

\(f(x)=\sqrt{x+3}−1\)

36)

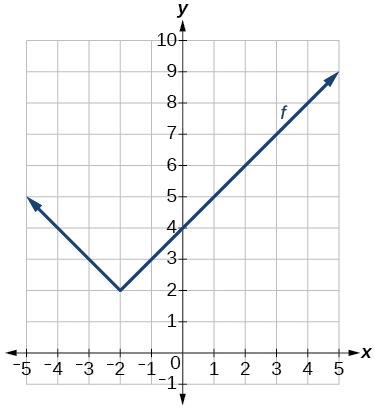
Графік абсолютної функції.

37)

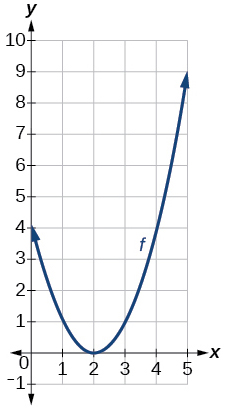
Графік параболи

Відповідь

\(f(x)=(x-2)^2\)

38)

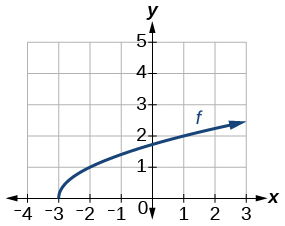
Графік функції квадратного кореня.

39)

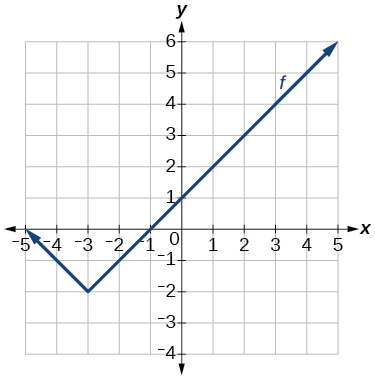
Графік абсолютної функції.

Відповідь

\(f(x)=|x+3|−2\)

40)

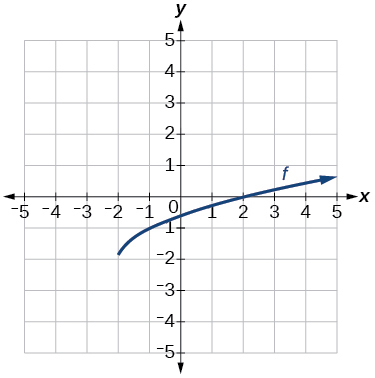
Графік функції квадратного кореня.

Для вправ 41-42 використовуйте графіки перетворень функції квадратного кореня, щоб знайти формулу для кожної з функцій.

41)

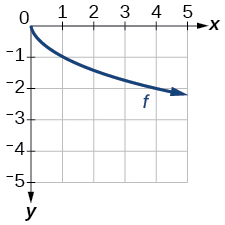
Графік функції квадратного кореня.

Відповідь

\(f(x)=−\sqrt{x}\)

42)

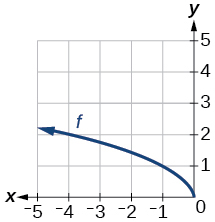
Графік функції квадратного кореня.

Для вправ 43-46 використовуйте графіки перетворених функцій інструментарію, щоб написати формулу для кожної з результуючих функцій.

43)

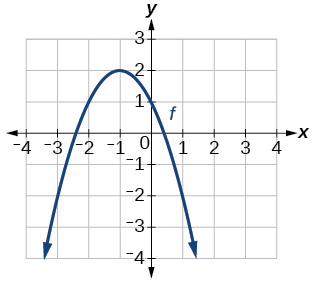
Графік параболи.

Відповідь

\(f(x)=−(x+1)^2+2\)

44)

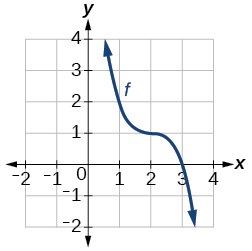
Графік кубічної функції.

45)

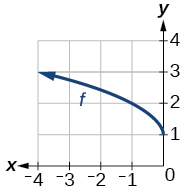
Графік функції квадратного кореня.

Відповідь

\(f(x)=\sqrt{−x}+1\)

46)

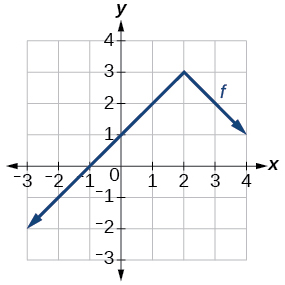
Графік абсолютної функції.

Для вправ 47-52 визначте, чи є функція непарною, парною або ні.

47)\(f(x)=3x^4\)

Відповідь

навіть

48)\(g(x)=\sqrt{x}\)

49)\(h(x)=\dfrac{1}{x}+3x\)

Відповідь

дивно

50)\(f(x)=(x−2)^2\)

51)\(g(x)=2x^4\)

Відповідь

навіть

52)\(h(x)=2x−x^3\)

Для вправ 53-62 опишіть, як графік кожної функції є перетворенням графіка вихідної функції\(f\).

53)\(g(x)=−f(x)\)

Відповідь

Графік\(g\) являє собою вертикальне відображення (поперек осі х) графа\(f\).

54)\(g(x)=f(−x)\)

55)\(g(x)=4f(x)\)

Відповідь

Графік\(g\) є вертикальним розтягуванням в 4 рази від графіка\(f\).

56)\(g(x)=6f(x)\)

57)\(g(x)=f(5x)\)

Відповідь

Графік\(g\) являє собою горизонтальне стиснення на коефіцієнт графа\(f\).\(15\)

58)\(g(x)=f(2x)\)

59)\(g(x)=f \left(\dfrac{1}{3}x \right)\)

Відповідь

Графік\(g\) є горизонтальним розтягуванням в 3 рази від графіка\(f\).

60)\(g(x)=f \left(\dfrac{1}{5}x \right)\)

61)\(g(x)=3f(−x)\)

Відповідь

Графік\(g\) являє собою горизонтальне відображення поперек осі y і вертикальне розтягування в 3 рази від графіка\(f\).

62)\(g(x)=−f(3x)\)

Для вправ 63-68 напишіть формулу для функції,\(g\) яка призводить до перетворення графіка заданої функції інструментарію, як описано.

63) Графік\(f(x)=|x|\) відбивається над\(y\) -віссю і горизонтально стискається в коефіцієнт\(\dfrac{1}{4}\).

Відповідь

\(g(x)=|−4x|\)

64) Графік\(f(x)=\sqrt{x}\) відбивається над\(x\) -віссю і горизонтально розтягується на коефіцієнт\(2\).

65) Графік вертикально\(f(x)=\dfrac{1}{x^2}\) стискається в множник\(\dfrac{1}{3}\), потім зміщується вліво\(2\) одиниць і вниз\(3\) одиниць.

Відповідь

\(g(x)=\dfrac{1}{3(x+2)^2}−3\)

66) Графік вертикально розтягується на коефіцієнт\(8\), потім зміщується вправо\(4\) одиниць і вгору\(2\) одиниць.\(f(x)=\dfrac{1}{x}\)

67) Графік вертикально\(f(x)=x^2\) стискається в множник\(\dfrac{1}{2}\), потім зміщується вправо\(5\) одиниць і вгору\(1\) одиниці.

Відповідь

\(g(x)=\dfrac{1}{2}(x-5)^2+1\)

68) Графік горизонтально розтягується на коефіцієнт\(3\), потім зміщується вліво\(4\) одиниць і вниз\(3\) одиниць.\(f(x)=x^2\)

Для вправ 69-77 опишіть, як формула є перетворенням функції інструментарію. Потім накидайте графік перетворення.

69)\(g(x)=4(x+1)^2−5\)

Відповідь

Графік функції\(f(x)=x^2\) зсувається в ліву\(1\) одиницю, розтягується вертикально на множник\(4\), і зміщений вниз\(5\) одиниць.

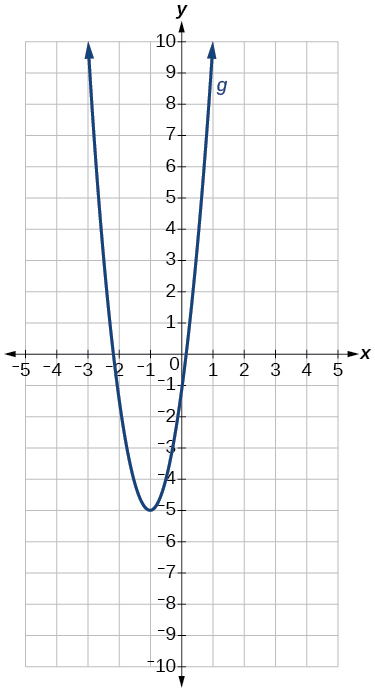
Графік параболи.

70)\(g(x)=5(x+3)^2−2\)

71)\(h(x)=−2|x−4|+3\)

Відповідь

Графік\(f(x)=|x|\) витягується вертикально на коефіцієнт\(2\), зміщений по горизонталі\(4\) одиниць вправо, відбивається поперек горизонтальної осі, а потім зміщується вертикально\(3\) одиницями вгору.

Графік функції абсолютного значення.

72)\(k(x)=−3\sqrt{x}−1\)

73)\(m(x)=\dfrac{1}{2}x^3\)

Відповідь

Графік функції\(f(x)=x^3\) стискається вертикально в множник\(\dfrac{1}{2}\).

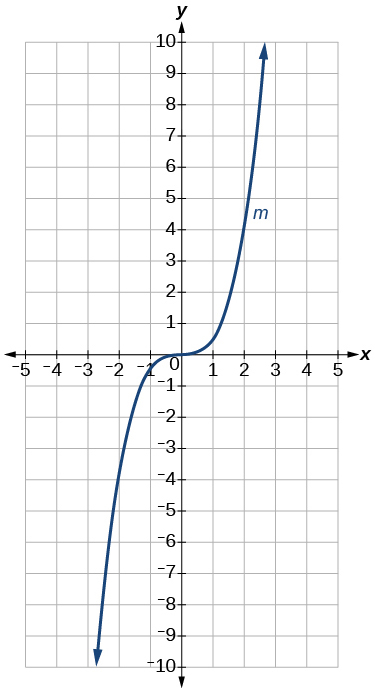
Графік кубічної функції.

74)\(n(x)=\dfrac{1}{3}|x−2|\)

75)\(p(x)=(\dfrac{1}{3}x)^3−3\)

Відповідь

Графік функції розтягується горизонтально на множник,\(3\) а потім зміщується вертикально вниз на\(3\) одиниці.

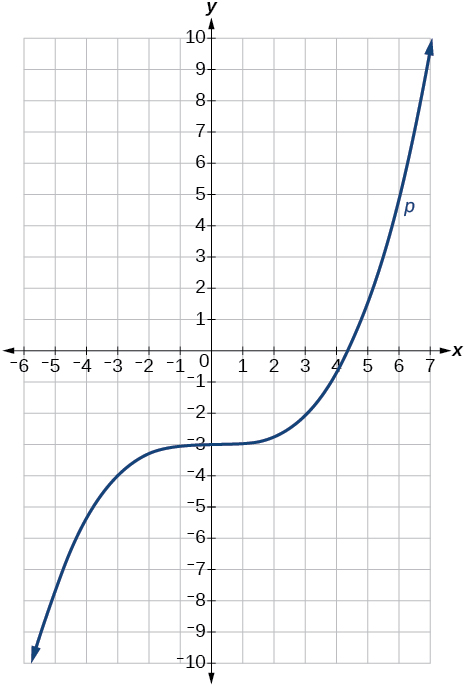
Графік кубічної функції.

76)\(q(x)=(\dfrac{1}{4}x)^3+1\)

77)\(a(x)=\sqrt{−x+4}\)

Відповідь

Графік\(f(x)=\sqrt{x}\) зміщується вправо\(4\) одиниць, а потім відбивається по вертикалі\(x=4\).

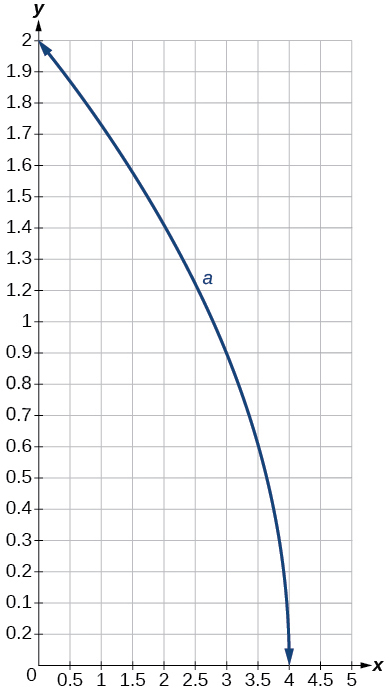
Графік функції квадратного кореня.

Для вправ 78-81 використовуйте графік на малюнку нижче, щоб накидати задані перетворення.

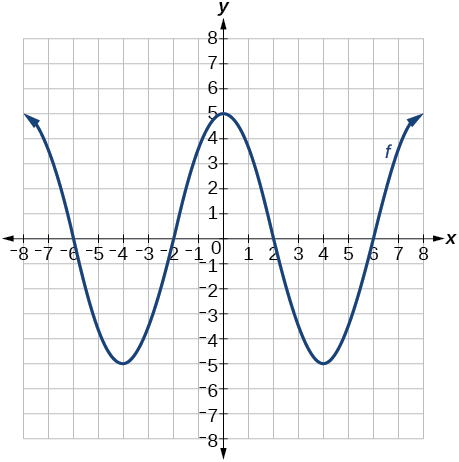
Графік многочлена.

78)\(g(x)=f(x)−2\)

79)\(g(x)=−f(x)\)

Відповідь

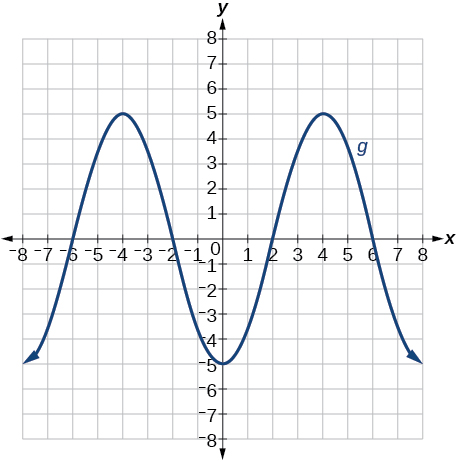
Графік многочлена.

80)\(g(x)=f(x+1)\)

81)\(g(x)=f(x−2)\)

Відповідь

Графік многочлена.

1.6: Функції абсолютних значень

Відстані у Всесвіті можна виміряти у всіх напрямках. Таким чином, корисно розглядати відстань як функцію абсолютного значення. У цьому розділі ми будемо досліджувати функції абсолютних значень. Функція абсолютного значення зазвичай вважається забезпеченням відстані числа від нуля на числовому рядку. Алгебраїчно, для будь-якого вхідного значення, виходом є значення без урахування знака.

Вербальний

1) Як ви вирішуєте рівняння абсолютного значення?

Відповідь

Виділіть абсолютне значення, щоб рівняння було вигляду\(|A|=B\). Сформуйте одне рівняння, встановивши вираз всередині символу абсолютного значення\(A\), рівне виразу з іншого боку рівняння,\(B\). Сформуйте друге рівняння, встановивши\(A\) рівне протилежному виразу на іншій стороні рівняння,\(−B\). Розв'яжіть кожне рівняння для змінної.

2) Як ви можете визначити, чи має функція абсолютного значення два\(x\) -перехоплення без графіків функції?

3) При розв'язанні функції абсолютного значення ізольований абсолютний величина дорівнює від'ємному числу. Що це говорить вам про графік функції абсолютного значення?

Відповідь

Графік функції абсолютного значення не перетинає\(x\) -вісь, тому графік або повністю вище, або повністю нижче\(x\) -осі.

4) Як можна використовувати графік функції абсолютного значення для визначення\(x\) -значень, для яких значення функції від'ємні?

5) Як ви вирішуєте абсолютну величину нерівності алгебраїчно?

Відповідь

Спочатку визначають граничні точки, знайшовши рішення (и) рівняння. Використовуйте граничні точки для формування можливих інтервалів розв'язку. Виберіть тестове значення в кожному інтервалі, щоб визначити, які значення задовольняють нерівності.

алгебраїчна

6) Опишіть всі числа\(x\), які знаходяться на відстані\(4\) від числа\(8\). Висловіть це за допомогою позначення абсолютних значень.

7) Опишіть всі числа\(x\), які знаходяться на відстані\(\dfrac{1}{2}\) від числа\(-4\). Висловіть це за допомогою позначення абсолютних значень.

Відповідь

\(|x+4|= \dfrac{1}{2}\)

8) Опишіть ситуацію, в якій відстань, від якої\(x\) знаходиться точка,\(10\) становить не менше\(15\) одиниць. Висловіть це за допомогою позначення абсолютних значень.

9) Знайти всі значення функції\(f(x)\) такі, щоб відстань від\(f(x)\) до значення\(8\) було менше\(0.03\) одиниць. Висловіть це за допомогою позначення абсолютних значень.

Відповідь

\(|f(x)−8|<0.03\)

Для вправ 10-24 розв'яжіть наведені нижче рівняння і висловіть відповідь за допомогою встановлених позначень.

10)\(|x+3|=9\)

11)\(|6−x|=5\)

Відповідь

\({1,11}\)

12)\(|5x−2|=11\)

13)\(|4x−2|=11\)

Відповідь

\(\left \{\dfrac{9}{4}, \dfrac{13}{4} \right \}\)

14)\(2|4−x|=7\)

15)\(3|5−x|=5\)

Відповідь

\(\left \{\dfrac{10}{3},\dfrac{20}{3} \right \}\)

16)\(3|x+1|−4=5\)

17)\(5|x−4|−7=2\)

Відповідь

\(\left \{\dfrac{11}{5}, \dfrac{29}{5} \right \}\)

18)\(0=−|x−3|+2\)

19)\(2|x−3|+1=2\)

Відповідь

\(\left \{\dfrac{5}{2}, \dfrac{7}{2} \right \}\)

20)\(|3x−2|=7\)

21)\(|3x−2|=−7\)

Відповідь

Немає рішення

22)\(\left |\dfrac{1}{2}x−5 \right |=11\)

23)\(\left |\dfrac{1}{3}x+5 \right |=14\)

Відповідь

\(\{−57,27\}\)

24)\(−\left |\dfrac{1}{3}x+5 \right |+14=0\)

Для вправ 25-28 знайдіть\(x\) - і\(y\) -перехоплення графіків кожної функції.

25)\(f(x)=2|x+1|−10\)

Відповідь

\((0,−8)\);\((−6,0)\),\((4,0)\)

26)\(f(x)=4|x−3|+4\)

27)\(f(x)=−3|x−2|−1\)

Відповідь

\((0,−7)\); немає\(x\) -перехоплює

28)\(f(x)=−2|x+1|+6\)

Для вправ 29-36 розв'яжіть кожне нерівність і запишіть рішення в інтервальних позначеннях.

29)\(| x−2 |>10\)

Відповідь

\((−\infty,−8)\cup(12,\infty)\)

30)\(2|v−7|−4\geq42\)

31)\(|3x−4|\geq8\)

Відповідь

\(−\dfrac{4}{3}{\leq}x\leq4\)

32)\(|x−4|\geq8\)

33)\(|3x−5|\geq-13\)

Відповідь

\(\left (−\infty,− \dfrac{8}{3}\right ]\cup\left[6,\infty\right)\)

34)\(|3x−5|\geq−13\)

35)\(|\dfrac{3}{4}x−5|\geq7\)

Відповідь

\(\left (-\infty,-\dfrac{8}{3}\right ]\cup\left[16,\infty\right)\)

36)\(\left |\dfrac{3}{4}x−5 \right |+1\leq16\)

Графічний

Для вправ 37-39 наведіть графік функції абсолютного значення. Побудуйте щонайменше п'ять точок вручну для кожного графіка.

37)\(y=|x−1|\)

Відповідь

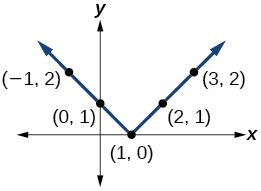
38)\(y=|x+1|\)

39)\(y=|x|+1\)

Відповідь

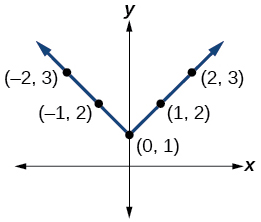
Для вправ 40-52 відведіть графік заданих функцій вручну.

40)\(y=|x|−2\)

41)\(y=−|x|\)

Відповідь

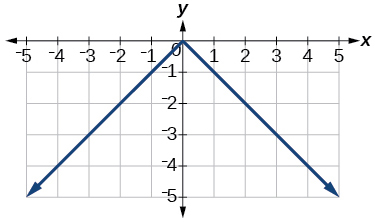
42)\(y=−|x|−2\)

43)\(y=−|x−3|−2\)

Відповідь

44)\(f(x)=−|x−1|−2\)

45)\(f(x)=−|x+3|+4\)

Відповідь

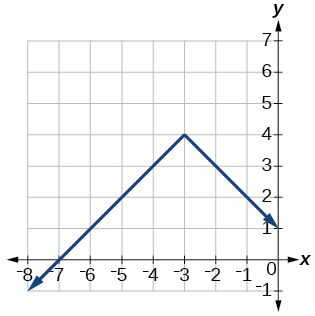
46)\(f(x)=2|x+3|+1\)

47)\(f(x)=3|x−2|+3\)

Відповідь

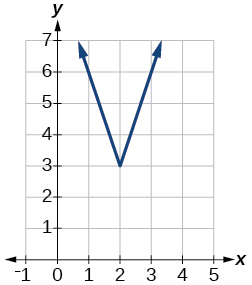
48)\(f(x)=|2x−4|−3\)

49)\(f(x)=|3x+9|+2\)

Відповідь

50)\(f(x)=−|x−1|−3\)

51)\(f(x)=−|x+4|−3\)

Відповідь

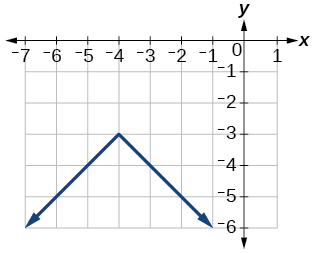
52)\(f(x)=\dfrac{1}{2}|x+4|−3\)

Технологія

53) Використовуйте графічну утиліту для\(f(x)=10|x−2|\) графіків у вікні перегляду\([0,4]\). Визначте відповідний діапазон. Показувати графік.

Відповідь

діапазон:\([0,20]\)

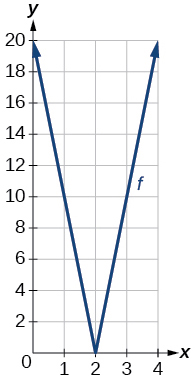
54) Використовуйте графічну утиліту для графування\(f(x)=−100|x|+100\) графіків у вікні перегляду\([−5,5]\). Визначте відповідний діапазон. Показувати графік.

Для вправ 55-56 графік кожної функції за допомогою графічної утиліти. Вкажіть оглядове вікно.

55)\(f(x)=−0.1|0.1(0.2−x)|+0.3\)

Відповідь

\(x\)-перехоплює:

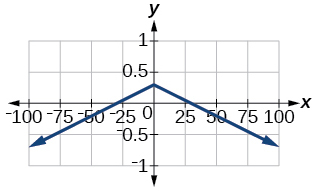
56)\(f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9\)

Розширення

Для вправ 57-59 розв'яжіть нерівність.

57)\(\left |−2x− \dfrac{2}{3}(x+1) \right |+3>−1\)

Відповідь

\((−\infty,\infty)\)

58) Якщо можливо, знайдіть всі значення такого, що не існує\(x\) -перехоплень для\(f(x)=2|x+1|+a\).

59) Якщо можливо, знайдіть всі значення такого, що не існує\(y\) -перехоплень для\(f(x)=2|x+1|+a\).

Відповідь

Немає рішення для a, яке буде тримати функцію від наявності\(y\) -intercept. Функція абсолютного значення завжди перетинає\(y\) -intercept, коли\(x=0\).

Реальні програми

60) Міста А і В знаходяться на одній лінії схід-захід. Припустимо, що місто А розташоване біля початку. Якщо відстань від міста A до міста B становить принаймні\(100\) милі і\(x\) представляє відстань від міста B до міста A, висловіть це за допомогою абсолютних значень.

61) Справжня\(p\) частка людей, які дають сприятливий рейтинг Конгресу, є\(8\%\) з похибкою\(1.5\%\). Опишіть це твердження за допомогою рівняння абсолютного значення.

Відповідь

\(|p−0.08|\leq0.015\)

62) Студенти, які наберуть в межах\(18\) балів від числа,\(82\) пройдуть певний тест. Напишіть це твердження, використовуючи позначення абсолютного значення і використовуйте змінну\(x\) для оцінки.

63) Машиніст повинен виготовити підшипник, який знаходиться в межах\(0.01\) дюймів від правильного діаметра\(5.0\) дюймів. Використовуючи в\(x\) якості діаметра підшипника, запишіть це твердження, використовуючи абсолютні значення.

Відповідь

\(|x−5.0|\leq0.01\)

64) Допуск для кулькового підшипника є\(0.01\). Якщо справжній діаметр підшипника повинен становити\(2.0\) дюйми, а виміряне значення діаметра -\(x\) дюйми, висловіть допуск, використовуючи абсолютні значення.

1.7: Зворотні функції

Якщо деякі фізичні машини можуть працювати в двох напрямках, ми можемо запитати, чи можуть деякі функції «машини», які ми вивчали, також можуть працювати назад. У цьому розділі ми розглянемо зворотний характер функцій.

Вербальний

1) Опишіть, чому тест горизонтальної лінії є ефективним способом визначити, чи є функція один до одного?

Відповідь

Кожен вихід функції повинен мати рівно один вихід, щоб функція була один до одного. Якщо будь-яка горизонтальна лінія перетинає графік функції більше одного разу, це означає, що\(y\) -значення повторюються і функція не є один-до-одному. Якщо жодна горизонтальна лінія не перетинає графік функції більше одного разу, то no\(y\) -values повторюються і функція є один до одного.

2) Чому ми обмежуємо область функції,\(f(x)=x^2\) щоб знайти зворотну функцію?

3) Чи може функція бути власною оберненою? Поясніть.

Відповідь

Так. Наприклад,\(f(x)=\dfrac{1}{x}\) є свій власний зворотний.

4) Функції «один-на-один» або завжди збільшуються, або завжди зменшуються? Чому чи чому ні?

5) Як знайти обернену функцію алгебраїчно?

Відповідь

Дано функцію\(y=f(x)\), вирішити for\(x\) в терміні\(y\). Розв'язка\(x\) і\(y\). Розв'яжіть нове рівняння для\(y\). Вираз для\(y\) - зворотне,\(y=f^{-1}(x)\).

алгебраїчна

6) Показати, що функція\(f(x)=a−x\) є власною оберненою для всіх дійсних чисел\(a\).

Для вправ 7-12 знайдіть\(f^{-1}(x)\) для кожної функції.

7)\(f(x)=x+3\)

Відповідь

\(f^{-1}(x)=x−3\)

8)\(f(x)=x+5\)

9)\(f(x)=2−x\)

Відповідь

\(f^{-1}(x)=2−x\)

10)\(f(x)=3−x\)

11)\(f(x)=\dfrac{x}{x+2}\)

Відповідь

\(f^{-1}(x)=\dfrac{−2x}{x−1}\)

12)\(f(x)=\dfrac{2x+3}{5x+4}\)

Для вправ 13-16 знайдіть область, на якій кожна функція\(f\) один-на-один і не спадає. Запишіть домен в інтервальне позначення. Потім знайдіть зворотне\(f\) обмежене для цього домену.

13)\(f(x)=(x+7)^2\)

Відповідь

домен\(f(x)\):\(\left[−7,\infty\right)\);\(f^{-1}(x)=\sqrt{x}−7\)

14)\(f(x)=(x−6)^2\)

15)\(f(x)=x^2−5\)

Відповідь

домен\(f(x)\):\(\left[0,\infty\right)\);\(f^{-1}(x)=\sqrt{x+5}\)

16) Дано\(f(x)=\dfrac{x}{2+x}\) і\(g(x)=\dfrac{2x}{1-x}:\)

1. Знайти\(f(g(x))\) і\(g(f(x))\).
2. Що говорить нам відповідь про відносини між\(f(x)\) і\(g(x)?\)

Відповідь

а.\(f(g(x))=x\) і\(g(f(x))=x\)

б Це говорить нам про те, що\(f\) і\(g\) є зворотними функціями

Для вправ 17-18 використовуйте склад функцій, щоб перевірити, що\(f(x)\) і\(g(x)\) є зворотними функціями.

17)\(f(x)=\sqrt[3]{x-1}\) і\(g(x)=x^3+1\)

Відповідь

\(f(g(x))=x\),\(g(f(x))=x\)

18)\(f(x)=−3x+5\) і\(g(x)=\dfrac{x-5}{-3}\)

Графічний

Для вправ 19-22 використовуйте утиліту графіків, щоб визначити, чи кожна функція є один до одного.

19)\(f(x)=\sqrt{x}\)

Відповідь

один-на-один

20)\(f(x)=\sqrt[3]{3x+1}\)

21)\(f(x)=−5x+1\)

Відповідь

один-на-один

22)\(f(x)=x^3−27\)

Для вправ 23-24 визначте, чи представляє графік функцію один до одного.

23)

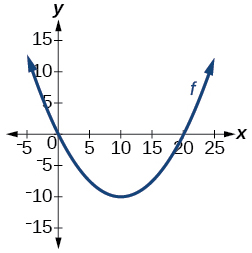
Відповідь

не один на один

24)

Малюнок нижче.

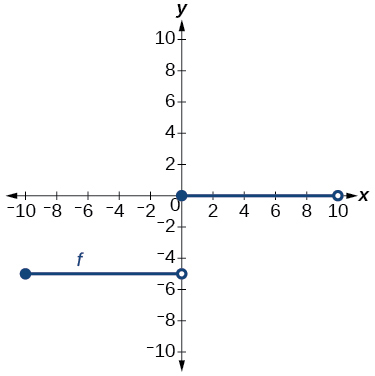
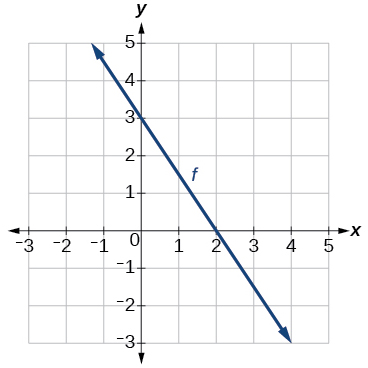
Графік прямої

25) Знайти\(f(0)\).

Відповідь

\(3\)

26) Вирішити\(f(x)=0\).

27) Знайти\(f^{-1}(0)\).

Відповідь

\(2\)

28) Вирішити\(f^{-1}(x)=0\).

Для вправ 29-32 використовуйте графік функції один до одного, показаний на малюнку нижче

Графік функції квадратного кореня.

29) Намалюйте графік\(f^{-1}\).

Відповідь

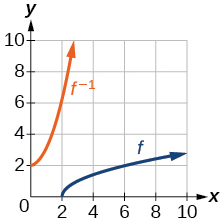
30) Знайти\(f(6)\) і\(f^{-1}(2)\).

31) Якщо\(f\) показаний повний графік, знайдіть область\(f\).

Відповідь

\([2,10]\)

32) Якщо\(f\) показаний повний графік, знайдіть діапазон\(f\)

Числові

Для вправ 33-36 оцінюйте або вирішуйте, припускаючи,\(f\) що функція один-на-один.

33) Якщо\(f(6)=7\), знайдіть\(f^{-1}(7)\).

Відповідь

\(6\)

34) Якщо\(f(3)=2\), знайдіть\(f^{-1}(2)\).

35) Якщо\(f^{-1}(−4)=−8\), знайдіть\(f(−8)\).

Відповідь

\(-4\)

36) Якщо\(f^{-1}(−2)\) =−1, знайдіть\(f(−1)\).

Для вправ 37-40 використовуйте значення, наведені в таблиці нижче, щоб оцінити або вирішити.

\(x\)	\(f(x)\)
\ (x\) ">0	\ (f (x)\) ">8
\ (x\) ">1	\ (f (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">7
\ (x\) ">3	\ (f (x)\) ">4
\ (x\) ">4	\ (f (x)\) ">2
\ (x\) ">5	\ (f (x)\) ">6
\ (x\) ">6	\ (f (x)\) ">5
\ (x\) ">7	\ (f (x)\) ">3
\ (x\) ">8	\ (f (x)\) ">9
\ (x\) ">9	\ (f (x)\) ">1

37) Знайти\(f(1)\).

Відповідь

\(0\)

38) Вирішити\(f(x)=3\).

39) Знайти\(f^{-1}(0)\).

Відповідь

\(1\)

40) Вирішити\(f^{-1}(x)=7\).

41) Скористайтеся табличним представленням\(f\) у таблиці нижче, щоб створити таблицю для\(f^{-1}(x)\).

\(x\)	3	6	9	13	14
\(f(x)\)	1	4	7	12	16

Відповідь

\(x\)	1	4	7	12	16
\(f^{-1}(x)\)	3	6	9	13	14

Технологія

Для вправ 42-44 знайдіть зворотну функцію. Потім графуйте функцію та її зворотну.

42)\(f(x)=\dfrac{3}{x-2}\)

43)\(f(x)=x^3−1\)

Відповідь

\(f^{-1}(x)=(1+x)^{1/3}\)

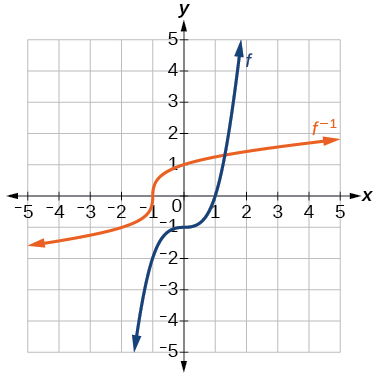
44) Знайти обернену функцію\(f(x)=\dfrac{1}{x-1}\). Використовуйте графічну утиліту, щоб знайти свій домен та діапазон. Запишіть домен і діапазон в інтервальному позначенні.

Реальні програми

45) Для перетворення з\(x\) градусів Цельсія в\(y\) градуси за Фаренгейтом використовуємо формулу\(f(x)=\dfrac{9}{5}x+32\). Знайдіть обернену функцію, якщо вона існує, і поясніть її значення.

Відповідь

\(f^{-1}(x)=\dfrac{5}{9}(x−32)\). З огляду на температуру Фаренгейта\(x\), ця формула дозволяє обчислити температуру за Цельсієм.

46)\(C\) Окружність кола - це функція його радіуса, заданого\(C(r)=2{\pi}r\). Висловіть радіус кола як функцію його окружності. Викликати цю функцію\(r(C)\). Знайдіть\(r(36\pi)\) і тлумачіть його значення.

47) Автомобіль їде з постійною швидкістю\(50\) миль на годину. Відстань, яку проїжджає автомобіль у милі, є функцією часу\(t\), у годинами, заданих\(d(t)=50t\). Знайдіть обернену функцію, висловивши час подорожі з точки зору пройденої відстані. Викликати цю функцію\(t(d)\). Знайдіть\(t(180)\) і тлумачіть його значення.

Відповідь

\(t(d)=\dfrac{d}{50}\),\(t(180)=\dfrac{180}{50}\). Час проходження автомобіля\(180\) милями становить\(3.6\) години.