1.R: Функції (огляд)
- Page ID
- 61301
1.1: Функції та позначення функцій
Для вправ 1-4 визначте, чи є відношення функцією.
1)\(\{(a,b),(c,d),(e,d)\}\)
- Відповідь
-
функція
2)\(\{(5,2),(6,1),(6,2),(4,8)\}\)
3)\(y^2+4=x\)
- Відповідь
-
не є функцією
4) Чи є графік на малюнку нижче функцією?
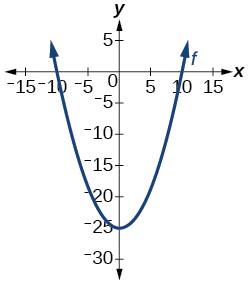
Для вправ 5-6 оцініть функцію за вказаними значеннями:\(f(-3); f(2); f(-a); -f(a); f(a+h)\)
5)\(f(x)=-2x^2+3x\)
- Відповідь
-
\(f(-3)=-27; f(2)=-2;f(-a)=-2a^2-3a;-f(a)=2a^2-3a;f(a+h)=-2a^2+3a-4ah+3h-2h^2\)
6)\(f(x)=2|3x-1|\)
Для вправ 7-8 визначте, чи є функції один-на-один.
7)\(f(x)=-3 x+5\)
- Відповідь
-
один-на-один
8)\(f(x)=|x-3|\)
Для вправ 9-11 використовуйте тест вертикальної лінії, щоб визначити, чи є відношення, графік якого надається функцією.
9)
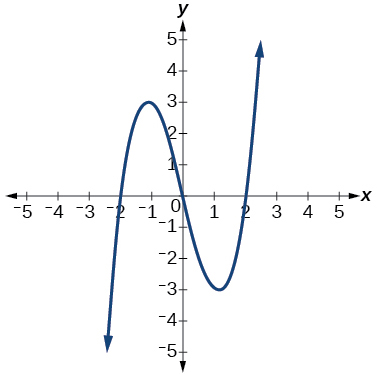
- Відповідь
-
функція
10)
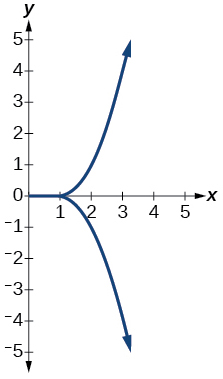
11)
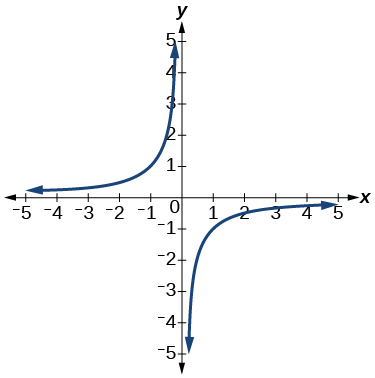
- Відповідь
-
функція
Для вправ 12-13 наведіть графік функцій.
12)\(f(x)=|x+1|\)
13)\(f(x)=x^{2}-2\)
- Відповідь
-
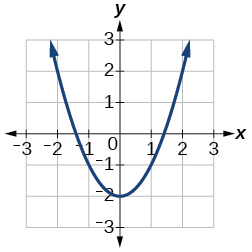
Для вправ 14-17 використовуйте малюнок нижче, щоб наблизити значення.
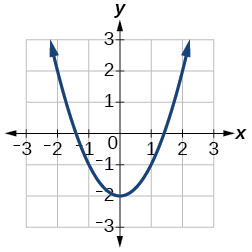
14)\(f(2)\)
15)\(f(-2)\)
- Відповідь
-
\(2\)
16) Якщо\(f(x)=-2\), то вирішуйте для\(x\)
17) Якщо\(f(x)=1\), то вирішуйте для\(x\)
- Відповідь
-
\(x=-1.8\)або\(x=1.8\)
Для вправ 18-19 скористайтеся\(h(t)=-16 t^{2}+80t\) функцією пошуку значень.
18)\(\dfrac{h(2)-h(1)}{2-1}\)
19)\(\dfrac{h(a)-h(1)}{a-1}\)
- Відповідь
-
\(\dfrac{-64+80 a-16 a^{2}}{-1+a}=-16 a+64\)
1.2: Домен і діапазон
Для вправ 1-4 знайдіть область кожної функції, висловлюючи відповіді за допомогою інтервальних позначень.
1)\(f(x)=\dfrac{2}{3 x+2}\)
2)\(f(x)=\frac{x-3}{x^{2}-4 x-12}\)
- Відповідь
-
\((-\infty,-2) \cup(-2,6) \cup(6, \infty)\)
3)
4) Графік цієї кускової функції:\(f(x)=\left\{\begin{array}{ll}{x+1} & {x<-2} \\ {-2 x-3} & {x \geq-2}\end{array}\right.\)
- Відповідь
-
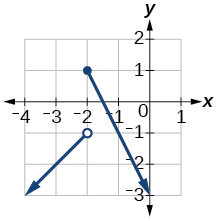
1.3: Швидкі зміни та поведінка графіків
Для вправ 1-3 знайдіть середню швидкість зміни функцій від\(x=1\) до\(x=2\)
1)\(f(x)=4 x-3\)
2)\(f(x)=10 x^{2}+x\)
- Відповідь
-
\(31\)
3)\(f(x)=-\dfrac{2}{x^{2}}\)
Для вправ 4-6 використовуйте графіки для визначення інтервалів, на яких функції збільшуються, зменшуються або постійні.
4)
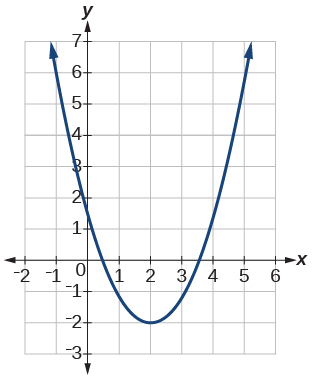
- Відповідь
-
збільшення\((2, \infty)\); зменшення\((-\infty, 2)\)
5)
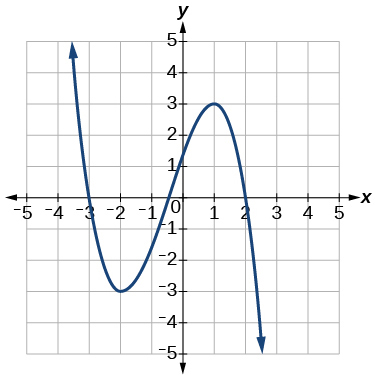
6)
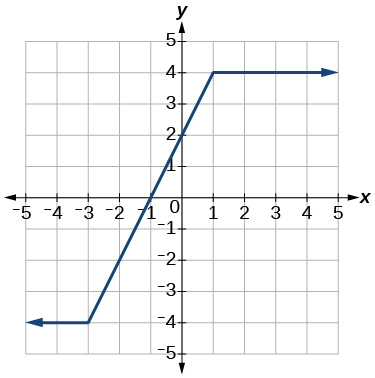
- Відповідь
-
наростаюча\((-3,1)\); постійна\((-\infty,-3) \cup(1, \infty)\)
7) Знайдіть локальний мінімум функції, розміщеної у вправі 4.
8) Знайдіть локальну крайність для функції, графічної у вправі 5.
- Відповідь
-
локальний мінімум\((-2,-3)\); локальний максимум\((1,3)\)
9) Для графіка на малюнку у вправі 10 область функції дорівнює\([-3,3]\). Асортимент є\([-10,10]\). Знайти абсолютний мінімум функції на цьому інтервалі.
10) Знайдіть абсолютний максимум функції, зображеної на малюнку нижче.
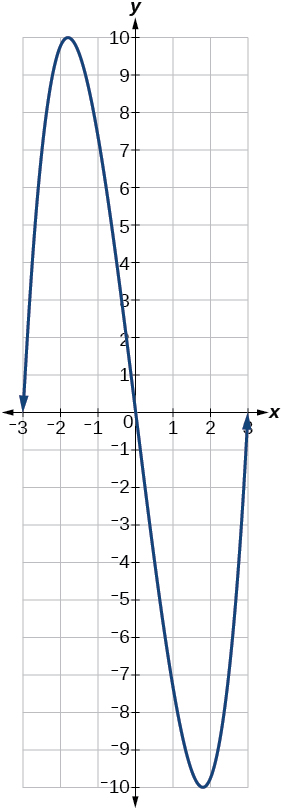
- Відповідь
-
\((-1.8,10)\)
1.4: Склад функцій
Для вправ 1-5 знайдіть\((f \circ g)(x)\) і\((g \circ f)(x)\) для кожної пари функцій.
1)\(f(x)=4-x, g(x)=-4x\)
2)\(f(x)=3 x+2, g(x)=5-6x\)
- Відповідь
-
\((f \circ g)(x)=17-18 x ;(g \circ f)(x)=-7-18x\)
3)\(f(x)=x^{2}+2 x, g(x)=5 x+1\)
4)\(f(x)=\sqrt{x+2}, g(x)=\dfrac{1}{x}\)
- Відповідь
-
\((f \circ g)(x)=\sqrt{\dfrac{1}{x}+2} ;(g \circ f)(x)=\dfrac{1}{\sqrt{x+2}}\)
5)\(f(x)=\dfrac{x+3}{2}, g(x)=\sqrt{1-x}\)
Для вправ 6-9 знайдіть\((f \circ g)\) і домен\((f \circ g)(x)\) для кожної пари функцій.
6)\(f(x)=\frac{x+1}{x+4}, g(x)=\frac{1}{x}\)
- Відповідь
-
\((f \circ g)(x)=\dfrac{1+x}{1+4 x}, x \neq 0, x \neq-\dfrac{1}{4}\)
7)\(f(x)=\dfrac{1}{x+3}, g(x)=\dfrac{1}{x-9}\)
8)\(f(x)=\dfrac{1}{x}, g(x)=\sqrt{x}\)
- Відповідь
-
\((f \circ g)(x)=\frac{1}{\sqrt{x}}, x>0\)
9)\(f(x)=\frac{1}{x^{2}-1}, g(x)=\sqrt{x+1}\)
Для вправ 10-11 висловіть кожну функцію\(H\) як склад з двох функцій\(f\) і\(g\) де\(H(x)=(f \circ g)(x)\)
10)\(H(x)=\sqrt{\frac{2 x-1}{3 x+4}}\)
- Відповідь
-
зразок:\(g(x)=\dfrac{2 x-1}{3 x+4}; f(x)=\sqrt{x}\)
11)\(H(x)=\dfrac{1}{\left(3 x^{2}-4\right)^{-3}}\)
1.5: Трансформація функцій
Для вправ 1-8 накидайте графік заданої функції.
1)\(f(x)=(x-3)^{2}\)
- Відповідь
-
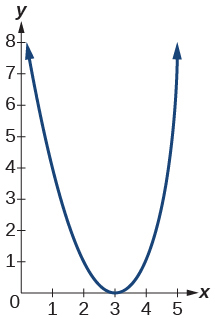
2)\(f(x)=(x+4)^{3}\)
3)\(f(x)=\sqrt{x}+5\)
- Відповідь
-
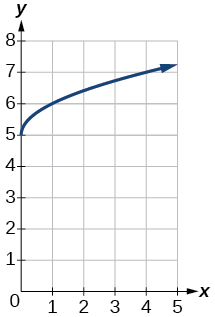
4)\(f(x)=-x^{3}\)
5)\(f(x)=\sqrt[3]{-x}\)
- Відповідь
-
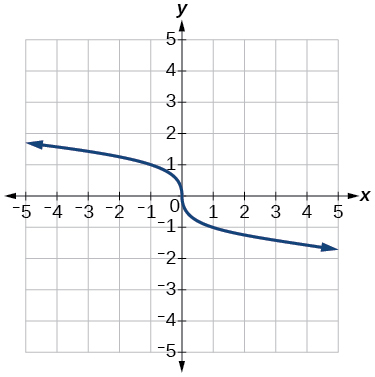
6)\(f(x)=5 \sqrt{-x}-4\)
7)\(f(x)=4[|x-2|-6]\)
- Відповідь
-
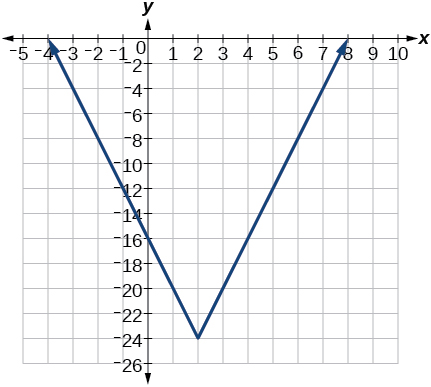
8)\(f(x)=-(x+2)^{2}-1\)
Для вправ 9-10 намалюйте графік функції,\(g\) якщо графік функції\(f\) показаний на малюнку нижче.
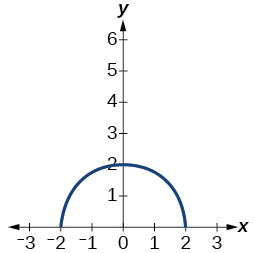
9)\(g(x)=f(x-1)\)
- Відповідь
-
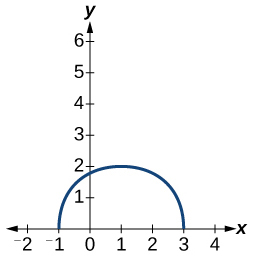
10)\(g(x)=3 f(x)\)
Для вправ 11-12 напишіть рівняння для стандартної функції, представленої кожним з наведених нижче графіків.
11)
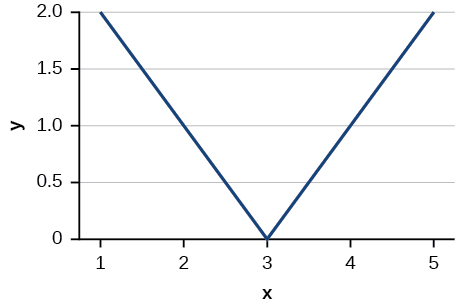
- Відповідь
-
\(f(x)=|x-3|\)
12)
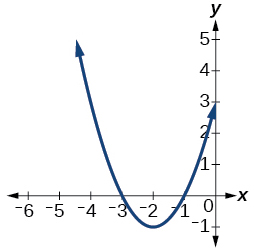
Для вправ 13-15 визначте, чи кожна функція нижче парна, непарна чи ні.
13)\(f(x)=3 x^{4}\)
- Відповідь
-
навіть
14)\(g(x)=\sqrt{x}\)
15)\(h(x)=\frac{1}{x}+3 x\)
- Відповідь
-
дивно
Для вправ 16-18 проаналізуйте графік і визначте, чи є графічна функція парною, непарною чи ні.
16)
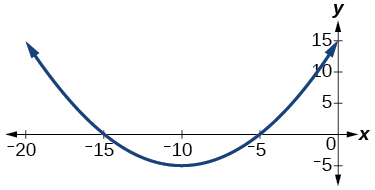
17)
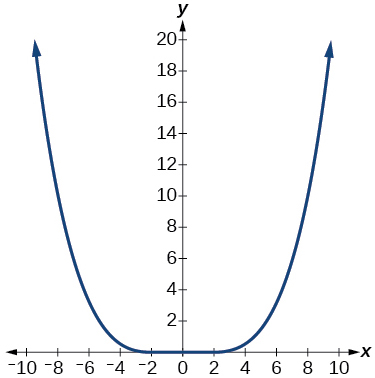
- Відповідь
-
навіть
18)
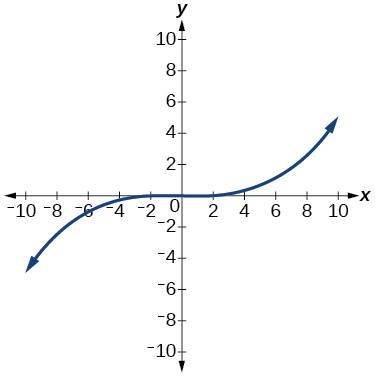
1.6: Функції абсолютних значень
Для вправ 1-3 напишіть рівняння для перетворення\(f(x)=|x|\).
1)
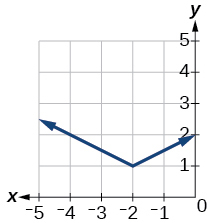
- Відповідь
-
\(f(x)=\dfrac{1}{2}|x+2|+1\)
2)
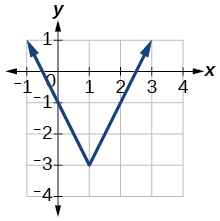
3)
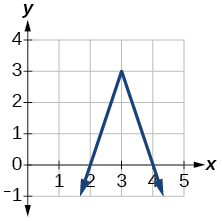
- Відповідь
-
\(f(x)=-3|x-3|+3\)
Для вправ 4-6 наведіть графік функції абсолютного значення.
4)\(f(x)=|x-5|\)
5)\(f(x)=-|x-3|\)
- Відповідь
-
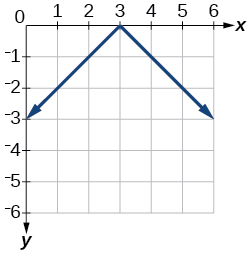
6)\(f(x)=|2 x-4|\)
Для вправ 7-8 вирішуємо рівняння абсолютного значення.
7)\(|x+4|=18\)
- Відповідь
-
\(x=-22, x=14\)
8)\(\left|\dfrac{1}{3} x+5\right|=\left|\dfrac{3}{4} x-2\right|\)
Для вправ 9-10 розв'яжіть нерівність і висловіть рішення за допомогою інтервальних позначень.
9)\(|3 x-2|<7\)
- Відповідь
-
\(\left(-\dfrac{5}{3}, 3\right)\)
10)\(\left|\dfrac{1}{3} x-2\right| \leq 7\)
1.7: Зворотні функції
Для вправ 1-2 знайдіть\(f^{-1}(x)\) для кожної функції.
1)\(f(x)=9+10 x\)
2)\(f(x)=\dfrac{x}{x+2}\)
- Відповідь
-
\(f^{-1}(x)=\dfrac{-2 x}{x-1}\)
3) Для наступної вправи знайдіть домен, на якому функція\(f\) один-на-один і не зменшується. Запишіть домен в інтервальне позначення. Потім знайдіть зворотне\(f\) обмежене для цього домену. \[f(x)=x^{2}+1\]
4) Дано\(f(x)=x^{3}-5\) і\(g(x)=\sqrt[3]{x+5} \):
- Знайти\(f(g(x))\) і\(g(f(x))\).
- Що говорить нам відповідь про відносини між\(f(x)\) і\(g(x) ?\)
- Відповідь
-
- \(f(g(x))=x\)і\(g(f(x))=x\)
- Це говорить нам про те, що\(f\) і\(g\) є зворотними функціями
Для вправ 5-8 використовуйте утиліту графіків, щоб визначити, чи кожна функція є один до одного.
5)\(f(x)=\dfrac{1}{x}\)
- Відповідь
-
Функція один-на-один.
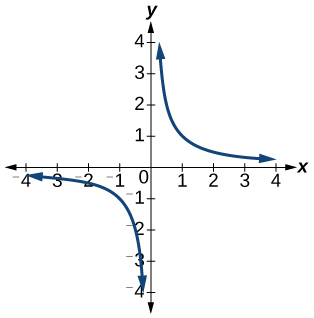
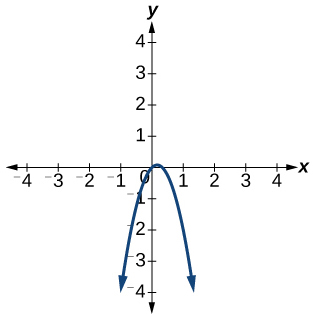
6)\(f(x)=-3 x^{2}+x\)
- Відповідь
-
Функція не є один-на-один.
7) Якщо\(f(5)=2,\) знайти\(f^{-1}(2)\)
- Відповідь
-
\(5\)
8) Якщо\(f(1)=4,\) знайти\(f^{-1}(4)\)
Практика Тест
Для вправ 1-2 визначте, чи є кожне з наступних відносин функцією.
1)\(y=2 x+8\)
- Відповідь
-
Відношення - це функція.
2)\(\{(2,1),(3,2),(-1,1),(0,-2)\}\)
Для вправ 3-4 оцініть функцію\(f(x)=-3 x^{2}+2 x\) на заданому вході.
3)\(f(-2)\)
- Відповідь
-
\(-16\)
4)\(f(a)\)
5) Покажіть, що функція\(f(x)=-2(x-1)^{2}+3\) не один-на-один.
- Відповідь
-
Графік є параболою, і графік не проходить тест горизонтальної лінії.
6) Запишіть область функції\(f(x)=\sqrt{3-x}\) в інтервальне позначення.
7) Дана\(f(x)=2 x^{2}-5 x,\) знахідка\(f(a+1)-f(1)\)
- Відповідь
-
\(2 a^{2}-a\)
8) Графік функції\(f(x)=\left\{\begin{array}{ccc}{x+1} & {\text { if }} & {-2<x<3} \\ {-x} & {\text { if }} & {x \geq 3}\end{array}\right.\)
9) Знайти середню швидкість зміни функції\(f(x)=3-2 x^{2}+x\) шляхом знаходження\(\dfrac{f(b)-f(a)}{b-a}\)
- Відповідь
-
\(-2(a+b)+1\)
Для вправ 10-11 використовуйте функції\(f(x)=3-2 x^{2}+x\) і\(g(x)=\sqrt{x}\) знайдіть складові функції.
10)\((g \circ f)(x)\)
11)\((g \circ f)(1)\)
- Відповідь
-
\(\sqrt{2}\)
12)\(H(x)=\sqrt[3]{5 x^{2}-3 x}\) Висловити склад з двох функцій,\(f\) і\(g,\) де\((f \circ g)(x)=H(x)\)
Для вправ 13-14 графуйте функції шляхом перекладу, розтягування та/або стиснення функції інструментарію.
13)\(f(x)=\sqrt{x+6}-1\)
- Відповідь
-
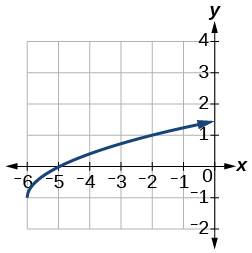
14)\(f(x)=\dfrac{1}{x+2}-1\)
Для вправ 15-17 визначте, чи є функції парними, непарними або ні.
15)\(f(x)=-\dfrac{5}{x^{2}}+9 x^{6}\)
- Відповідь
-
навіть
16)\(f(x)=-\dfrac{5}{x^{3}}+9 x^{5}\)
17)\(f(x)=\dfrac{1}{x}\)
- Відповідь
-
дивно
18) Графік функції абсолютного значення\(f(x)=-2|x-1|+3\).
19) Вирішити\(|2 x-3|=17\).
- Відповідь
-
\(x=-7\)і\(x=10\)
20) Вирішити\(-\left|\dfrac{1}{3} x-3\right| \geq 17\). Висловіть рішення в інтервальних позначеннях.
Для вправ 21-22 знайдіть зворотну функцію.
21)\(f(x)=3 x-5\)
- Відповідь
-
\(f^{-1}(x)=\dfrac{x+5}{3}\)
22)\(f(x)=\dfrac{4}{x+7}\)
Для вправ 23-26 скористайтеся графіком,\(g\) показаним на малюнку нижче.
23) На яких інтервалах збільшується функція?
- Відповідь
-
\((-\infty,-1.1)\)і\((1.1, \infty)\)
24) На яких інтервалах відбувається зменшення функції?
25) Приблизний локальний мінімум функції. Висловіть відповідь як впорядковану пару.
- Відповідь
-
\((1.1,-0.9)\)
26) Приблизний локальний максимум функції. Висловіть відповідь як впорядковану пару.
Для вправ 27-29 використовуйте графік кускової функції, показаний на малюнку нижче.
27) Знайти\(f(2)\).
- Відповідь
-
\(f(2)=2\)
28) Знайти\(f(-2)\).
29) Напишіть рівняння для кускової функції.
- Відповідь
-
\(f(x)=\left\{\begin{array}{cl}{|x|} & {\text { if } x \leq 2} \\ {3} & {\text { if } x>2}\end{array}\right.\)
Для вправ 30-35 використовуйте значення, наведені в таблиці нижче.
| \(x\) | \(F(x)\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 17 |
30) Знайти\(F(6)\).
31) Розв'яжіть рівняння\(F(x)=5\)
- Відповідь
-
\(x=2\)
32) Чи збільшується чи зменшується графік на своїй області?
33) Функція представлена графіком один до одного?
- Відповідь
-
так
34) Знайти\(F^{-1}(15)\).
35) Дана\(f(x)=-2 x+11,\) знахідка\(f^{-1}(x)\).
- Відповідь
-
\(f^{-1}(x)=-\dfrac{x-11}{2}\)
