1.7: Зворотні функції
- Page ID
- 61293
Цілі навчання
- Перевірте зворотні функції.
- Визначте область та діапазон оберненої функції та обмежте область функції, щоб зробити її один-на-один.
- Знайти або оцінити обернену функцію.
- Використовуйте графік функції один до одного для графіка її оберненої функції на однакових осях.
Реверсивний тепловий насос - це система клімат-контролю, яка являє собою кондиціонер і обігрівач в одному пристрої. Працюючи в одному напрямку, він відкачує тепло з будинку, щоб забезпечити охолодження. Працюючи в зворотному напрямку, він перекачує тепло в будівлю зовні, навіть в прохолодну погоду, для забезпечення обігріву. Як обігрівач тепловий насос в кілька разів ефективніше звичайного електричного опору опалення.
Якщо деякі фізичні машини можуть працювати в двох напрямках, ми можемо запитати, чи можуть деякі функції «машини», які ми вивчали, також можуть працювати назад. Малюнок\(\PageIndex{1}\) надає наочне уявлення про це питання. У цьому розділі ми розглянемо зворотний характер функцій.
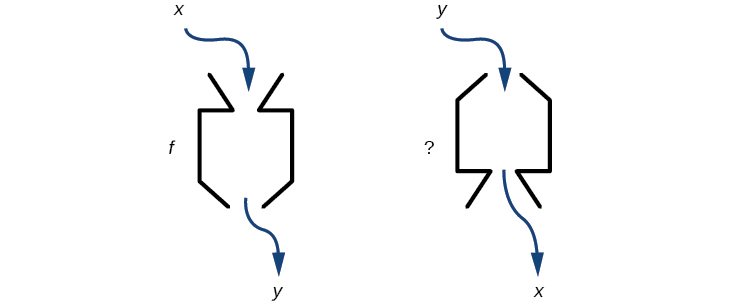
Малюнок\(\PageIndex{1}\): Чи може функція «машина» працювати в зворотному напрямку?
Перевірка того, що дві функції є оберненими функціями
Припустимо, модельєр, який їде в Мілан на показ мод, хоче знати, якою буде температура. Він не знайомий зі шкалою Цельсія. Щоб отримати уявлення про те, як пов'язані вимірювання температури, він просить свого помічника Бетті перетворити 75 градусів за Фаренгейтом в градуси Цельсія. Вона знаходить формулу
\[C=\dfrac{5}{9}(F−32)\]
і підставляє 75\(F\) для обчислення
\[\dfrac{5}{9}(75−32)\approx24^{\circ}\]
Знаючи, що комфортний 75 градусів за Фаренгейтом становить близько 24 градусів Цельсія, він надсилає своєму помічнику тижневий прогноз погоди з малюнка\(\PageIndex{2}\) для Мілана і просить її перетворити всі температури в градуси Фаренгейта.

Спочатку Бетті розглядає можливість використання формули, яку вона вже знайшла, щоб завершити перетворення. Адже вона знає свою алгебру, і може легко вирішити рівняння для\(F\) після підстановки значення для\(C\). Наприклад, щоб перетворити 26 градусів Цельсія, вона могла б написати
\[\begin{align} 26&=\dfrac{5}{9}(F-32) \\ 26⋅\dfrac{9}{5}&=F−32 \\ F&=26⋅\dfrac{9}{5}+32\approx79\end{align}\]
Однак, розглянувши цей варіант на мить, вона розуміє, що рішення рівняння для кожної з температур буде жахливо стомлюючим. Вона розуміє, що оскільки оцінка легше, ніж рішення, було б набагато зручніше мати іншу формулу, таку, яка приймає температуру за Цельсієм і виводить температуру Фаренгейта.
Формула, за якою шукає Бетті, відповідає ідеї зворотної функції, яка є функцією, для якої вхід вихідної функції стає виходом оберненої функції, а вихід вихідної функції стає входом оберненої функції.
Задано функцію\(f(x)\), ми представляємо її зворотну як\(f^{−1}(x)\), читається як «\(f\)обернена»\(x\). Піднятий −1 є частиною позначення. Він не є показником; він не означає ступінь −1. Іншими словами, це не\(f^{−1}(x)\) означає,\(\frac{1}{f(x)}\) тому що\(\frac{1}{f(x)}\) є взаємним,\(f\) а не зворотним.
Позначення «exponent-like» походить від аналогії між складом функцій і множенням: так само, як\(a^{−1}a=1\) (1 - елемент ідентичності для множення) для будь-якого ненульового числа\(a\), так\(f^{−1}{\circ}f\) дорівнює функції ідентичності, тобто
\[(f^{−1}{\circ}f)(x)=f^{−1}(f(x))=f^{−1}(y)=x\]
Це стосується всіх\(x\) у домені\(f\). Неофіційно це означає, що зворотні функції «скасовують» один одного. Однак так само, як нуль не має зворотного, деякі функції не мають зворотних.
Враховуючи функцію\(f(x)\), ми можемо перевірити, чи\(g(x)\) є інша функція зворотною,\(f(x)\) перевіривши, чи\(f(g(x))=x\) є\(g(f(x))=x\) або є істинним. Ми можемо перевірити будь-яке рівняння, з яким зручніше працювати, оскільки вони логічно еквівалентні (тобто якщо одне істинне, то інше так само).
Наприклад,\(y=4x\) і\(y=\frac{1}{4}x\) є зворотними функціями.
\[(f^{−1}{\circ}f)(x)=f^{-1}(4x)=\dfrac{1}{4}(4x)=x\]
і
\[(f{\circ}f^{−1})(x)=f\Big(\dfrac{1}{4}x\Big)=4\Big(\dfrac{1}{4}x\Big)=x\]
Кілька пар координат з графіка функції\(y=4x\) є\((−2, −8)\),\((0, 0)\), і\((2, 8)\). Кілька пар координат з графіка функції\(y=\frac{1}{4}x\) є\((−8, −2)\),\((0, 0)\), і\((8, 2)\). Якщо ми обміняємо вхідні та вихідні дані кожної пари координат функції, змінені пари координат з'являться на графіку оберненої функції.
Визначення: Обернена функція
Для будь-якої функції один до одного функція\(f(x)=y\)\(f^{−1}(x)\) є оберненою функцією\(f\) if\(f^{−1}(y)=x\). Це також може бути написано, як і\(f^{−1}(f(x))=x\) для всіх\(x\) в домені\(f\). Звідси також випливає, що\(f(f^{−1}(x))=x\) для всіх\(x\) в області\(f^{−1}\) if\(f^{−1}\) є зворотним\(f\).
Позначення\(f^{−1}\) читається «\(f\)зворотне». Як і будь-яка інша функція, ми можемо використовувати будь-яке ім'я змінної в якості вхідних даних для\(f^{−1}\), тому ми будемо часто писати\(f^{−1}(x)\), які ми читаємо як «\(f\)обернений»\(x\). Майте на увазі, що
\[f^{−1}(x)\neq\dfrac{1}{f(x)}\]
і не всі функції мають зворотні.
Приклад\(\PageIndex{1}\): Identifying an Inverse Function for a Given Input-Output Pair
Якщо для певної функції один до одного\(f(2)=4\) і\(f(5)=12\), які відповідні вхідні та вихідні значення для оберненої функції?
Рішення
Зворотна функція змінює вхідні та вихідні величини, так що якщо
\[f(2)=4, \text{ then } f^{-1}(4)=2 ;\\ f(5)=12, \text{ then }f^{-1}(12)=5\].
Крім того, якщо ми хочемо назвати зворотну функцію\(g\), то\(g(4)=2\) і\(g(12)=5\).
Аналіз
Зверніть увагу, що якщо ми покажемо пари координат у вигляді таблиці, вхідні та вихідні дані чітко змінюються. Див\(\PageIndex{1}\). Таблицю.
| \((x,f(x))\) | \((x,g(x))\) |
|---|---|
| \ (x, f (x))\)» style="вертикальне вирівнювання: по середині; вирівнювання тексту: по центру; ">\((2,4)\) | \ (x, g (x))\)» style="вертикальне вирівнювання: по середині; вирівнювання тексту: по центру; ">\((4,2)\) |
| \ (x, f (x))\)» style="вертикальне вирівнювання: по середині; вирівнювання тексту: по центру; ">\((5,12)\) | \ (x, g (x))\)» style="вертикальне вирівнювання: по середині; вирівнювання тексту: по центру; ">\((12,5)\) |
Вправа\(\PageIndex{1}\)
Враховуючи це\(h^{-1}(6)=2\), які відповідні вхідні та вихідні значення вихідної функції\(h\)?
- Відповідь
-
\(h(2)=6\)
Як: Враховуючи дві функції\(f(x)\) and \(g(x)\), test whether the functions are inverses of each other.
- Визначте,\(f(g(x))=x\) чи є чи\(g(f(x))=x\).
- Якщо обидва твердження вірні, то\(g=f^{-1}\) і\(f=g^{-1}\). Якщо будь-яке твердження є помилковим, то обидва є помилковими, і\(g{\neq}f^{-1}\) і\(f{\neq}g^{-1}\).
Приклад\(\PageIndex{2}\): Testing Inverse Relationships Algebraically
Якщо\(f(x)=\frac{1}{x+2}\) і\(g(x)=\frac{1}{x}−2\), є\(g=f^{-1}\)?
Рішення
\[\begin{align} g(f(x))&=\dfrac{1}{(\frac{1}{x+2})−2} \\ &=x+2−2 \\&=x \end{align}\]
тому
\[g=f^{-1} \text{ and } f=g^{-1}\]
Цього достатньо, щоб відповісти «так» на питання, але ми також можемо перевірити іншу формулу.
\[\begin{align} f(g(x))&=\dfrac{1}{\frac{1}{x}-2+2} \\ &= \dfrac{1}{\frac{1}{x}} \\ &=x \end{align}\]
Аналіз
Зверніть увагу, що зворотні операції знаходяться в зворотному порядку операцій від початкової функції.
Вправа\(\PageIndex{2}\)
Якщо\(f(x)=x^3−4\) і\(g(x)=\sqrt[3]{x+4}\), є\(g=f^{-1}\)?
- Відповідь
-
Так
Приклад\(\PageIndex{3}\): Determining Inverse Relationships for Power Functions
Якщо\(f(x)=x^3\) (функція куба) і\(g(x)=\frac{1}{3}x\), є\(g=f^{-1}\)?
Рішення
\[f(g(x))=\dfrac{x^3}{27}{\neq}x\]
Ні, функції не зворотні.
Аналіз
Правильний зворотний кубу - це, звичайно, кубічний корінь\(\sqrt[3]{x}=x^{\frac{1}{3}}\), тобто третина - показник, а не множник.
Вправа\(\PageIndex{3}\)
Якщо\(f(x)=(x−1)^3\) і\(g(x)=\sqrt[3]{x}+1\), є\(g=f^{-1}\)?
- Відповідь
-
Так
Пошук області та діапазону обернених функцій
Виходи функції\(f\) є входами до\(f^{-1}\), тому діапазон також\(f\) є областю\(f^{-1}\). Так само, оскільки входи\(f\) є виходами\(f^{-1}\), область\(f\) - це діапазон\(f^{-1}\). Ми можемо візуалізувати ситуацію, як на малюнку\(\PageIndex{3}\).
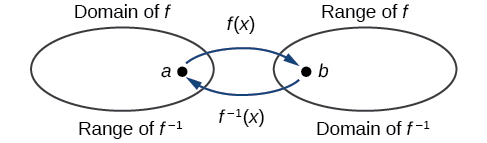
Рисунок\(\PageIndex{3}\): Домен та діапазон функції та її зворотна.
Коли функція не має зворотної функції, можна створити нову функцію, де ця нова функція в обмеженій області має обернену функцію. Наприклад, обернене\(f(x)=\sqrt{x}\) є\(f^{-1}(x)=x^2\), тому що квадрат «скасовує» квадратний корінь; але квадрат є лише зворотним квадратним коренем на області\(\left[0,\infty\right)\), оскільки це діапазон\(f(x)=\sqrt{x}\).
Ми можемо подивитися на цю проблему з іншого боку, починаючи з квадратної (квадратної) функції toolkit\(f(x)=x^2\). Якщо ми хочемо побудувати зворотну до цієї функції, ми стикаємося з задачею, тому що для кожного заданого виходу квадратичної функції є два відповідних входи (крім випадків, коли вхід дорівнює 0). Наприклад, вихід 9 з квадратичної функції відповідає входам 3 і —3. Але вихід з функції є входом до її зворотного; якщо цей зворотний вхід відповідає більш ніж одному оберненому виводу (вхід вихідної функції), то «обернений» взагалі не є функцією! Якщо говорити по-іншому, квадратична функція не є функцією один до одного; вона не проходить тест горизонтальної лінії, тому вона не має зворотної функції. Для того, щоб функція мала зворотну, вона повинна бути функцією один до одного.
У багатьох випадках, якщо функція не є один-на-один, ми все одно можемо обмежити функцію частиною її домену, на якій вона є один до одного. Наприклад, ми можемо зробити обмежену версію квадратної функції\(f(x)=x^2\) з обмеженою її діапазоном\(\left[0,\infty\right)\), яка є функцією один до одного (вона проходить тест горизонтальної лінії) і яка має зворотну (функція квадратного кореня).
Якщо\(f(x)=(x−1)^2\)\([1,∞)\) увімкнено, то обернена функція є\(f^{-1}(x)=\sqrt{x}+1\).
- Домен\(f\) = діапазон\(f^{-1} = \left[1,\infty\right)\).
- Домен\(f^{-1}\) = діапазон\(f = \left[0,\infty\right)\).
![]() Чи можливо, щоб функція мала більше одного оберненого?
Чи можливо, щоб функція мала більше одного оберненого?
Ні. Якщо дві нібито різні функції, скажімо,\(g\) і h, обидві відповідають визначенню бути зворотними іншої функції\(f\), то ви можете це довести\(g=h\). Ми щойно бачили, що деякі функції мають зворотні лише якщо ми обмежуємо домен оригінальної функції. У цих випадках може існувати кілька способів обмеження домену, що призводить до різних зворотних. Однак на якомусь одному домені оригінальна функція все ще має лише один унікальний зворотний.
Примітка: Домен і діапазон обернених функцій
Діапазон функції\(f(x)\) є областю оберненої функції\(f^{-1}(x)\).
Домен\(f(x)\) - це діапазон\(f^{-1}(x)\).
Як: Задано функцію, знайдіть область та діапазон її зворотного.
- Якщо функція один до одного, запишіть діапазон вихідної функції як область зворотної, а область вихідної функції запишіть як діапазон оберненої.
- Якщо область вихідної функції потрібно обмежити, щоб зробити її один-на-один, то цей обмежений домен стає діапазоном оберненої функції.
Приклад\(\PageIndex{4}\): Finding the Inverses of Toolkit Functions
Визначте, які з функцій інструментарію крім квадратичної функції не є один-на-один, і знайдіть обмежений домен, на якому кожна функція є один-на-один, якщо така є. Функції інструментарію розглянуті в табл\(\PageIndex{2}\). Обмежуємо домен таким чином, що функція приймає всі y-значення рівно один раз.
| Постійна | Ідентичність | Квадратичний | Кубічний | Взаємний |
|---|---|---|---|---|
| \(f(x)=c\) | \(f(x)=x\) | \(f(x)=x^2\) | \(f(x)=x^3\) | \(f(x)=\frac{1}{x}\) |
| Взаємний квадрат | Корінь куба | Квадратний корінь | Абсолютна величина | |
| \(f(x)=\frac{1}{x^2}\) | \(f(x)=\sqrt[3]{x}\) | \(f(x)=\sqrt{x}\) | \(f(x)=|x|\) |
Рішення
Постійна функція не є один-до-одному, і немає області (крім однієї точки), на якій вона могла б бути один-до-одному, тому постійна функція не має значущого зворотного.
Функція абсолютного значення може бути обмежена доменом\(\left[0,\infty\right)\), де вона дорівнює функції ідентичності.
Функція зворотного квадрата може бути обмежена доменом\((0,\infty)\).
Аналіз
Ми можемо побачити, що ці функції (якщо необмежені) не є один-на-один, дивлячись на їх графіки, показані на малюнку\(\PageIndex{4}\). Вони обидва не пройдуть тест на горизонтальну лінію. Однак, якщо функція обмежена певним доменом, щоб вона проходила тест горизонтальної лінії, то в цій обмеженій області вона може мати зворотний.
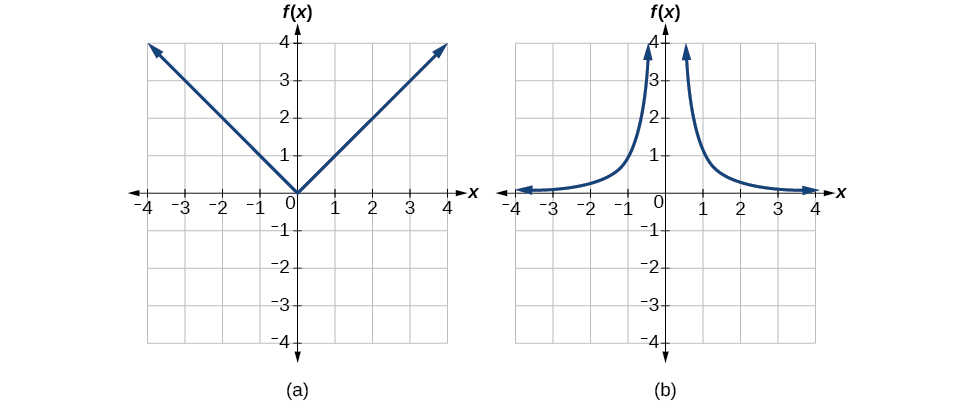
Рисунок\(\PageIndex{4}\): (a) Абсолютне значення (b) Зворотний квадрат
![]() \(\PageIndex{4}\): Домен функції\(f\) є\((1,\infty)\) і діапазон функції\(f\) є\((−\infty,−2)\). Знайти область і діапазон оберненої функції.
\(\PageIndex{4}\): Домен функції\(f\) є\((1,\infty)\) і діапазон функції\(f\) є\((−\infty,−2)\). Знайти область і діапазон оберненої функції.
Рішення
Домен функції\(f^{-1}\) є\((−\infty,−2)\) і діапазон функції\(f^{-1}\) є\((1,\infty)\).
Пошук та оцінка обернених функцій
Після того, як ми маємо функцію один-на-один, ми можемо оцінити її зворотну на конкретних зворотних входах функції або побудувати повне уявлення зворотної функції у багатьох випадках.
Інвертування табличних функцій
Припустимо, ми хочемо знайти обернену функцію, представлену в табличній формі. Пам'ятайте, що область функції - це діапазон зворотної, а діапазон функції - область зворотної. Таким чином, нам потрібно обмінюватися доменом і діапазоном.
Кожен рядок (або стовпець) входів стає рядком (або стовпцем) виходів для зворотної функції. Аналогічно, кожен рядок (або стовпець) виходів стає рядком (або стовпцем) входів для зворотної функції.
Приклад\(\PageIndex{5}\): Interpreting the Inverse of a Tabular Function
Функція\(f(t)\) наведена в таблиці\(\PageIndex{3}\), яка показує відстань у милі, яку автомобіль проїхав\(t\) за лічені хвилини. Знайти і інтерпретувати\(f^{-1}(70)\)
| \(t\)(хвилин) | 30 | 50 | 70 | 90 |
|---|---|---|---|---|
| \(f(t)\)(милі) | 20 | 40 | 60 | 70 |
Зворотна функція приймає вихід\(f\) і повертає вхідні дані для\(f\). Таким чином, у\(f^{-1}(70)\) виразі, 70 є вихідним значенням вихідної функції, що представляє 70 миль. Зворотний поверне відповідний вхід вихідної функції\(f\), 90 хвилин, так\(f^{-1}(70)=90\). Тлумачення цього полягає в тому, що, щоб проїхати 70 миль, знадобилося 90 хвилин.
Як варіант, нагадаємо, що визначення зворотного полягало в тому, що якщо\(f(a)=b\), то\(f^{-1}(b)=a\). За цим визначенням, якщо нам дано\(f^{-1}(70)=a\), то шукаємо значення\(a\) так, що\(f(a)=70\). В даному випадку ми шукаємо\(t\) так\(f(t)=70\), що, коли\(t=90\).
Вправа\(\PageIndex{5}\)
Використовуючи таблицю\(\PageIndex{4}\), знайдіть та інтерпретуйте (a)\(f(60)\) та (b)\(f^{-1}(60)\).
| \(t\)(хвилин) | 30 | 50 | 60 | 70 | 90 |
|---|---|---|---|---|---|
| \(f(t)\)(милі) | 20 | 40 | 50 | 60 | 70 |
- Відповідь
-
\(f(60)=50\). За 60 хвилин проїжджають 50 миль.
\(f^{-1}(60)=70\). Щоб проїхати 60 миль, знадобиться 70 хвилин.
Оцінка оберненої функції за заданим графіком початкової функції
У функціях та позначеннях функцій ми побачили, що область функції може бути прочитана, спостерігаючи горизонтальну протяжність її графіка. Домену оберненої функції ми знаходимо шляхом спостереження за вертикальною протяжністю графа початкової функції, оскільки це відповідає горизонтальній протяжності оберненої функції. Аналогічно, ми знаходимо діапазон оберненої функції, спостерігаючи горизонтальну протяжність графіка вихідної функції, оскільки це вертикальна протяжність оберненої функції. Якщо ми хочемо оцінити обернену функцію, ми знаходимо її вхід у межах її області, яка є всією або частиною вертикальної осі графіка вихідної функції.
![]() З огляду на графік функції, оцініть її зворотну в конкретних точках.
З огляду на графік функції, оцініть її зворотну в конкретних точках.
- Знайдіть потрібний вхід на осі y заданого графіка.
- Прочитайте вивід оберненої функції з осі x заданого графа.
Приклад\(\PageIndex{6}\): Evaluating a Function and Its Inverse from a Graph at Specific Points
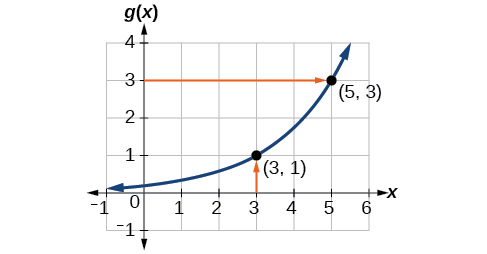
Функція\(g(x)\) наведена на рис\(\PageIndex{5}\). Знайти\(g(3)\) і\(g^{-1}(3)\).
.
Рішення
Для оцінки\(g(3)\) знаходимо 3 на осі x і знаходимо відповідне вихідне значення на осі y. Справа\((3,1)\) говорить нам про це\(g(3)=1\).
Щоб оцінити\(g^{-1}(3)\), нагадаємо, що під визначенням\(g^{-1}(3)\) означає значення\(x\) для якого\(g(x)=3\). Шукаючи вихідне значення 3 на вертикальній осі, знаходимо точку\((5,3)\) на графіку, що означає\(g(5)=3\), тому за визначенням\(g^{-1}(3)=5.\) див\(\PageIndex{6}\). Рис.
Вправа\(\PageIndex{6}\)
Використовуючи графік на малюнку\(\PageIndex{6}\), (а) знайдіть\(g^{-1}(1)\) і (б) оцініть\(g^{-1}(4)\).
- Відповідь на
-
3
- Відповідь б
-
5.6
Пошук обернень функцій, представлених формулами
Іноді нам потрібно знати зворотну функцію для всіх елементів своєї області, а не лише для кількох. Якщо вихідна функція задана у вигляді formula— наприклад,\(y\) як функція\(x\) - ми часто можемо знайти обернену функцію, вирішуючи отримати\(x\) як функцію\(y\).
Як: Задано функцію, представлену формулою, знайдіть обернену.
- Переконайтеся\(f\), що це функція один-на-один.
- Вирішити для\(x\)
- Розв'язка\(x\) і\(y\).
Приклад\(\PageIndex{7}\): Inverting the Fahrenheit-to-Celsius Function
Знайдіть формулу для оберненої функції, яка дає температуру Фаренгейта як функцію температури Цельсія.
\[C=\dfrac{5}{9}(F−32)\]
Рішення
\[\begin{align} C&=\frac{5}{9}(F-32) \\ C{\cdot}\frac{9}{5}&=F−32 \\ F&=\frac{9}{5}C+32\end{align}\]
Розв'язуючи загалом, ми розкрили обернену функцію. Якщо\[C=h(F)=\dfrac{5}{9}(F−32)\],
потім
\[F=h^{-1}(C)=\dfrac{9}{5}C+32.\]
У цьому випадку ми ввели функцію\(h\) для представлення перетворення, оскільки вхідні та вихідні змінні є описовими, і запис\(C^{-1}\) може заплутатися.
Вправа\(\PageIndex{7}\)
Вирішити для з\(x\) точки зору\(y\) заданого\(y=\frac{1}{3}(x−5)\)
- Відповідь
-
\(x=3y+5\)
Приклад\(\PageIndex{8}\): Solving to Find an Inverse Function
Знайдіть обернену функцію\(f(x)=\frac{2}{x−3}+4\).
Рішення
\[\begin{align} y&=\dfrac{2}{x−3+4} &\text{Set up an equation.} \\ y−4&=\dfrac{2}{x−3} &\text{Subtract 4 from both sides.} \\ x−3&=\dfrac{2}{y−4} &\text{Multiply both sides by x−3 and divide by y−4.} \\ x&=\dfrac{2}{y−4}+3 &\text{Add 3 to both sides.} \end{align}\]
Так\(f^{-1}(y)=\frac{2}{y−4}+3\) чи\(f^{-1}(x)=\frac{2}{x−4}+3\).
Аналіз
Домен і діапазон\(f\) виключають значення 3 і 4 відповідно. \(f\)і\(f^{-1}\) рівні в двох точках, але не є однаковою функцією, як ми можемо бачити, створивши таблицю\(\PageIndex{5}\).
| \(x\) | 1 | 2 | 5 | \(f^{-1}(y)\) |
|---|---|---|---|---|
| \(f(x)\) | 3 | 2 | 5 | \(y\) |
Приклад\(\PageIndex{9}\): Solving to Find an Inverse with Radicals
Знайдіть обернену функцію\(f(x)=2+\sqrt{x−4}\).
Рішення
\[ \begin{align} y&=2+\sqrt{x-4} \\ (y-2)^2&=x-4 \\ x&=(y-2)^2+4 \end{align}\]
Отже\(f^{-1}(x)=(x−2)^2+4\).
Домен\(f\) is\(\left[4,\infty\right)\). Зверніть увагу, що діапазон\(f\) є\(\left[2,\infty\right)\), так що це означає, що область\(f^{-1}\) зворотної функції також\(\left[2,\infty\right)\)
Аналіз
Формула, яку ми знайшли,\(f^{-1}(x)\) виглядає так, що вона була б дійсною для всіх реальних\(x\). Однак\(f^{-1}\) сам повинен мати зворотну (а саме\(f\)), тому ми повинні обмежити домен\(f^{-1}\) до,\(\left[2,\infty\right)\) щоб зробити\(f^{-1}\) функцію один до одного. Цей домен\(f^{-1}\) є саме діапазоном\(f\).
Вправа\(\PageIndex{8}\)
Що таке зворотна функція\(f(x)=2-\sqrt{x}\)? Створіть області як функції, так і зворотної функції.
- Відповідь
-
\(f^{-1}(x)=(2−x)^2\); домен\(f\):\(\left[0,\infty\right)\); домен\(f^{-1}\):\(\left(−\infty,2\right]\)
Пошук обернених функцій та їх графіків
Тепер, коли ми можемо знайти зворотну функцію, ми вивчимо графіки функцій та їх зворотні. Повернемося до квадратичної функції,\(f(x)=x^2\) обмеженої областю\(\left[0,\infty\right)\), на якій ця функція є один до одного, і графуємо її, як на рис\(\PageIndex{7}\).
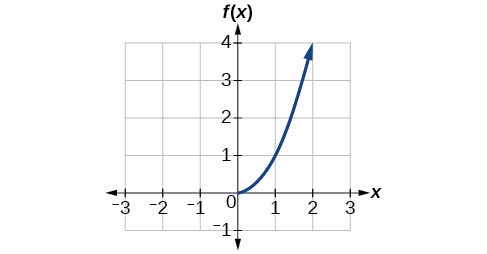
Малюнок\(\PageIndex{7}\): Квадратична функція з обмеженим доменом\([0, \infty)\).
Обмеження домену\(\left[0,\infty\right)\) робить функцію один-на-один (вона, очевидно, пройде тест горизонтальної лінії), тому вона має зворотну для цього обмеженого домену.
Ми вже знаємо, що оберненою квадратичною функцією інструментарію є функція квадратного кореня, тобто\(f^{-1}(x)=\sqrt{x}\). Що станеться, якщо ми графуємо обидва\(f\) і\(f^{-1}\) на одному наборі осей, використовуючи вісь x для входу обох\(f\) і\(f^{-1}\)?
Ми помічаємо чітке співвідношення: Графік\(f^{-1}(x)\) - це графік\(f(x)\) відбитих близько діагональної лінії\(y=x\), яку ми будемо називати лінією ідентичності, показаної на малюнку\(\PageIndex{8}\).
\ (f (x)\) і\(f^(-1)(x)\). "src=» https://math.libretexts.org/@api/dek..._01_07_009.jpg "/>.
Рисунок\(\PageIndex{8}\): Функції квадратного та квадратного кореня на невід'ємній області
Цей зв'язок буде спостерігатися для всіх функцій один до одного, оскільки це результат функції та її зворотної заміни входів і виходів. Це еквівалентно зміні ролей вертикальної і горизонтальної осей.
Приклад\(\PageIndex{10}\): Finding the Inverse of a Function Using Reflection about the Identity Line
З огляду на графік\(f(x)\) на малюнку\(\PageIndex{9}\), намалюйте графік\(f^{-1}(x)\).
Це функція один-на-один, тому ми зможемо накидати зворотну. Зверніть увагу, що показаний графік має видиму область\((0,\infty)\) і діапазон\((−\infty,\infty)\), тому зворотний буде мати область\((−\infty,\infty)\) і діапазон\((0,\infty)\).
Якщо відобразити цей графік над лінією\(y=x\), точка\((1,0)\) відображає до,\((0,1)\) а точка\((4,2)\) відображає до\((2,4)\). Ескіз оберненої на тих же осях, що і початковий графік, дає малюнок\(\PageIndex{10}\).
Вправа\(\PageIndex{1}\)
Намалюйте графіки функцій\(f\) і\(f^{-1}\) з Прикладу\(\PageIndex{8}\).
- Відповідь
-
\ (f (x)\) і\(f^(-1)(x)\).» src=» https://math.libretexts.org/@api/dek..._01_07_012.jpg "/>
Малюнок\(\PageIndex{11}\): Графік\(f(x)\) і\(f^(-1)(x)\).
![]() Чи існує якась функція, яка дорівнює власній оберненій?
Чи існує якась функція, яка дорівнює власній оберненій?
Так. Якщо\(f=f^{-1}\), то\(f(f(x))=x\), і можна придумати кілька функцій, які мають цю властивість. Функція ідентичності
робить, і так робить зворотна функція, тому що
\[\dfrac{1}{\frac{1}{x}}=x\]
Будь-яка функція\(f(x)=c−x\), де\(c\) знаходиться константа, також дорівнює власній оберненій.
Ключові концепції
- Якщо\(g(x)\) є зворотним\(f(x)\), то\(g(f(x))=f(g(x))=x\).
- Кожна з функцій інструментарію має зворотну.
- Щоб функція мала зворотну, вона повинна бути один-на-один (пройти тест горизонтальної лінії).
- Функція, яка не є один-на-один по всьому домену, може бути один-на-один на частину свого домену.
- Для табличної функції обмінюйте вхідні та вихідні рядки для отримання зворотного.
- Обернену функцію можна визначити в певних точках на її графіку.
- Щоб знайти зворотну формулу, розв'яжіть рівняння\(y=f(x)\) для\(x\) як функції\(y\). Потім обмінюємо етикетки\(x\) і\(y\).
- Графік оберненої функції є відображенням графіка вихідної функції по всій прямій\(y=x\).
