1.4: Склад функцій
- Page ID
- 61300
Цілі навчання
- Об'єднуйте функції за допомогою алгебраїчних операцій.
- Створіть нову функцію за складом функцій.
- Оцініть складові функції.
- Знайти область складеної функції.
- Розкласти складену функцію на її компонентні функції.
Припустимо, ми хочемо порахувати, скільки коштує обігрів будинку в конкретний день року. Вартість опалення будинку буде залежати від середньодобової температури, а в свою чергу, середньодобова температура залежить від конкретного дня року. Зверніть увагу, як ми тільки що визначили два співвідношення: Вартість залежить від температури, а температура залежить від дня.
Використовуючи описові змінні, ми можемо відзначити ці дві функції. Функція\(C(T)\) дає витрати на опалення будинку\(C\) при заданій середньодобовій температурі в\(T\) градусах Цельсія. Функція\(T(d)\) дає середньодобову температуру в день d року. Для будь-якого даного дня,\(Cost=C(T(d))\) означає, що вартість залежить від температури, яка в свою чергу залежить від дня року. Таким чином, ми можемо оцінити функцію витрат при температурі\(T(d)\). Наприклад, ми могли б оцінити,\(T(5)\) щоб визначити середньодобову температуру на 5-й день року. Тоді ми могли б оцінити функцію витрат при цій температурі. Ми б написали\(C(T(5))\).
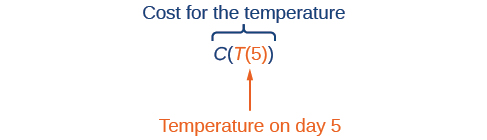
Об'єднавши ці дві зв'язки в одну функцію, ми виконали композицію функцій, яка є фокусом цього розділу.
Поєднання функцій за допомогою алгебраїчних операцій
Композиція функцій - це лише один із способів об'єднання існуючих функцій. Інший спосіб полягає в проведенні звичайних алгебраїчних операцій над функціями, такими як додавання, віднімання, множення і ділення. Ми робимо це, виконуючи операції з виходами функції, визначаючи результат як вихід нашої нової функції.
Припустимо, нам потрібно додати два стовпці цифр, які представляють окремі річні доходи чоловіка і дружини протягом періоду років, в результаті чого їх загальний дохід домогосподарства. Ми хочемо робити це за кожен рік, додаючи лише доходи цього року, а потім збираючи всі дані в нову графу. Якщо\(w(y)\) це дохід дружини і\(h(y)\) є доходом чоловіка в році\(y\), а ми\(T\) хочемо представляти загальний дохід, то можна визначити нову функцію.
\[T(y)=h(y)+w(y) \nonumber\]
Якщо це справедливо для кожного року, то ми можемо зосередитися на зв'язку між функціями без прив'язки до року і написати
\[T=h+w \nonumber\]
Так само, як для цієї суми двох функцій, ми можемо визначити різницю, добуток і співвідношення функцій для будь-якої пари функцій, які мають однакові типи входів (не обов'язково чисел), а також однакові види виходів (які повинні бути числами, щоб звичайні операції алгебри могли застосовуватися до них, і які також повинні мати однакові одиниці або без одиниць, коли ми додаємо і віднімаємо). Таким чином, ми можемо думати про додавання, віднімання, множення та ділення функцій.
Для двох функцій\(f(x)\) і\(g(x)\) з дійсним числом виходів ми визначаємо нові функції\(f+g\)\(f−g\),\(fg\),, і\(\frac{f}{g}\) по відносинам.
\[ \begin{align*} (f+g)(x) &=f(x)+g(x) \\[4pt] (f−g)(x) &=f(x)−g(x) \\[4pt] (fg)(x)&=f(x)g(x) \\[4pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)} \end{align*}\]
Приклад\(\PageIndex{1}\): Performing Algebraic Operations on Functions
Знайти і спростити функції\((g−f)(x)\) і\(\left(\dfrac{g}{f}\right)(x)\), задані\(f(x)=x−1\) і\(g(x)=x^2−1\). Вони однакові функції?
Рішення
Почніть з написання загальної форми, а потім підставляйте задані функції.
\[\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt] (g−f)(x) &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}\]
\[\begin{align*} \left(\dfrac{g}{f}\right)(x)&=g(x)f(x) \\[4pt] \left(\dfrac{g}{f}\right)(x)&=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1 \end{align*}\]
Ні, функції не однакові.
Примітка: Для\(\left(\dfrac{g}{f}\right)(x)\), умова\(x\neq1\) необхідна тому\(x=1\), що коли, знаменник дорівнює 0, що робить функцію невизначеною.
Вправа\(\PageIndex{1}\)
Знайти і спростити функції\((fg)(x)\) і\((f−g)(x)\).
\[f(x)=x−1 \nonumber\]
і
\[g(x)=x^2−1 \nonumber\]
Вони однакові функції?
- Відповідь
-
\((fg)(x)=f(x)g(x)=(x−1)(x2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2\)
Ні, функції не однакові.
Створення функції за складом функцій
Виконання алгебраїчних операцій над функціями об'єднує їх у нову функцію, але ми також можемо створювати функції, складаючи функції. Коли ми хотіли обчислити витрати на опалення з дня року, ми створили нову функцію, яка займає день як вхід і дає витрати як вихід. Процес об'єднання функцій так, що вихід однієї функції стає входом іншої відомий як склад функцій. Отримана функція відома як складова функція. Представляємо цю комбінацію наступними позначеннями:
\[f{\circ}g(x)=f(g(x))\]
Ми читаємо ліву частину як «\(f\)складається з\(g\) at»\(x\), а праву частину як «\(f\)\(g\)of»\(x\). дві сторони рівняння мають однакове математичне значення і рівні. Символ відкритого кола\(\circ\) називається оператором композиції. Ми використовуємо цей оператор головним чином, коли ми хочемо підкреслити зв'язок між самими функціями, не звертаючись до якогось конкретного вхідного значення. Композиція - це двійкова операція, яка приймає дві функції і утворює нову функцію, так само як додавання або множення приймає два числа і дає нове число. Однак важливо не плутати композицію функцій з множенням, оскільки, як ми дізналися вище, в більшості випадків\(f(g(x)){\neq}f(x)g(x)\).
Також важливо розуміти порядок операцій при оцінці складеної функції. Ми дотримуємося звичайної конвенції з дужками, починаючи спочатку з самих внутрішніх дужок, а потім працюючи назовні. У рівнянні вище функція\(g\) приймає вхід\(x\) першим і дає вихід\(g(x)\). Потім функція\(f\) приймає\(g(x)\) як вхід і видає вихід\(f(g(x))\).
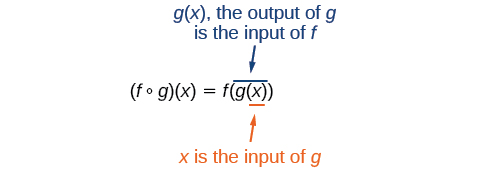
Загалом,\(f{\circ}g\) і\(g{\circ}f\) виконуються різні функції. Іншими словами, у багатьох випадках\(f(g(x)){\neq}g(f(x))\) для всіх\(x\). Ми також побачимо, що іноді дві функції можуть бути складені лише в одному певному порядку.
Наприклад, якщо\(f(x)=x^2\) і\(g(x)=x+2\), то
\[\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}\]
проте
\[\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}\]
Ці вирази не рівні для всіх значень x, тому дві функції не рівні. Неважливо, щоб вирази були рівними для одного вхідного значення\(x=−\frac{1}{2}\).
Зверніть увагу, що діапазон функції inside (перша функція, яку потрібно обчислити) повинен знаходитися в області зовнішньої функції. Менш формально склад повинен мати сенс з точки зору входів і виходів.
склад функцій
Коли вихід однієї функції використовується як вхід іншої, ми називаємо всю операцію складом функцій. Для будь-яких входів\(x\) і функцій\(f\) і\(g\), ця дія визначає складену функцію, яку ми пишемо як\(f{\circ}g\) таку, що
\[(f{\circ}g)(x)=f(g(x))\]
Домен складеної функції\(f{\circ}g\) - це все\(x\)\(x\) таке, що знаходиться в області\(g\) і\(g(x)\) знаходиться в області\(f\).
Важливо усвідомлювати, що добуток функцій не\(fg\) збігається з функціональним складом\(f(g(x))\), тому що, в цілому,\(f(x)g(x){\neq}f(g(x))\).
Приклад\(\PageIndex{2}\): Determining whether Composition of Functions is Commutative
Використовуючи надані функції, знайдіть\(f(g(x))\) і\(g(f(x))\). Визначте, чи є склад функцій комутативним.
\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]
Рішення
Давайте почнемо з підстановки\(g(x)\) в\(f(x)\).
\[\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}\]
Тепер ми можемо замінити\(f(x)\) в\(g(x)\).
\[\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}\]
Ми знаходимо\(g(f(x)){\neq}f(g(x))\), що, тому операція композиції функцій не є комутативною.
Приклад\(\PageIndex{3}\): Interpreting Composite Functions
Функція\(c(s)\) дає кількість спалених калорій, завершуючи\(s\) присідання, і\(s(t)\) дає кількість присідань, які людина може виконати за\(t\) лічені хвилини. Інтерпретувати\(c(s(3))\).
Рішення
Внутрішній вираз в композиції є\(s(3)\). Оскільки вхід до\(s\) -функції - це час,\(t=3\) представляє 3 хвилини, і\(s(3)\) це кількість присідань, виконаних за 3 хвилини.
Використання в\(s(3)\) якості входу в функцію\(c(s)\) дає нам кількість калорій, спалених під час кількості присідань, які можна виконати за 3 хвилини, або просто кількість калорій, спалених за 3 хвилини (роблячи присідання).
Приклад\(\PageIndex{4}\): Investigating the Order of Function Composition
Припустимо,\(f(x)\) дає милі, які можна\(x\) проїхати за годинами і\(g(y)\) дає галони газу, що використовується в проїзді\(y\) миль. Яке з цих виразів має сенс:\(f(g(y))\) або\(g(f(x))\)?
Рішення
Функція\(y=f(x)\) є функцією, виходом якої є кількість пройдених миль, що відповідає кількості пройдених годин.
\[\text{number of miles } =f (\text{number of hours}) \nonumber\]
Функція\(g(y)\) - це функція, виходом якої є кількість використаних галонів, що відповідає кількості пройдених миль. Це означає:
\[\text{number of gallons } =g(\text{number of miles}) \nonumber\]
Вираз\(g(y)\) приймає милі як вхідні дані, а кількість галонів - як вихід. Функція\(f(x)\) вимагає кілька годин в якості входу. Намагатися ввести кількість галонів не має сенсу. Вираз\(f(g(y))\) безглуздий.
Вираз\(f(x)\) займає години як вхідні дані, а кількість миль проїжджають як вихід. Функція\(g(y)\) вимагає кількості миль в якості вхідних даних. Використання\(f(x)\) (миль, керованих) в якості вхідного значення для\(g(y)\), де галони газу залежить від пробігу миль, має сенс. Вираз має\(g(f(x))\) сенс, і дасть кількість галонів використовуваного газу\(g\), проїжджаючи певну кількість миль\(f(x)\), в\(x\) годинами.
Питання/Відповідь
Чи є ситуації, коли\(f(g(y))\) і\(g(f(x))\) будуть обидва значущі або корисні вирази?
Так. Для багатьох чистих математичних функцій обидві композиції мають сенс, хоча вони зазвичай виробляють різні нові функції. У реальних задачах функції, входи та виходи яких мають однакові одиниці, також можуть давати композиції, які мають сенс у будь-якому порядку.
Вправа\(\PageIndex{2}\)
Гравітаційна сила на планеті на відстані\(r\) від сонця задається функцією\(G(r)\). Прискорення планети, що піддається будь-якій\(F\) силі, задається функцією\(a(F)\). Сформуйте осмислений склад цих двох функцій, і поясніть, що це означає.
- Відповідь
-
Гравітаційна сила все ще є силою, тому має\(a(G(r))\) сенс як прискорення планети на відстані\(r\) від Сонця (за рахунок гравітації), але\(G(a(F))\) не має сенсу.
Оцінка композитних функцій
Після того, як ми складемо нову функцію з двох існуючих функцій, ми повинні мати можливість оцінити її для будь-якого входу в її області. Ми зробимо це за допомогою конкретних числових входів для функцій, виражених у вигляді таблиць, графіків та формул, а також зі змінними як входами для функцій, виражених у вигляді формул. У кожному випадку ми оцінюємо внутрішню функцію, використовуючи початковий вхід, а потім використовуємо вихід внутрішньої функції як вхід для зовнішньої функції.
Оцінка складових функцій за допомогою таблиць
При роботі з функціями, заданими у вигляді таблиць, ми читаємо вхідні і вихідні значення з записів таблиці і завжди працюємо зсередини назовні. Спочатку ми оцінюємо функцію inside, а потім використовуємо вихід внутрішньої функції як вхід до зовнішньої функції.
Приклад\(\PageIndex{5}\): Using a Table to Evaluate a Composite Function
Використовуючи таблицю\(\PageIndex{1}\), оцініть\(f(g(3))\) і\(g(f(3))\).
| \(x\) | \(f(x)\) | \(g(x)\) |
|---|---|---|
| \ (x\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = "lt-math-1296">1 | \ (f (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">6 | \ (g (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">3 |
| \ (x\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = "lt-math-1296"> 2 | \ (f (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">8 | \ (g (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">5 |
| \ (x\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = "lt-math-1296">3 | \ (f (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">3 | \ (g (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296"> 2 |
| \ (x\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = "lt-math-1296">4 | \ (f (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">1 | \ (g (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">7 |
Рішення
Для оцінки\(f(g(3))\) починаємо зсередини з вхідного значення 3. Потім ми оцінюємо внутрішній вираз\(g(3)\) за допомогою таблиці, яка визначає функцію\(g: g(3)=2\). Потім ми можемо використовувати цей результат як вхід до функції\(f\), так\(g(3)\) замінюється на 2 і ми отримуємо\(f(2)\). Потім, використовуючи таблицю, яка визначає функцію\(f\), ми знаходимо, що\(f(2)=8\).
\[g(3)=2 \nonumber\]
\[f(g(3))=f(2)=8 \nonumber\]
Для оцінки\(g(f(3))\) спочатку оцінюємо внутрішній вираз,\(f(3)\) використовуючи першу таблицю:\(f(3)=3\). Потім, використовуючи таблицю для\(g\), ми можемо оцінити
\[g(f(3))=g(3)=2 \nonumber\]
Таблиця\(\PageIndex{2}\) показує складові функції\(f{\circ}g\) і\(g{\circ}f\) як таблиці.
| \(x\) | \(g(x)\) | \(f(g(x))\) | \(f(x)\) | \(g(f(x))\) |
|---|---|---|---|---|
| \ (x\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = "lt-math-1296">3 | \ (g (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296"> 2 | \ (f (g (x))\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">8 | \ (f (x)\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296">3 | \ (g (f (x))\)» style="вертикальне вирівнювання: середина; вирівнювання тексту: центр;» клас = «lt-math-1296"> 2 |
Вправа\(\PageIndex{3}\)
Використовуючи таблицю\(\PageIndex{1}\), оцініть\(f(g(1))\) і\(g(f(4))\).
- Відповідь
-
\(f(g(1))=f(3)=3\)і\(g(f(4))=g(1)=3\)
Оцінка складових функцій за допомогою графіків
Коли нам дають окремі функції у вигляді графіків, процедура оцінки складових функцій аналогічна процесу, який ми використовуємо для оцінки таблиць. Ми читаємо вхідні та вихідні значення, але на цей раз, з осей x та y графіків.
Як...
Задано складену функцію та графіки окремих її функцій, оцінюють її за допомогою інформації, наданої графіками.
- Знайдіть дані вхідні дані для внутрішньої функції на осі x її графіка.
- Зчитуйте висновок внутрішньої функції з осі y її графіка.
- Знайдіть вихід внутрішньої функції на осі x графіка зовнішньої функції.
- Прочитайте висновок зовнішньої функції з осі y її графіка. Це вихід складеної функції.
Приклад\(\PageIndex{6}\): Using a Graph to Evaluate a Composite Function
Використовуючи малюнок\(\PageIndex{3}\), оцінюємо\(f(g(1))\).
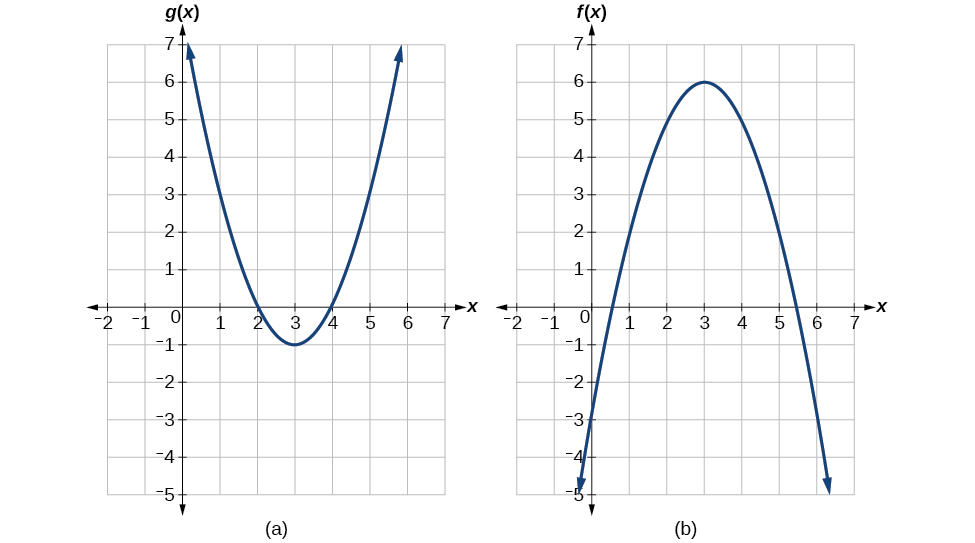
Рішення
Для оцінки\(f(g(1))\) ми починаємо з внутрішньої оцінки. Див\(\PageIndex{4}\). Малюнок.
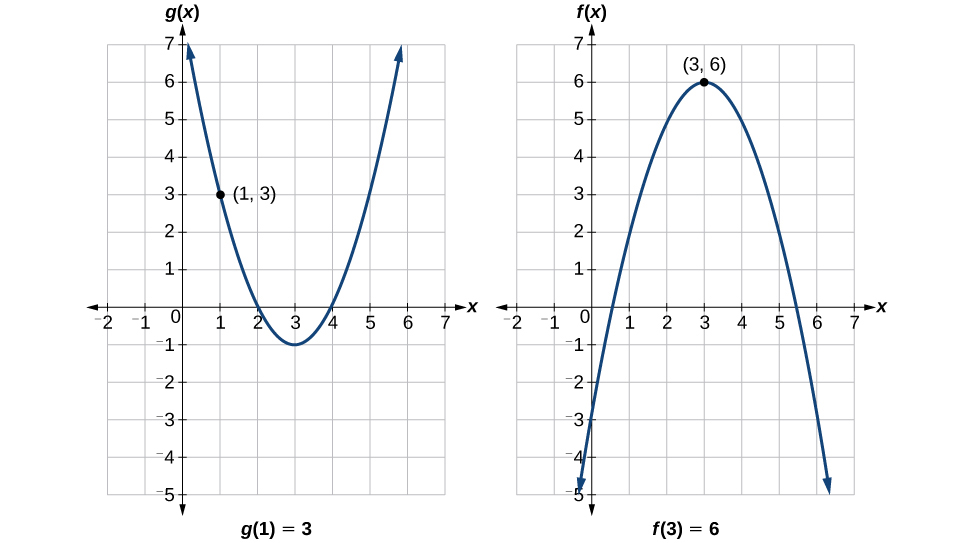
Ми оцінюємо\(g(1)\) за допомогою графіка\(g(x)\), знаходячи вхід 1 на осі x і знаходячи вихідне значення графіка на цьому вході. Ось,\(g(1)=3\). Ми використовуємо це значення як вхід у функцію\(f\).
\[f(g(1))=f(3) \nonumber\]
Потім ми можемо оцінити складену функцію, дивлячись на графік\(f(x)\), знаходячи вхід 3 на осі х і зчитуючи вихідне значення графіка на цьому вході. Ось\(f(3)=6\), так\(f(g(1))=6\).
Аналіз
На малюнку\(\PageIndex{5}\) показано, як ми можемо позначити графіки стрілками, щоб простежити шлях від вхідного значення до вихідного значення.
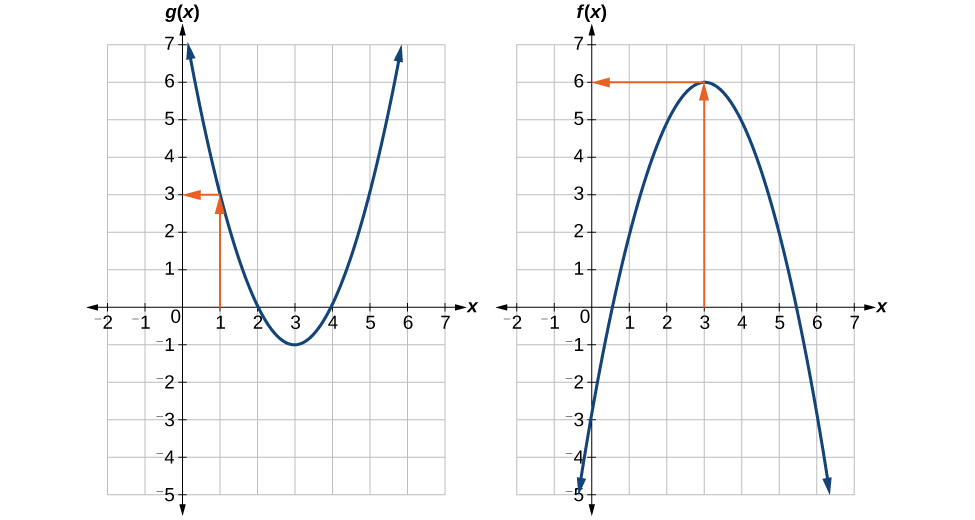
Вправа\(\PageIndex{4}\)
Використовуючи малюнок\(\PageIndex{3}\), оцінюємо\(g(f(2))\).
- Відповідь
-
\(g(f(2))=g(5)=3\)
Оцінка складових функцій за допомогою формул
При оцінці складеної функції, де ми або створили, або дали формули, правило роботи зсередини залишається тим самим. Вхідним значенням зовнішньої функції буде вихід внутрішньої функції, яка може бути числовим значенням, іменем змінної або більш складним виразом.
Хоча ми можемо скласти функції для кожного окремого вхідного значення, іноді корисно знайти єдину формулу, яка обчислить результат композиції\(f(g(x))\). Для цього ми розширимо нашу ідею оцінки функцій. Нагадаємо, що, коли ми оцінюємо функцію\(f(t)=t^2−t\), як, ми підставляємо значення всередині дужок у формулу всюди, де ми бачимо вхідну змінну.
Як...
Дано формулу для складеної функції, оцініть функцію.
- Оцініть внутрішню функцію, використовуючи вхідне значення або змінну, надану.
- Використовуйте отриманий висновок як вхід до зовнішньої функції.
Приклад\(\PageIndex{7}\): Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input
Дано\(f(t)=t^2−t\) і\(h(x)=3x+2\), оцініть\(f(h(1))\).
Рішення
Тому що всередині вираз\(h(1)\), ми починаємо з оцінки\(h(x)\) в 1.
\[ \begin{align*} h(1)=3(1)+2 \\[4pt] h(1)&=5 \end{align*} \]
Потім\(f(h(1))=f(5)\), таким чином, ми оцінюємо\(f(t)\) на вході 5.
\[ \begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*} \]
Аналіз
Немає різниці, що вхідні змінні\(t\) і\(x\) називалися в цій задачі, тому що ми оцінювали для конкретних числових значень.
Вправа\(\PageIndex{5}\)
З огляду\(f(t)=t^2−t\) і\(h(x)=3x+2\), оцініть
а.\(h(f(2))\)
б.\(h(f(−2))\)
- Відповідь на
-
8
- Відповідь б
-
20
Пошук області складеної функції
Як ми вже обговорювали раніше, область складеної функції, наприклад\(f{\circ}g\), залежить від області\(g\) та області\(f\). Важливо знати, коли ми можемо застосувати складову функцію, а коли ми не можемо, тобто знати область такої функції, як\(f{\circ}g\). Припустимо, ми знаємо області функцій\(f\) і\(g\) окремо. Якщо ми запишемо складену функцію для вхідних даних\(x\) як\(f(g(x))\), ми можемо відразу побачити, що\(x\) має бути членом області g для того, щоб вираз був значущим, тому що в іншому випадку ми не можемо завершити внутрішню оцінку функції. Однак ми також бачимо, що\(g(x)\) повинен бути членом області\(f\), інакше друга оцінка функції в\(f(g(x))\) не може бути завершена, а вираз все ще не визначено. Таким чином, область\(f{\circ}g\) складається тільки з тих входів в області\(g\), які виробляють виходи від\(g\) належності до області\(f\). Зауважте, що домен\(g\) composed with\(x\) - це набір усіх\(x\) таких, що знаходиться в області\(g\) і g (x)\) знаходиться в домені\(f\).\(f\)
Визначення: Домен складеної функції
Домен складеної функції\(f(g(x))\) - це сукупність тих входів\(x\) в області,\(g\) для яких\(g(x)\) знаходиться в області\(f\).
Як...
Задано функціональний склад\(f(g(x))\), визначте її область.
- Знайдіть домен домену\(g\).
- Знайдіть домен домену\(f\).
- Знайти ті\(x\) вхідні дані в області,\(g\) для яких\(g(x)\) знаходиться в домені\(f\). Тобто виключити ті вхідні\(x\) дані з домену\(g\) для яких не\(g(x)\) знаходиться в домені\(f\). Отриманий набір є доменом\(f{\circ}g\).
Приклад\(\PageIndex{8A}\): Finding the Domain of a Composite Function
Знайти домен
\[(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber\]
Рішення
Домен\(g(x)\) складається з усіх дійсних чисел\(x=\frac{2}{3}\), крім, оскільки це вхідне значення призведе до того, що ми ділимо на 0. Аналогічно, домен\(f\) складається з усіх дійсних чисел, крім 1. Таким чином, ми повинні виключити з домену\(g(x)\) того значення,\(x\) для якого\(g(x)=1\).
\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]
Таким чином, домен\(f{\circ}g\) являє собою набір всіх дійсних чисел, крім\(\frac{2}{3}\) і\(2\). Це означає, що
\[x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber\]
Ми можемо записати це в інтервалі позначення як
\[\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]
Приклад\(\PageIndex{8B}\): Finding the Domain of a Composite Function Involving Radicals
Знайти домен
\[(f{\circ}g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber\]
Рішення
Тому що ми не можемо взяти квадратний корінь від'ємного числа, домен\(g\) є\(\left(−\infty,3\right]\). Тепер перевіряємо домен складеної функції.
\[(f{\circ}g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber\]
Бо\((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\) так як радиканд квадратного кореня повинен бути позитивним. Так як квадратні корені є позитивними\(\sqrt{3−x}≥0\), або,\(3−x≥0,\) що дає домен\((-∞,3]\).
Аналіз
Цей приклад показує, що знання діапазону функцій (зокрема внутрішньої функції) також може бути корисним для пошуку області складеної функції. Він також показує, що домен\(f{\circ}g\) може містити значення, які не знаходяться в області\(f\), хоча вони повинні бути в області\(g\).
Вправа\(\PageIndex{6}\)
Знайти домен
\[(f{\circ}g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber\]
- Відповідь
-
\([−4,0)∪(0,∞)\)
Розкладання складеної функції на її компонентні функції
У деяких випадках необхідно розкласти складну функцію. Іншими словами, ми можемо записати його як композицію з двох простіших функцій. Існує кілька способів розкладання складеної функції, тому ми можемо вибрати розкладання, яке здається найбільш доцільним.
Приклад\(\PageIndex{9}\): Decomposing a Function
Напишіть\(f(x)=\sqrt{5−x^2}\) як склад двох функцій.
Рішення
Шукаємо дві функції,\(g\) і\(h\), так\(f(x)=g(h(x))\). Для цього шукаємо функцію всередині функції у формулі for\(f(x)\). Як одна з можливостей, ми можемо помітити, що вираз\(5−x^2\) є внутрішньою частиною квадратного кореня. Потім ми могли б розкласти функцію як
\[h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber\]
Ми можемо перевірити нашу відповідь, перекомпонувавши функції.
\[g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber\]
Вправа\(\PageIndex{7}\)
Напишіть\(f(x)=\dfrac{4}{3−\sqrt{4+x^2}}\) як склад двох функцій.
- Відповідь
-
Можливі відповіді:
\(g(x)=\sqrt{4+x^2}\)
\(h(x)=\dfrac{4}{3−x}\)
\(f=h{\circ}g\)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з складними функціями.
- Композитні функції (http://openstaxcollege.org/l/compfunction)
- Додаток для позначення композитних функцій (http://openstaxcollege.org/l/compfuncnot)
- Композитні функції з використанням графіків (http://openstaxcollege.org/l/compfuncgraph)
- Розкласти функції (http://openstaxcollege.org/l/decompfunction)
- Значення складових функцій (http://openstaxcollege.org/l/compfuncvalue)
Ключове рівняння
- Композитна функція\((f{\circ}g)(x)=f(g(x))\)
Ключові поняття
- Ми можемо виконувати алгебраїчні операції над функціями. Див. Приклад.
- При об'єднанні функцій вихід першої (внутрішньої) функції стає входом другої (зовнішньої) функції.
- Функція, що виробляється об'єднанням двох функцій, є складеною функцією. Див. Приклад і Приклад.
- Порядок композиції функцій необхідно враховувати при інтерпретації значення складових функцій. Див. Приклад.
- Складену функцію можна оцінити, оцінюючи внутрішню функцію за допомогою заданого вхідного значення, а потім оцінюючи зовнішню функцію, приймаючи за її вхід вихід внутрішньої функції.
- Складену функцію можна оцінити з таблиці. Див. Приклад.
- Складену функцію можна оцінити за графіком. Див. Приклад.
- Складену функцію можна оцінити за формулою. Див. Приклад.
- Домен складеної функції складається з тих входів в області внутрішньої функції, які відповідають виходам внутрішньої функції, які знаходяться в області зовнішньої функції. Див. Приклад і Приклад.
- Подібно до того, як функції можуть бути об'єднані для формування складеної функції, складові функції можуть бути розкладені на простіші функції.
- Функції часто можуть бути розкладені більш ніж одним способом. Див. Приклад.
Глосарій
- композитна функція
-
нова функція, утворена за складом функцій, коли вихід однієї функції використовується як вхід іншої
