Skip to main content
LibreTexts - Ukrayinska

8.4: Квадратичні послідовності

  1. Last updated
  2. Save as PDF
  • Page ID
    59550

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Квадратичні функції - це поліноміальні функції другого ступеня. Наприклад,\(f(x) = x^2\) являє собою квадратичну функцію. У цьому розділі будуть розглянуті закономірності в квадратичних функціях та послідовностях. Визначення шаблонів у таблиці функцій дає нам цінні підказки для побудови правильної функції, яка відповідає математичному шаблону.

    Як виявити квадратичну послідовність:

    На відміну від арифметичної послідовності, яка має загальну різницю\(d = a_n − a_{n-1}\), квадратична послідовність не матиме спільної різниці, поки не буде взята друга різниця, або різниця різниці!

    Розглянемо послідовність:\(1, 4, 9, 16, 25, …\) яка має загальний термін\(a_n = n^2\).

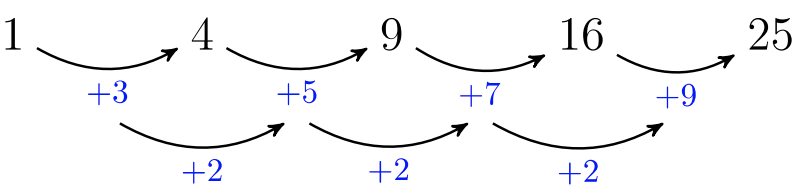
    clipboard_e10f4db8ad881b673244db0e5caf99a44.png

    Перша відмінність була взята, але спільної відмінності ми не знайшли. Перша відмінність дає незвичайні значення:\(3, 5, 7, 9\). Однак ми наполегливо і взяли різницю відмінностей:\(5 − 3 = 2\),\(7 − 5 = 2\), і\(9 − 7 = 2\). Другий шар відмінностей виявив спільне значення:\(2\). Послідовність є квадратичною послідовністю, якщо перша різниця не має спільної різниці, але друга відмінність робить!

    Послідовність квадратів - ще один красивий візуальний. Більше того, візуальне дійсно виправдовує, чому ми називаємо ці цифри «квадратами».

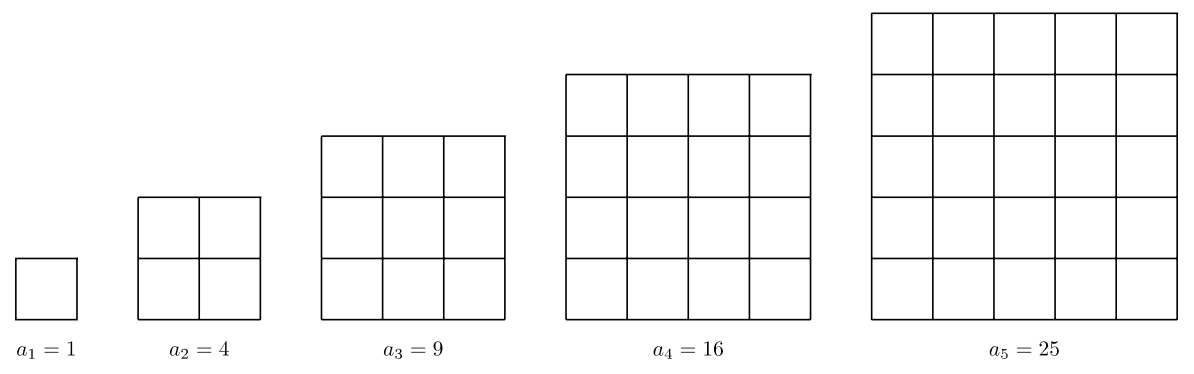
    clipboard_e93697812888fa20e1802dca89e35476a.png

    Примітно і те, що послідовність квадратів може створюватися послідовністю часткових сум непарних чисел. Диво математики продовжує нас дивувати!

    \(\begin{array} &a_1 &= 1 \\ a_2 &= 1 + 3 = 4 \\ a_3 &= 1 + 3 + 5 = 9\\ a_4 &= 1 + 3 + 5 + 7 = 16\\ a_5 &= 1 + 3 + 5 + 7 + 9 = 25 \\ \text{etc.} \end{array}\)

    Приклад Template:index

    Розглянемо викрійку нижче. Скільки маленьких квадратних плиток буде в\(10^{\text{th}}\) стадії\((a_{10})\) цього візерунка?

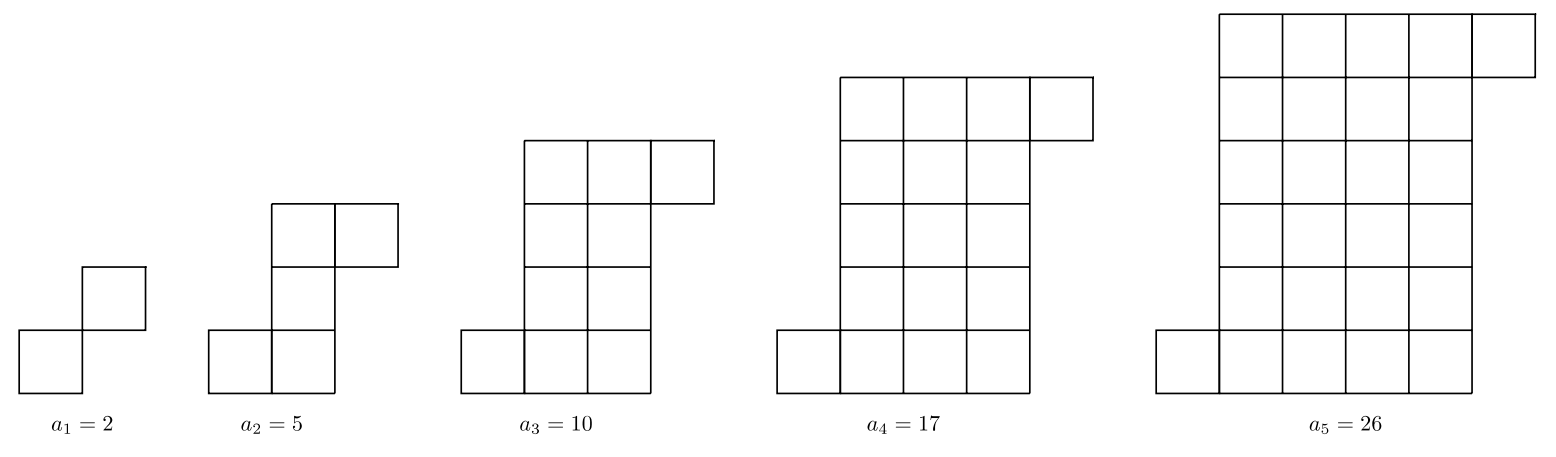
    clipboard_e21a3abd6fe152df245e014a981984c16.png

    Рішення

    Візерунок являє собою квадратичну послідовність:

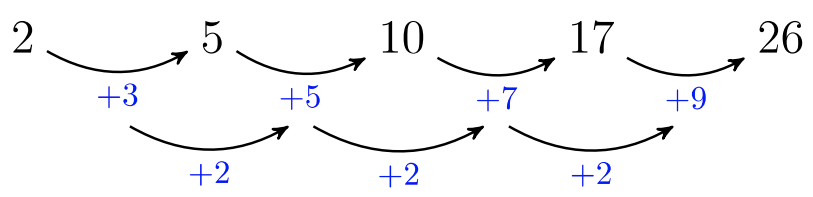
    clipboard_e05ac4753677f723394a7473851517c81.png

    Ми можемо переглянути\(2\) окремі шаблони. \(5^{\text{th}}\)Фігури\(2^{\text{nd}}\)\(3^{\text{rd}}\),\(4^{\text{th}}\), і містять візерунок квадратів:\(1, 4, 9, 16, …\) Нижче квадрати затінені жовтим кольором, що створює Візерунок квадратів. Верхній і нижній ряди створюють лінійний візерунок (синій), який представляє собою арифметичну послідовність.

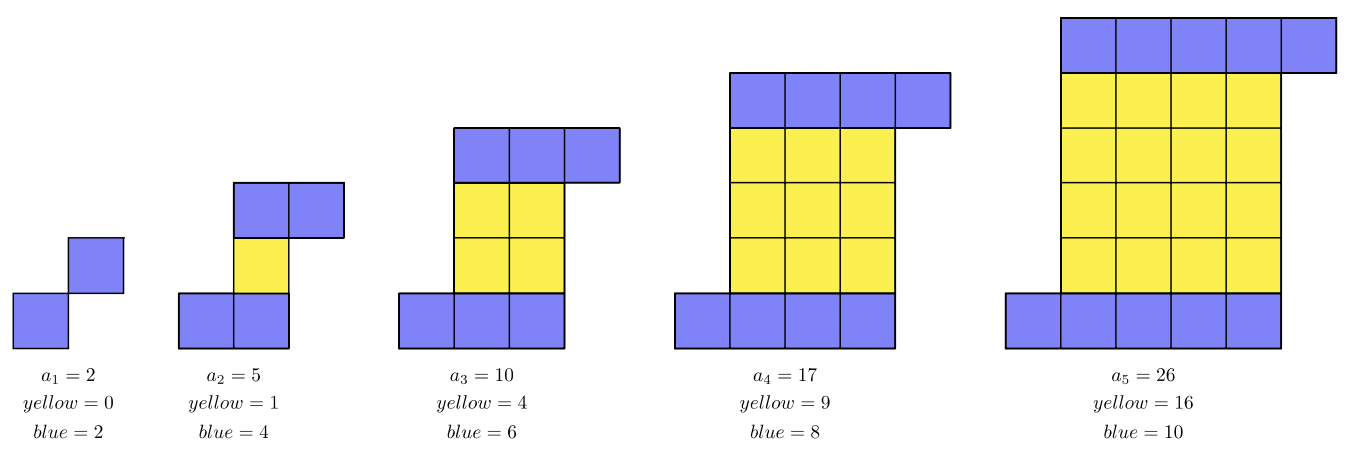
    clipboard_e9d0bbc2917ae3643c5be323ec9e848e0.png

    Синій послідовність - це те\(2, 4, 6, 8, 10, …\), що має загальний термін\(b_n = 2n\)

    Жовта послідовність - це те\(0, 1, 4, 9, 16, …\), що має загальний термін\(y_n = (n − 1)^2\)

    Синій і жовтий послідовність разом роблять загальну послідовність фігури,\(a_n\).

    \(\begin{array} &a_n &= b_n + y_n &\text{blue sequence \(+\)жовта послідовність\(= a_n\)}\\ a_n &= 2n + (n − 1) ^2 &\ text {Замініть загальний термін послідовності.}\\ a_n &=\ underbrace {2n} _ {\ текст {синій}} +\ підстроювання {n^2-2n+1} _ {\ text {жовтий}} &\ text {Розгорнути, використовуючи FOIL.}\\ a_n &n^2 + &\ текст {Спрощення.} \ end {масив}\)

    Приклад Template:index

    Перші\(4\) етапи викрійки показані нижче. Скільки кіл потрібно для побудови\(25^{\text{th}}\) сцени\((a_{25})\)?

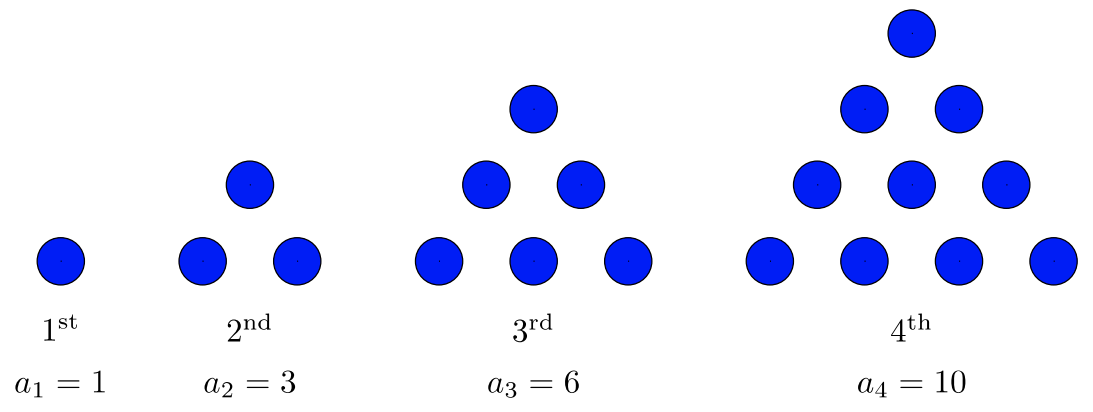
    clipboard_e4ae54cfeeffa20ee9084fa66a7da6bfd.png

    Рішення

    Кількість кіл на кожній фігурі створює квадратичну послідовність, яку ми можемо побачити, знайшовши загальну різницю у другій різниці.

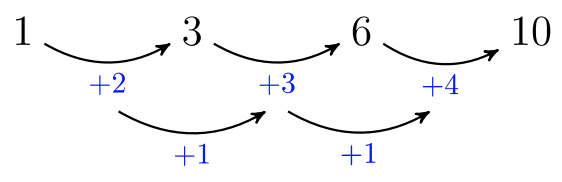
    clipboard_e6213b7767195bb57dc16e6fc190ac83c.png

    Завдання тут полягає в тому, щоб знайти значення\((a_{25})\). Хоча є багато підходів, які можна було б прийняти, це один із способів знайти\((a_{25})\).

    Зверніть увагу, що послідовність\(1, 3, 6, 10, …\) є послідовністю часткових сум послідовних чисел:

    Тому,\(a_{25} = 1 + 2 + 3 + ⋯ + 25\). Замість того, щоб виконувати додавання по одному члену за раз, давайте запишемо суму двічі: одне збільшення, а одне зменшення, потім додаємо вертикально. Відбувається класна річ:

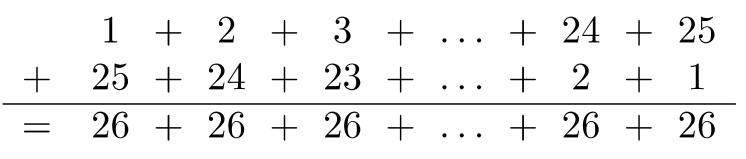
    clipboard_e9460b09125c0deee5cfcca9a452ac288.png

    Тому,

    \(\begin{array} &a_{25} + a_{25} &= 25 \cdot 26 \\ 2a_{25} &= 650 \\ \dfrac{2a_{25}}{2} &= \dfrac{650}{2} \\ a_{25} &= 325 \end{array}\)

    Додавання послідовних чисел: від 1 до n:

    У попередньому прикладі (приклад 8.4.2) був продемонстрований метод знаходження суми перших\(25\) послідовних чисел.

    \(1 + 2 + 3 + ⋯ + 25 = \dfrac{25 \cdot 26}{2}\)

    Узагальнимо знахідку\(s_n\), суму перших\(n\) послідовних натуральних чисел. Знову ж таки, використовуючи метод Example\(8.4.2\):

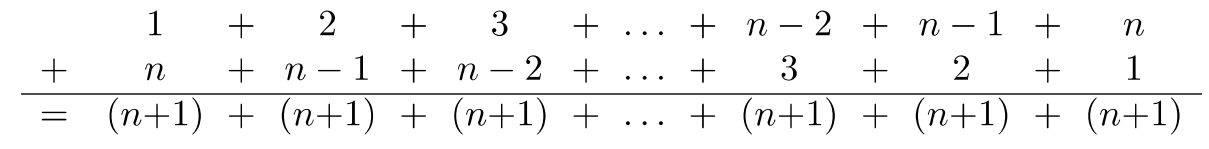
    clipboard_e7018fea7e73a8a8cead911c1d1616c3b.png

    Тому,

    \(\begin{array} & s_n + s_n &= n(n + 1) \\ 2s_n &= n(n + 1) \\ \dfrac{2s_n}{2} &= \dfrac{n(n + 1)}{2} \\ s_n &= \dfrac{n(n + 1)}{2} \end{array}\)

    Приклад Template:index

    У свій перший день заняття вчитель Джексона просить учня потиснути руку і представитися один одному. У класі є\(25\) учні. Скільки різних рукостискань може статися під час цього криголама, якщо кожен студент потисне руку кожному іншому учню?

    Рішення

    Важливим кроком до вирішення проблеми є розуміння проблеми. Почнемо з малого. Припустимо, що в класі є тільки\(2\) люди. Якщо Хлоя потисне руку Джексону, сталося одне рукостискання, і все! Тепер давайте додамо ще одну людину в кімнату і розглянемо клас\(3\) учнів. Потім додайте ще один для розміру класу\(4\). Потім ще... і створіть діаграму результатів.

    \(n =\)розмір класу \(b_n =\)рукостискання
    \ (n =\) розмір класу">\(2\) \ (b_n =\) рукостискання">\(1\)
    \ (n =\) розмір класу">\(3\) \ (b_n =\) рукостискання">\(3\)
    \ (n =\) розмір класу">\(4\) \ (b_n =\) рукостискання">\(6\)
    \ (n =\) розмір класу">\(5\) \ (b_n =\) рукостискання">\(10\)

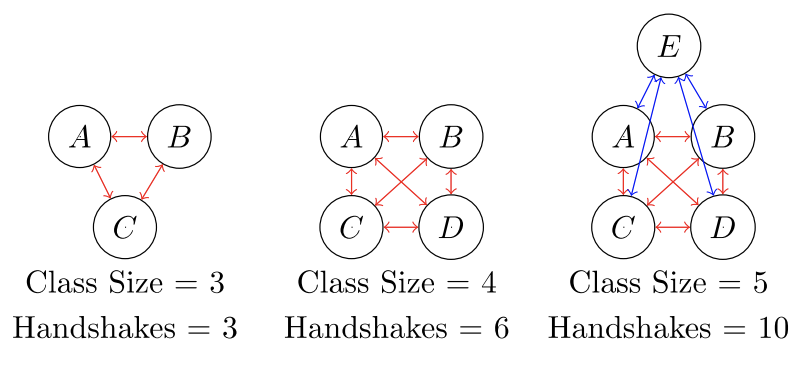
    clipboard_e4564a6e2c5f0912035055e15b5bab059.png

    Візерунок з'являється так само, як у попередньому прикладі (приклад 8.4.2). Однак\(n\) -значення (розмір класу) на один більше, ніж\(n\) -values (номер малюнка) у прикладі 8.4.2. Ми можемо легко підлаштуватися під різницю. Порівняйте таблиці між двома прикладами та відповідним чином відрегулюйте

    З прикладу\(8.4.2\)
    \ (8.4.2\) "> номер\(n =\) малюнка \(a_n =\)Кількість кіл
    \ (8.4.2\) ">\(1\) \(1\)
    \ (8.4.2\) ">\(2\) \(3\)
    \ (8.4.2\) ">\(3\) \(6\)
    \ (8.4.2\) ">\(4\) \(10\)
    \ (8.4.2\) ">\(n\) \(\dfrac{n(n+1)}{2}\)

    Використовуйте приклад 8.4.2 як модель для пошуку формули для Прикладу 8.4.3. The\(n\)-values of Example 8.4.2 are one less than the \(n\)-values of Example 8.4.3.

    З прикладу\(8.4.3\)
    \ (8.4.3\) "> розмір\(n =\) класу \(b_n =\)рукостискання
    \ (8.4.3\) ">\(2\) \(1\)
    \ (8.4.3\) ">\(3\) \(3\)
    \ (8.4.3\) ">\(4\) \(6\)
    \ (8.4.3\) ">\(5\) \(10\)
    \ (8.4.3\) ">\(n\) Формула?

    Оскільки ми знаємо формулу для Прикладу 8.4.2, давайте скоригуємо\(n\) −значення Прикладу відповідно\(8.4.3\) до Прикладу 8.4.2. Оскільки ми зіставляємо приклад 8.4.3 до прикладу 8.4.2, нам потрібно відняти один з\(n\) -значення. По суті,\(b_n\) значення Прикладу 8.4.3 (рукостискання) відповідає значенню\(a_{n-1}\) наприклад 8.4.2 (кількість кіл).

    \(b_{25}\)Приклад 8.4.3 такий же, як\(a_{24}\) у прикладі 8.4.2.

    Важливим навиком для вирішення проблем є використання роботи, яка вже досягнута. Не кожна проблема - свіжий шифер.

    \(\begin{array}& a_{24} &= \dfrac{24(24+1)}{2} &\text{Substitute \(n = 24\)у формулі Приклад 8.4.2.}\\ a_ {24} &=\ dfrac {24 (25)} {2} &\ text {Спростіть дужки.}\\ a_ {24} &=\ dfrac {600} {2} &\ text {Спрощення чисельника. Потім розділіть.}\\ a_ {24} &= 300 &\ text {Але тепер застосуйте цю відповідь до Прикладу 8.4.3:\(b_{25} = 300\).} \ end {масив}\)

    Щоб знайти формулу\(a_n\), наприклад 8.4.3, замініть\((n − 1)\)\(n\) в прикладі 8.4.2.

    Формула для прикладу 8.4.3:

    \(\begin{array} && \dfrac{(\textcolor{red}{n−1})[(\textcolor{red}{n−1})+1]}{2} &\text{Replace each \(n\)з\((n − 1)\) у формулі Прикладу 8.4.2.}\\ &\ dfrac {(n−1) n} {2} &\ text {Спрощення в дужках.}\\ &\ dfrac {n (n−1)} {2} &\ text {Це формула для прикладу 8.4.3.}\ &b_ {25} =\ dfrac {25 (24)} {2}\\\ & text {Переконайтеся, що ми отримали таку ж відповідь\(300\), як і вище.}\ \ &b_ {25} = 300 &\ end {масив}\)

    Відповідь У класі\(25\) студентів Ієроніма були б\(300\) різні рукостискання, якби кожен студент потиснув руку кожному іншому учню.

    Спробуйте! (Вправи)

    Для #1 -3 задано загальний термін послідовності.

    а. вкажіть перші п'ять термінів, починаючи з\(n = 1\).

    b. знайти значення\(a_{12}\).

    1. \(a_n = n^2 + n − 1\)
    2. \(a_n = 2(n + 1) 2\)
    3. \(a_n = 2n^2 + 2\)

    Для #4 -8, Нехай\(s_n =\) сума перших\(n\) послідовних натуральних чисел. Знайдіть вказане значення.

    1. \(s_{32}\)
    2. \(s_{80}\)
    3. \(s_{100}\)
    4. \(s_{201}\)
    5. \(s_{496}\)

    Для #9 -13, У кімнаті є\(n\) люди, всі з яких будуть один раз потиснути руку кожному іншому в кімнаті. Нехай\(b_n =\) кількість різних рукостискань. Знайдіть вказане значення.

    1. \(b_{16}\)
    2. \(b_{36}\)
    3. \(b_{52}\)
    4. \(b_{100}\)
    5. \(b_{229}\)
    6. Знайти суму перших\(30\) непарних чисел.
    7. Використовуйте той факт, що\(2 + 4 + 6 + 8 + ⋯ = 2(1 + 2 + 3 + 4 + ⋯ )\) для знаходження суми перших\(50\) парних чисел.
    8. Напишіть формулу для опису суми першого\(n\) числа парних чисел.

    Для #17 -21, Візерунок фігур показаний нижче. Нехай\(a_n =\) кількість невеликих квадратних плиток використовується для створення малюнка\(n\). Знайдіть вказане значення.

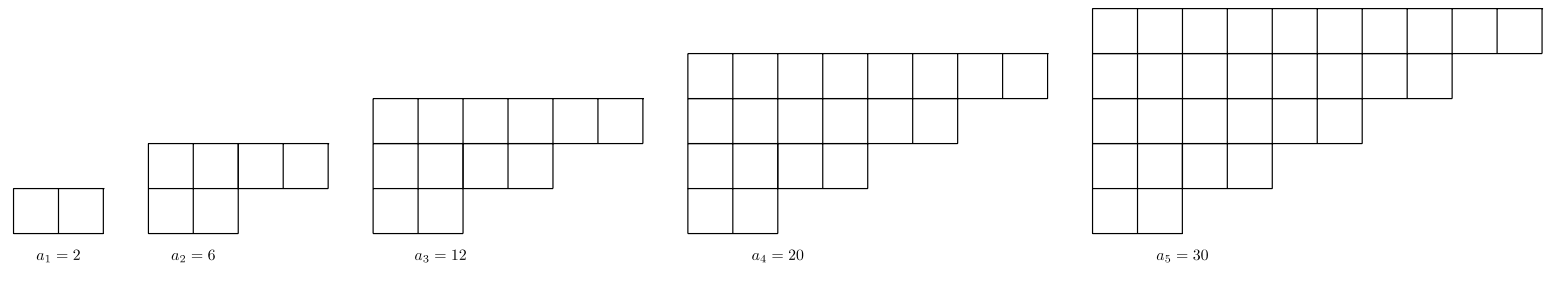
    clipboard_ec28104a668a2c53146a30feee403d95d.png

    1. \(a_{6}\)
    2. \(a_{8}\)
    3. \(a_{22}\)
    4. \(a_{60}\)
    5. Формула\(a_n\).

    Для #22 -24 спочатку визначте кількість сірників на кожному малюнку 1-4. Нехай\(a_n =\) кількість сірників на малюнку\(n\). Знайдіть вказане значення.

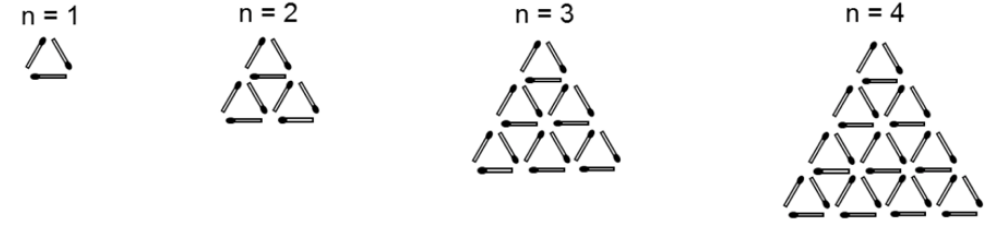
    clipboard_ee9c10f82919a4bb25777d617860c0615.png

    1. \(a_5\)
    2. Знайти,\(a_n\) враховуючи, що\(a_n = \dfrac{3n(n+k)}{2}\) для деяких\(k\).
    3. \(a_{45}\)

    Для #25 -27\(4\) багатокутники нижче демонструють, як рахувати діагоналі всередині кожного багатокутника. Діагональ (показана синім кольором) - це з'єднання несусідніх вершин. Нехай\(p_n =\) кількість діагоналей у будь-якій\(n\) −бічній фігурі. Знайдіть вказане значення.

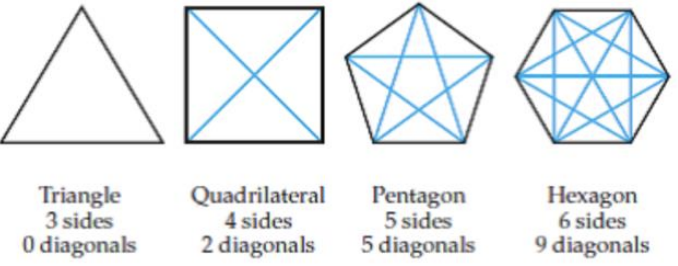
    clipboard_e32128b40b8cb3908f1c93e61ec0747aa.png

    1. \(p_7\)
    2. З огляду на, що\(p_n = \dfrac{n(n−k)}{2}\) для деяких\(k\), знайти\(k\) і\(p_n\).
    3. \(p_{40}\)

    Для #28 -30 зверніться до експерименту з гравітацією, описаним нижче:

    Вам цікаво, чи існує взаємозв'язок між кількістю футів, які м'яч падає з балконних\(144\) футів над землею. Ви налаштували камеру для фотографування щосекунди, коли куля падає перед діаграмою висоти. Ви створюєте наступну таблицю на основі фотографій:

    Час (сек) \(0\) \(1\) \(2\) \(3\)
    Відстань (фути) \(0\) \(16\) \(64\) \(144\)
    1. Ви міркуєте, що відстань м'яча є квадратичною послідовністю. Звідки ти знав?
    2. Після побудови графіків точок, ви вважаєте, що послідовність має загальний термін,\(d_t = kt^2\) де\(t =\) час у секундах і\(k\) є дійсним числом. Визначте значення\(k\), потім знайдіть\(d_t\).
    3. Використовуючи свої відповіді на #28 і #29, припустимо, що ви стояли на вершині скелі, для якої ви не знали висоти. Ви впустили скелю з вершини. \(6\)Через кілька секунд ви почули, як скеля вдарилася об землю. Наскільки високо ти над землею?

    Для #31 -33 використовуйте таблицю для опису підйому літаків:

    Для заданої площі крила підйом літака пропорційний квадрату його швидкості.

    Нехай\(s =\) швидкість літака. Тоді\(l_s = ks^2\) для якоїсь постійної,\(k\).

    У таблиці нижче показаний підйомник для літака Boeing 737 на різних швидкостях.

    Швидкість (миль/год) \(0\) \(75\) \(150\) \(225\) \(300\) \(375\)
    Ліфт (\(1000\)фунти) \(0\) \(25\) \(100\) \(225\) \(400\) \(625\)
    1. Ви міркуєте, що підйом літака є квадратичною послідовністю. Звідки ти знав?
    2. Після графіка точок, ви вважаєте, що послідовність має загальний термін,\(l_s = ks^2\) де\(s =\) швидкість в миль/год і\(k\) є постійною. Визначте значення\(k\), потім знайдіть\(l_s\).
    3. Використовуйте свої відповіді на #31 і #32, щоб знайти ліфт для літака, який подорожує\(425\) миль/год.