Skip to main content
LibreTexts - Ukrayinska

6.1: Спрощення радикальних виразів

  1. Last updated
  2. Save as PDF
  • Page ID
    59497

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Хто не любить команду «скасувати» на комп'ютері? Радикали схожі на команду скасування всіх повноважень. Якщо прийняття повноважень - це пряма дія, то радикали вимагають від нас думати назад. Щоб підготуватися до цього розділу, запам'ятайте перші дванадцять ідеальних квадратів і перші п'ять кубиків. Буде дуже корисно визнати повноваження\(2\) і\(3\).

    Визначення: Ідеальні квадрати та ідеальні кубики для запам'ятовування

    Ідеальні квадрати для запам'ятовування (перші дванадцять):

    \(1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, …\)

    Кубики для запам'ятовування (перші п'ять):

    \(1, 8, 27, 64, 125, …\)

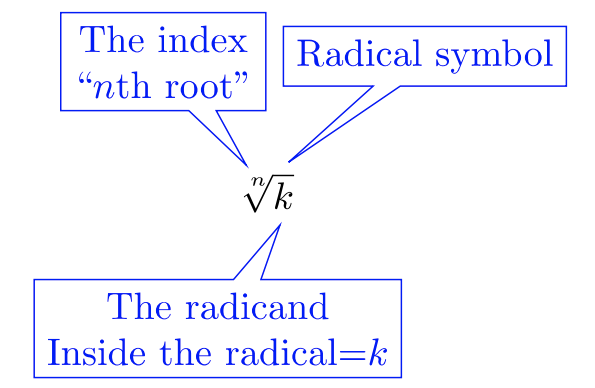
    Давайте розглянемо анатомію радикала:

    clipboard_eaecd674719fbdb4cc9fbd5ec372189d8.png

    Індекс\(n\) Приклад Читати вголос
    \ (n\) ">Типовий індекс\(n=2\) \(\sqrt{4}\) Квадратний корінь з\(4\).
    \ (n\) ">\(n=3\) \(\sqrt[3]{8}\) Кубик корінь з\(8\).
    \ (n\) ">\(n=4\) \(\sqrt[4]{16}\) \(4^{\text{th}}\)Корінь з\(16\).
    \ (n\) ">\(n=5\) \(\sqrt[5]{32}\) \(5^{\text{th}}\)Корінь з\(32\).

    Індекс,\(n\), вказує на показник спорідненої влади.

    \(\begin{array} &\sqrt{4} &= 2 &\text{Why? Because \(2^2 = 4\).}\\ sqrt [3] {8} &= 2 &\ text {Чому? Тому що\(2^3 = 8\).}\\ sqrt [4] {16} &= 2 &\ text {Чому? Тому що\(2^4 = 16\).}\\ sqrt [5] {32} &= 2 &\ text {Чому? Тому що\(2^5 = 32\).} \ end {масив}\)

    Всі чотири приклади вище мають значення\(2\).

    Приклад Template:index

    Спростити.

    1. \(\sqrt{\dfrac{9}{64}}\)
    2. \(\sqrt[3]{−64}\)
    3. \(\sqrt{−81}\)
    4. \(\sqrt[5]{100000}\)

    Рішення

    1. \(\begin{array} & \sqrt{\dfrac{9}{64}} = \dfrac{3}{8} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{\(\sqrt{\dfrac{9}{64}} = \dfrac{3}{8}\)тому що\(\dfrac{3}{8} ≥ 0\) і\(\left( \dfrac{3}{8} \right)^2 = \dfrac{9}{64}\).} \ end {масив}\)
    2. \(\begin{array} & \sqrt[3]{−64} = −4 &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{\(\sqrt[3]{−64} = −4\)тому що\(n = 3\) є непарним і\((−4)^3 = −64\).} \ end {масив}\)
    3. \(\begin{array} & \sqrt{−81} \text{ is not a real number.} &\;\;\;\;\;\;\;\;\;\;\text{No real number, when squared, equals \(−81\).} \ end {масив}\)
    4. \(\begin{array} & \sqrt[5]{100000} = 10 &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{\(\sqrt[5]{100000} = 10\)тому що\(10^5 = 100000\).} \ end {масив}\)

    Властивості та приклади (нижче) будуть включати радиканд зі змінними. З цього моменту ми будемо вважати, що всі змінні навіть індексованих радикалів є невід'ємними значеннями. Тобто, для\(\sqrt[n]{x^p}\) і\(n\) є парним, будемо вважати\(x ≥ 0\).

    Нерухомість Приклади
    1. \(\sqrt[n]{a^n} = a\) \(\sqrt[4]{x^4} = x\)або\(\sqrt[3]{(-5)^3} = -5\)
    2. Властивість продукту:\(\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab}\) \(\sqrt[5]{6} \cdot \sqrt[5]{x^2} = \sqrt[5]{6x^2}\)або\(\sqrt{100x^4} = \sqrt{100} \cdot \sqrt{x^4} = 10x^2\)
    3. Частота власності:\(\sqrt[n]{\dfrac{a}{b}} = \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) \(\sqrt{\dfrac{x^2}{100}} = \dfrac{\sqrt{x^2}}{\sqrt{100}} = \dfrac{x}{10}\)або\(\dfrac{\sqrt[3]{54}}{\sqrt[3]{16}} = \sqrt[3]{\dfrac{54}{16}} = \sqrt[3]{\dfrac{27}{8}} = \dfrac{3}{2}\)
    Визначення

    \(n\)Дозволяти\(m\) і бути цілими числами, такими, що\(m/n\) є раціональним числом в найнижчих числах і\(n > 1\). Потім,

    \(a^{1/n} = \sqrt[n]{a}\)і\(a^{m/n} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m \)

    Якщо\(n\) рівний, то ми вимагаємо\(a ≥ 0\).

    Приклад Template:index

    Запишіть кожен вираз в радикальних позначеннях, потім спростіть.

    1. \((81x^2)^{−1/2}\)
    2. \((243)^{3/5}\)

    Рішення

    1. \((81x^2)^{−1/2} = \dfrac{1}{\sqrt{81x^2}} = \dfrac{1}{9x}\)
    2. \((243)^{3/5} = \sqrt[5]{243^3} = \sqrt[5]{(3^5)^3} = \sqrt[5]{(3^3)^5} = 3^3 = 27\)

    Спрощення радикалів

    Використовуйте якомога частіше властивість\(\sqrt[n]{a^n} = a\) спрощувати радикали. Фактор на шматки, де повноваження дорівнюють індексу\(n\), а потім встановіть ці числа або змінну вільну від радикала! Знову ж таки, ви можете припустити, що у всіх задачах змінні представляють позитивні дійсні числа.

    Приклад Template:index
    1. \(\sqrt{12x^5y^3}\)
    2. \(5\sqrt[3]{216u^6v^5}\)
    3. \(−\sqrt[4]{16a^{23}}\)

    Рішення

    1. \(\begin{array} &\sqrt{12x^5y^3} &= \sqrt{12} \cdot \sqrt{x^5} \cdot \sqrt{y^3} &\text{The product property: simplify \(3\)окремі радикали.}\\ &=\ sqrt {\ textcolor {червоний} {2^2}\ cdot 3}\ cdot\ sqrt {\ textcolor {x^2}\ dot\ textcolor {червоний} {x^2}\ точка x}\ cdot\ sqrt {\ колір тексту {червоний} {y^2}\ cdot y}\ text {індекс\(n = 2\). Знайдіть повноваження\(2\) для спрощення.}\\ &=\ sqrt {2^2\ cdot x^2\ cdot x^2\ cdot y^2}\ cdot\ sqrt {3xy} &\ text {Групуйте квадрати. Групуйте неквадрати.}\\ &= 2\ cdot x\ cdot x\ cdot y\ cdot\ cdot\ sqrt {3xy} n &\ text {Спрощення використання\(\sqrt[n]{a^n} = a\).}\\ &= 2x^2y\ sqrt {3xy} &\ text {Об'єднати повноваження для спрощення.} \ end {масив}\)
    1. \(\begin{array} &5\sqrt[3]{216u^6v^5} &= 5\sqrt[3]{216} \cdot \sqrt[3]{u^6} \cdot \sqrt[3]{v^5} &\;\;\;\text{The product property: simplify \(3\)роздільні радикали.}\\ &= 5\ cdot\ sqrt [3] {\ textcolor {червоний} {6^3}}\ cdot\ sqrt [3] {\ textcolor {червоний} {\ textcolor {v^3}\ cdot v^2}}\ cdot\;\;\ текст {Індекс\(n = 3\). Знайдіть повноваження\(3\) для спрощення.}\\ &= 5\ cdot\ sqrt [3] {6^3\ cdot (u^2) ^3\ cdot v^3}\ cdot\ sqrt [3] {v^2} &\;\;\ text {Групуйте куби. Згрупуйте не-куби.}\\ &= 5\ cdot 6\ cdot u^2\ cdot v\ cdot\ sqrt [3] {v^2} &\;\;\ text {Спрощення використання\(\sqrt[n]{a^n} = a\).}\\ &= 30u^2v\ sqrt [3] {v^2} &\;\;\;\ text {Об'єднати повноваження для спрощення.} \ end {масив}\)
    1. \(\begin{array} &−\sqrt[4]{16a^{23}} &= -1 \cdot \sqrt[4]{16} \cdot \sqrt[4]{a^{23}} &\;\;\;\;\;\;\;\;\;\;\;\text{The product property: simplify \(2\)окремі радикали.}\\ &= −1\ cdot\ sqrt [4] {\ textcolor {червоний} {2^4}}\ cdot\ sqrt [4] {\ textcolor {(a^5) ^4}\ cdot a^3} &\;\;\;\;\;\;\;\;\ text {Скільки разів робить\(4\) йти в\(23\) рівномірно? \(5\). \(R=3\).}\\ &= −1\ cdot\ sqrt [4] {4^2\ cdot (a^5) ^4}\ cdot\ sqrt [4] {a^3} &\;\;\;\;\;\;\;\;\;\;\;\;\ text {Група повноважень\(4\). Групувати неповноваження\(4\).}\\ &= −1\ cdot 2\ cdot a^5\ cdot\ sqrt [4] {a^3} &\;\;\;\;\;\;\;\;\;\;\;\ text {Спрощення використання\(\sqrt[n]{a^n} = a\).}\\ &= -2a^5\ sqrt [4] {a^3} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ text {Об'єднати повноваження для спрощення.} \ end {масив}\)
    Приклад Template:index

    Примножуємо і спрощуємо\(\sqrt[3]{4p^2q^3} \cdot \sqrt[3]{6pq}\)

    Рішення

    \(\begin{array} &\sqrt[3]{4p^2q^3} \cdot \sqrt[3]{6pq} &= \sqrt[3]{4 \cdot 6 \cdot p^2 \cdot p \cdot q \cdot q} &\text{The product property consolidates the radical.} \\ &= \sqrt[3]{24 \cdot p^3 \cdot q^2} &\text{Consolidate the powers using power properties.} \\ &= \sqrt[3]{\textcolor{red}{2^3} \cdot 3} \cdot \sqrt[3]{\textcolor{red}{p^3}} \cdot \sqrt[3]{q^2} &\text{The product property: simplify \(3\)окремі радикали.}\\ &= −\ sqrt [3] {2^3\ cdot p^3}\ cdot\ sqrt [3] {3q^2} &\ text {Групуйте куби. Згрупуйте не-куби.}\\ &= 2p\ cdot\ sqrt [3] {3q^2} &\ text {Спрощення використання\(\sqrt[n]{a^n} = a\).} \ end {масив}\)

    Спробуйте! (Вправи)

    1. У прикладі\(6.1.2\) b цього розділу зазначено:\(\sqrt[5]{(3^5)^3} = \sqrt[5]{(3^3)^5}\).

    Назвіть властивості, які дозволяють нам прирівняти\((3^5)^3 = (3^3)^5\). Поясніть.

    2. Використовуйте еквівалентність,\(x^{ab} = x^{ba}\) щоб спростити кожне з наступних дій без використання калькулятора.

    1. \(\sqrt[3]{(7^3)^{10}}\)
    2. \(\sqrt[4]{(5^4)^3}\)
    3. \(8\sqrt[5]{(-10^5)^4}\)

    3. Для кожного з перерахованих нижче замініть заявлене число як ступінь індексу. Використовуйте еквівалентність,\(x^{ab} = x^{ba}\) щоб спростити кожне з наведених нижче дій.

    Наприклад:\(\sqrt[3]{8^5} = \sqrt[3]{(2^3)^5} = \sqrt[3]{(2^5)^3} = 2^5 = 32\).

    1. \(\sqrt{16^5}\)
    2. \(−5\sqrt[4]{81^7}\)
    3. \(−9\sqrt[5]{32^6}\)

    Для 4-11 запишіть кожен вираз в радикальних позначеннях, потім спростіть без калькулятора.

    1. \(121^{−1/2}\)
    2. \(32^{2/5}\)
    3. \(125^{−2/3}\)
    4. \((−125)^{2/3}\)
    5. \(\left( \dfrac{81}{100} \right)^{1/2}\)
    6. \(\left( \dfrac{64}{125} \right)^{2/3}\)
    7. \(\left(−\dfrac{64}{125} \right)^{2/3}\)
    8. \(\left( \dfrac{64}{125} \right)^{−2/3}\)

    Для 12-23 спростити вираз. Припустимо, що змінні представляють собою позитивні дійсні числа.

    1. \(\sqrt{18y^3}\)
    2. \(\sqrt[3]{250b^5}\)
    3. \(\sqrt[4]{48x^9}\)
    4. \(\sqrt[5]{−243c^{10}}\)
    5. \(−2a \sqrt[10]{80a}\)
    6. \(\dfrac{\sqrt[3]{500u^5}}{45u}\)
    7. \(\sqrt[4]{\dfrac{1250p^9}{p^{13}}}\)
    8. \(\dfrac{3}{4} \sqrt{\dfrac{96z^{20}}{6}}\)
    9. \(\sqrt{128n^{10}m^3}\)
    10. \(\sqrt[4]{\dfrac{405x^{14}y^6}{5x^4y}}\)
    11. \((\sqrt[7]{a^5b^6})^{35}\)
    12. \(\left( \dfrac{\sqrt[3]{8u^6v^{12}}}{6u^2v} \right)^2\)

    За 24-31 помножити і спростити. Припустимо, що змінні представляють собою позитивні дійсні числа.

    1. \(−3x \sqrt{5x} \cdot \sqrt{20x^3}\)
    2. \(2q \sqrt[3]{54q^2} \cdot \sqrt[3]{4q^4}\)
    3. \(6t^3 (\sqrt[4]{75t^6} \cdot \sqrt[4]{100t^3})\)
    4. \(\sqrt[5]{64u^5v^8 } \cdot \sqrt[5]{112v^4} \cdot 7v\)
    5. \(\dfrac{\sqrt{5x}}{10} \cdot \dfrac{\sqrt{15x}}{3x}\)
    6. \(\dfrac{1}{2} \left( \dfrac{\sqrt[3]{18a^2}}{2} \right) \left( \dfrac{\sqrt[3]{6a^4}}{3a} \right)\)
    7. \(\sqrt[3]{\dfrac{56n^4}{27m^5}} \cdot \sqrt[3]{\dfrac{49m^2}{8n}}\)
    8. \(\left( \dfrac{24w^{11}}{13} \right)^3 \left( \dfrac{13w}{6} \right)^3 \)