1.E: Тригонометричні функції (вправи)

Last updated
Save as PDF

Page ID: 59367

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Вправа$\PageIndex{1}$

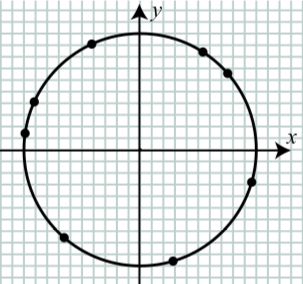
На наступній схемі показано вісім точок, нанесених на одиничному колі. Ці точки відповідають наступним значенням, коли числова лінія обертається навколо одиничного кола.

$t = 1, t = 2, t = 3, t = 4, t = 5, t = 6, t = 7$, і$t = 9$.

$1.1.1.png$

Малюнок$\PageIndex{1}$

(a) Позначте кожну точку на діаграмі її значенням$t$.

(б) Орієнтовні координати точок, що відповідають$t = 1, t = 5$, і$t=9$.

Відповідь

$t$	точка
\ (t\) ">$1$	$(0.54, 0.84)$
\ (t\) ">$5$	$(0.28, -0.96)$
\ (t\) ">$9$	$(-0.91, 0.41)$

Вправа$\PageIndex{2}$

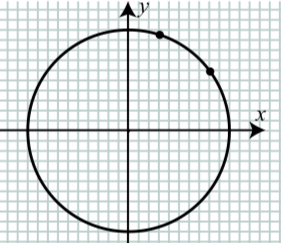
На наступній схемі показані точки, що відповідають$t = \dfrac{\pi}{5}$ і$t = \dfrac{2\pi}{5}$ коли числова лінія обертається навколо одиничного кола.

$1.1.2.png$

Малюнок$\PageIndex{2}$

На цьому одиничному колі намалюйте точки$t = \dfrac{4\pi}{5}$, відповідні$t = \dfrac{5\pi}{6}$,$t = \dfrac{8\pi}{5}$ і$t = \dfrac{10\pi}{5}$.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Вправа$\PageIndex{3}$

Намалюйте наступні дуги на одиничному колі.

(а) Дуга, яка визначається інтервалом$[0, \dfrac{\pi}{6}]$ на числовій лінії.

(б) Дуга, яка визначається інтервалом$[0, \dfrac{7\pi}{6}]$ на числовій лінії.

(г) Дуга, яка визначається інтервалом$[0, -\dfrac{4\pi}{5}]$ на числовій лінії.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Вправа$\PageIndex{4}$

Визначте квадрант, який містить кінцеву точку кожної заданої дуги з початковою точкою$(1, 0)$ на одиничному колі.

(а)$\dfrac{7\pi}{4}$

(б)$\dfrac{-7\pi}{4}$

(c)$\dfrac{5\pi}{3}$

(г)$\dfrac{-5\pi}{3}$

(е)$\dfrac{7\pi}{3}$

(f)$\dfrac{-7\pi}{3}$

(г)$\dfrac{5\pi}{8}$

(ч)$\dfrac{-5\pi}{8}$

(i)$2.5$

(j)$-2.5$

(К)$3$ (л)$3+2\pi$

(м)$3-\pi$

(п)$3-2\pi$

Відповідь

	$(a)$	$(b)$	$(d)$	$(i)$	$(j)$	$(l)$	$(m)$
$t$	\ (a)\)» клас = "lt-математика-17332">$\dfrac{7\pi}{4}$	\ (b)\)» клас = "lt-математика-17332">$-\dfrac{7\pi}{4}$	\ (d)\)» клас = "lt-математика-17332">$-\dfrac{3\pi}{5}$	\ (i)\)» клас = "lt-математика-17332">$2.5$	\ (j)\)» клас = "lt-математика-17332">$-2.5$	\ ((l)\)» клас = «lt-математика-17332">$3 + 2\pi$	\ (m)\)» клас = "lt-математика-17332">$3 - \pi$
Квадрант	\ (a)\)» Клас ="ЛТ-математика-17332">IV	\ (b)\)» Клас = "ЛТ-математика-17332">I	\ (d)\)» Клас = "ЛТ-математика-17332">III	\ (i)\)» Клас = "ЛТ-математика-17332">II	\ (j)\)» Клас ="ЛТ-математика-17332">III	\ (l)\)» Клас = "ЛТ-математика-17332">II	\ (m)\)» Клас ="ЛТ-математика-17332">IV

Вправа$\PageIndex{5}$

Знайдіть всі точки на одиничному колі:

(a) Чия x-координата$\dfrac{1}{3}$

(b) Чия y-координата$-\dfrac{1}{2}$

(d) Чия$-\dfrac{3}{4}$ y-координата та чия$x$ -координата від'ємна.

Додайте сюди текст. Щоб автоматичний номер працював, потрібно додати шаблон «AutoNum» (бажано в кінці) на сторінку.

Відповідь

(а) Підставляємо$x = \dfrac{1}{3}$ в рівняння$x^{2} + y^{2} = 1$. Вирішуючи для$y$, отримуємо$y = \pm\dfrac{\sqrt{8}}{3}$. Так що точки є$(\dfrac{1}{3}, \dfrac{\sqrt{8}}{3})$ і$(\dfrac{1}{3}, -\dfrac{\sqrt{8}}{3})$.

(б) Підставляємо$y = -\dfrac{1}{2}$ в рівняння$x^{2} + y^{2} = 1$. Вирішуючи для$x$, отримуємо$x = \pm\dfrac{\sqrt{3}}{3}$. Так що точки є$(\dfrac{\sqrt{8}}{3}, -\dfrac{1}{3})$ і$(-\dfrac{\sqrt{3}}{3}, -\dfrac{1}{2})$.

Вправа$\PageIndex{6}$

Заповніть пробіли для кожного з наступних дій:

Для дійсного числа$t$ значення$\cos(t)$ визначається як () - координата () точки дуги t, початкова точка якої () на () рівняння якої є$x^2 + y^2 = 1$.
Домен функції косинуса - ().
Максимальне значення$\cos(t)$ is () і це відбувається при$t$ = () for$0 \leq t < 2\pi$. Мінімальне значення$\cos(t)$ is () і це відбувається при$t$ = () for$0 \leq t < 2\pi$.
Діапазон функції косинуса дорівнює ().

Відповідь

1. Для дійсного числа$t$ значення$\cos(t)$ визначається як x -координата кінцевої точки дуги, початкова точка$t$ якої знаходиться $(1, 0)$на одиничному колі, рівняння якої є$x^{2} + y^{2} = 1$.

2. Домен функції косинуса - це множина всіх дійсних чисел.

3. Максимальне значення$\cos(t)$ дорівнює 1 і це відбувається при$t =$ 0 for$1 \leq t < 2\pi$. Мінімальне значення$\cos(t)$ дорівнює -1 і це відбувається при$t = \pi$ for$0 \leq t < 2\pi$.

4. Діапазон функції косинуса - замкнутий інтервал$[-1,1]$.

Вправа$\PageIndex{7}$

Заповніть пробіли для кожного з наступних дій:

Для дійсного числа$t$ значення sin$(t)$ визначається як () - координата () точки дуги t, початкова точка якої () на () рівняння якої є$x^2 + y^2 = 1$.
Домен синусоїдної функції - ().
Максимальне значення$\sin(t)$ is () і це відбувається при$t$ = () for$0 \leq t < 2\pi$. Мінімальне значення$\sin(t)$ is () і це відбувається при$t$ = () for$0 \leq t < 2\pi$.
Діапазон синусоїдальної функції дорівнює ().

Відповідь

(а)$\cos(t) = \dfrac{4}{5}$ або$\cos(-\dfrac{4}{5})$.

(c)$\sin(t) = -\dfrac{-\sqrt{5}}{3}$.

Вправа$\PageIndex{8}$

Заповніть наступну таблицю значень:

Довжина дуги на одиничному колі	Кінцева точка дуги	$\cos(t)$	$\sin(t)$
$0$	$(1, 0)$	$1$	$0$
$\dfrac{\pi}{2}$
$\pi$
$\dfrac{3\pi}{2}$
$2\pi$

Заповніть наступну таблицю значень:

Довжина дуги на одиничному колі	Кінцева точка дуги	$\cos(t)$	$\sin(t)$
$0$	$(1, 0)$	$1$	$0$
$-\dfrac{\pi}{2}$
$-\pi$
$-\dfrac{3\pi}{2}$
$-2\pi$

Заповніть наступну таблицю значень:

Довжина дуги на одиничному колі	Кінцева точка дуги	$\cos(t)$	$\sin(t)$
$2\pi$	$(1, 0)$	$1$	$0$
$\dfrac{5\pi}{2}$
$3\pi$
$\dfrac{7\pi}{2}$
$4\pi$

Вправа$\PageIndex{9}$

Які можливі значення,$\cos(t)$ якщо відомо, що$\sin(t) = \dfrac{3}{5}$?
Які можливі значення,$\cos(t)$ якщо відомо, що$\sin(t) = \dfrac{3}{5}$ і кінцева точка$t$ знаходиться у другому квадранті?
Що таке значення,$\sin(t)$ якщо відомо, що$\cos(t) = \dfrac{-2}{3}$ і кінцева точка$t$ знаходиться в третьому квадранті?

Вправа$\PageIndex{10}$

Припустимо, відомо, що$0 < \cos(t) < \dfrac{1}{3}$.

Склавши в квадрат вирази в заданих нерівностях, про які висновки можна зробити$\cos^2(t)$?
Використовуйте частину (а) для написання нерівностей, що включають,$-\cos^2(t)$ а потім нерівності за участю$1 - \cos^2(t)$.
Використовуючи піфагорійську ідентичність, ми бачимо це$\sin^2(t) = 1 - \cos^2(t)$. Запишіть останню нерівність в частині (b) в терміні$\sin^2(t)$.
Якщо ми також знаємо$\sin(t) > 0$, що, що ми можемо зробити висновок про вартість$\sin(t)$?

Відповідь

(а)$0 < \cos^{2}(t) < \dfrac{1}{9}$.

(б)$-\dfrac{1}{9} < -\cos^{2}(t) < 0$ і так$\dfrac{8}{9} < 1 - \cos^{2}(t) < 1$

(c)$\dfrac{8}{9} < \sin^{2}(t) < 1$

(г)$\dfrac{\sqrt{8}}{3} < \sin(t) < 1$

Вправа$\PageIndex{11}$

Використовуйте процес, подібний до процесу у вправі (5), щоб виконати кожну з наступних дій:

Припустимо, відомо, що$-\dfrac{1}{4} < sin(t) < 0$ і що$\cos(t) > 0$. Про що можна зробити висновок$\cos(t)$?
Припустимо, відомо, що$ 0 \leq \sin(t) \leq \dfrac{3}{7}$ і що$\cos(t) < 0$. Про що можна зробити висновок$\cos(t)$?

Вправа$\PageIndex{12}$

Використовуючи чотиризначні наближення для значень косинуса та синуса у Вправі 1.6, обчислити кожне з наступних параметрів:

$\cos^2(1) + \sin^2(1)$
$\cos^2(2) + \sin^2(2)$
$\cos^2(-4) + \sin^2(-4)$
$\cos^2(15) + \sin^2(15)$

Яким має бути точне значення кожного з цих обчислень? Чому результати не дорівнюють цьому точному значенню?

Вправа$\PageIndex{13}$

Перетворіть кожне з наступних вимірювань ступеня для кутів у радіанові заходи для кутів. У кожному випадку спочатку запишіть результат у вигляді дробового кратного,$\pi$ а потім скористайтеся калькулятором, щоб отримати наближення радіановної міри з 4 знаками після коми.

(а)$15^\circ$ (б)$58^\circ$ (c)$112^\circ$ (d)$210^\circ$ (е)$-40^\circ$ (f)$-78^\circ$

Вправа$\PageIndex{14}$

Перетворіть кожне з наступних радіанових вимірювань для кутів у градусні заходи для кутів. При необхідності запишіть кожен результат як наближення до 4 знаків після коми.

(a)$\dfrac{3}{8}\pi$ радіани (b)$\dfrac{7}{9}\pi$ радіани (c)$-\dfrac{7}{15}\pi$ радіани (d)$1$ радіани (e)$2.4$ радіани (f)$3$ радіани

Відповідь

(а)$67.5^\circ$

(б)$231. 4268^\circ$

(г)$57.2958^\circ$

Вправа$\PageIndex{15}$

Намалюйте кут у стандартному положенні кута, радіановна міра якого дорівнює:

(а)$\dfrac{1}{4}\pi$ (б)$\dfrac{1}{3}\pi$ (c)$\dfrac{2}{3}\pi$ (d)$\dfrac{5}{4}\pi$ (е)$-\dfrac{1}{3}\pi$ (f)$3.4$

Вправа$\PageIndex{16}$

У вправі 1.16 ми використовували аплет Geogebra під назвою Термінальні точки дуг на Одиничному колі для наближення значень функцій косинуса та синуса. Тепер ми зробимо щось подібне, щоб наблизити значення косинуса і синуса для кутів, виміряних в градусах.

Ми бачили, що кінцева сторона кута в стандартному положенні перетинає одиничну окружність в точці. Ми використовуємо координати цієї точки, щоб визначити косинус і синус цього кута. Коли кут вимірюється в радіанах, радіанська міра кута така ж, як і дуга на одиничній окружності, піднесеної кутом. Це невірно, коли кут вимірюється в градусах, але ми все ще можемо використовувати точку перетину для визначення косинуса та синуса кута. Так що якщо кут в стандартному положенні має ступінь вимірювання$a^\circ$, то ми визначаємо,$\cos(a^\circ)$ щоб бути координата х точки перетину кінцевої сторони цього кута і одиниці окружності. Ми$\sin(a^\circ)$ визначаємо y-координату точки перетину кінцевої сторони цього кута та одиничної окружності.

Тепер ми будемо використовувати аплет Geogebra Кути і одиничне коло. Веб-адреса для цього аплету:

http://gvsu.edu/s/VG

Для цього аплету ми керуємо значенням вхідних даних$a^\circ$ повзунком for$a$. Значення діапазону від$-180^\circ$ до$180^\circ$ з кроком$5^\circ$. Для заданого значення$a^\circ$ викреслюється кут в стандартному положенні і відображаються координати точки перетину кінцевої сторони цього кута і одиничного кола. Використовуйте цей аплет для наближення значень для кожного з наведених нижче параметрів:

(а)$\cos(10^\circ)$ і$\sin(10^\circ)$

(б)$\cos(60^\circ)$ і$\sin(60^\circ)$

(c)$\cos(135^\circ)$ і$\sin(135^\circ)$

(г)$\cos(-10^\circ)$ і$\sin(-10^\circ)$

(е)$\cos(-135^\circ)$ і$\sin(-135^\circ)$

(f)$\cos(85^\circ)$ і$\sin(85^\circ)$

Відповідь

(а)$\cos(10^\cric) \approx 0.9848, \sin(10^circ) \approx 0.1736$

(б)$\cos(-10^\cric) \approx 0.9848, \sin(-10^circ) \approx -0.1736$

Вправа$\PageIndex{17}$

Вправа (4) повинна бути виконана перед виконанням цієї вправи. Помістіть калькулятор, який ви використовуєте, у режимі «Ступінь». Потім скористайтеся калькулятором для визначення значень функцій косинуса та синуса у Вправі (4). Чи однакові значення? Чим вони відрізняються?

Вправа$\PageIndex{18}$

Визначте довжину дуги (до найближчої сотої одиниці, коли це необхідно) для кожного з наступних.

(а) Дуга на колі радіусом 6 футів, яка перехоплюється центральним кутом$\dfrac{2\pi}{3}$ радіанів. Порівняйте це з однією третиною окружності кола.

(b) Дуга на колі радіусом 100 миль, яка перехоплюється центральним кутом 2 радіани.

(d) Дуга на колі радіусом 10 футів, яка перехоплюється центральним кутом 152 градуси.

Відповідь

(а) Довжина дуги -$4\pi$ фути, яка дорівнює$\dfrac{1}{3}$ окружності кола.

(б) Довжина дуги -$200$ милі.

(в) Довжина дуги -$26\pi$ метри.

Вправа$\PageIndex{19}$

У кожному з наступних, коли це можливо, визначають точну міру центрального кута в радіанах. В іншому випадку округляйте до найближчої сотої частки радіана.

(а) Центральний кут, який перехоплює дугу довжиною$3$ футів на колі радіусних$5$ футів.

(b) Центральний кут, який перехоплює дугу довжиною$18$ футів на колі радіусних$5$ футів.

Відповідь

(а)$\theta = \dfrac{3\pi}{5}$ радіани.

(б)$\theta = \dfrac{18}{5}$ радіани$= 3.6$ радіани.

Вправа$\PageIndex{20}$

У кожному з наступних, коли це можливо, визначають точну міру центрального кута в градусах. В іншому випадку округляйте до найближчої сотої градуса.

(а) Центральний кут, який перехоплює дугу довжиною 3 фути на колі радіусом 5 футів.

(б) Центральний кут, який перехоплює дугу довжиною 18 футів на колі радіусом 5 футів.

(d) Центральний кут, який перехоплює дугу довжиною 5 дюймів на колі радіусом 5 дюймів.

(е) Центральний кут, який перехоплює дугу довжиною 12 дюймів на колі радіусом 5 дюймів.

Відповідь

(а)$\theta = 108^\circ$

(б)$\theta = (\dfrac{648}{\pi})^\circ \approx 206.26^\circ$

Вправа$\PageIndex{21}$

Визначте відстань (в милі), яке планета Марс подорожує за один тиждень на своєму шляху навколо Сонця. Для цієї проблеми припустимо, що Марс завершує один повний оборот навколо Сонця за 687 днів і що шлях Марса навколо Сонця являє собою коло радіусом 227,5 мільйонів миль.

Вправа$\PageIndex{22}$

Визначте відстань (в милі), яке Земля подорожує за один день на своєму шляху навколо Сонця. Для цієї проблеми припустимо, що Земля завершує один повний оборот навколо Сонця за 365,25 днів і що шлях Землі навколо Сонця являє собою коло радіусом 92,96 мільйона миль.

Вправа$\PageIndex{23}$

Компактний диск (CD) має діаметр 12 сантиметрів (см). Припустимо, що компакт-диск знаходиться в CD-плеєрі і обертається зі швидкістю 225 оборотів в хвилину. Що таке кутова швидкість CD (в радіанах в секунду) і яка лінійна швидкість точки на краю КД?

Вправа$\PageIndex{24}$

Людина їде на колесі огляду, якому потрібно 28 секунд, щоб зробити повний оборот. Її сидіння знаходиться на відстані 25 футів від осі колеса.

(а) Яка її кутова швидкість в оборотах в хвилину? Радіани в хвилину? Градусів в хвилину?

(б) Яка її лінійна швидкість?

(c) Яка з величин кутова швидкість і лінійна швидкість змінюються, якщо сидіння людини було 20 футів від осі замість 25 футів? Обчислити нове значення для будь-якого значення, яке змінюється. Поясніть, чому кожне значення змінюється або не змінюється.

Вправа$\PageIndex{25}$

Невеликий шків радіусом$3$ дюймів з'єднується ременем з більшим шківом радіусом$7.5$ дюймів (див. Малюнок$\PageIndex{3}$). Менший шків підключений до двигуна, що змушує його обертатися проти годинникової стрілки зі швидкістю оборотів в$120$ хвилину (оборотів в хвилину). Оскільки два шківи з'єднані ременем, більший шків також обертається проти годинникової стрілки.

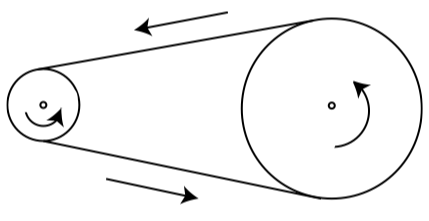
$1.16.пнг$

Малюнок$\PageIndex{3}$: Два шківи, з'єднані ременем

(а) Визначити кутову швидкість меншого шківа в радіанах в хвилину.

(b) Визначити лінійну швидкість обода меншого шківа в дюймах в хвилину.

(d) Знайти кутову швидкість більшого шківа в радіанах в секунду.

(e) Скільки обертів в хвилину більший шків повороту?

Відповідь: (б)$v = 720\pi\dfrac{in}{min} \approx 2261.95\dfrac{in}{min}$

Вправа$\PageIndex{26}$

Невеликий шків радіусом$10$ сантиметрів дюймів з'єднується ременем з більшим шківом радіусом$24$ сантиметрів дюймів (див. Рис. Більший шків підключений до двигуна, що змушує його обертатися проти годинникової стрілки зі швидкістю оборотів в$75$ хвилину (оборотів в хвилину). Оскільки два шківи з'єднані ременем, менший шків також обертається проти годинникової стрілки.

(а) Визначити кутову швидкість більшого шківа в радіанах в хвилину.

(б) Визначити лінійну швидкість обода великого шківа в дюймах в хвилину.

(d) Знайти кутову швидкість меншого шківа в радіанах в секунду.

(e) Скільки обертів в хвилину менший шків повороту?

Відповідь: (б)$v = 3600\pi\dfrac{cm}{min} \approx 11309.73\dfrac{cm}{min}$

Вправа$\PageIndex{27}$

Радіус колеса автомобіля становить 15 дюймів. Якщо автомобіль їде 60 миль на годину, яка кутова швидкість колеса в радіанах в хвилину? Як швидко обертається колесо в оборотах в хвилину?

Вправа$\PageIndex{28}$

Середня відстань від Землі до Місяця становить 238,857 миль. Припускаючи, що орбіта Місяця навколо Землі являє собою коло радіусом 238 857 миль і що Місяць робить один оборот навколо Землі кожні 27,3 дня, визначають лінійну швидкість Місяця в милі на годину. Дослідіть відстань Місяця до Землі та поясніть, чому щойно зроблені обчислення є наближеннями

Вправа$\PageIndex{29}$

Одиничне коло показано в кожному з наступних, що показує інформацію про дугу$t$. У кожному конкретному випадку використовуйте інформацію по одиничному колу для визначення значень$t$$\cos(t)$, і$\sin(t)$.

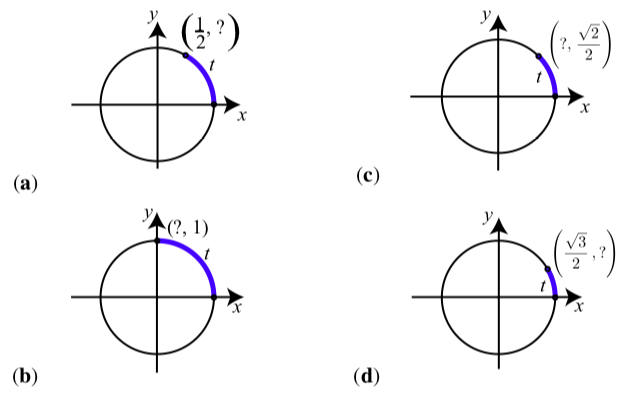
$e1.png$

Малюнок$\PageIndex{4}$

Відповідь

(а)$t = \dfrac{\pi}{3}, \cos(t) = \dfrac{1}{2}, \sin(t) = \dfrac{\sqrt{3}}{2}$.

(б)$t = \dfrac{\pi}{2}, \cos(t) = 0, \sin(t) = 1$.

(c)$t = \dfrac{\pi}{4}, \cos(t) = \dfrac{\sqrt{2}}{2}, \sin(t) = \dfrac{\sqrt{2}}{2}$.

(г)$t = \dfrac{\pi}{6}, \cos(t) = \dfrac{\sqrt{3}}{2}, \sin(t) = \dfrac{1}{2}$.

Вправа$\PageIndex{30}$

Визначте точне значення для кожного з наступних виразів, а потім скористайтеся калькулятором для перевірки результату. Наприклад,

\[\cos(0) + \sin(\dfrac{\pi}{3}) = 1 + \dfrac{\sqrt{3}}{2} \approx 1.8660.\]

(а)\[\cos^2(\dfrac{\pi}{6})\]

(б)\[2\sin^2(\dfrac{\pi}{6}) + \cos(\pi)\]

(c)\[\dfrac{\cos(\dfrac{\pi}{6})}{\sin(\dfrac{\pi}{6})}\]

(г)\[3\sin(\dfrac{\pi}{2}) + \cos(\dfrac{\pi}{4})\]

Відповідь

(а)$\cos^{2}(\dfrac{\pi}{6}) = \dfrac{3}{2}$.

(б)$2\sin^{2}(\dfrac{\pi}{4}) + \cos(\pi) = 0$.

Вправа$\PageIndex{31}$

Для кожного з наступних визначте опорну дугу для даної дуги і намалюйте дугу і її опорну дугу на одиничному окружності.

(а)$t = \dfrac{4\pi}{3}$

(б)$t = \dfrac{13\pi}{8}$

(c)$t = \dfrac{9\pi}{4}$

(г)$t = -\dfrac{4\pi}{3}$

(е)$t = -\dfrac{7\pi}{5}$ (f)$t = 5$

Відповідь

(а) Опорна дуга є$\dfrac{\pi}{3}$.

(б) Опорна дуга є$\dfrac{3\pi}{8}$.

(г) Опорна дуга є$\dfrac{\pi}{3}$.

Вправа$\PageIndex{32}$

Для кожного з наступних намалюйте задану дугу t на одиничній окружності, визначте опорну дугу для t, а потім визначте точні значення для$cos(t)$ і$sin(t)$.

(а)$t = \dfrac{5\pi}{6}$

(б)$t = \dfrac{5\pi}{4}$

(c)$t = \dfrac{5\pi}{3}$

(г)$t = -\dfrac{2\pi}{3}$

(е)$t = -\dfrac{7\pi}{4}$

(f)$t = \dfrac{19\pi}{6}$

Відповідь

(а) опорна дуга є$\dfrac{\pi}{6}$$\cos(\dfrac{5\pi}{6}) = -\dfrac{\sqrt{3}}{2}$;$\sin(\dfrac{5\pi}{6}) = -\dfrac{1}{2}$.

(б) опорна дуга є$\dfrac{\pi}{3}$$\cos(-\dfrac{2\pi}{3}) = -\dfrac{1}{2}$;$\sin(-\dfrac{2\pi}{3}) = -\dfrac{\sqrt{3}}{2}$.

Вправа$\PageIndex{33}$

(а) Використовуйте калькулятор (в радіановому режимі) для визначення п'ятизначних наближень для$\cos(4)$ і$\sin(4)$.

(b) Використовуйте калькулятор (в радіановому режимі) для визначення п'ятизначних наближень для$\cos(4 - \pi)$ і$\sin(4 - \pi)$.

Вправа$\PageIndex{34}$

Припустимо, що у нас є наступна інформація про дузі$t$.

\[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{1}{5}\]

Використовуйте цю інформацію для визначення точних значень кожного з наступних:

(а)$\cos(t)$

(б)$\sin(\pi - t)$

(c)$\cos(\pi - t)$

(г)$\sin(\pi + t)$

(е)$\cos(\pi + t)$

(f)$\sin(2\pi - t)$

Відповідь

(а)$\cos(t) = \dfrac{\sqrt{24}}{5}$.

(г)$\sin(\pi + t) = -\dfrac{1}{5}$.

Вправа$\PageIndex{35}$

Припустимо, що у нас є наступна інформація про дузі$t$.

\[\dfrac{\pi}{2} < t < \pi \space and \space \cos(t) = -\dfrac{2}{3}\]

Використовуйте цю інформацію для визначення точних значень кожного з наступних:

(а)$\sin(t)$ (б)$\sin(\pi - t)$ (c)$\cos(\pi - t)$ (d)$\sin(\pi + t)$ (е)$\cos(\pi + t)$ (f)$\sin(2\pi - t)$

Вправа$\PageIndex{36}$

Переконайтеся, що ваш калькулятор знаходиться в режимі Radian.

(a) Використовуйте калькулятор, щоб знайти восьмизначне наближення$\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{5\pi}{12})$

(б) Визначити точне значення$\sin(\dfrac{\pi}{6}) + \sin(\dfrac{\pi}{4})$.

(c) Використовуйте калькулятор, щоб знайти восьмизначне наближення вашого результату в частині (b). Порівняйте це з вашим результатом в частині (а). Чи здається, що

\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6}) + sin(\dfrac{\pi}{4}).\]

(г) Визначити точне значення$\sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4})$.

(e) Визначте восьмизначне наближення вашого результату в частині (d).

(f) Порівняйте результати по частинам (а) і (е). Чи здається, що

\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4}).\]

Вправа$\PageIndex{37}$

$e9.png$

Малюнок$\PageIndex{5}$

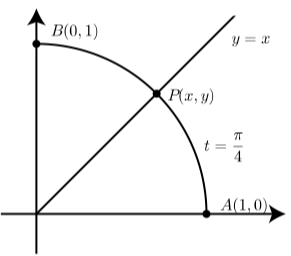
Дана вправа надає альтернативний метод визначення точних значень$\cos(\dfrac{\pi}{4})$ і$\sin(\dfrac{\pi}{4})$. На схемі показана кінцева точка$P(x, y)$ для дуги довжини$t = \dfrac{\pi}{4}$ на одиничному колі. Точки$A(1, 0)$ і$B(0, 1)$ також показані.

Так як точка В - кінцева точка дуги довжини$\dfrac{\pi}{2}$, то можна зробити висновок, що довжина дуги від Р до В теж є$\dfrac{\pi}{4}$. Через це робимо висновок, що точка Р лежить на лінії y D x так, як показано на схемі. Використовуйте цей факт для визначення значень x і y. поясніть, чому це доводить, що\[\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space \sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]

Вправа$\PageIndex{38}$

$e10.png$

Малюнок$\PageIndex{6}$

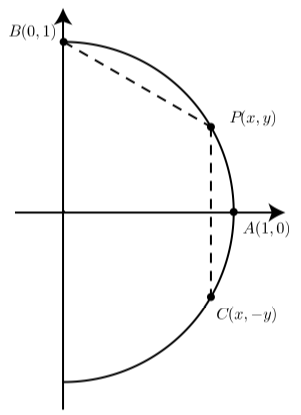
Дана вправа надає альтернативний метод визначення точних значень$\cos(\dfrac{\pi}{6})$ і$\sin(\dfrac{\pi}{6})$. На схемі показана кінцева точка$P(x, y)$ для дуги довжини$t = \dfrac{\pi}{6}$ на одиничному колі. Точки$A(1, 0)$$B(0, 1)$, а$C(x, -y)$ також показані. Зверніть увагу, що B є кінцевою точкою на$arc \space t = -\dfrac{\pi}{6}.$
Ми тепер помічаємо, що довжина дуги від P до B є\[\dfrac{\pi}{2} - \dfrac{\pi}{6} = \dfrac{\pi}{3}.\] Крім того, довжина дуги від C до P\[\dfrac{\pi}{6} - \dfrac{-\pi}{6} = \dfrac{\pi}{3}.\]
Це означає, що відстань від P до B дорівнює відстані від C до P.

(a) Використовуйте формулу відстані, щоб написати формулу (через x та y) для відстані від P до B.

(b) Використовуйте формулу відстані, щоб написати формулу (через x і y) для відстані від C до P.

(c) Встановіть відстані від (a) і (b) рівні один одному і вирішіть отримане рівняння для y Для цього почніть з квадратизації обох сторін рівняння. Для того щоб вирішити для y, може знадобитися використовувати той факт, що$x^2 + y^2 = 1$.

(г) Використовуйте значення для y в (c) і той факт, що x2 C y2 D 1 для визначення значення для х Поясніть, чому це доводить, що\[\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{1}{2}.\]

Вправа$\PageIndex{39}$

$e11.png$

Малюнок$\PageIndex{7}$

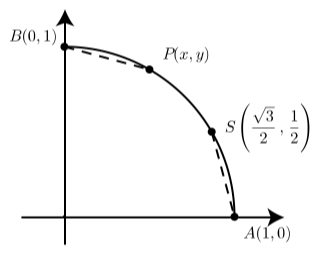
Дана вправа надає альтернативний метод визначення точних значень$\cos(\dfrac{\pi}{3})$ і$\sin(\dfrac{\pi}{3})$. На схемі показана кінцева точка$P(x, y)$ для дуги довжини$t = \dfrac{\pi}{3}$ на одиничному колі. Точки$A(1, 0)$$B(0, 1)$, а$S(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})$ також показані. Зверніть увагу, що B є кінцевою точкою$arc \space t = \dfrac{\pi}{2}.$ Повідомлення, що B є кінцевою точкою$arc \space t = \dfrac{\pi}{2}.$

З вправи (10) ми знаємо, що$S$ це кінцева точка дуги довжини$\dfrac{\pi}{6}$.

Тепер помічаємо, що довжина дуги від$A$ до$P$ є$\dfrac{\pi}{3}$. Крім того, так як довжина дуги від$A$ до$B$ є$\dfrac{\pi}{2}$ і і довжина дуги від$B$ до$P$ є$\dfrac{\pi}{3}$. Це означає, що відстань від$P$ до$B$ дорівнює\[\dfrac{\pi}{2} - \dfrac{\pi}{3} = \dfrac{\pi}{6}.\] Оскільки обидві дуги мають довжину$\dfrac{\pi}{6}$, відстань від$A$ до$S$ дорівнює відстані від$P$ до$B$.

(а) Використовуйте формулу відстані, щоб написати формулу (через x та y) для відстані від$P$ до$B$.

(b) Використовуйте формулу відстані, щоб написати формулу (через x та y) для відстані від$P$ до$B$.

(c) Встановити відстані від (a) і (b) рівні один одному і вирішити отримане рівняння для$y$. Для цього почніть з зведення в квадрат обидві сторони рівняння. Для того щоб вирішити для y, може знадобитися використовувати той факт, що$x^2 + y^2 = 1$.

(d) Використовувати значення для$y$ in (c) і той факт, що$x^2 + y^2 = 1$ для визначення значення для$x$.

Поясніть, чому це доводить, що\[\cos(\dfrac{\pi}{3}) = \dfrac{1}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}.\]

Вправа$\PageIndex{40}$

Заповніть наступну таблицю точними значеннями кожного функціонального значення, якщо воно визначено.

$t$	$\cot(t)$	$\sec(t)$	$\csc(t)$
$0$
$\dfrac{\pi}{6}$
$\dfrac{\pi}{4}$
$\dfrac{\pi}{4}$
$\dfrac{\pi}{2}$

Відповідь

$t$	$\cos(t)$	$\sec(t)$	$\csc(t)$
$0$	невизначений	$1$	невизначений
$\dfrac{\pi}{6}$	$\sqrt{3}$	$\dfrac{2}{\sqrt{3}}$	$2$
$\dfrac{\pi}{4}$	$1$	$\sqrt{2}$	$\sqrt{2}$
$\dfrac{\pi}{3}$	$\dfrac{1}{\sqrt{3}}$	$2$	$\dfrac{2}{\sqrt{3}}$
$\dfrac{\pi}{2}$	$0$	невизначений	$1$

Вправа$\PageIndex{41}$

Заповніть наступну таблицю точними значеннями кожного функціонального значення, якщо воно визначено.

$t$	$\cot(t)$	$\sec(t)$	$\csc(t)$
$\dfrac{2\pi}{3}$
$\dfrac{7\pi}{6}$
$\dfrac{7\pi}{4}$
$-\dfrac{\pi}{3}$
$\pi$

Вправа$\PageIndex{42}$

Визначте квадрант, в якому лежить кінцева точка кожної дуги, виходячи з заданої інформації.

$\cos(x) > 0$і$\tan(x) < 0$
$\tan(x) > 0$і$\csc(x) < 0$
$\cot(x) > 0$і$\sec(x) > 0$
$\sin(x) < 0$і$\sec(x) > 0$
$\sec(x) < 0$і$\csc(x) > 0$
$\sin(x) < 0$і$\cot(x) > 0$

Відповідь

(а) Кінцева точка знаходиться в четвертому квадранті.

(б) Кінцева точка знаходиться в третьому квадранті.

Вправа$\PageIndex{43}$

Якщо$\sin(t) = \dfrac{1}{3}$ і$\cos(t) < 0$, визначте точні значення$\cos(t)$,$\tan(t)$,$\csc(t)$,$\sec(t)$, і$\cot(t)$.

Відповідь

$\cos(t) = -\dfrac{\sqrt{8}}{3}$
$\tan(t) = -\dfrac{1}{\sqrt{8}}$
$\csc(t) = 3$
$\sec(t) = -\dfrac{3}{\sqrt{8}}$
$\cot(t) = -\sqrt{8}$

Вправа$\PageIndex{44}$

Якщо$\cos(t) = -\dfrac{3}{5}$ і$\sin(t) < 0$, визначте точні значення$\sin(t)$,$\tan(t)$,$\csc(t)$,$\sec(t)$, і$\cot(t)$.

Вправа$\PageIndex{45}$

Якщо$\sin(t) = -\dfrac{2}{5}$ і$\tan(t) < 0$, визначте точні значення$\cos(t)$,$\tan(t)$,$\csc(t)$,$\sec(t)$, і$\cot(t)$.

Вправа$\PageIndex{46}$

Якщо$\sin(t) = 0. 273$ і$\cos(t) < 0$, визначте п'ятизначні наближення для$\cos(t)$,$\tan(t)$,$\csc(t)$,$\sec(t)$, і$\cot(t)$.

Вправа$\PageIndex{47}$

У кожному конкретному випадку визначте дугу t, яка задовольняє заданих умов або поясніть, чому такої дуги не існує.

$\tan(t) = 1, \cos(t) = -\dfrac{1}{\sqrt{2}}, and 0< t < 2\pi$
$\sin(t) = 1, \sec(t)$не визначено, і$0< t < \pi$
$\sin(t) = \dfrac{\sqrt{2}}{2}, \sec(t) = -\sqrt{2}, and 0< t < \pi$
$\sec(t) = -\dfrac{2}{\sqrt{3}}, \tan(t) = \sqrt{2}, and 0< t < 2\pi$
$\csc(t) = \sqrt{2}, \tan(t) = -1, and 0< t < 2\pi$

Відповідь

(а)$t = \dfrac{5\pi}{4}$

(б)$t = \dfrac{\pi}{2}$

Вправа$\PageIndex{48}$

Використовуйте калькулятор для визначення чотиризначних десяткових наближень для кожного з наступних параметрів.

$\csc(1)$
$\tan(\dfrac{12\pi}{5})$
$\cot(t)$
$\sec(\dfrac{13\pi}{8})$
$\sin^2(5.5)$
$1 + \tan^2(2)$
$\sec^2(2)$

\(t\)	точка
\ (t\) ">\(1\)	\((0.54, 0.84)\)
\ (t\) ">\(5\)	\((0.28, -0.96)\)
\ (t\) ">\(9\)	\((-0.91, 0.41)\)

	\((a)\)	\((b)\)	\((d)\)	\((i)\)	\((j)\)	\((l)\)	\((m)\)
\(t\)	\ (a)\)» клас = "lt-математика-17332">\(\dfrac{7\pi}{4}\)	\ (b)\)» клас = "lt-математика-17332">\(-\dfrac{7\pi}{4}\)	\ (d)\)» клас = "lt-математика-17332">\(-\dfrac{3\pi}{5}\)	\ (i)\)» клас = "lt-математика-17332">\(2.5\)	\ (j)\)» клас = "lt-математика-17332">\(-2.5\)	\ ((l)\)» клас = «lt-математика-17332">\(3 + 2\pi\)	\ (m)\)» клас = "lt-математика-17332">\(3 - \pi\)
Квадрант	\ (a)\)» Клас ="ЛТ-математика-17332">IV	\ (b)\)» Клас = "ЛТ-математика-17332">I	\ (d)\)» Клас = "ЛТ-математика-17332">III	\ (i)\)» Клас = "ЛТ-математика-17332">II	\ (j)\)» Клас ="ЛТ-математика-17332">III	\ (l)\)» Клас = "ЛТ-математика-17332">II	\ (m)\)» Клас ="ЛТ-математика-17332">IV

Довжина дуги на одиничному колі	Кінцева точка дуги	\(\cos(t)\)	\(\sin(t)\)
\(0\)	\((1, 0)\)	\(1\)	\(0\)
\(\dfrac{\pi}{2}\)
\(\pi\)
\(\dfrac{3\pi}{2}\)
\(2\pi\)

Довжина дуги на одиничному колі	Кінцева точка дуги	\(\cos(t)\)	\(\sin(t)\)
\(0\)	\((1, 0)\)	\(1\)	\(0\)
\(-\dfrac{\pi}{2}\)
\(-\pi\)
\(-\dfrac{3\pi}{2}\)
\(-2\pi\)

Довжина дуги на одиничному колі	Кінцева точка дуги	\(\cos(t)\)	\(\sin(t)\)
\(2\pi\)	\((1, 0)\)	\(1\)	\(0\)
\(\dfrac{5\pi}{2}\)
\(3\pi\)
\(\dfrac{7\pi}{2}\)
\(4\pi\)

\(t\)	\(\cot(t)\)	\(\sec(t)\)	\(\csc(t)\)
\(0\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{2}\)