11.8: Вектори

Як ми неодноразово бачили в цій книзі, математику можна використовувати для моделювання та вирішення реальних проблем. Для багатьох застосувань достатньо дійсних чисел; тобто дійсні числа з відповідними одиницями можна використовувати для відповіді на запитання на кшталт «Наскільки близько найближче гніздо Саскватча?» Є й інші часи, коли таких величин не вистачає. Можливо, важливо знати, наприклад, наскільки близько знаходиться найближче гніздо Саскватча, а також напрямок, в якому воно лежить. (Віщує використання підшипників у вправах, можливо?) Щоб відповісти на подібні запитання, які включають як кількісну відповідь, так і величину, разом з напрямком, ми використовуємо математичні об'єкти, які називаються векторами. ¹ Вектор представлений геометрично у вигляді спрямованого відрізка лінії, де величина вектора приймається довжиною відрізка лінії, а напрямок стає зрозумілим за допомогою стрілки в одній кінцевій точці відрізка. Звертаючись до векторів у цьому тексті, ми будемо приймати ² позначення «стрілка», тому символ$\vec{v}$ читається як «вектор»$v^{\prime}$. Нижче наведено типовий вектор$\vec{v}$ з кінцевими точками$P$ (1, 2) і$Q$ (4, 6). Точка$P$ називається початковою точкою або хвостом,$\vec{v}$ а точка$Q$ називається кінцевою точкою або головою$\vec{v}$. Оскільки ми можемо$\vec{v}$ повністю реконструювати з$P$ і$Q$$\vec{v}=\overrightarrow{P Q}$, пишемо, де важливий порядок точок$P$ (початкова точка) і$Q$ (кінцева точка). (Подумайте про це, перш ніж рухатися далі.)

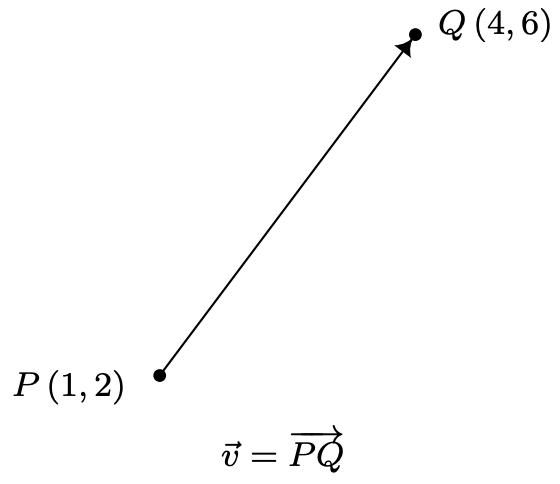
Хоча це правда, що$P$ і$Q$ повністю визначити$\vec{v}$, важливо зазначити, що оскільки вектори визначаються з точки зору їх двох характеристик, величини та напрямку, будь-який спрямований відрізок лінії з тією ж довжиною та напрямком, що і$\vec{v}$ вважається одним і тим же вектором як$\vec{v}$, незалежно від його початкової точки. У випадку нашого вектора$\vec{v}$ вище, будь-який вектор, який рухається на три одиниці вправо і чотири вгору ³ від початкової точки, щоб прийти до кінцевої точки, вважається тим самим вектором, що і$\vec{v}$. Позначення, яке ми використовуємо для захоплення цієї ідеї, є складовою формою вектора$\vec{v}=\langle 3,4\rangle$, де перше число, 3, називається$x$ -компонентом,$\vec{v}$ а друге число, 4, називається$y$ -компонентом$\vec{v}$. Якби ми хотіли реконструювати$\vec{v}=\langle 3,4\rangle$ з початковою точкою$P^{\prime}(-2,3)$, то ми б знайти кінцеву точку,$\vec{v}$ додавши 3 до$x$ -координати і додати 4 до$y$ -координати, щоб отримати кінцеву точку$Q^{\prime}(1,7)$, як показано нижче.

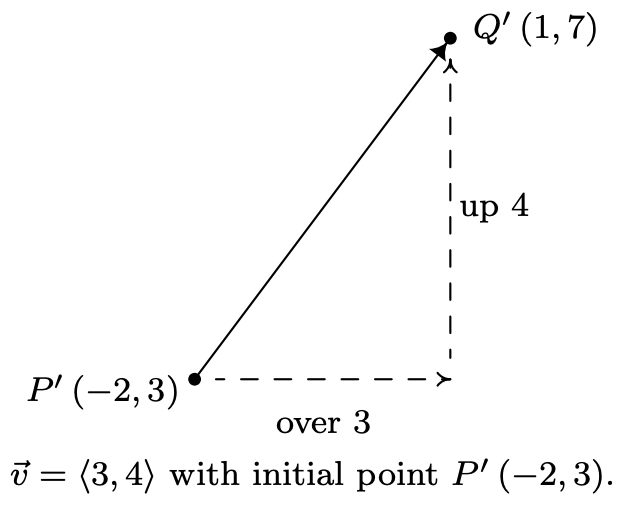
Компонентна форма вектора - це те, що пов'язує ці самі геометричні об'єкти назад до алгебри і, зрештою, тригонометрії. Узагальнюємо наш приклад у нашому визначенні нижче.

Визначення 11.5

Припустимо$\vec{v}$, представлений спрямованим відрізком лінії з початковою точкою$P\left(x_{0}, y_{0}\right)$ і кінцевою точкою$Q\left(x_{1}, y_{1}\right)$. Компонентна форма$\vec{v}$ задається

$$\vec{v}=\overrightarrow{P Q}=\left\langle x_{1}-x_{0}, y_{1}-y_{0}\right\rangle\nonumber$$

Використовуючи мову компонентів, ми маємо, що два вектори рівні тоді і тільки тоді, коли відповідні їх складові рівні. Тобто,$\left\langle v_{1}, v_{2}\right\rangle=\left\langle v_{1}^{\prime}, v_{2}^{\prime}\right\rangle$ якщо і тільки якщо$v_{1}=v_{1}^{\prime}$ і$v_{2}=v_{2}^{\prime}$. (Знову ж таки, подумайте про це, перш ніж читати далі.) Тепер ми встановимо про визначення операцій над векторами. Припустимо, нам дано два вектори$\vec{v}$ і$\vec{w}$. Сума, або результуючий вектор$\vec{v}+\vec{w}$ виходить наступним чином. По-перше, сюжет$\vec{v}$. Далі побудуйте$\vec{w}$ так, щоб його початкова точка була кінцевою точкою$\vec{v}$. Для побудови вектора$\vec{v}+\vec{w}$ ми починаємо в початковій точці$\vec{v}$ і закінчуємо в кінцевій точці$\vec{w}$. Корисно думати про вектор$\vec{v}+\vec{w}$ як про «чистий результат» руху уздовж,$\vec{v}$ а потім рухатися вздовж$\vec{w}$.

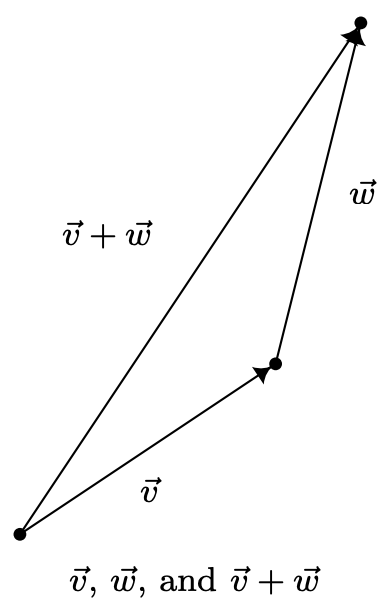
Наш наступний приклад добре використовує результуючі вектори та огляди підшипників та Закон Косинусів. ⁴

Приклад 11.8.1

Літак залишає аеропорт з повітряною швидкістю ⁵ 175 миль на годину на підшипнику$\mathrm{N} 40^{\circ} \mathrm{E}$. Вітер 35 милі на годину дме на підшипник$\mathrm{S} 60^{\circ} \mathrm{E}$. Знайдіть справжню швидкість літака, округлену до найближчої милі на годину, і справжню несучу площину, округлену до найближчого градуса.

Рішення

Як для площини, так і для вітру нам даються їх швидкості та напрямки. Швидкість зчеплення (як величина) з напрямком - це поняття швидкості, яке ми бачили кілька разів раніше в цьому підручнику. ⁶$\vec{v}$ Позначимо швидкість літака і$\vec{w}$ позначимо швидкість вітру на діаграмі нижче. «Справжня» швидкість і підшипник знаходять шляхом аналізу результуючого вектора,$\vec{v}+\vec{w}$. З векторної діаграми ми отримуємо трикутник, довжини сторін якого - величина$\vec{v}$, яка дорівнює 175, величина$\vec{w}$, яка дорівнює 35, і величина$\vec{v}+\vec{w}$, яку ми будемо називати$c$. З наведеної інформації підшипника ми йдемо по звичайній геометрії, щоб визначити, що кут між сторонами довжини 35 і 175 вимірює$100^{\circ}$.

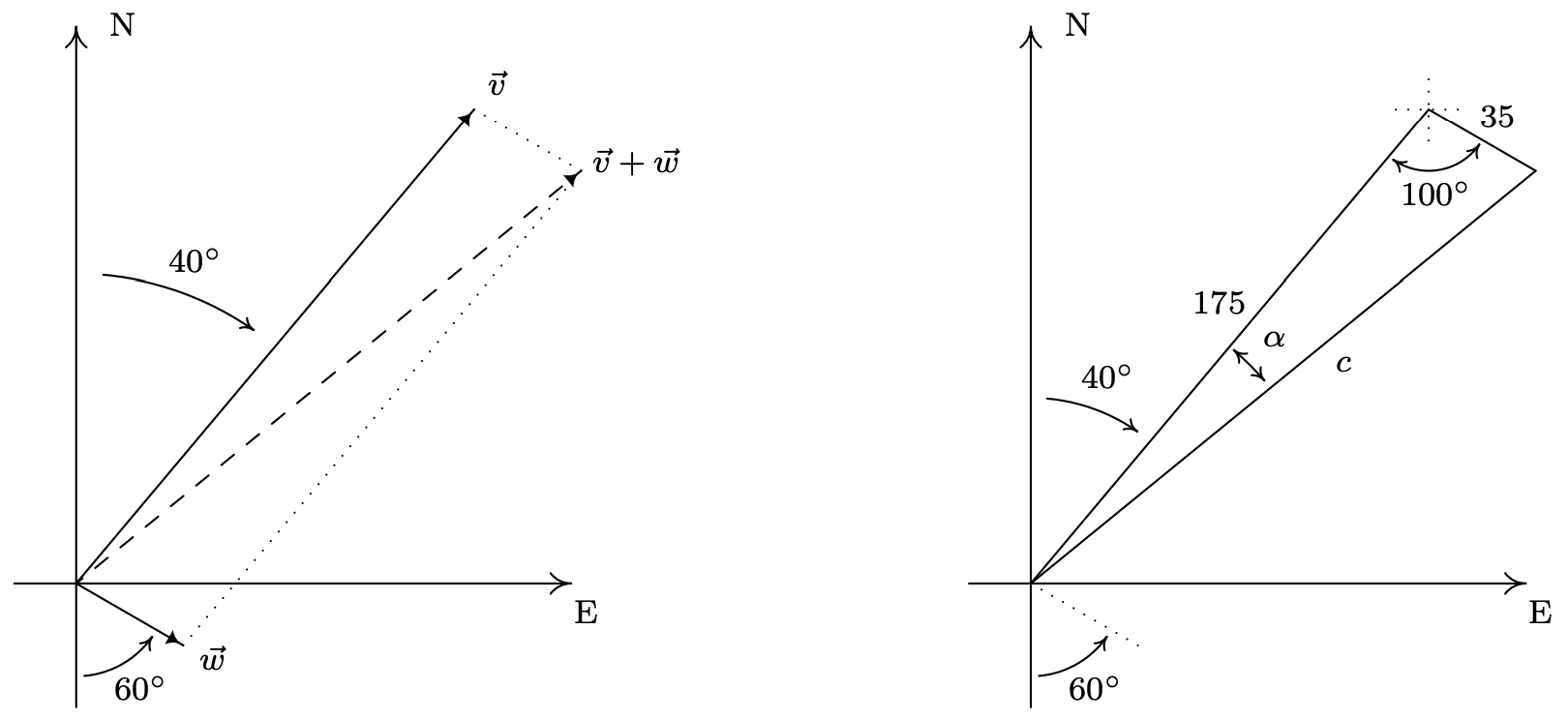
З Закону Косинуса ми визначимо$c=\sqrt{31850-12250 \cos \left(100^{\circ}\right)} \approx 184$, що означає справжня швидкість літака становить (приблизно) 184 милі на годину. Щоб визначити справжній підшипник площини, нам потрібно визначити кут$\alpha$. Використовуючи Закон Косинусів ще раз, ⁷ ми знаходимо$\cos (\alpha)=\frac{c^{2}+29400}{350 c}$ так$\alpha \approx 11^{\circ}$. З огляду на геометрію ситуації, додаємо$\alpha$ до заданого$40^{\circ}$ і знаходимо істинний підшипник площини, який повинен бути (приблизно)$\mathrm{N} 51^{\circ} \mathrm{E}$.

Наступним кроком є визначення додавання векторів покомпонентно, щоб відповідати геометричній дії. ⁸

Визначення 11.6

Припустимо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, і$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$. $\vec{v}+\vec{w}$Вектор визначається

$\vec{v}+\vec{w}=\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle$

Приклад 11.8.2

Нехай$\vec{v}=\langle 3,4\rangle$ і припустимо$\vec{w}=\overrightarrow{P Q}$, де$P(−3, 7)$ і$Q(−2, 5)$. Знайти$\vec{v}+\vec{w}$ і інтерпретувати цю суму геометрично.

Рішення

Перш ніж додати вектори за допомогою Definition 11.6, нам потрібно написати$\vec{w}$ у вигляді компонента. Використовуючи визначення 11.5, отримаємо$\vec{w}=\langle-2-(-3), 5-7\rangle=\langle 1,-2\rangle$. Таким чином

\ [\ почати {вирівняний}
\ vec {v} +\ vec {w} &=\ лангл 3,4\ діапазон+\ лангл 1, -2\ діапазон\\
&=\ кут 3+1,4+ (-2)\ діапазон\\
&=\ кут 4,2\ діапазон
\ кінець {вирівняний}\ nonumber\]

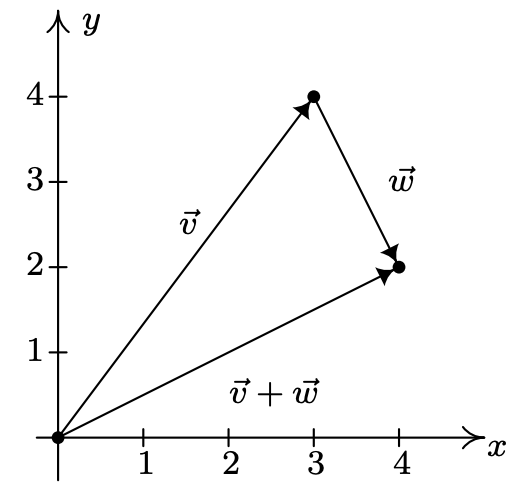
Щоб візуалізувати цю суму, малюємо$\vec{v}$ з її початковою точкою в (0, 0) (для зручності) так, щоб її кінцева точка була (3, 4). Далі проводимо графік$\vec{w}$ з його початковою точкою в (3, 4). Перемістивши одну вправо і дві вниз, знаходимо кінцеву точку$\vec{w}$ to be (4, 2). Ми бачимо, що вектор$\vec{v}+\vec{w}$ має початкову точку (0, 0) та кінцеву точку (4, 2), тому його складова форма$\langle 4,2\rangle$, як потрібно.

Для того, щоб векторне додавання користувалося тими ж властивостями, що і додавання дійсних чисел, необхідно розширити наше визначення векторів, включивши «нульовий вектор»,$\overrightarrow{0}=\langle 0,0\rangle$. Геометрично$\overrightarrow{0}$ являє собою точку, яку ми можемо розглядати як спрямований відрізок лінії з однаковими початковими та кінцевими точками. Читач цілком може заперечити проти включення$\overrightarrow{0}$, так як все-таки вектори повинні мати як величину (довжину), так і напрямок. Хоча здається зрозумілим, що величина$\overrightarrow{0}$ повинна бути 0, незрозуміло, який її напрямок. Як ми побачимо, напрямок насправді не визначено$\overrightarrow{0}$, але ця незначна гикавка в природному потоці речей варта переваг, які ми пожинаємо, включивши$\overrightarrow{0}$ в наші дискусії. У нас є наступна теорема.

Теорема 11.18. Властивості векторного додавання

• Комутативна властивість: Для всіх векторів$\vec{v}$ і$\vec{w}, \vec{v}+\vec{w}=\vec{w}+\vec{v}$.
• Асоціативна властивість: для всіх векторів$\vec{u}, \vec{v} \text { and } \vec{w},(\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})$.
• Властивість ідентичності: вектор$\overrightarrow{0}$ діє як адитивна ідентичність для векторного додавання. Тобто для всіх векторів$\vec{v}$, $$\vec{v}+\overrightarrow{0}=\overrightarrow{0}+\vec{v}=\vec{v}.\nonumber$$
• Зворотна властивість: Кожен вектор$\vec{v}$ має унікальну добавку, зворотну, позначену$-\vec{v}$. Тобто для кожного вектора$\vec{v}$ є свій вектор,$-\vec{v}$ щоб $$\vec{v}+(-\vec{v})=(-\vec{v})+\vec{v}=\overrightarrow{0}\nonumber$$

Властивості в теоремі 11.18 легко перевіряються за допомогою визначення векторного додавання. ⁹ Для комутативної власності відзначимо, що якщо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ і$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ тоді

$\begin{aligned} \vec{v}+\vec{w} &=\left\langle v_{1}, v_{2}\right\rangle+\left\langle w_{1}, w_{2}\right\rangle \\ &=\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle \\ &=\left\langle w_{1}+v_{1}, w_{2}+v_{2}\right\rangle \\ &=\vec{w}+\vec{v} \end{aligned}$

Геометрично ми можемо «побачити» комутативну властивість, розуміючи, що суми$\vec{v}+\vec{w}$ і$\vec{w}+\vec{v}$ є тією ж спрямованою діагоналлю, що визначається паралелограмом нижче.

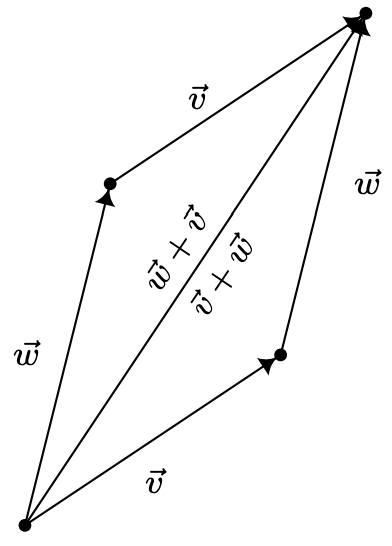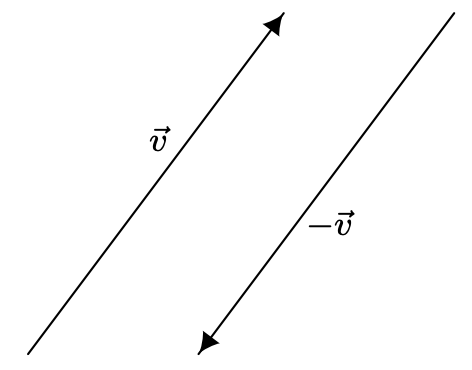
Демонстрація комутативної властивості векторного додавання.

Докази асоціативних і ідентичних властивостей протікають аналогічно, і читачеві рекомендується перевірити їх і надати супровідні діаграми. Існування і унікальність адитивної оберненої - це ще одна властивість, успадкована від дійсних чисел. Задано вектор$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, припустимо, що ми хочемо знайти вектор$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ так, що$\vec{v}+\vec{w}=\overrightarrow{0}$. За визначенням векторного додавання ми маємо$\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle=\langle 0,0\rangle$, а значить,$v_{1}+w_{1}=0$ і$v_{2}+w_{2}=0$. Дістаємо$w_{1}=-v_{1}$ і$w_{2}=-v_{2}$ так що$\vec{w}=\left\langle-v_{1},-v_{2}\right\rangle$. Значить,$\vec{v}$ має добавку зворотну, і більш того, вона унікальна і може бути отримана за формулою$-\vec{v}=\left\langle-v_{1},-v_{2}\right\rangle$. Геометрично вектори$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ і$-\vec{v}=\left\langle-v_{1},-v_{2}\right\rangle$ мають однакову довжину, але протилежні напрямки. В результаті, при геометричному складанні векторів сума$\vec{v}+(-\vec{v})$ призводить до того, що починається з початкової точки$\vec{v}$ і закінчується назад у початковій точці$\vec{v}$, або іншими словами, чистий результат переміщення$\vec{v}$ потім взагалі не$-\vec{v}$ рухається.

Використовуючи адитивну обернену вектора, ми можемо визначити різницю двох векторів,$\vec{v}-\vec{w}=\vec{v}+(-\vec{w})$. Якщо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ і$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ тоді

$\begin{aligned} \vec{v}-\vec{w} &=\vec{v}+(-\vec{w}) \\ &=\left\langle v_{1}, v_{2}\right\rangle+\left\langle-w_{1},-w_{2}\right\rangle \\ &=\left\langle v_{1}+\left(-w_{1}\right), v_{2}+\left(-w_{2}\right)\right\rangle \\ &=\left\langle v_{1}-w_{1}, v_{2}-w_{2}\right\rangle \end{aligned}$

Іншими словами, як і додавання векторів, векторне віднімання працює покомпонентно. Для інтерпретації вектора$\vec{v}-\vec{w}$ геометрично відзначимо

$\begin{array}{l} \vec{w}+(\vec{v}-\vec{w}) &=\vec{w}+(\vec{v}+(-\vec{w})) & \text { Definition of Vector Subtraction } \\ &=\vec{w}+((-\vec{w})+\vec{v}) & \text { Commutativity of Vector Addition } \\ &=(\vec{w}+(-\vec{w}))+\vec{v} & \text { Associativity of Vector Addition } \\ &=\overrightarrow{0}+\vec{v} & \text { Definition of Additive Inverse } \\ &=\vec{v} & \text { Definition of Additive Identity } \end{array}$

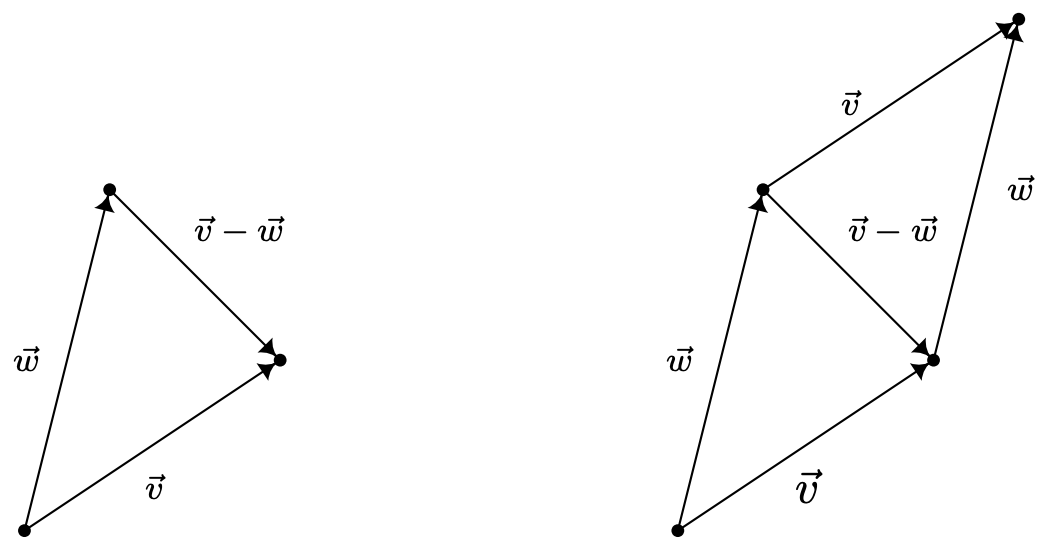
Це означає, що «чистий результат» руху вздовж,$\vec{w}$ а потім рухається вздовж$\vec{v}-\vec{w}$, є саме$\vec{v}$ собою. З наведеної нижче діаграми ми бачимо, що це$\vec{v}-\vec{w}$ можна інтерпретувати як вектор, початкова точка якого є кінцевою точкою$\vec{w}$ і кінцевою точкою якого є кінцева точка,$\vec{v}$ як показано нижче. Також варто згадати, що в паралелограмі визначається векторами$\vec{v}$ і$\vec{w}$, вектор$\vec{v}-\vec{w}$ є однією з діагоналей — інша істота$\vec{v}+\vec{w}$.

Далі ми обговорюємо скалярне множення — тобто прийняття дійсного числа разів вектора. Ми визначаємо скалярне множення для векторів так само, як ми визначили його для матриць у Розділі 8.3.

Визначення 11.7

Якщо$k$ є дійсним числом і$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, визначаємо$k \vec{v}$ по $$k \vec{v}=k\left\langle v_{1}, v_{2}\right\rangle=\left\langle k v_{1}, k v_{2}\right\rangle\nonumber$$

Скалярне множення$k$ на вектори можна розуміти геометрично як масштабування вектора (якщо$k > 0$) або масштабування вектора і зворотне його напрямок (якщо$k < 0$), як показано нижче.

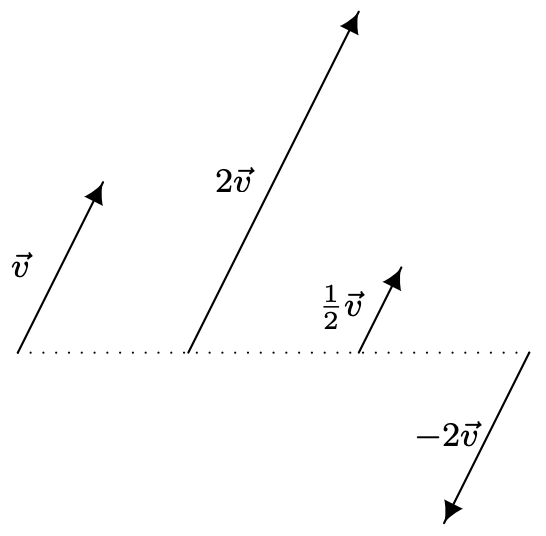
Зверніть увагу, що за визначенням 11.7,$(-1) \vec{v}=(-1)\left\langle v_{1}, v_{2}\right\rangle=\left\langle(-1) v_{1},(-1) v_{2}\right\rangle=\left\langle-v_{1},-v_{2}\right\rangle=-\vec{v}$. Це та інші властивості скалярного множення зведені нижче.

Теорема 11.19. Властивості скалярного множення

• Асоціативна властивість: Для кожного вектора$\vec{v}$ і скалярів$k$ і$r$,$(k r) \vec{v}=k(r \vec{v})$.
• Властивість ідентичності: Для всіх векторів$\vec{v}, 1 \vec{v}=\vec{v}$.
• Адитивна зворотна властивість: Для всіх векторів$\vec{v},-\vec{v}=(-1) \vec{v}$.
• Розподільна властивість скалярного множення через скалярне додавання: для кожного вектора$\vec{v}$ та скалярів$k$ та$r$, $$(k+r) \vec{v}=k \vec{v}+r \vec{v}\nonumber$$
• Розподільна властивість скалярного множення над векторним додаванням: Для всіх векторів$\vec{v}$$\vec{w}$ та$k$ скалярів $$k(\vec{v}+\vec{w})=k \vec{v}+k \vec{w}\nonumber$$
• нульовий продукт властивості: якщо$\vec{v}$ вектор і$k$ є скалярним, то $$k \vec{v}=\overrightarrow{0} \quad \text { if and only if } \quad k=0 \quad \text { or } \quad \vec{v}=\overrightarrow{0}\nonumber$$

Доказ теореми 11.19, як і доказ теореми 11.18, зрештою зводиться до визначення скалярного множення і властивостей дійсних чисел. Наприклад, щоб довести асоціативне властивість, дозволимо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. Якщо$k$ і$r$ є скалярами, то

$\begin{aligned} (k r) \vec{v} &=(k r)\left\langle v_{1}, v_{2}\right\rangle & & \\ &=\left\langle(k r) v_{1},(k r) v_{2}\right\rangle & & \text { Definition of Scalar Multiplication } \\ &=\left\langle k\left(r v_{1}\right), k\left(r v_{2}\right)\right\rangle & & \text { Associative Property of Real Number Multiplication } \\ &=k\left\langle r v_{1}, r v_{2}\right\rangle & & \text { Definition of Scalar Multiplication } \\ &=k\left(r\left\langle v_{1}, v_{2}\right\rangle\right) & & \text { Definition of Scalar Multiplication } \\ &=k(r \vec{v}) & & \end{aligned}$

Решта властивості доводяться аналогічно і залишаються як вправи.

Наш наступний приклад демонструє, як Теорема 11.19 дозволяє нам робити такі ж алгебраїчні маніпуляції з векторами, як і зі змінними - множення і ділення векторів незалежно від. Якщо педантизм здається знайомим, слід. Це те саме лікування, яке ми дали приклад 8.3.1 в розділі 8.3. Як і в цьому прикладі, ми детально описуємо рішення, щоб спонукати читача добре подумати, чому кожен крок виправданий.

Приклад 11.8.3

Вирішити$5 \vec{v}-2(\vec{v}+\langle 1,-2\rangle)=\overrightarrow{0} \text { for } \vec{v}$.

Рішення

\ (\ почати {вирівняний}
5\ vec {v} -2 (\ vec {v} +\ кут 1, -2\ діапазон) &=\ переправа стрілка {0}\\
5\ vec {v} + (-1) [2 (\ vec {v} +\ кут 1, -2\ діапазон)] &=\ переправа стрілка {0}\\
5\ vec {v} + (-1) (2)] (\ vec {v} +\ кут 1, -2\ діапазон) &=\ переправа стрілка {0}\\
5\ vec {v} + (-2) ( \ vec {v} +\ кут 1, -2\ діапазон) &=\ переправа стрілка {0}\\
5\ vec {v} + [(-2)\ vec {v} + (-2)\ кут 1, -2\ діапазон] &=\ переправо {0}\
5\ vec {v} + [(-2)\ vec {v} +\ vec {v} +\ langle (-2) 1), (-2) (-2)\ діапазон] &=\ переправа стрілка {0}\\
{[5\ vec {v} + (-2)\ vec {v}] +\ langle-2,4\ діапазон} & ; =\ переправа стрілка {0}\\
(5+ (-2))\ vec {v} +\ лангу-2,4\ діапазон &=\ переправа стрілка {0}\\
3\ vec {v} +\ langle-2,4\ діапазон &=\ переправа стрілка {0}\\
(3\ vec {v} +\ langle-2,4\ діапазон) + (\\ le-2,4\ діапазон) &=\ переправа стрілка {0} + (-\ langle-2,4\ діапазон)\\
3\ vec {v} + [\ ланг-2,4\ діапазон+ (-\ ланг-2,4\ діапазон)] &=\ переправа стрілка {0} + (-1)\ ланг-2,4\ діапазон\\
3\ vec {v} +\ переправа стрілка {0} &=\ переправо {0} +\ langle (-1) (-2), (-1), (-1) (4) діапазон\\
3\ vec {v} &=\ лангл 2, -4\ діапазон\\
\ гідророзриву {1} {3} (3\ vec {v}) &=\ FRAC {1} { 3} (\ кут 2, -4\ діапазон)\\
{\ лівий [\ лівий (\ frac {1} {3}\ праворуч) (3)\ праворуч]\ vec {v}} &=\ ліворуч\ лангіт\ ліворуч (\ frac {1} {1} {1}\ правий) (2),\ лівий (\ frac {1} {3}\ правий) (-4)\ правий) (2),\ лівий (\ frac {
1}\ правий) (-4)\\ 1\ vec {v} &=\ лівий\ лангель\ frac {2} {3}, -\ frac {4} {3}\ правий\ діапазон
\\ vec {v} &=\ лівий\ лангл\ гідророзриву {2} {3}, -\ гідророзриву {4} {3}\ праворуч\ діапазон
\ кінець {вирівняний}\)

Вектор, початкова точка якого (0, 0), як кажуть, знаходиться в стандартному положенні. Якщо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ наноситься в стандартному положенні, то його кінцева точка необхідна$\left(v_{1}, v_{2}\right)$. (Ще раз подумайте про це, перш ніж читати далі.)

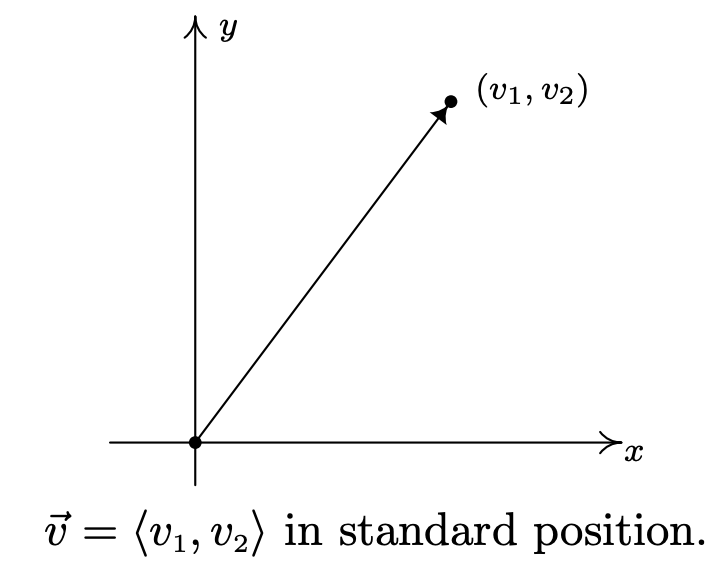
Побудова вектора в стандартному положенні дозволяє нам легше кількісно оцінити поняття величини і напрямку вектора. Ми можемо перетворити точку$\left(v_{1}, v_{2}\right)$ в прямокутних координатах в пару$(r, \theta)$ в полярних координатах де$r \geq 0$. Величина$\vec{v}$, про яку ми говорили раніше, була довжиною спрямованого відрізка лінії, є$r=\sqrt{v_{1}^{2}+v_{2}^{2}}$ і позначається$\|\vec{v}\|$. З розділу 11.4 ми знаємо$v_{1}=r \cos (\theta)=\|\vec{v}\| \cos (\theta)$ і$v_{2}=r \sin (\theta)=\|\vec{v}\| \sin (\theta)$. З визначення скалярного множення і векторної рівності отримаємо

$\begin{aligned} \vec{v} &=\left\langle v_{1}, v_{2}\right\rangle \\ &=\langle\|\vec{v}\| \cos (\theta),\|\vec{v}\| \sin (\theta)\rangle \\ &=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle \end{aligned}$

Це мотивує наступне визначення.

Визначення 11.8

Припустимо,$\vec{v}$ це вектор з формою компонента$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. $(r, \theta)$Дозволяти полярне подання точки з прямокутними координатами$\left(v_{1}, v_{2}\right)$ с$r \geq 0$.

• Величина$\vec{v}$, що позначається$\|\vec{v}\|$, задається$\|\vec{v}\|=r=\sqrt{v_{1}^{2}+v_{2}^{2}}$
• Якщо$\vec{v} \neq \overrightarrow{0}$, (вектор) напрямок$\vec{v}$,$\hat{v}$ що позначається, задається$\hat{v}=\langle\cos (\theta), \sin (\theta)\rangle$

Взяті разом, отримуємо$\vec{v}=\langle\|\vec{v}\| \cos (\theta),\|\vec{v}\| \sin (\theta)\rangle$.

Кілька зауважень по порядку. По-перше, ми зауважимо, що якщо$\vec{v} \neq 0$ тоді, хоча існує нескінченно багато кутів,$\theta$ які задовольняють Визначенню 11.8,$r > 0$ умова означає, що всі кути є співтермінальними. Отже, якщо$\theta$ і$\theta^{\prime}$ обидва задовольняють умовам визначення 11.8, то$\cos (\theta)=\cos \left(\theta^{\prime}\right)$ і$\sin (\theta)=\sin \left(\theta^{\prime}\right)$, і як таке,$\langle\cos (\theta), \sin (\theta)\rangle=\left\langle\cos \left(\theta^{\prime}\right), \sin \left(\theta^{\prime}\right)\right\rangle$ внесення$\hat{v}$ чітко визначено. ¹⁰ Якщо$\vec{v}=\overrightarrow{0}$, то$\vec{v}=\langle 0,0\rangle$, і ми знаємо з розділу 11.4, що$(0, \theta)$ є полярним представленням для початку для будь-якого кута$\theta$. З цієї причини,$\hat{0}$ не визначено. Наступна теорема узагальнює важливі факти про величину та напрямок вектора.

Теорема 11.20. Властивості величини та напряму

Припустимо,$\vec{v}$ це вектор.

• $\|\vec{v}\| \geq 0$і$\|\vec{v}\|=0$ якщо і тільки якщо$\vec{v}=\overrightarrow{0}$
• Для всіх скалярів$k$,$\|k \vec{v}\|=|k|\|\vec{v}\|$.
• Якщо$\vec{v} \neq \overrightarrow{0}$ тоді$\vec{v}=\|\vec{v}\| \hat{v}$, так що$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$.

Доказ першої властивості в теоремі 11.20 є прямим наслідком визначення$\|\vec{v}\|$. Якщо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, то$\|\vec{v}\|=\sqrt{v_{1}^{2}+v_{2}^{2}}$ який за визначенням більше або дорівнює 0. Причому,$\sqrt{v_{1}^{2}+v_{2}^{2}}=0$ якщо і тільки$v_{1}^{2}+v_{2}^{2}=0$ якщо і тільки якщо$v_{1}=v_{2}=0$. Значить,$\|\vec{v}\|=0$ якщо і тільки тоді$\vec{v}=\langle 0,0\rangle=\overrightarrow{0}$, як потрібно.

Друга властивість є результатом визначення величини і скалярного множення поряд зі властивістю радикалів. Якщо$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ і$k$ є скаляром, то

$\begin{aligned} \|k \vec{v}\| &=\left\|k\left\langle v_{1}, v_{2}\right\rangle\right\| & & \\ &=\left\|\left\langle k v_{1}, k v_{2}\right\rangle\right\| & & \text { Definition of scalar multiplication } \\ &=\sqrt{\left(k v_{1}\right)^{2}+\left(k v_{2}\right)^{2}} & & \text { Definition of magnitude } \\ &=\sqrt{k^{2} v_{1}^{2}+k^{2} v_{2}^{2}} & & \\ &=\sqrt{k^{2}\left(v_{1}^{2}+v_{2}^{2}\right)} & & \\ &=\sqrt{k^{2}} \sqrt{v_{1}^{2}+v_{2}^{2}} & & \text { Product Rule for Radicals } \\ &=|k| \sqrt{v_{1}^{2}+v_{2}^{2}} & & \text { Since } \sqrt{k^{2}}=|k| \\ &=|k|\|\vec{v}\| & & \end{aligned}$

Рівняння$\vec{v}=\|\vec{v}\| \hat{v}$ в теоремі 11.20 є наслідком визначень$\|\vec{v}\|$$\hat{v}$ і було розроблено в обговоренні безпосередньо перед визначенням 11.8 на сторінці 1020. У словах рівняння$\vec{v}=\|\vec{v}\| \hat{v}$ говорить про те, що будь-який заданий вектор є добутком його величини і його напрямку — важливе поняття, про яке слід пам'ятати при вивченні та використанні векторів. Рівняння$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$ є результатом розв'язання$\vec{v}=\|\vec{v}\| \hat{v}$ для$\hat{v}$ шляхом множення ¹¹ обох сторін рівняння на$\frac{1}{\|\vec{v}\|}$ і використання властивостей теореми 11.19. Ми прострочені для прикладу.

Приклад 11.8.4

1. Знайти складову форму вектора$\vec{v}$ з$\|\vec{v}\|=5$ таким чином, щоб при$\vec{v}$ побудові в стандартному положенні він лежав у квадранті II і утворював$60^{\circ}$ кут ¹² з негативною віссю x.
2. Для$\vec{v}=\langle 3,-3 \sqrt{3}\rangle$, знайти$\|\vec{v}\|$ і$\theta$,$0 \leq \theta<2 \pi$ щоб$\vec{v}=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle$.
3. Для векторів$\vec{v}=\langle 3,4\rangle$ і$\vec{w}=\langle 1,-2\rangle$, знайдіть наступне.
   1. $\hat{v}$
   2. $\|\vec{v}\|-2\|\vec{w}\|$
   3. $\|\vec{v}-2 \vec{w}\|$
   4. $\|\hat{w}\|$

Рішення

1. Нам кажуть, що$\|\vec{v}\|=5$ і дається інформація про його напрямок, тому ми можемо використовувати формулу$\vec{v}=\|\vec{v}\| \hat{v}$ для отримання складової форми$\vec{v}$. Для визначення$\hat{v}$ звертаємося до визначення 11.8. Нам кажуть, що$\vec{v}$ лежить в квадранті II і робить$60^{\circ}$ кут з негативною$x$ -віссю, тому полярна форма кінцевої точки$\vec{v}$, при побудові в стандартному положенні є$\left(5,120^{\circ}\right)$. (Див. Схему нижче.) Таким чином$\hat{v}=\left\langle\cos \left(120^{\circ}\right), \sin \left(120^{\circ}\right)\right\rangle=\left\langle-\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle, \text { so } \vec{v}=\|\vec{v}\| \hat{v}=5\left\langle-\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle=\left\langle-\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right\rangle$.

   

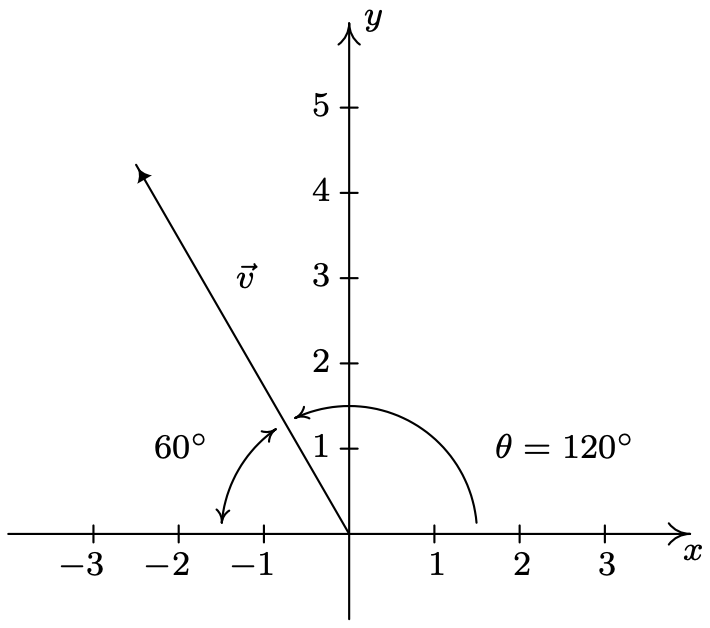
2. За$\vec{v}=\langle 3,-3 \sqrt{3}\rangle$, отримуємо$\|\vec{v}\|=\sqrt{(3)^{2}+(-3 \sqrt{3})^{2}}=6$. У світлі визначення 11.8, ми можемо знайти$\theta$ ми після перетворення точки з прямокутними координатами$(3,-3 \sqrt{3})$ в полярну форму$(r, \theta)$ де$r=\|\vec{v}\|>0$. З розділу 11.4 ми маємо$\tan (\theta)=\frac{-3 \sqrt{3}}{3}=-\sqrt{3}$. Оскільки$(3,-3 \sqrt{3})$ є точкою в квадранті IV,$\theta$ є кутом квадранта IV. Значить, підбираємо$\theta=\frac{5 \pi}{3}$. Ми можемо перевірити нашу відповідь, перевіривши$\vec{v}=\langle 3,-3 \sqrt{3}\rangle=6\left\langle\cos \left(\frac{5 \pi}{3}\right), \sin \left(\frac{5 \pi}{3}\right)\right\rangle$.
3. 1. Оскільки нам дається складова форма$\vec{v}$, ми будемо використовувати формулу$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$. Бо$\vec{v}=\langle 3,4\rangle$, у нас є$\|\vec{v}\|=\sqrt{3^{2}+4^{2}}=\sqrt{25}=5$. Отже,$\hat{v}=\frac{1}{5}\langle 3,4\rangle=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle$.
   2. Ми знаємо з нашої роботи вище$\|\vec{v}\|=5$, що, тому, щоб знайти$\|\vec{v}\|-2\|\vec{w}\|$, нам потрібно тільки знайти$\|\vec{w}\|$. З тих пір$\vec{w}=\langle 1,-2\rangle$, ми отримуємо$\|\vec{w}\|=\sqrt{1^{2}+(-2)^{2}}=\sqrt{5}$. Отже,$\|\vec{v}\|-2\|\vec{w}\|=5-2 \sqrt{5}$.
   3. У виразі зверніть увагу$\|\vec{v}-2 \vec{w}\|$, що спочатку йде арифметика на векторах, потім величина. Отже, наш перший крок - знайти складову форму вектора$\vec{v}-2 \vec{w}$. Отримуємо$\vec{v}-2 \vec{w}=\langle 3,4\rangle-2\langle 1,-2\rangle=\langle 1,8\rangle$. Отже,$\|\vec{v}-2 \vec{w}\|=\|\langle 1,8\rangle\|=\sqrt{1^{2}+8^{2}}=\sqrt{65}$.
   4. Щоб знайти$\|\hat{w}\|$, нам спочатку потрібно$\hat{w}$. Використовуючи$\hat{w}=\left(\frac{1}{\|\vec{w}\|}\right) \vec{w}$ разом з формулою$\|\vec{w}\|=\sqrt{5}$, яку ми знайшли в попередній задачі, отримуємо$\hat{w}=\frac{1}{\sqrt{5}}\langle 1,-2\rangle=\left\langle\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}}\right\rangle=\left\langle\frac{\sqrt{5}}{5},-\frac{2 \sqrt{5}}{5}\right\rangle$. Отже,$\|\hat{w}\|=\sqrt{\left(\frac{\sqrt{5}}{5}\right)^{2}+\left(-\frac{2 \sqrt{5}}{5}\right)^{2}}=\sqrt{\frac{5}{25}+\frac{20}{25}}=\sqrt{1}=1$.

Процес на прикладі № 1 у прикладі 11.8.4 вище, за допомогою якого ми беремо інформацію про величину і напрямок вектора і знаходимо складову форму вектора, називається розв'язанням вектора на його складові. Як застосування цього процесу, ми переглядаємо приклад 11.8.1 нижче.

Приклад 11.8.5

Літак залишає аеропорт зі швидкістю 175 миль на годину з підшипником$\mathrm{N} 40^{\circ} \mathrm{E}$. Вітер 35 милі на годину дме на підшипник$\mathrm{S} 60^{\circ} \mathrm{E}$. Знайдіть справжню швидкість літака, округлену до найближчої милі на годину, і справжню несучу площину, округлену до найближчого градуса.

Рішення

Ми продовжуємо, як ми зробили в прикладі 11.8.1 і давайте$\vec{v}$$\vec{w}$ позначити швидкість літака і позначити швидкість вітру, і встановити про визначення$\vec{v}+\vec{w}$. Якщо ми розглядаємо аеропорт як на початку, позитивна$y$ -вісь діє як належна північ, а позитивна$x$ -вісь діє як належний схід, ми бачимо, що вектори$\vec{v}$ і$\vec{w}$ знаходяться в стандартному положенні та їх напрямки відповідають кутам$50^{\circ}$ і$-30^{\circ}$, відповідно. Отже, складова форма$\vec{v}=175\left\langle\cos \left(50^{\circ}\right), \sin \left(50^{\circ}\right)\right\rangle=\left\langle 175 \cos \left(50^{\circ}\right), 175 \sin \left(50^{\circ}\right)\right\rangle$ і складова форма$\vec{w}=\left\langle 35 \cos \left(-30^{\circ}\right), 35 \sin \left(-30^{\circ}\right)\right\rangle$. Оскільки у нас немає зручного способу вираження точних значень косинуса і синуса$50^{\circ}$, ми залишаємо обидва вектора через косинуси і синуси. ¹³ Додавши відповідні компоненти, знаходимо результуючий вектор$\vec{v}+\vec{w}=\left\langle 175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right), 175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right\rangle$. Щоб знайти «справжню» швидкість літака, ми обчислюємо величину цього результуючого вектора $$\|\vec{v}+\vec{w}\|=\sqrt{\left(175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right)\right)^{2}+\left(175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right)^{2}} \approx 184\nonumber$$ Отже, «справжня» швидкість літака становить приблизно 184 милі на годину. Щоб знайти справжній підшипник, нам потрібно знайти кут$(r, \theta), r>0$,$\theta$ який відповідає полярній формі точки$(x, y)=\left(175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right), 175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right)$. Оскільки обидві ці координати є позитивними, ¹⁴ ми знаємо,$\theta$ є кутом квадранта I, як показано нижче. Крім того, $$\tan (\theta)=\frac{y}{x}=\frac{175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)}{175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right)},\nonumber$$ таким чином, використовуючи функцію арктангенс, ми отримуємо$\theta \approx 39^{\circ}$. Оскільки для цілей підшипника нам потрібен кут між$\vec{v}+\vec{w}$ і позитивною$y$ -віссю, ми беремо доповнення$\theta$ і знаходимо «істинний» підшипник площини приблизно$\mathrm{N} 51^{\circ} \mathrm{E}$.

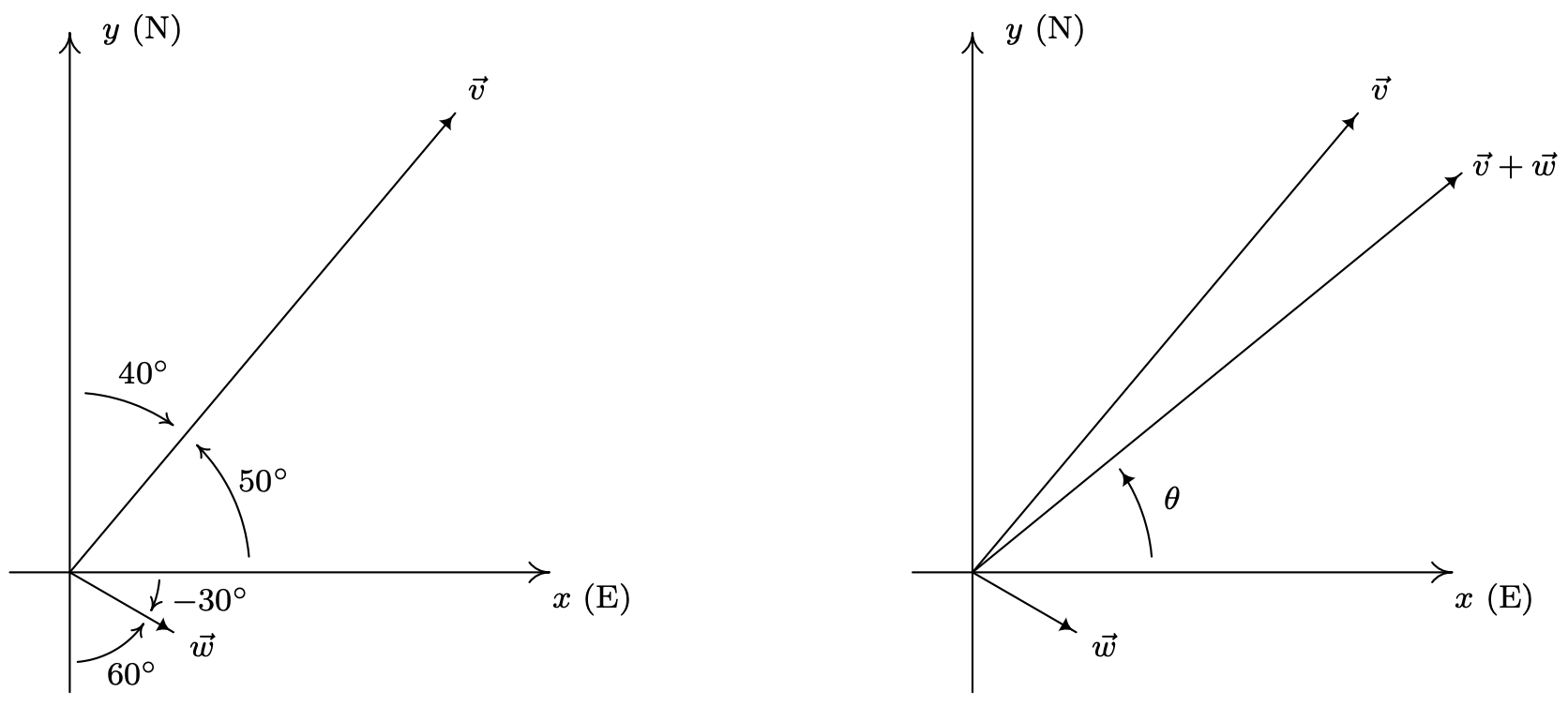
У частині 3d Приклад 11.8.4, ми побачили, що$\|\hat{w}\|=1$. Вектори довжиною 1 мають особливу назву і важливі в нашому подальшому вивченні векторів.

Визначення 11.9

Одиниці векторів:$\vec{v}$ Дозволяти бути вектором. Якщо$\|\vec{v}\|=1$, ми говоримо, що$\vec{v}$ це одиничний вектор.

Якщо$\vec{v}$ це одиничний вектор, то обов'язково,$\vec{v}=\|\vec{v}\| \hat{v}=1 \cdot \hat{v}=\hat{v}$. І навпаки, ми залишаємо це як вправу ¹⁵, щоб показати, що$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$ це одиничний вектор для будь-якого ненульового вектора$\vec{v}$. На практиці, якщо$\vec{v}$ це одиничний вектор, ми пишемо його на$\vec{v}$ відміну від$\vec{v}$ тому, що ми зарезервували позначення «» для одиничних векторів. Процес множення ненульового вектора на коефіцієнт$\frac{1}{\|\vec{v}\|}$ для отримання одиничного вектора називається «нормалізацією вектора», а отриманий вектор$\vec{v}$ називається «одиничним вектором у напрямку$\vec{v^{\prime}}$. Кінцеві точки одиничних векторів при нанесенні в стандартному положенні лежать на Одиничному колі. (Ви повинні витратити час, щоб показати це.) В результаті ми візуалізуємо нормалізацію ненульового вектора$\vec{v}$ як стиснення ¹⁶ його кінцевої точки, при нанесенні в стандартному положенні, назад до одиничного кола.

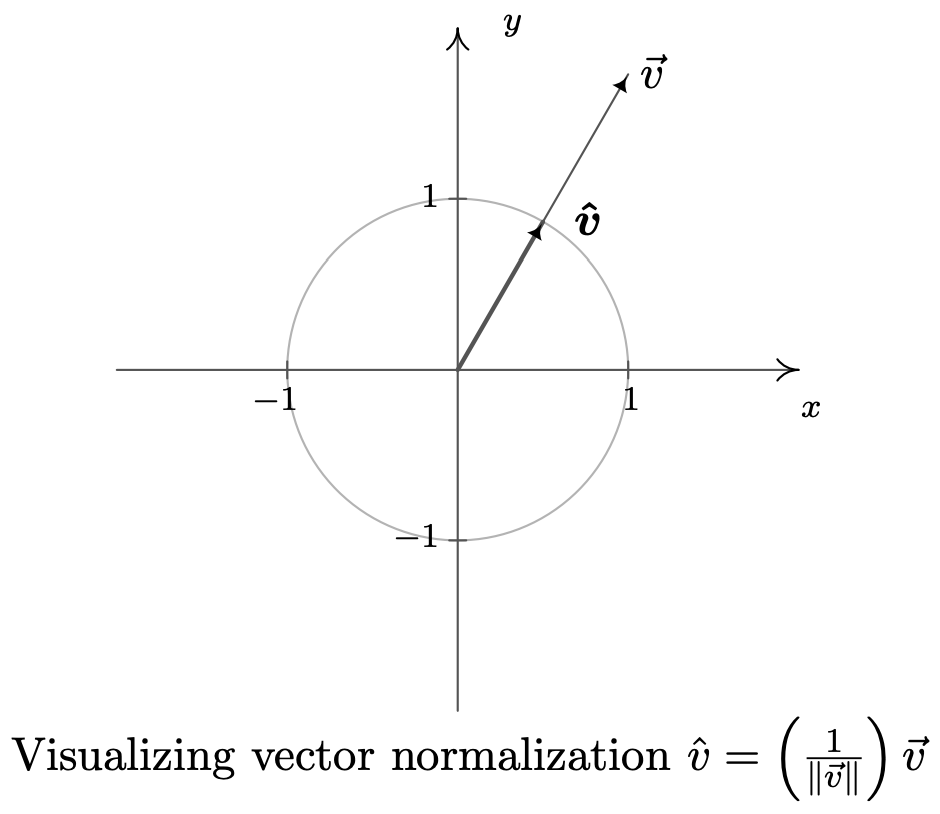
З усіх векторів одиниць два заслуговують окремої згадки.

Визначення 11.10. Вектори основних одиниць

• $\hat{\imath}$Вектор визначається$\hat{\imath}=\langle 1,0\rangle$
• $\hat{\jmath}$Вектор визначається$\hat{\imath}=\langle 0,1\rangle$

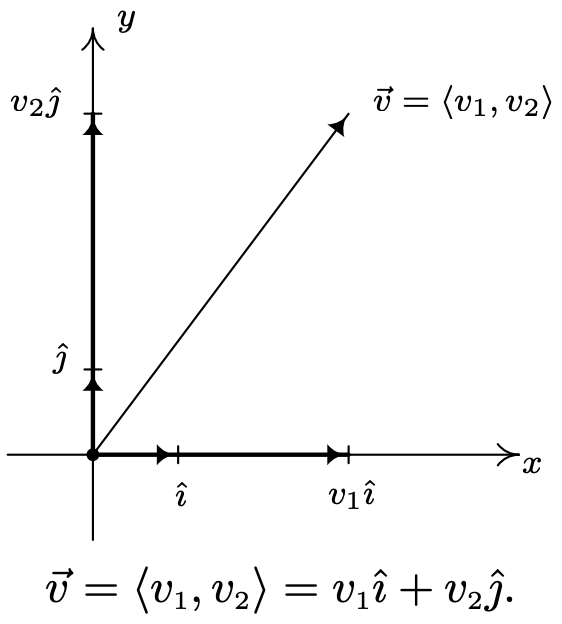
Ми можемо думати про вектор$\hat{\imath}$ як представлення позитивного$x$ напрямку, тоді як$\hat{\jmath}$ представляє позитивний$y$ -напрямок. У нас є наступна теорема про розкладання. ¹⁷

Теорема 11.21. Теорема про розкладання головного вектора

$\vec{v}$Дозволяти вектор з формою компонента$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. Потім$\vec{v}=v_{1} \hat{\imath}+v_{2} \hat{\jmath}$.

Доказ теореми 11.21 є простим. Оскільки$\hat{\imath}=\langle 1,0\rangle$ і$\hat{\jmath}=\langle 0,1\rangle$, ми маємо з визначення скалярного множення та додавання векторів, що

$v_{1} \hat{\imath}+v_{2} \hat{\jmath}=v_{1}\langle 1,0\rangle+v_{2}\langle 0,1\rangle=\left\langle v_{1}, 0\right\rangle+\left\langle 0, v_{2}\right\rangle=\left\langle v_{1}, v_{2}\right\rangle=\vec{v}$

Геометрично ситуація виглядає наступним чином:

Завершуємо цей розділ класичним прикладом, який демонструє, як вектори використовуються для моделювання сил. «Сила» визначається як «поштовх» або «тягнути». Інтенсивність поштовху або тяги - це величина сили, і вимірюється в Netwons (N) в системі SI або фунтах (фунтів.) в англійській системі. ¹⁸ Наступний приклад використовує всі поняття в цьому розділі, і його слід вивчити дуже докладно.

Приклад 11.8.6

50-фунтовий динамік підвішений до стелі двома опорними скобами. Якщо один з них робить$60^{\circ}$ кут зі стелею, а інший робить$30^{\circ}$ кут зі стелею, які натяги на кожній з опор?

Рішення

Представляємо задачу схематично нижче, а потім наводимо відповідну векторну діаграму.

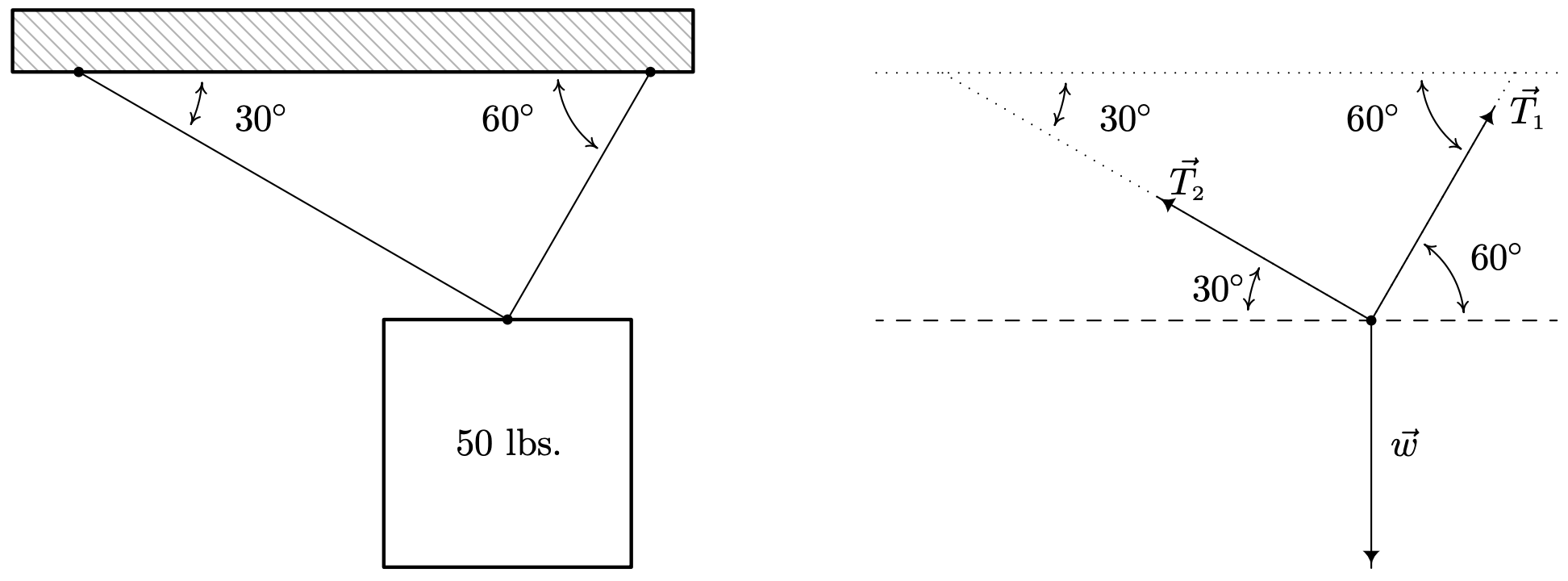
У нас на динамік діють три сили: вага динаміка, який ми будемо називати$\vec{w}$, тягнучи динамік прямо вниз, і сили на опорні стрижні, які ми будемо називати$\vec{T}_{1}$ і$\vec{T}_{2}$ (для «напружень»)$30^{\circ}$, що діють вгору під кутами$60^{\circ}$ і відповідно. Ми шукаємо напруженість на опорі, які є величинами$\left\|\vec{T}_{1}\right\|$ і$\left\|\vec{T}_{2}\right\|$. Для того щоб динамік залишався нерухомим, потрібно ¹⁹$\vec{w}+\overrightarrow{T_{1}}+\overrightarrow{T_{2}}=\overrightarrow{0}$. Розглядаючи загальну початкову точку цих векторів як початок і пунктирну лінію як$x$ вісь -, ми використовуємо теорему 11.20, щоб отримати компонентні зображення для трьох задіяних векторів. Ми можемо моделювати вагу динаміка як вектор, спрямований безпосередньо вниз з величиною 50 фунтів. Тобто,$\|\vec{w}\|=50$ і$\hat{w}=-\hat{\jmath}=\langle 0,-1\rangle$. Отже,$\vec{w}=50\langle 0,-1\rangle=\langle 0,-50\rangle$. За силу в першій опорі отримуємо\ [\ begin {вирівняний}
\ vec {T} _ {1} &=\ лівий\ |\ vec {T} _ {1}\ правий\ |\ лівий\ лангл\ cos\ left (60^ {\ circ}\ правий)\ sin\ left (60^ {\ circ}\ праворуч)\ правий\ діапазон\\ &=\ лівий\ lкут\ frac {\ лівий\ |\ vec {T} _ {1}\ право\ |} {2},\ frac {\ лівий\ |\ vec {T} _ {1}\ вправо\ |\ sqrt {3}} {2}\ right\ rangle\ end {aligned}\ nonumber\] Для другої опори зауважимо, що кут$30^{\circ}$ вимірюється від негативної$x$ -осі, тому кут, необхідний для запису$\overrightarrow{T_{2}}$ у вигляді компонента, є$150^{\circ}$. Звідси\ [\ почати {вирівняний}\ vec {T} _ {2} &=\ лівий\ |\ vec {T} _ {2}\ вправо\ |\ лівий\ лангл\ cos\ лівий (150^ {\ circ}\ правий),\ sin\ лівий (150^ {\ circ}\ вправо\ діапазон\\ &=\ лівий\ langle-\ frac {\ лівий\ |\ vec {T} _ {2}\ право\ |\ sqrt {3}} {2},\ frac {\ лівий\ |\ vec {T} _ {2}\ праворуч\ |} {2}\ праворуч\ діапазон
\ кінець {вирівняний}\] вимога$\vec{w}+\vec{T}_{1}+\vec{T}_{2}=\overrightarrow{0}$ дає нам це векторне рівняння. \ [\ begin {масив} {rrl}
&\ vec {w} +\ vec {T} _ {1} +\ vec {T} _ {2} &= &\ overrightarrow {0}\ &\ langle 0, -50\\ діапазон\ ліворуч\\ frac {\ лівий\ |\ vec {T} _ {1}\ вправо\} | {2},\ frac {\ лівий\ |\ vec {T} _ {1}\ вправо\ |\ sqrt {3}} {2}\ праворуч\ діапазон+\ лівий\ ланґль-\ frac {\ лівий\ |\ vec {T} _ {2}\ вправо\ |\ sqrt {3}} {2},\ frac {\ лівий\ |\ vec {T} _ {2}\ праворуч\ |} {2}\ праворуч\ діапазон&= &\ кут 0,0\ діапазон\\ &\ лівий\ кут\ frac {\ лівий\ |\ vec {T} _ {1}\ вправо\ |} {2} -\ frac {\ ліворуч\ |\ vec {T} _ {2}\ вправо |\ sqrt {3} {2},\ frac {\ ліворуч\ |\ vec {T} _ {1}\ праворуч\ |\ sqrt {3}} {2} +\ лівий\ |\ vec {T} _ {2}\ вправо\ |} {2} -50\ правий\ діапазон = &\ langle 0,0\ кінець {масив}\ nonumber\] Прирівнюючи відповідні складові векторів з кожного боку, отримаємо систему лінійних рівнянь в змінних$\left\|\overrightarrow{T_{1}}\right\|$ і$\left\|\vec{T}_{2}\right\|$. $$\left\{\begin{array}{l} (E 1) \quad \frac{\left\|\vec{T}_{1}\right\|}{2}-\frac{\left\|\vec{T}_{2}\right\| \sqrt{3}}{2}&=0 \\ (E 2) \frac{\left\|\vec{T}_{1}\right\| \sqrt{3}}{2}+\frac{\left\|\vec{T}_{2}\right\|}{2}-50&=0 \end{array}\right.\nonumber$$ Від$(E 1)$, отримуємо$\left\|\vec{T}_{1}\right\|=\left\|\vec{T}_{2}\right\| \sqrt{3}$. Підставляючи те, що в$(E 2)$ дає,$\frac{\left(\left\|\overrightarrow{T_{2}}\right\| \sqrt{3}\right) \sqrt{3}}{2}+\frac{\left\|\vec{T}_{2}\right\|}{2}-50=0$ яка дає врожайність$2\left\|\vec{T}_{2}\right\|-50=0$. Значить,$\left\|\vec{T}_{2}\right\|=25$ фунти і$\left\|\vec{T}_{1}\right\|=\left\|\vec{T}_{2}\right\| \sqrt{3}=25 \sqrt{3}$ фунти.

11.8.1 Вправи

У вправах 1 - 10 використовуйте задану пару векторів$\vec{v}$ і$\vec{w}$ знайдіть наступні величини. Вкажіть, чи є результат вектором або скаляром.

• $\vec{v}+\vec{w}$
• $\vec{w}-2 \vec{v}$
• $\|\vec{v}+\vec{w}\|$
• $\|\vec{v}\|+\|\vec{w}\|$
• $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}$
• $\|\vec{w}\| \hat{v}$

Нарешті, переконайтеся, що вектори задовольняють закону паралелограма

$\|\vec{v}\|^{2}+\|\vec{w}\|^{2}=\frac{1}{2}\left[\|\vec{v}+\vec{w}\|^{2}+\|\vec{v}-\vec{w}\|^{2}\right]$

1. $\vec{v}=\langle 12,-5\rangle, \vec{w}=\langle 3,4\rangle$
2. $\vec{v}=\langle-7,24\rangle, \vec{w}=\langle-5,-12\rangle$
3. $\vec{v}=\langle 2,-1\rangle, \vec{w}=\langle-2,4\rangle$
4. $\vec{v}=\langle 10,4\rangle, \vec{w}=\langle-2,5\rangle$
5. $\vec{v}=\langle-\sqrt{3}, 1\rangle, \vec{w}=\langle 2 \sqrt{3}, 2\rangle$
6. $\vec{v}=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle, \vec{w}=\left\langle-\frac{4}{5}, \frac{3}{5}\right\rangle$
7. $\vec{v}=\left\langle\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle, \vec{w}=\left\langle-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right\rangle$
8. $\vec{v}=\left\langle\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle, \vec{w}=\langle-1,-\sqrt{3}\rangle$
9. $\vec{v}=3 \hat{\imath}+4 \hat{\jmath}, \vec{w}=-2 \hat{\jmath}$
10. $\vec{v}=\frac{1}{2}(\hat{\imath}+\hat{\jmath}), \vec{w}=\frac{1}{2}(\hat{\imath}-\hat{\jmath})$

У вправах 11 - 25 знайдіть складову форму вектора,$\vec{v}$ використовуючи дані про його величину і напрямок. Дайте точні значення.

11. $\|\vec{v}\|=6$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті I і робить$60^{\circ}$ кут з позитивною$x$ -віссю
12. $\|\vec{v}\|=3$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті I і робить$45^{\circ}$ кут з позитивною$x$ -віссю
13. $\|\vec{v}\|=\frac{2}{3}$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті I і робить$60^{\circ}$ кут з позитивною$y$ -віссю
14. $\|\vec{v}\|=12$; при накресленні в стандартному положенні$\vec{v}$ лежить вздовж позитивної$y$ -осі
15. $\|\vec{v}\|=4$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті II і робить$30^{\circ}$ кут з негативною$x$ віссю
16. $\|\vec{v}\|=2 \sqrt{3}$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті II і робить$30^{\circ}$ кут з позитивною$y$ -віссю
17. $\|\vec{v}\|=\frac{7}{2}$; при накресленні в стандартному положенні$\vec{v}$ лежить уздовж негативної$x$ осі
18. $\|\vec{v}\|=5 \sqrt{6}$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті III і робить$45^{\circ}$ кут з негативною$x$ віссю
19. $\|\vec{v}\|=6.25$; при накресленні в стандартному положенні$\vec{v}$ лежить уздовж негативної$y$ осі
20. $\|\vec{v}\|=4 \sqrt{3}$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті IV і робить$30^{\circ}$ кут з позитивною$x$ -віссю
21. $\|\vec{v}\|=5 \sqrt{2}$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті IV і робить$45^{\circ}$ кут з негативною$y$ віссю
22. $\|\vec{v}\|=2 \sqrt{5}$; при накресленні в стандартному положенні$\vec{v}$ лежить в квадранті I і робить кут вимірювання арктана (2) з позитивною$x$ -віссю
23. $\|\vec{v}\|=\sqrt{10}$; при накресленні в стандартному положенні$\vec{v}$ лежить в квадранті II і робить кут вимірювання арктана (3) з негативною$x$ віссю
24. $\|\vec{v}\|=5$; при накресленні в стандартному положенні$\vec{v}$ лежить в квадранті III і робить кут вимірювання$\arctan \left(\frac{4}{3}\right)$ з негативною$x$ віссю
25. $\|\vec{v}\|=26$; при малюванні в стандартному положенні$\vec{v}$ лежить в квадранті IV і робить кут вимірювання$\arctan \left(\frac{5}{12}\right)$ з позитивною$x$ віссю

У вправах 26 - 31 наближають складову форму вектора,$\vec{v}$ використовуючи інформацію, наведену про його величину і напрямок. Округліть ваші наближення до двох знаків після коми.

26. $\|\vec{v}\|=392$; при накресленні в стандартному положенні$\vec{v}$ робить$117^{\circ}$ кут з позитивною$x$ -віссю
27. $\|\vec{v}\|=63.92$; при накресленні в стандартному положенні$\vec{v}$ робить$78.3^{\circ}$ кут з позитивною$x$ -віссю
28. $\|\vec{v}\|=5280$; при накресленні в стандартному положенні$\vec{v}$ робить$12^{\circ}$ кут з позитивною$x$ -віссю
29. $\|\vec{v}\|=450$; при накресленні в стандартному положенні$\vec{v}$ робить$210.75^{\circ}$ кут з позитивною$x$ -віссю
30. $\|\vec{v}\|=168.7$; при накресленні в стандартному положенні$\vec{v}$ робить$252^{\circ}$ кут з позитивною$x$ -віссю
31. $\|\vec{v}\|=26$; при накресленні в стандартному положенні$\vec{v}$ маскує$304.5^{\circ}$ кут з позитивною$x$ -віссю

У Вправах 32 - 52 для даного вектора$\vec{v}$ знайдіть величину$\|\vec{v}\|$ і кут$\theta$ з$0 \leq \theta<360^{\circ}$ таким чином$\vec{v}=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle$ (Див. Визначення 11.8.) Округлені наближення до двох знаків після коми.

32. $\vec{v}=\langle 1, \sqrt{3}\rangle$
33. $\vec{v}=\langle 5,5\rangle$
34. $\vec{v}=\langle-2 \sqrt{3}, 2\rangle$
35. $\vec{v}=\langle-\sqrt{2}, \sqrt{2}\rangle$
36. $\vec{v}=\left\langle-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle$
37. $\vec{v}=\left\langle-\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle$
38. $\vec{v}=\langle 6,0\rangle$
39. $\vec{v}=\langle-2.5,0\rangle$
40. $\vec{v}=\langle 0, \sqrt{7}\rangle$
41. $\vec{v}=-10 \hat{\jmath}$
42. $\vec{v}=\langle 3,4\rangle$
43. $\vec{v}=\langle 12,5\rangle$
44. $\vec{v}=\langle-4,3\rangle$
45. $\vec{v}=\langle-7,24\rangle$
46. $\vec{v}=\langle-2,-1\rangle$
47. $\vec{v}=\langle-2,-6\rangle$
48. $\vec{v}=\hat{\imath}+\hat{\jmath}$
49. $\vec{v}=\hat{\imath}-4 \hat{\jmath}$
50. $\vec{v}=\langle 123.4,-77.05\rangle$
51. $\vec{v}=\langle 965.15,831.6\rangle$
52. $\vec{v}=\langle-114.1,42.3\rangle$
53. Невеликий човен залишає док в таборі Dunuthin і прямує через річку Нессі зі швидкістю 17 миль на годину (тобто по відношенню до води) при підшипнику S68◦ W Річка тече через схід зі швидкістю 8 миль на годину. Яка справжня швидкість і рух човна? Округлите швидкість до найближчої милі на годину і висловіть заголовок у вигляді підшипника, округленого до найближчої десятої частки градуса.
54. HMS Sasquatch залишає порт з підшипником,$\mathrm{S} 20^{\circ} \mathrm{E}$ підтримуючи швидкість 42 миль на годину (тобто по відношенню до води). Якщо океанська течія становить 5 миль на годину з підшипником$\mathrm{N} 60^{\circ} \mathrm{E}$, знайдіть справжню швидкість і підшипник HMS Sasquatch. Округлите швидкість до найближчої милі на годину і висловіть заголовок у вигляді підшипника, округленого до найближчої десятої частки градуса.
55. Якщо капітан HMS Sasquatch у навчанні 54 бажає досягти бухти Чупакабра, острів 100 миль$\mathrm{S} 20^{\circ} \mathrm{E}$ від порту, за три години, яку швидкість і курс вона повинна встановити, щоб врахувати океанічну течію? Округлите швидкість до найближчої милі на годину і висловіть заголовок у вигляді підшипника, округленого до найближчої десятої частки градуса.

    ПІДКАЗКА: Якщо$\vec{v}$ позначає швидкість HMS Sasquatch і$\vec{w}$ позначає швидкість течії, що$\vec{v}+\vec{w}$ потрібно, щоб дістатися до бухти Чупакабра за три години?

56. У спокійному повітрі літак, що летить з міжнародного аеропорту Pedimaxus, може дістатися до Скелі безумства за дві години, слідуючи підшипнику$\mathrm{N} 8.2^{\circ} \mathrm{E}$ на 96 миль на годину. (Відстань між аеропортом і скелями - 192 милі.) Якщо вітер дме з південного сходу зі швидкістю 25 миль на годину, яку швидкість і підшипник повинен взяти пілот, щоб вона здійснила поїздку за дві години по початковому курсу? Округляйте швидкість до найближчої сотої частки милі на годину і свій кут до найближчої десятої частки градуса.
57. Снігова людина СС залишає затоку Йеті на курсі зі$\mathrm{N} 37^{\circ} \mathrm{W}$ швидкістю 50 миль на годину. Проїхавши півгодини, капітан визначає, що він знаходиться в 30 милі від затоки і його підшипник назад до бухти$\mathrm{S} 40^{\circ} \mathrm{E}$. Яка швидкість і підшипник океанічної течії? Округлите швидкість до найближчої милі на годину і висловіть заголовок у вигляді підшипника, округленого до найближчої десятої частки градуса.
58. Статуя Саскватча 600 фунтів підвішена двома кабелями від стелі гімназії. Якщо кожен кабель робить$60^{\circ}$ кут зі стелею, знайдіть натяг на кожному кабелі. Округліть відповідь до найближчого фунта.
59. Два кабелі призначені для підтримки об'єкта, що звисає зі стелі. Якщо кабелі мають зробити$42^{\circ}$ кут зі стелею, і кожен кабель розрахований на максимальну напругу 100 фунтів, який найважчий предмет, який можна підтримувати? Округліть відповідь до найближчого фунта.
60. Металева зірка 300 фунтів висить на двох кабелів, які прикріплені до стелі. Лівий трос робить$72^{\circ}$ кут зі стелею, тоді як правий кабель робить$18^{\circ}$ кут зі стелею. Яке натяг на кожному з тросів? Округляйте відповіді до трьох знаків після коми.
61. Двоє п'яних студентів коледжу наповнили порожню пивну бочку з камінням і прив'язали до нього мотузки, щоб перетягнути його по вулиці посеред ночі. Сильніший з двох студентів тягне з силою 100 фунтів на заголовок,$\mathrm{N} 77^{\circ} \mathrm{E}$ а інший тягне в заголовок$\mathrm{S} 68^{\circ} \mathrm{E}$. Яку силу слабший школяр повинен докласти до своєї мотузки, щоб бочонок скель очолив через схід? Яка результуюча сила прикладається до бочки? Округліть відповідь до найближчого фунта.
62. Підбадьорений успіхом їх пізньої ночі бочонок тягнути у вправі 61 вище, наші безстрашні молоді вчені вирішили віддати належне сцені гонки колісниць з фільму «Бен-Гур», прив'язавши три мотузки до дивана, завантажуючи диван з усіма, крім одного зі своїх друзів, і потягнувши його через захід вниз по вулиці. Перша мотузка вказує$\mathrm{N} 80^{\circ} \mathrm{W}$, друга вказує на захід і третя точка$\mathrm{S} 80^{\circ} \mathrm{W}$. Сила, прикладена до першої мотузки, становить 100 фунтів, сила, прикладена до другої мотузки, становить 40 фунтів, а сила, прикладена (не їде друг) до третьої мотузки - 160 фунтів. Їм потрібна результуюча сила, щоб бути не менше 300 фунтів, інакше диван не рухатиметься. Чи рухається він? Якщо так, то чи рухається він через захід?
63. $\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$Дозволяти будь ненульовий вектор. Показати, що$\frac{1}{\|\vec{v}\|} \vec{v}$ має довжину 1.
64. Ми говоримо, що два ненульових вектора$\vec{v}$ і$\vec{w}$ паралельні, якщо вони мають однакові або протилежні напрямки. Тобто,$\vec{v} \neq \overrightarrow{0}$ і$\vec{w} \neq \overrightarrow{0}$ паралельні, якщо$\hat{v}=\hat{w}$ або$\hat{v}=-\hat{w}$. Показати, що це означає$\vec{v}=k \vec{w}$ для деяких ненульових скалярних$k$ і що$k > 0$ якщо вектори мають однаковий напрямок і$k < 0$ якщо вони вказують в протилежних напрямках.
65. Мета цієї вправи - використовувати вектори для опису невертикальних ліній на площині. З цією метою розглянемо лінію$y=2 x-4$. Нехай$\vec{v}_{0}=\langle 0,-4\rangle$ і нехай$\vec{s}=\langle 1,2\rangle$. $t$Дозволяти бути будь-яке дійсне число. Показати, що вектор, визначений$\vec{v}=\vec{v}_{0}+t \vec{s}$, коли він намальований у стандартному положенні, має свою кінцеву точку на лінії$y = 2x − 4$. (Підказка: Покажіть, що$\vec{v}_{0}+t \vec{s}=\langle t, 2 t-4\rangle$ для будь-якого реального числа$t$.) Тепер розглянемо невертикальну лінію$y = mx+b$. Повторіть попередній аналіз з$\vec{v}_{0}=\langle 0, b\rangle$ і нехай$\vec{s}=\langle 1, m\rangle$. Таким чином, будь-яку невертикальну лінію можна розглядати як сукупність кінцевих точок векторної суми$\langle 0, b\rangle$ (вектора положення$y$ -перехоплення) та скалярного вектора, кратного вектору нахилу$\vec{s}=\langle 1, m\rangle$.
66. Довести асоціативні та ідентичні властивості векторного додавання в теоремі 11.18.
67. Довести властивості скалярного множення в теоремі 11.19.

11.8.2 Відповіді

1. • $\vec{v}+\vec{w}=\langle 15,-1\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-21,14\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=\sqrt{226}, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=18, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-21,77\rangle, \text { vector }$
   • $\|w\| \hat{v}=\left\langle\frac{60}{13},-\frac{25}{13}\right\rangle, \text { vector }$
2. • $\vec{v}+\vec{w}=\langle-12,12\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle 9,-60\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=12 \sqrt{2}, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=38, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-34,-612\rangle, \text { vector }$
   • $\|w\| \hat{v}=\left\langle-\frac{91}{25}, \frac{312}{25}\right\rangle, \text { vector }$
3. • $\vec{v}+\vec{w}=\langle 0,3\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-6,6\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=3, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=3 \sqrt{5}, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-6 \sqrt{5}, 6 \sqrt{5}\rangle, \text { vector }$
   • $\|w\| \hat{v}=\langle 4,-2\rangle, \text { vector }$
4. • $\vec{v}+\vec{w}=\langle 8,9\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-22,-3\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=\sqrt{145}, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=3 \sqrt{29}, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-14 \sqrt{29}, 6 \sqrt{29}\rangle, \text { vector }$
   • $\|w\| \hat{v}=\langle 5,2\rangle, \text { vector }$
5. • $\vec{v}+\vec{w}=\langle\sqrt{3}, 3\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle 4 \sqrt{3}, 0\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=2 \sqrt{3}, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=6, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle 8 \sqrt{3}, 0\rangle, \text { vector }$
   • $\|w\| \hat{v}=\langle-2 \sqrt{3}, 2\rangle, \text { vector }$
6. • $\vec{v}+\vec{w}=\left\langle-\frac{1}{5}, \frac{7}{5}\right\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-2,-1\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=\sqrt{2} \text {, scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=2, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\left\langle-\frac{7}{5},-\frac{1}{5}\right\rangle, \text { vector }$
   • $\|w\| \hat{v}=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle, \text { vector }$
7. • $\vec{v}+\vec{w}=\langle 0,0\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\left\langle-\frac{3 \sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=0, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=2, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-\sqrt{2}, \sqrt{2}\rangle, \text { vector }$
   • $\|w\| \hat{v}=\left\langle\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle, \text { vector }$
8. • $\vec{v}+\vec{w}=\left\langle-\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-2,-2 \sqrt{3}\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=1, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=3, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-2,-2 \sqrt{3}\rangle, \text { vector }$
   • $\|w\| \hat{v}=\langle 1, \sqrt{3}\rangle, \text { vector }$
9. • $\vec{v}+\vec{w}=\langle 3,2\rangle, \text { vector }$
   • $\vec{w}-2 \vec{v}=\langle-6,-10\rangle, \text { vector }$
   • $\|\vec{v}+\vec{w}\|=\sqrt{13}, \text { scalar }$
   • $\|\vec{v}\|+\|\vec{w}\|=7, \text { scalar }$
   • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-6,-18\rangle, \text { vector }$
   • $\|w\| \hat{v}=\left\langle\frac{6}{5}, \frac{8}{5}\right\rangle, \text { vector }$
10. • $\vec{v}+\vec{w}=\langle 1,0\rangle, \text { vector }$
    • $\vec{w}-2 \vec{v}=\left\langle-\frac{1}{2},-\frac{3}{2}\right\rangle, \text { vector }$
    • $\|\vec{v}+\vec{w}\|=1, \text { scalar }$
    • $\|\vec{v}\|+\|\vec{w}\|=\sqrt{2}, \text { scalar }$
    • $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\left\langle 0,-\frac{\sqrt{2}}{2}\right\rangle, \text { vector }$
    • $\|w\| \hat{v}=\left\langle\frac{1}{2}, \frac{1}{2}\right\rangle, \text { vector }$
11. $\vec{v}=\langle 3,3 \sqrt{3}\rangle$
12. $\vec{v}=\left\langle\frac{3 \sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right\rangle$
13. $\vec{v}=\left\langle\frac{\sqrt{3}}{3}, \frac{1}{3}\right\rangle$
14. $\vec{v}=\langle 0,12\rangle$
15. $\vec{v}=\langle-2 \sqrt{3}, 2\rangle$
16. $\vec{v}=\langle-\sqrt{3}, 3\rangle$
17. $\vec{v}=\left\langle-\frac{7}{2}, 0\right\rangle$
18. $\vec{v}=\langle-5 \sqrt{3},-5 \sqrt{3}\rangle$
19. $\vec{v}=\langle 0,-6.25\rangle$
20. $\vec{v}=\langle 6,-2 \sqrt{3}\rangle$
21. $\vec{v}=\langle 5,-5\rangle$
22. $\vec{v}=\langle 2,4\rangle$
23. $\vec{v}=\langle-1,3\rangle$
24. $\vec{v}=\langle-3,-4\rangle$
25. $\vec{v}=\langle 24,-10\rangle$
26. $\vec{v} \approx\langle-177.96,349.27\rangle$
27. $\vec{v} \approx\langle 12.96,62.59\rangle$
28. $\vec{v} \approx\langle 5164.62,1097.77\rangle$
29. $\vec{v} \approx\langle-386.73,-230.08\rangle$
30. $\vec{v} \approx\langle-52.13,-160.44\rangle$
31. $\vec{v} \approx\langle 14.73,-21.43\rangle$
32. $\|\vec{v}\|=2, \theta=60^{\circ}$
33. $\|\vec{v}\|=5 \sqrt{2}, \theta=45^{\circ}$
34. $\|\vec{v}\|=4, \theta=150^{\circ}$
35. $\|\vec{v}\|=2, \theta=135^{\circ}$
36. $\|\vec{v}\|=1, \theta=225^{\circ}$
37. $\|\vec{v}\|=1, \theta=240^{\circ}$
38. $\|\vec{v}\|=6, \theta=0^{\circ}$
39. $\|\vec{v}\|=2.5, \theta=180^{\circ}$
40. $\|\vec{v}\|=\sqrt{7}, \theta=90^{\circ}$
41. $\|\vec{v}\|=10, \theta=270^{\circ}$
42. $\|\vec{v}\|=5, \theta \approx 53.13^{\circ}$
43. $\|\vec{v}\|=13, \theta \approx 22.62^{\circ}$
44. $\|\vec{v}\|=5, \theta \approx 143.13^{\circ}$
45. $\|\vec{v}\|=25, \theta \approx 106.26^{\circ}$
46. $\|\vec{v}\|=\sqrt{5}, \theta \approx 206.57^{\circ}$
47. $\|\vec{v}\|=2 \sqrt{10}, \theta \approx 251.57^{\circ}$
48. $\|\vec{v}\|=\sqrt{2}, \theta \approx 45^{\circ}$
49. $\|\vec{v}\|=\sqrt{17}, \theta \approx 284.04^{\circ}$
50. $\|\vec{v}\| \approx 145.48, \theta \approx 328.02^{\circ}$
51. $\|\vec{v}\| \approx 1274.00, \theta \approx 40.75^{\circ}$
52. $\|\vec{v}\| \approx 121.69, \theta \approx 159.66^{\circ}$
53. Справжня швидкість човна становить близько 10 миль на годину в рубриці$\mathrm{S} 50.6^{\circ} \mathrm{W}$.
54. Справжня швидкість HMS Sasquatch становить близько 41 милі на годину в русі$\mathrm{S} 26.8^{\circ} \mathrm{E}$.
55. Вона повинна підтримувати швидкість близько 35 миль на годину при русі$\mathrm{S} 11.8^{\circ} \mathrm{E}$.
56. Вона повинна літати зі швидкістю 83.46 миль на годину із заголовком$\mathrm{N} 22.1^{\circ} \mathrm{E}$
57. Струм рухається зі швидкістю близько 10 миль на годину підшипника$\mathrm{N} 54.6^{\circ} \mathrm{W}$.
58. Напруга на кожному з кабелів становить близько 346 фунтів.
59. Максимальна вага, яку можуть утримувати кабелі в цій конфігурації, становить близько 133 фунтів.
60. Натяг лівого троса становить 285,317 фунтів. а на правій руці - 92,705 фунтів.
61. Більш слабкий школяр повинен тягнути близько 60 фунтів. Чиста сила на бочку становить близько 153 фунтів.
62. Отримана сила становить лише близько 296 фунтів, тому диван не зрушується з місця. Навіть якби він рухався, сильніша сила на третій мотузці змусила б диван трохи дрейфувати на південь, коли він їхав по вулиці.

---

Довідка

¹ Слово «вектор» походить від латинського vehere, що означає «транспортувати» або «нести».

² Інші автори підручників використовують жирні вектори, такі як$\boldsymbol{v}$. Ми виявляємо, що писати жирним шрифтом на дошці в кращому випадку незручно, тому ми вибрали позначення «стрілка».

³ Якщо ця ідея «над» і «вгору» здається знайомою, вона повинна. Нахил відрізка лінії, що містить$\vec{v}$ дорівнює$\frac{4}{3}$.

⁴ При необхідності перегляньте сторінку 905 і розділ 11.3.

⁵ Тобто швидкість літака щодо повітря навколо нього. Якби не було вітру, швидкість польоту літака була б такою ж, як і його швидкість, яка спостерігається з землі. Як на це впливає вітер? Продовжуйте читати!

⁶ Див. розділ 10.1.1, наприклад.

⁷ Або, оскільки наш заданий кут$100^{\circ}$, тупий, ми могли б використовувати Закон Синеса без будь-якої неоднозначності тут.

⁸ Додавання векторів «компонентно-мудрим» має здатися звично знайомим. Порівняйте це з тим, як було визначено додавання матриць у розділі 8.3. Насправді, в більш просунутих курсах, таких як Лінійна алгебра, вектори визначаються як$1 \times n$ або$n \times 1$ матриці, залежно від ситуації.

⁹ Зацікавленому читачеві пропонується порівняти теорему 11.18 та подальшу дискусію з теоремою 8.3 у розділі 8.3 та обговорення там.

¹⁰ Якщо це все виглядає звично, це повинно. Зацікавленому читачеві пропонується порівняти визначення 11.8 з визначенням 11.2 у розділі 11.7.

¹¹ Звичайно, щоб перейти від$\vec{v}=\|\vec{v}\| \hat{v}$ до$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$, ми по суті «ділимо обидві сторони» рівняння скаляром$\|\vec{v}\|$. Однак автори заохочують читача ретельно опрацювати деталі, щоб отримати оцінку властивостей у грі.

¹² Через корисність векторів у «реальних» додатках ми зазвичай використовуємо градусну міру для кута, коли вказуємо напрямок вектора. Однак, оскільки Карл не хоче, щоб ви забули про радіани, він переконався, що є приклади та вправи, які їх використовують.

¹³ Зберігання речей «калькулятор» дружнім, на один раз!

¹⁴ Так, наближення калькулятора - це найшвидший спосіб побачити це, але ви також можете використовувати старі добрі нерівності та те, що$45^{\circ} \leq 50^{\circ} \leq 60^{\circ}$.

¹⁵ Один доказ використовує властивості скалярного множення і величини. Якщо$\vec{v} \neq \overrightarrow{0}$, врахуйте$\|\hat{v}\|=\left\|\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}\right\|$. Використовуйте той факт, що$\|\vec{v}\| \geq 0$ є скалярним і розгляньте факторинг.

¹⁶.$\|\vec{v}\|>1$. якщо.

¹⁷ Ми побачимо узагальнення теореми 11.21 у розділі 11.9. Слідкуйте за оновленнями!

¹⁸ Див. також розділ 11.1.1.

¹⁹ Це критерії «статичного рівноправності».