1.1: Вступ

Розв'язування звичайних диференціальних рів

Розв'язування звичайних диференціальних рівнянь (ОДУ) є основним напрямком чисельних обчислень. Почнемо з розгляду ОДУ першого порядку форми

\[\tag{eq:1.1} y' = f(t, y)\]

Де\(y(t)\) знаходиться невідоме (тобто річ, яку ми хочемо знайти), і\(t\) є незалежною змінною. Маючи справу з такою ОДА, ми зазвичай думаємо\(t\) як про час, і\(y\) як щось, що залежить від часу, як популяція виду тварин або напруга вузла в електронній схемі. Рівняння [eq:1.1] говорить, що спосіб\(y\) зміни часу залежить від якоїсь функції\(f\). У цьому буклеті ми припускаємо, що функція\(f\) є гладкою і добре поводиться, і що вона легко обчислюється в комп'ютерній програмі.

Можна записати рішення до [eq:1.1], але для отримання унікального рішення потрібна додаткова інформація: Початкова умова. Тобто нам потрібно щось знати в один\(y(t)\) момент часу, щоб ми могли вибрати одне індивідуальне рішення з усіх можливих рішень, які задовольняють [eq:1.1]. Традиційно використовується значення для\(y(t)\) часу\(t=0\) як початкова умова, але інші варіанти також можливі (але незвичні).

Ось дуже простий приклад. Розглянемо ОДА\[\tag{eq:1.2} y' = a y\] Ви, ймовірно, зіткнулися з цією ОДА на початку своєї математичної кар'єри, і ви знаєте рішення напам'ять:\[\tag{eq:1.3} y(t) = C e^{a t}\] де\(C\) якась константа. Рішення [еква:1.3] очевидно задовольняє рівнянню [еква:1.2], але воно не є корисним на практиці як рішення рівняння. Чому? Причина в тому, що існує нескінченна кількість можливих рішень в залежності від\(C\) обраного значення. Тобто, [eq:1.3] визначає сімейство рішень, але в реальній, практичній проблемі ми хочемо лише одного з цих рішень. Наприклад, як би ви зробили сюжет [eq:1.3]? Відповідь полягає в тому, що ви не можете, поки не вибрали конкретне значення\(C\).

У практичній задачі, ви зазвичай знаєте значення вашої функції в початковій точці часу, майже завжди в\(t = 0\). Назвіть це значення\(y_0\). У цьому випадку конкретне рішення, яке задовольняє [eq:1.2], а також\(y(t=0) = y_0\) задовольняє є\[\tag{eq:1.4} y(t) = y_0 e^{a t}\] Справа в тому, що для чисельного вирішення ОДА потрібні дві частини інформації: 1. Сама ОДА, і 2. Початкова умова. Початкове значення вибирає один розв'язок з усього сімейства розв'язків, які задовольняють [екв:1.2]. Поняття показано в 1.1

Малюнок 1.1: ОДА\(y' = f(t,y)\) задовольняється сімейством кривих. Початкова умова\(y(0)\) необхідна для вибору одного з рішень для числового моделювання.

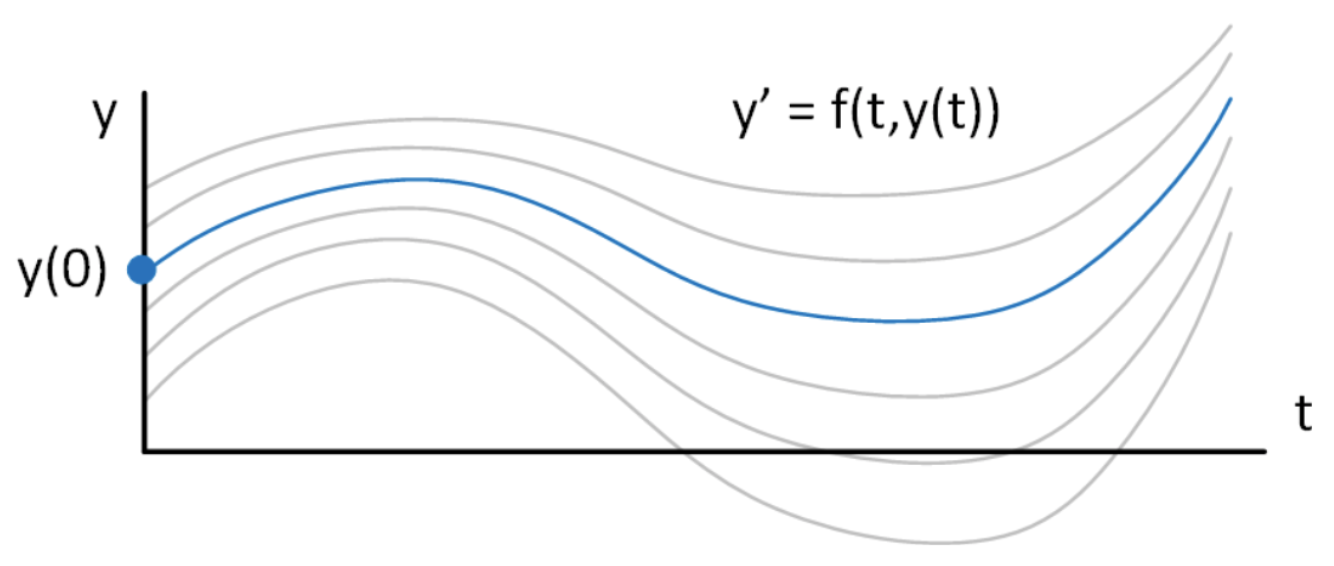
Така задача називається «задачею початкового значення» (IVP), щоб відрізнити її від інших типів диференціальних рівнянь (з якими ми зіткнемося пізніше в класі). «Проблема початкового значення» просто означає, що ми знаємо початкове (початкове) значення і хочемо знайти її поведінку\(y\), коли ми рухаємося вперед у часі. Після того, як рівняння [eq:1.1] та початкова умова для\(y\) вказані, ми маємо всю інформацію, необхідну для чисельного пошуку\(y(t)\) унікального рішення.

Методи пошуку числових рішень IVP знаходяться в центрі уваги цієї брошури. Що стосується номенклатури, то ми взагалі говоримо «вирішити ОДА», або «вирішити IVP». Це означає, що ми обчислюємо функцію,\(y(t)\) починаючи від часу\(t=0\) до певного моменту в майбутньому\(t_{end}\). Ще один спосіб сказати те саме - ми «інтегруємо ODE» або «інтегруємо IVP». Говорячи про ОДУ, «інтегрувати» означає те ж саме, що і «вирішити».

Вибіркові функції

У математиці ми знайомимося з поняттям функції. Розглянемо найпростіший випадок функції,\(y(t)\) яка приймає дійсний скаляр\(t\) і повертає дійсне скалярне значення\(y(t)\). Це часто пишеться формально як\(y:\mathbb{R}\rightarrow \mathbb{R}\). Це означає, що візьміть будь-яке довільне дійсне число\(t\)\(y\), підключіть його до, і вийде нове дійсне число\(y(t)\). Важливою ідеєю, щоб отримати від цього, є те, що функція схожа на машину, в яку можна ввести будь-який\(t\) і очікувати, щоб отримати вихід. Тобто функція визначається на кожному дійсному числі\(t\).

На жаль, при роботі над реальними даними за допомогою комп'ютера ця приємна абстракція не завжди тримається. Швидше за все, для нас дуже часто є лише певні, дискретні точки,\(t_n\) де визначена функція. Цифровий звук - це простий приклад: звуки, які ми чуємо вухом, пов'язані з хвилями звукового тиску, що рухають наші барабанні перетинки. Звуковий тиск має значення для кожного моменту часу. Але при обробці аудіо за допомогою комп'ютера звуковий тиск дискретизується в звичайний, дискретний час і перетворюється на числа, що представляють звуковий тиск у кожному вибірковому часі. Цей процес часто називають «дискретизацією», що означає, що безперервно визначене\(y(t)\) замінюється набором дискретних зразків\(y_n\). Це зображено в 1.2, який показує взаємозв'язок функції безперервного часу та її дискретно-часової (дискретизованої) заміни.

Малюнок 1.2: Вибіркова функція. Безперервна версія функції є\(y(t)\). Відбір проб замінює\(y(t)\) зразками, взятими в дискретний час,\(t_n\). Зразки\(y_n\) можуть оброблятися комп'ютером у вигляді вектора або списку значень. У показаному тут випадку функція вибірка здійснюється через рівномірні інтервали, розділені між собою\(h\). Рівномірні зразки є найбільш частим випадком - наприклад, цифровий звук зазвичай вибірки вхідного звукового сигналу з\(h\) періодом близько 22.7usec (частота дискретизації 44.1 кГц).

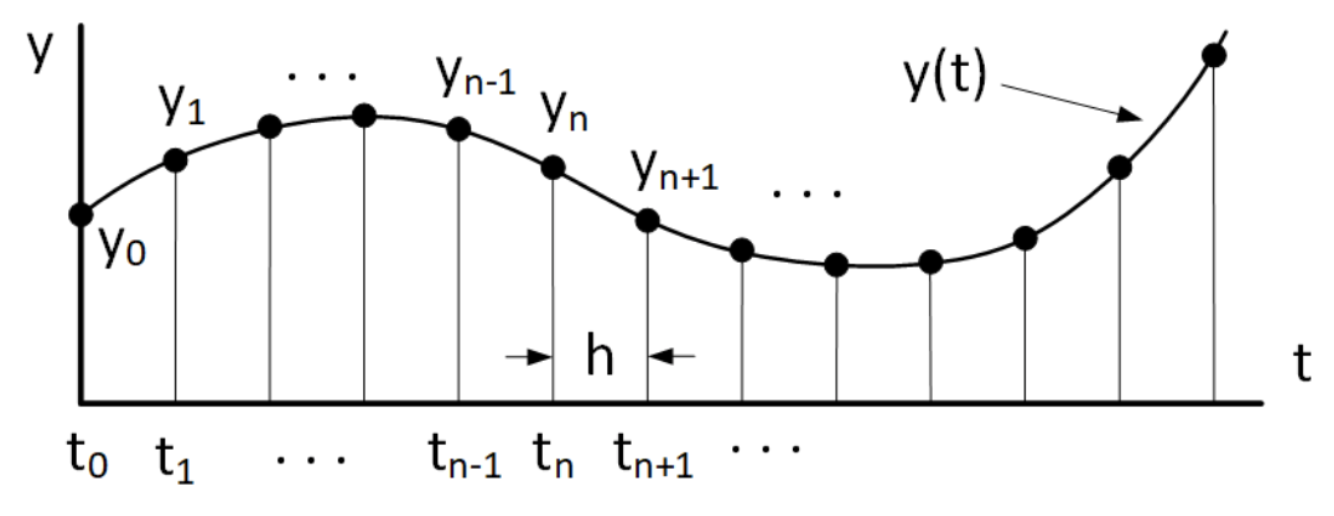
Виходить, що розв'язувачі ODE ми вивчимо всю роботу з вибірковими функціями. Тобто розв'язувачі обчислюють рішення\(y(t)\) при послідовності дискретних значень часу,\(t_n\) аналогічних ситуації, наведеної в 1.2. Виходом розв'язувача буде вектор дискретних значень,\(y_n\) що представляють зразки фактичної, що лежить в основі неперервної функції\(y(t)\).

Ось підказка щодо реалізації під час написання програм, що обробляють вибіркові функції: Сама функція sampled зазвичай представлена вектором,\(y_n\). Саме цей об'єкт буде використовувати ваш алгоритм під час своєї роботи. На вершині\(y_n\) я рекомендую також носити навколо вектора, що представляє час вибірки\(t_n\), у вашій програмі. Наявність доступного часу вибірки може допомогти зменшити плутанину, наприклад, коли ви хочете побудувати сюжет\(y_n\) проти часу. Для векторів помірного розміру додаткова пам'ять, необхідна для зберігання,\(t_n\) - це невелика ціна, яку потрібно заплатити, щоб зберегти плутанину на мінімумі під час написання коду.

Диференціація на комп'ютері

Далі перед тим, як зануритися в рішення [eq:1.1] нам потрібно переглянути, як відбувається диференціація на комп'ютері. Для початку згадайте визначення похідної,\(y(t)\) яку ви, ймовірно, дізналися в середній школі:\[\tag{eq:1.5} \frac{d y}{d t} = \lim_{{\Delta t}\to 0} \frac{y(t + \Delta t) - y(t)}{\Delta t}\] Виконуючи числові обчислення, ми не можемо представити граничний перехід\(\lim_{{\Delta t}\to 0}\) - наші дані зазвичай дискретні (наприклад, вибіркова функція). Що ще важливіше, числа з плаваючою комою не плавно переходять до нуля - на комп'ютері немає «нескінченно маленького, але ненульового» числа. Натомість ми використовуємо визначення [eq:1.5], щоб сформувати наближення до похідної, як\[\tag{eq:1.6} \frac{d y}{d t} \approx \frac{y(t + h) - y(t)}{h}\] де\(h\) невелике число. Це називається «прямою різницею» наближення похідної.

Перші похідні з серії Тейлора

Легко записати наближення [eq:1.6], запам'ятавши визначення похідної середньої школи. Однак ми отримуємо деяку оцінку точності наближення похідних, отримуючи їх за допомогою розширень рядів Тейлора. Припустимо, ми знаємо значення функції\(y\) в той час\(t\) і хочемо дізнатися її значення пізніше\(t+h\). Як знайти\(y(t+h)\)? Розширення серії Тейлора говорить, що ми можемо знайти значення пізніше\[\tag{eq:1.7} y(t+h) = y(t) + h \frac{d y}{d t} \biggr\rvert_{t} + \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} + \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] за допомогою Позначення\(O(h^4)\) означає, що в сумі є умови потужності\(h^4\) і вище, але ми розглянемо їх деталі, які ми можемо ігнорувати.

Ми можемо переставити [eq:1.7] поставити першу похідну на LHS, даючи\[\nonumber \frac{d y}{d t} \biggr\rvert_{t} = \frac{y(t+h) - y(t)}{h} - \frac{h}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} - \frac{h^2}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} - O(h^4)\] Тепер ми робимо припущення, що\(h\) дуже мало, тому ми можемо викинути умови порядку\(h\) і вище з цього виразу. З цим припущенням ми отримуємо,\[\nonumber y(t+h) \approx y(t) + h \frac{d y}{d t} \biggr\rvert_{t}\] які можна переставити, щоб дати,\[\tag{eq:1.8} \frac{d y}{d t} \approx \frac{y(t + h) - y(t)}{h}\] тобто той самий прямий вираз різниці, що і в [eq:1.6] раніше. Однак зауважте, що для отримання цього наближення ми викинули всі умови порядку\(h\) і вище. Це означає, що коли ми використовуємо це наближення, ми отримуємо помилку! Ця помилка буде на замовлення\(h\). У межі помилка\(h \rightarrow 0\) зникає, але оскільки комп'ютери можуть використовувати лише кінцевий\(h\), завжди буде помилка в наших обчисленнях, і помилка пропорційна\(h\). Ми виражаємо цю концепцію, кажучи шкали помилок як\(O(h)\).

Використовуючи розширення серії Тейлора, ми можемо виявити інші результати. Подумайте про те, щоб сидіти в точці часу\(t\) і запитати значення\(y\) часу\(t - h\) в минулому. У цьому випадку ми можемо написати вираз для минулого значення\(y\) як\[\tag{eq:1.9} y(t-h) = y(t) - h \frac{d y}{d t} \biggr\rvert_{t} + \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} - \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] Зверніть увагу на негативні знаки на термах непарного порядку. Подібно до прямої різниці виразу вище, легко переставити цей вираз, а потім викинути члени від\(O(h)\) і вище, щоб отримати інше наближення для похідної,\[\tag{eq:1.10} \frac{d y}{d t} \approx \frac{y(t) - y(t-h)}{h}\] Це називається «зворотною різницею» наближення до похідної. Оскільки ми викинули терміни\(O(h)\) і вище, цей вираз для похідної також несе штраф за помилку\(O(h)\).

Тепер розглянемо формування різниці між серіями Тейлора [eq:1.7] і [eq:1.9]. Коли ми віднімаємо одне від іншого, ми отримуємо\[\tag{eq:TaylorsExpansionDifference} \nonumber y(t+h) - y(t-h) = 2 h \frac{d y}{d t} \biggr\rvert_{t} + 2 \frac{h^3}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^5)\] Цей вираз може бути перебудований, щоб стати\[\nonumber \frac{d y}{d t} \biggr\rvert_{t} = \frac{y(t+h) - y(t-h)}{2 h} - \frac{h^2}{6} \frac{d^3 y}{d t^3} \biggr\rvert_{t} + O(h^4)\] Тепер, якщо ми викидаємо терміни\(O(h^2)\) і вище, ми отримаємо так звану «центральну різницю» наближення для похідної,\[\tag{eq:1.11} \frac{d y}{d t} \biggr\rvert_{t} \approx \frac{y(t+h) - y(t-h)}{2 h}\] Зверніть увагу, що для отримання цього виразу ми відкидаємо \(O(h^2)\)терміни. Це означає, що помилка, виникла при використанні цього виразу для похідної, є\(O(h^2)\). Оскільки ми зазвичай маємо\(h \ll 1\), центральна похибка різниці\(O(h^2)\) менша, ніж\(O(h)\) понесена при використанні формул різниці вперед або назад. Тобто, центральний різницевий вираз [eq:1.11] забезпечує більш точне наближення до похідної, ніж формули різниці вперед або назад, і має бути вашим кращим похідним наближенням, коли ви можете використовувати його.

У кожному з цих деривацій ми викидали терміни якогось порядку\(p\) (і вище). Відкидання умов замовлення\(p\) і вище означає, що у нас більше немає повної серії Тейлора. Ця операція називається «усічення», тобто ми обрізали (відрізали) інші терміни повного ряду Тейлора. Тому помилка, що виникає в результаті цієї операції, називається «помилка усічення».

Другі похідні з серії Тейлора

Ми також можемо отримати наближення для другої похідної від виразів [eq:1.7] і [eq:1.9]. На цей раз сформувати суму двох виразів, щоб отримати\[\nonumber \label{eq:TaylorsExpansionSum} y(t+h) + y(t-h) = 2 y(t) + 2 \frac{h^2}{2} \frac{d^2 y}{d t^2} \biggr\rvert_{t} +O(h^4)\] Це може бути перебудований, щоб отримати вираз для другої похідної,\[\nonumber \frac{d^2 y}{d t^2} \biggr\rvert_{t} = \frac{y(t+h) -2 y(t) + y(t-h)} {h^2} -O(h^2)\] Якщо ми скинемо\(O(h^2)\) термін, ми отримаємо наближення до другої похідної,\[\tag{eq:1.12} \frac{d^2 y}{d t^2} \biggr\rvert_{t} \approx \frac{y(t+h) -2 y(t) + y(t-h)} {h^2}\] І так як ми скинули\(O(h^2)\) термін до зробити це наближення, це означає, що використання [eq:1.12] спричинить помилку\(O(h^2)\) при використанні цього наближення.

Короткий зміст глави

Ось важливі моменти, зроблені в цьому розділі:

• Для вирішення ОДУ чисельно потрібні дві частини інформації: ОДА та початкова умова. Такі проблеми називаються «задачами початкової вартості», або IVP.
• Як математики, ми звикли до функцій,\(y(t)\) які приймають будь-яке безперервне значення\(t\) і випромінюють значення. Однак, маючи справу з комп'ютерами, ми повинні часто використовувати «вибіркові функції», в яких безперервний\(y(t)\) замінюється зразками,\(y_n\) взятими в регулярні, дискретні моменти часу,\(t_n\). Розв'язувачі ODE, представлені в цьому буклеті, потрапляють до цієї категорії — вони надають зразки рішення в дискретний час, подібні до знімків неперервної функції, яку вони намагаються наблизити.
• підсумовує чотири різні наближення для похідних, з якими ми стикалися досі. Є набагато більше похідних наближень вищого порядку, і з використанням більшої кількості термінів. Наближення більш високого порядку дають кращу точність ціною додаткової складності. Наближення більш високого порядку використовуються рідше, ніж чотири, показані тут.

Зазвичай використовуються кінцеві різницеві похідні.

Похідні	Назва методу	Вираз	Порядок помилок
\(\frac{d y}{d t}\)	Різниця вперед	\(\frac{y_{n+1}-y_n}{h}\)	\(h\)
\(\frac{d y}{d t}\)	Зворотна різниця	\(\frac{y_{n}-y_{n-1}}{h}\)	\(h\)
\(\frac{d y}{d t}\)	Центральна відмінність	\(\frac{y_{n+1}-y_{n-1}}{2 h}\)	\(h^2\)
\(\frac{d^2 y}{d t^2}\)	Друга похідна	\(\frac{y_{n+1}-2 y_{n}+y_{n-1}}{h^2}\)	\(h^2\)