1.1: Приклади

Last updated
Save as PDF

Page ID: 61880

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Приклад 1.1.1:

$u_y=0$, де$u=u(x,y)$. Всі функції$u=w(x)$ є рішеннями.

Приклад 1.1.2:

$u_x=u_y$, де$u=u(x,y)$. Зміна координат перетворює це рівняння в рівняння першого прикладу. Встановити$\xi=x+y,\ \eta=x-y$, потім
$$
u (x, y) =u\ ліворуч (\ frac {\ xi+\ eta} {2},\ frac {\ xi-\ eta} {2}\ праворуч) =:v (\ xi,\ eta).
$
Припустимо$u\in C^1$, тоді
$$
v_\ eta=\ frac {1} {2} (u_x-u_y).
$$
Якщо$u_x=u_y$, то$v_\eta=0$ і навпаки, таким чином,$v=w(\xi)$ є розв'язками для довільних$C^1$ -функцій$w(\xi)$. Отже, маємо великий клас розв'язків вихідного рівняння з частинними похідними:$u=w(x+y)$ з довільною$C^1$ -функцією$w$.

Приклад 1.1.3:

Необхідна і достатня умова така, що для заданих$C^1$ -функцій$M,\ N$
інтеграл $$
\ int_ {P_0} ^ {P_1}\ M (x, y) dx+n (x, y) dy
$$
не залежить від кривої, яка з'єднує точки$P_0$$P_1$ в простому зв'язку область$\Omega\subset\mathbb{R}^2$ полягає в тому, що рівняння з частинними похідними (умова інтегровності)
$$
M_Y=N_x
$$
в$\Omega$.

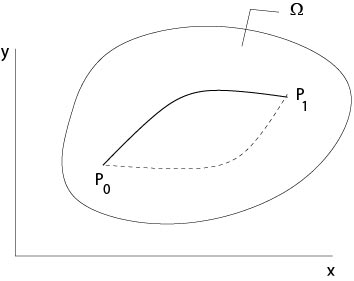
$незалежність шляху$

Малюнок 1.1.1: Незалежність шляху

Це одне рівняння для двох функцій. Великий клас розв'язків задається тим$M=\Phi_x,\ N=\Phi_y$, де$\Phi(x,y)$ - довільна$C^2$ -функція. З теореми Гаусса випливає, що це все$C^1$ -розв'язки вищевказаного диференціального рівняння.

Приклад 1.1.4: Метод інтегруючого множника для звичайного

диференціальний

рівняння

Розглянемо звичайне диференціальне рівняння
$$
M (x, y) Dx+n (x, y) dy=0
$$
для заданих$C^1$ -функцій$M,\ N$. Тоді ми шукаємо$C^1$ -функцію$\mu(x,y)$ таку, яка$\mu Mdx+\mu Ndy$ є загальним диференціалом, тобто., що$(\mu M)_y=(\mu N)_x$ задовольняється. Це лінійне рівняння з частинними похідними першого порядку для$\mu$:
$$
M\ mu_y-n\ mu_x=\ mu (n_x-m_y).
\]

Приклад 1.1.5:

Дві$C^1$ -функції$u(x,y)$ і$v(x,y)$ вважаються функціонально залежними, якщо
$$
\ det\ left (\ begin {array} {cc} u_x&u_y\\ v_x&v_y\ end {array}\ right) =0,
$$,
що є лінійним рівнянням з частинними похідними першого порядку для$u$ if$v$ є заданою$C^1$ -функцією. Великий клас розв'язків задається
$$
u=H (v (x, y)),
$$
де$H$ довільна$C^1$ -функція.

Приклад 1.1.6: Рівняння Коші-Рімана

Набір$f(z)=u(x,y)+iv(x,y)$, де$z=x+iy$ і$u,\ v$ задані$C^1(\Omega)$ -функції. $\Omega$Ось домен в$\mathbb{R}^2$. Якщо функція$f(z)$ диференційовна відносно комплексної змінної,$z$ то$u,\ v$ задовольняють рівняння Коші-Рімана
$$
u_x=v_y,\\ u_y=-v_x.
$$ З теорії функцій однієї комплексної змінної
відомо, що дійсна частина$u$ та уявна частина$v$ диференційовної функції$f(z)$ є розв'язками рівняння Лапласа
$$
\ трикутник u=0,\\ трикутник v=0,
$$
де$\triangle u= u_{xx}+u_{yy}$.

Приклад 1.1.7: Потенціал Ньютона

Потенціал Ньютона
$$
u=\ frac {1} {\ sqrt {x^2+y^2+z^2}
$
є розв'язком рівняння Лапласа в$\mathbb{R}^3\setminus{(0,0,0)}$, тобто

$u_ {xx} +u_ {yy} +u_ {zz} =0.
\]

Приклад 1.1.8: Рівняння теплоти

$u(x,t)$Дозволяти бути температура точки$x\in\Omega$ в той час$t$, де$\Omega\subset\mathbb{R}^3$ є домен. Потім$u(x,t)$ задовольняє в$\Omega\times[0,\infty)$ рівнянні
теплопровідності $$
u_t=k\ трикутник u,
$$
де$\triangle u= u_{x_1x_1}+u_{x_2x_2}+u_{x_3x_3}$ і$k$ є додатною константою. Умова
$$
u (x,0) =u_0 (x),\\ x\ in\ Omega,
$$
де задано,$u_0(x)$ є початковою умовою, пов'язаною з вищевказаним рівнянням теплоти. Умова
$$
u (x, t) =h (x, t),\\ x\ in\ partial\ Omega,\ t\ ge0,
$$
де$h(x,t)$ задано, є граничною умовою для рівняння теплоти.

Якщо$h(x,t)=g(x)$,$h$ тобто, не залежить від$t$, то можна очікувати, що рішення$u(x,t)$ прагне до функції$v(x)$ if$t\to\infty$. Більш того, виходить, що$v$ є розв'язком крайової задачі для рівняння Лапласа
\ begin {eqnarray*}
\ трикутника v&=&0\\\ mbox {in}\\ Omega\
v&=&g (x)\\\ mbox {on}\\ partial\ Omega.
\ end {еканаррей*}

Приклад 1.1.9: Хвильове рівняння

$альт$
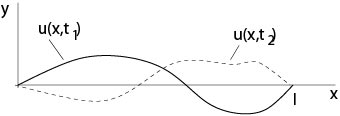
Малюнок 1.1.2: Коливальна струна

Хвильове рівняння
$$
u_ {tt} =c^2\ трикутник u,
$$
де$u=u(x,t)$,$c$ є додатною константою, описує коливання мембран або тривимірних областей, наприклад. В одновимірному випадку
$$
u_ {tt} =c^2 u_ {xx}
$$
описує коливання рядка.

Пов'язаними початковими умовами є
$$
u (x,0) =u_0 (x),\\ u_t (x,0) =u_1 (x),
$$
де$u_0,\ u_1$ задані функції. Таким чином прописується початкове положення і початкова швидкість.

Якщо рядок скінченний, то додатково описується граничні умови, наприклад
$$
u (0, t) =0,\ u (l, t) =0\\ mbox {for all}\ t\ ge 0.
\]