0,2: Вступ до диференціальних рівнянь

Диференційні рівняння

Закони фізики, як правило, записуються як диференціальні рівняння. Тому вся наука і техніка певною мірою використовують диференціальні рівняння. Розуміння диференціальних рівнянь має важливе значення для розуміння майже все, що ви будете вивчати у ваших наукових та інженерних класах. Ви можете думати про математику як про мову науки, а диференціальні рівняння є однією з найважливіших частин цієї мови, що стосується науки та техніки. Як аналогію, припустимо, що всі ваші заняття відтепер були дані суахілі. Було б важливо спочатку вивчити суахілі, інакше вам буде дуже важко отримати хорошу оцінку на ваших заняттях.

Ви бачили багато диференціальних рівнянь вже, можливо, не знаючи про це. І ви навіть вирішували прості диференціальні рівняння, коли ви брали обчислення. Давайте подивимося приклад, який ви, можливо, не бачили:\[\label{eq:1} \frac{dx}{dt} + x = 2 \cos t . \]\(x\) Ось залежна змінна і\(t\) незалежна змінна. Рівняння\(\eqref{eq:1}\) є базовим прикладом диференціального рівняння. Це приклад диференціального рівняння першого порядку, оскільки воно включає лише першу похідну залежної змінної. Це рівняння виникає з закону Ньютона охолодження, де температура навколишнього середовища коливається з часом.

Рішення диференціальних рівнянь

Розв'язування диференціального рівняння означає знаходження\(x\) в терміні\(t\). Тобто, ми хочемо, щоб знайти функцію\(t\), який ми називаємо\(x\), такий, що коли ми підключаємо\(x\)\(t\)\(\eqref{eq:1}\), і\(\frac{dx}{dt}\) в, рівняння тримає; тобто, ліва сторона дорівнює правій стороні. Це та ж ідея, що і для нормального (алгебраїчного) рівняння справедливого\(x\) і\(t\). Ми стверджуємо, що\[x = x(t) = \cos t + \sin t \nonumber \] це рішення. Як ми перевіряємо? Ми просто\(x\) підключаємо до рівняння\(\eqref{eq:1}\)! Для початку нам потрібно обчислити\(\frac{dx}{dt}\). Ми знаходимо це\(\frac{dx}{dt} = -\sin t + \cos t\). Тепер обчислимо ліву частину\(\eqref{eq:1}\). \[\frac{dx}{dt} + x = \underbrace{(-\sin t + \cos t)}_{\frac{dx}{dt}} + \underbrace{(\cos t + \sin t)}_{x} = 2\cos t . \nonumber \]Ура! У нас вийшла саме права сторона. Але є ще! Ми стверджуємо\(x = \cos t + \sin t + e^{-t}\), що це також рішення. Давайте\[\frac{dx}{dt} = -\sin t + \cos t - e^{-t} . \nonumber \] спробуємо, Ми підключаємося до лівої сторони\(\eqref{eq:1}\)\[\frac{dx}{dt} + x = \underbrace{(-\sin t + \cos t - e^{-t})}_{\frac{dx}{dt}} + \underbrace{(\cos t + \sin t + e^{-t})}_{x} = 2\cos t . \nonumber \] і він працює ще раз!

Так що може бути багато різних рішень. Для цього рівняння всі розв'язки можна записати у вигляді\[x = \cos t + \sin t + C e^{-t} , \nonumber \] для якоїсь константи\(C\). Різні константи\(C\) дадуть різні рішення, тому можливих рішень дійсно нескінченно багато. Див. Рисунок\(\PageIndex{1}\) для графіка декількох з цих рішень. Ми побачимо, як ми знаходимо ці рішення через кілька лекцій відтепер.

Малюнок\(\PageIndex{1}\): Мало рішень\(\frac{dx}{dt}+x=2\cos t\).

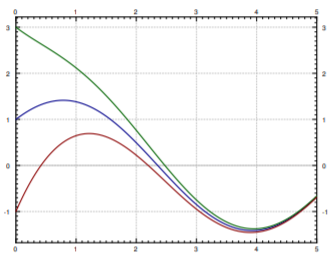
Розв'язування диференціальних рівнянь може бути досить важко. Не існує загального методу, який вирішує кожне диференціальне рівняння. Ми, як правило, зосередимося на тому, як отримати точні формули для розв'язків певних диференціальних рівнянь, але ми також витратимо трохи часу на отримання приблизних розв'язків. І ми витратимо деякий час на розуміння рівнянь без їх вирішення.

Велика частина цієї книги присвячена звичайним диференціальним рівнянням або ОДУ, тобто рівнянням тільки з однією незалежною змінною, де похідні є тільки по відношенню до цієї однієї змінної. Якщо незалежних змінних кілька, то отримуємо рівняння з частинними похідними або PDE.

Навіть для ОДУ, які дуже добре розуміються, це не просте питання повороту кривошипа, щоб отримати відповіді. Коли можна знайти точні рішення, вони, як правило, краще, ніж приблизні рішення. Важливо розуміти, як такі рішення знаходять. Хоча в реальних додатках ви залишите більшу частину фактичних обчислень комп'ютерам, вам потрібно розуміти, що вони роблять. Часто необхідно спростити або перетворити ваші рівняння в те, що комп'ютер може зрозуміти і вирішити. Можливо, вам навіть доведеться зробити певні припущення та зміни у вашій моделі, щоб досягти цього.

Щоб бути успішним інженером або вченим, вам потрібно буде вирішити проблеми у своїй роботі, яких ви ніколи раніше не бачили. Важливо вивчити методи вирішення проблем, так що ви можете застосувати ці методи до нових проблем. Поширеною помилкою є очікувати, щоб дізнатися якийсь рецепт для вирішення всіх проблем, з якими ви зіткнетеся у вашій подальшій кар'єрі. Цей курс не є винятком.

Диференціальні рівняння на практиці

Малюнок\(\PageIndex{2}\)

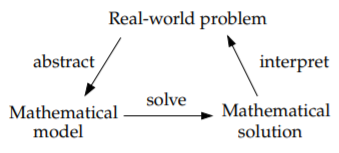
Отже, як ми використовуємо диференціальні рівняння в науці та техніці? По-перше, у нас є якась реальна проблема, яку ми хочемо зрозуміти. Зробимо кілька спрощуючих припущень і створюємо математичну модель. Тобто ми переводимо реальну ситуацію в сукупність диференціальних рівнянь. Потім ми застосовуємо математику, щоб отримати якесь математичне рішення. Залишилося ще щось зробити. Ми повинні інтерпретувати результати. Ми повинні з'ясувати, що математичне рішення говорить про реальну проблему, з якої ми почали.

Навчання формулювати математичну модель та як інтерпретувати результати - це те, що роблять ваші заняття з фізики та інженерії. У цьому курсі ми зосередимося здебільшого на математичному аналізі. Іноді ми будемо працювати з простими реальними прикладами, щоб мати певну інтуїцію та мотивацію щодо того, що ми робимо.

Давайте розглянемо на прикладі цього процесу. Одним з найбільш основних диференціальних рівнянь є стандартна експоненціальна модель зростання. \(P\)Позначимо популяцію деяких бактерій на чашці Петрі. Припускаємо, що є достатньо їжі і достатньо місця. Тоді швидкість росту бактерій пропорційна популяції — велика популяція зростає швидше. Нехай\(t\) позначають час (скажімо в секундах) і\(P\) чисельність населення. Наша модель є\[\frac{dP}{dt} = kP , \nonumber \] для деякої позитивної константи\(k > 0\).

Приклад\(\PageIndex{1}\)

Припустимо, що є\(100\) бактерії в той час,\(0\) а\(200\) бактерії через\(10\) секунди. Скільки бактерій буде\(1\) хвилина від часу\(0\) (в\(60\) секундах)?

Малюнок\(\PageIndex{2}\): Зростання бактерій в перші\(60\) секунди.

Рішення

Для початку нам потрібно вирішити рівняння. Ми стверджуємо, що рішення\(C\) дається\[P(t) = C e^{kt} , \nonumber \] де константа. Спробуємо:\[\frac{dP}{dt} = C k e^{kt} = k P . \nonumber \] І це дійсно рішення.

Гаразд, тепер що? Ми не знаємо\(C\), і не знаємо\(k\). Але ми щось знаємо. Ми знаємо\(P(0) = 100\), і знаємо\(P(10) = 200\). Давайте підключимо ці умови і подивимося, що станеться. \[\begin{align}\begin{aligned} & 100 = P(0) = C e^{k0} = C ,\\ & 200 = P(10) = 100 \, e^{k10} .\end{aligned}\end{align} \nonumber \]Тому\(2 = e^{10k}\) або\(\frac{\ln 2}{10} = k \approx 0.069\). Так що\[P(t) = 100 \, e^{(\ln 2) t / 10} \approx 100 \, e^{0.069 t} . \nonumber \] в одну хвилину\(t=60\), населення є\(P(60) = 6400\). Див\(\PageIndex{2}\). Малюнок.

Поговоримо про інтерпретацію результатів. Чи означає наше рішення, що на тарілці повинні бути саме\(6400\) бактерії\(60\text{s}\)? Ні! Ми зробили припущення, які можуть бути не вірними точно, приблизно. Якщо наші припущення обгрунтовані, то там будуть приблизно\(6400\) бактерії. Також в реальному житті\(P\) це дискретна величина, а не дійсне число. Однак наша модель не має проблем сказати, що, наприклад, в\(61\) секундах,\(P(61) \approx 6859.35\).

Зазвичай,\(k\) in\(P' = kP\) відомо, і ми хочемо вирішити рівняння для різних початкових умов. Що це означає? Візьміть\(k=1\) для простоти. Припустимо, ми хочемо вирішити рівняння, яке\(\frac{dP}{dt} = P\) підлягає\(P(0) = 1000\) (початкова умова). Тоді розчин виходить (вправа)\[P(t) = 1000 \, e^t . \nonumber \]

Ми\(P(t) = C e^t\) називаємо загальним рішенням, оскільки кожне рішення рівняння може бути записано в такому вигляді для деякої константи\(C\). Нам потрібна початкова умова, щоб з'ясувати, що\(C\) таке, щоб знайти конкретне рішення, яке ми шукаємо. Як правило, коли ми говоримо «конкретне рішення», ми просто маємо на увазі якесь рішення.

фундаментальні рівняння

Кілька рівнянь з'являються часто, і корисно просто запам'ятати, які їх рішення. Назвемо їх чотирма фундаментальними рівняннями. Їх рішення досить легко здогадатися, згадуючи властивості експоненціальних чисел, синусів і косинусів. Їх також просто перевірити, що ви завжди повинні робити. Не потрібно шукати відповіді на запитання, чи правильно ви запам'ятали рішення.

Спочатку таке рівняння є\[\frac{dy}{dx} = k y , \nonumber \] для деякої константи\(k > 0\). Тут\(y\) знаходиться залежна і\(x\) незалежна змінна. Загальне рішення для цього рівняння\[y(x) = C e^{kx} . \nonumber \] Ми бачили вище, що ця функція є рішенням, хоча ми використовували різні імена змінних.

Далі,\[\frac{dy}{dx} = -k y , \nonumber \] для якоїсь постійної\(k > 0\). Загальним рішенням для цього рівняння є\[y(x) = C e^{-kx} . \nonumber \]

Вправа\(\PageIndex{1}\)

Переконайтеся, що\(y\) дане дійсно є рішенням рівняння.

Далі візьміть диференціальне рівняння другого порядку\[\frac{d^2y}{{dx}^2} = -k^2 y , \nonumber \] для деякої константи\(k > 0\). Загальним рішенням для цього рівняння є\[y(x) = C_1 \cos(kx) + C_2 \sin(kx) . \nonumber \] Оскільки рівняння є диференціальним рівнянням другого порядку, ми маємо дві константи в нашому загальному рішенні.

Вправа\(\PageIndex{2}\)

Переконайтеся, що\(y\) дане дійсно є рішенням рівняння.

Нарешті, розглянемо диференціальне рівняння другого порядку\[\frac{d^2y}{{dx}^2} = k^2 y , \nonumber \] для деякої константи\(k > 0\). Загальним рішенням для цього рівняння є\[y(x) = C_1 e^{kx} + C_2 e^{-kx} , \nonumber \] або\[y(x) = D_1 \cosh(kx) + D_2 \sinh(kx) . \nonumber \]

Для тих, що не знають,\(\cosh\) і\(\sinh\) визначаються\[\cosh x = \frac{e^{x} + e^{-x}}{2} , \qquad \sinh x = \frac{e^{x} - e^{-x}}{2} . \nonumber \] Вони називаються гіперболічним косинусом і гіперболічним синусом. З цими функціями іноді легше працювати, ніж експоненціальні показники. Вони мають деякі приємні звичні властивості\(\cosh 0 = 1\), такі як\(\sinh 0 = 0\), і\(\frac{d}{dx} \cosh x = \sinh x\) (ні, що не є помилкою) і\(\frac{d}{dx} \sinh x = \cosh x\).

Вправа\(\PageIndex{3}\)

Переконайтеся, що обидві форми\(y\) заданого дійсно є розв'язками рівняння.

Приклад\(\PageIndex{2}\)

У рівняннях вищого порядку ви отримуєте більше констант, які ви повинні вирішити, щоб отримати конкретне рішення. Рівняння\(\frac{d^2y}{dx^2} = 0\) має загальне рішення\(y = C_1 x + C_2\); просто інтегруйте двічі і не забувайте про константу інтеграції. Розглянемо початкові умови\(y(0) = 2\) і\(y'(0) = 3\). Ми підключаємо наше загальне рішення і вирішуємо для констант:\[2 = y(0) = C_1 \cdot 0 + C_2 = C_2, \qquad 3 = y'(0) = C_1 . \nonumber \] Іншими словами,\(y = 3x + 2\) це конкретне рішення, яке ми шукаємо.

Цікава примітка про\(\cosh\): Графік\(\cosh\) - це точна форма висить ланцюга. Така форма називається контактної. Всупереч поширеній думці це не парабола. Якщо ви інвертуєте графік\(\cosh\), це також ідеальна арка для підтримки своєї ваги. Наприклад, арка шлюзу в Сент-Луїсі - це перевернутий графік\(\cosh\) - якби це була лише парабола, вона може впасти. Формула, яка використовується при проектуванні, вписана всередину арки:\[y = -127.7 \; \textrm{ft} \cdot \cosh({x / 127.7 \; \textrm{ft}}) + 757.7 \; \textrm{ft} . \nonumber \]