1.14: Комплексні числа
- Page ID
- 61349
Переглянути підручник на YouTube: складні числа
Переглянути підручник на YouTube: Складна експоненціальна функція
Ми визначаємо уявне число\(i\) як одне з двох чисел, яке задовольняє правилу\((i)^2 = −1\), інше число є\(−i\). Формально пишемо\(i =\sqrt{−1}\). Комплексне число\(z\) записується як\[z=x+iy,\nonumber\] де\(x\) і\(y\) є дійсними числами. \(x\)Називаємо реальну частину\(z\) і\(y\) уявну частину і пишемо\[x=\text{Re }z,\quad y=\text{Im }z.\nonumber\]
Два комплексних числа рівні тоді і тільки тоді, коли їх дійсна і уявна частини рівні.
Складний сполучений з\(z = x + iy\), позначається як\(\overline{z}\), визначається як\[\overline{z}=x-iy.\nonumber\]
Використовуючи\(z\) і\(\overline{z}\), у нас є\[\label{eq:1}\text{Re }z=\frac{1}{2}(z+\overline{z}),\quad\text{Im }z=\frac{1}{2i}(z-\overline{z}).\]
Крім того,\[\begin{aligned}z\overline{z}&=(x+iy)(x-iy) \\ &=x^2-i^2y^2 \\ &=x^2+y^2;\end{aligned}\] і ми визначаємо абсолютну величину\(z\), також звану модулем\(z\), шляхом\[\begin{aligned} |z|&=(z\overline{z})^{1/2} \\ &=\sqrt{x^2+y^2}.\end{aligned}\]
Ми можемо складати, віднімати, множити і ділити комплексні числа, щоб отримати нові комплексні числа. З\(z = x + iy\) і\(w = s + it\), і\(x,\)\(y,\)\(s,\)\(t\) дійсні числа, ми маємо\[ z + w = (x + s) + i(y + t);\quad z − w = (x − s) + i(y − t);\nonumber\]
\[\begin{aligned} zw&=(x+iy)(s+it) \\ &=(xs-yt)+i(xt+ys); \\ & \\ \frac{z}{w}&=\frac{z\overline{w}}{w\overline{w}} \\ &=\frac{(x+iy)(s-it)}{s^2+t^2} \\ &=\frac{(xs+yt)}{s^2+t^2}+i\frac{(ys-xt)}{s^2+t^2}.\end{aligned}\]
Крім того,\[\begin{aligned} |zw|&=\sqrt{(xs-yt)^2+(xt+ys)^2} \\ &=\sqrt{(x^2+y^2)(s^2+t^2)} \\ &=|z||w|;\end{aligned}\] і\[\begin{aligned}\overline{zw}&=(xs-yt)-i(xt+ys) \\ &=(x-iy)(s-it) \\ &=\overline{z}\overline{w}.\end{aligned}\]
Аналогічно\[\left|\frac{z}{w}\right| =\frac{|z|}{|w|},\quad\overline{\left(\frac{z}{w}\right)}=\frac{\overline{z}}{\overline{w}}.\nonumber\]
Крім того,\(\overline{z + w} = \overline{z} + \overline{w}\). \(|z + w| ≤ |z| + |w|\)Однак теорема відома як нерівність трикутника.
Особливо цікаво і корисно розглянути експоненціальну функцію уявного аргументу. Використовуючи розширення рядів Тейлора експоненціальної функції, ми маємо\[\begin{aligned}e^{i\theta}&=1+(i\theta )+\frac{(i\theta )^2}{2!}+\frac{(i\theta )^3}{3!}+\frac{(i\theta )^4}{4!}+\frac{(i\theta )^5}{5!}\cdots \\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\cdots\right)+i\left(\theta -\frac{\theta^3}{3!}+\frac{\theta^5}{5!}+\cdots\right) \\ &=\cos\theta +i\sin\theta.\end{aligned}\]
Оскільки ми визначили, що\[\label{eq:2}\cos\theta=\text{Re }e^{i\theta },\quad\sin\theta =\text{Im }e^{i\theta },\] ми також використовуємо\(\eqref{eq:1}\) і\(\eqref{eq:2}\), часто використовувані вирази\[\cos\theta =\frac{e^{i\theta}+e^{-i\theta }}{2},\quad\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}.\nonumber\]
Значна ідентичність Ейлера походить\(e^{iθ} = \cos θ + i \sin θ\) від встановлення\(θ = π\) та використання\(\cos π = −1\) та\(\sin π = 0\):
\[e^{i\pi}+1=0,\nonumber\]і ця ідентичність пов'язує п'ять основних чисел\(π\) -\(0,\: 1,\: i,\: e\) і - використовуючи три основні математичні операції - додавання, множення та зведення в ступінь - лише один раз.
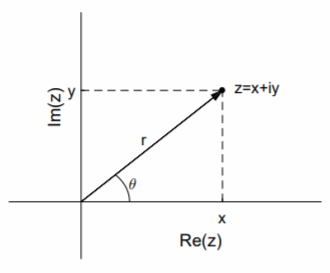
Комплексне число\(z\) може бути представлено в комплексній площині з\(\text{Re }z\) як\(x\) -вісь і\(\text{Im }z\) як\(y\) -вісь (див. Рис.\(\PageIndex{1}\)). Це призводить до полярного представлення\(z = x + iy\):
\[z=re^{i\theta},\nonumber\]де\(r = |z|\) і\(\tan θ = y/x\). Визначаємо\(\text{arg }z = θ\). Зверніть увагу, що не\(θ\) є унікальним, хоча прийнято вибирати значення таке\(−π < θ ≤ π\), що і\(θ = 0\) коли\(r = 0\).
Полярна форма комплексного числа може стати в нагоді при множенні чисел. Наприклад, якщо\(z_1=r_1e^{i\theta _1}\) і\(z_2=r_2e^{i\theta _2}\), то\(z_1z_2 = r_1r_2e^{i(θ_1+θ_2)}\). Зокрема, якщо\(r_2 = 1\), то множення\(z_1\) на\(z_2\) спини подання в\(z_1\) комплексній площині кута\(θ_2\) проти годинникової стрілки.
Корисні тригонометричні відносини можуть бути\(e^{iθ}\) виведені з використанням і властивостей експоненціальної функції. Закон додавання може бути отриманий від\[e^{i(x+y)}=e^{ix}e^{iy}.\nonumber\]
У нас є\[\begin{aligned} \cos(x + y) + i \sin(x + y) &= (\cos x + i \sin x)(\cos y + i \sin y) \\ &= (\cos x \cos y − \sin x \sin y) + i(\sin x \cos y + \cos x \sin y);\end{aligned}\] врожайність\[ \cos(x + y) = \cos x \cos y − \sin x \sin y,\quad \sin(x + y) = \sin x \cos y + \cos x \sin y.\nonumber\]
Теорема де Муавра походить від того\(e^{inθ} = (e^{iθ})^n\), що дає ідентичність\[\cos(nθ) + i \sin(nθ) = (\cos θ + i \sin θ)^n.\nonumber\]
Наприклад, якщо\(n=2\), виводимо\[\begin{aligned} \cos 2\theta +i\sin 2\theta &=(\cos\theta +i\sin\theta)^2 \\ &=(\cos^2\theta -\sin^2\theta)+2i\cos\theta\sin\theta.\end{aligned}\]
Тому,\[\cos 2θ = \cos^2 θ − \sin^2 θ,\quad \sin 2θ = 2 \cos θ \sin θ.\nonumber\]
Запишіть\(\sqrt{i}\) як стандартне комплексне число
Рішення
Щоб розв'язати цей приклад, спочатку потрібно визначити, що мається на увазі під квадратним коренем комплексного числа. Значення\(\sqrt{z}\) - це комплексне число, квадрат якого дорівнює\(z\). Таких чисел завжди буде два, тому що\((\sqrt{z})^2 = (−\sqrt{z})^2 = z\). Не можна визначити позитивний квадратний корінь, оскільки комплексні числа не визначаються як позитивні або від'ємні.
Ми покажемо два методи вирішення цієї проблеми. Перший найбільш простий метод пише\[\sqrt{i}=x+iy.\nonumber\]
Квадратуючи обидві сторони, ми отримуємо\[i=x^2-y^2+2xyi;\nonumber\] і прирівнюючи дійсну і уявну частини цього рівняння, виходить два дійсних рівняння\[x^2-y^2=0,\quad 2xy=1.\nonumber\]
Виходить перше рівняння\(y = ±x\). З\(y = x\), друге рівняння виходить\(2x^2 = 1\) з двома розв'язками\(x = ±\sqrt{2}/2\). З\(y = −x\), виходить друге рівняння\(−2x^2 = 1\), яке не має рішення для реального\(x\). Тому ми виявили, що\[\sqrt{i}=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
Другий метод розв'язку використовує полярну форму комплексних чисел. Алгебра, необхідна для цього методу, дещо простіша, особливо для знаходження кубових коренів, четвертих коренів тощо Ми знаємо\(i = e^{iπ/2}\), що, але загалом через періодичну природу полярного кута ми можемо записати,\[i=e^{i(\frac{\pi}{2}+2\pi k)},\nonumber\] де\(k\) є ціле число. Потім ми маємо\[\sqrt{i}=i^{1/2}=e^{i(\frac{\pi}{4}+\pi k)}=e^{i\pi k}e^{i\pi /4}=\pm e^{i\pi /4},\nonumber\], де ми використовували звичайні властивості експоненціальної функції, і\(e^{iπk} = ±1\) для\(k\) парних або непарних. Перетворення назад в стандартну форму, у нас є\[\sqrt{i}=\pm (\cos \pi /4+i\sin \pi /4)=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
Фундаментальна теорема алгебри стверджує, що кожне поліноміальне рівняння ступеня\(n\) має точно\(n\) складні коріння, підраховані з кратністю. Два знайомі приклади були б\(x^2 − 1 = (x + 1)(x − 1) = 0\), з двома коренями\(x_1 = −1\) і\(x_2 = 1\); і\(x^2 − 2x + 1 = (x − 1)^2 = 0\), з одним коренем\(x_1 = 1\) з кратністю два.
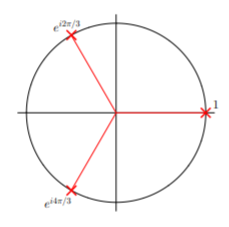
Задача знаходження коренів\(n\) одиниці полягає у розв'язанні поліноміального рівняння\[z^n=1\nonumber\] для\(n\) комплексних значень\(z\). У нас є\(z_1 = 1\) для\(n = 1\); і\(z_1 = 1\),\(z_2 = −1\) для\(n = 2\). Крім того\(n = 2\), деякі корені складні, і тут ми знаходимо кубічні корені єдності, тобто три значення\(z\) цього задовольняють\(z^3 = 1\). Запис\(1 = e^{i2πk}\), де\(k\) ціле число, ми маємо\[z=(1)^{1/3}=\left(e^{i2\pi k}\right)^{1/3}=e^{i2\pi k/3}=\left\{\begin{array}{l}1; \\ e^{i2\pi /3}; \\ e^{i4\pi /3}.\end{array}\right.\nonumber\]
\(\cos (2π/3) = −1/2,\)\(\sin (2π/3) = \sqrt{3}/2,\)\(\cos (4π/3) = −1/2,\)\(\sin (4π/3) = − \sqrt{3}/2,\)За допомогою трьох кубічних коренів одиниці задаються\[z_1=1,\quad z_2=-\frac{1}{2}+i\frac{\sqrt{3}}{2},\quad z_3=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.\nonumber\]
Ці три кореня рівномірно розташовані навколо одиничного кола в складній площині, як показано на малюнку нижче.