3.2: Набір проблем 3

Last updated
Save as PDF

Page ID: 59094

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Якщо не вказано інше, припустити всі аксіоми нейтральної геометрії (хоча і невизначеної) та глобальну форму гіперболічного паралельного постулату (ГЕС), а також; тобто припустити гіперболічну геометрію.

Доведіть, що сума внутрішніх кутів будь-якого трикутника менше двох прямих кутів$\left(180^{\circ}\right)$.
Не припускайте ГЕС, але припускайте, що існує один трикутник, для якого сума внутрішніх кутів менше$180^{\circ}$. Доведіть локальну форму ГЕС.
Не припускайте ГЕС, але припускайте, що існує одна пара паралельних ліній, які поділяють поперечну, яка утворює пару неконгруентних альтернативних внутрішніх кутів. Доведіть локальну форму ГЕС.
Доведіть, що вершина чотирикутника Сакхері ніколи не межа (межа) паралельно його основі.
Доведіть, що сторона чотирикутника Ламберта ніколи не межа (межа) паралельно його протилежній стороні.
Доведіть, що дві лінії не поділяють більше одного спільного перпендикуляра (тобто немає «залізничних колійних зв'язків»).

В Exs 7-10 розглянемо модель гіперболічної геометрії Пуанкаре в евклідовій геометрії, визначену окружністю радіуса 2 з центром у початку$\mathrm{O}(0,0)$ декартової площини,$\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<2^{2}\right\}$

7. Знайдіть рівняння для кола$\delta$, що визначає праву межу (межу), паралельну$\mathrm{x}$ -осі на точці,$\mathrm{P}(1,1)$ і точно накидайте ситуацію.

[Підказка: Центр цього кола повинен лежати на лінії$x=2$. Чому? Згадаймо рівняння кола з центром$\mathrm{C}(\mathrm{h}, \mathrm{k})$ і радіусом$\mathrm{r}: \delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.$.]

Повторити Ex 7 для лівої межі паралельно в тій же точці$P(1,1)$.
Зробіть точний ескіз ситуації в Exs 7 і 8 і «намалюйте» лінію Пуанкаре на$P(1,1)$ перпендикулярній$\mathrm{x}$ осі.
Знайдіть рівняння для$\delta$ евклідового кола прямої Пуанкаре в Ex 9. [Підказка: Для ортогональності з$\mathrm{x}$ -віссю його центр$\mathrm{C}$ повинен бути на$\mathrm{x}$ -осі, скажімо$(c, 0)$, рівняння, і воно проходить$\mathrm{P}(1,1)$.$(\mathrm{x}-\mathrm{c})^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$ Необхідною додатковою умовою є ортогональність з визначальним колом. Це можна легко зробити, використовуючи теорему Піфагора з радіусами і відстанню між центрами,$|c|$
Розглянемо модель Пуанкаре гіперболічної геометрії в евклідовій геометрії, визначену окружністю радіуса 4 з центром у початку$\mathrm{O}(0,0)$ декартової площини,$\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<4^{2}\right\}$. Знайти рівняння для$\delta$ евклідової окружності лінії Пуанкаре, визначеної точками$\mathrm{A}(1,2)$ і$\mathrm{B}(3,0)$.

[Підказка: Для його$\delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.$ рівняння ортогональність з визначальним колом може бути задіяна за допомогою теореми Піфагора:$4^{2}+r^{2}=h^{2}+k^{2}$ так що$r^{2}=h^{2}+k^{2}-4^{2}$. Перпендикулярна бісектриса евклідового відрізка AB має нахил 1, проходить через середину$\mathrm{M}(2,1)$, і (h, k).] 12. Ідея Ex 11 може бути узагальнена, щоб надати аналітичний доказ (див. Розділ. 4) Аксіоми 1 як теорему евклідової геометрії як один крок у доказі того, що модель Пуанкаре дійсно є моделлю гіперболічної геометрії повністю в межах евклідової геометрії (встановлення «відносної узгодженості» гіперболічної геометрії аксіоми (див. Розділ 5 для тривіального синтетичного доказу!). Розглянемо модель Пуанкаре, визначену окружністю радіуса,$\mathrm{R}$ зосередженою на початку$\mathrm{O}(0,0)$ декартової площини,$\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<\mathrm{R}^{2}\right\}$.

Знайдіть рівняння для$\delta$ евклідової окружності лінії Пуанкаре, визначеного двома загальними точками Пуанкаре$\mathrm{A}\left(\mathrm{a}_{\mathrm{x}}, \mathrm{a}_{\mathrm{y}}\right)$ і$\mathrm{B}\left(\mathrm{b}_{\mathrm{x}}, \mathrm{b}_{\mathrm{y}}\right)$ де$\mathrm{A}, \mathrm{B}$, і$\mathrm{O}$ не колінеарні.

Тобто, якщо$(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}$ є його рівнянням, експресом$\mathrm{h}, \mathrm{k}$, і r однозначно за термінами$\mathrm{R}$ і координатами$A$ і B. Ортогональність з визначальним колом може бути задіяна за допомогою теореми Піфагора:

$\mathrm{R}^{2}+\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}$так що$\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}$. Перпендикулярна бісектриса евклідового відрізка AB повинна пройти через його середину$\mathrm{M}$ та центр кола$\mathrm{C}(\mathrm{h}, \mathrm{k})$. Три випадки трапляються з найбільш загальним тим, що евклідова лінія не$A B$ є ні вертикальною, ні горизонтальною. У цьому випадку обчислити рівняння перпендикулярної бісектриси,$\mathrm{y}=\mathrm{mx}+\mathrm{b}$ з$\mathrm{m}$ тим, що є негативним зворотним нахилу лінії AB і використовуючи$M$ для обчислення b Оскільки$C$ знаходиться на цій лінії, ми маємо$k=m h+b$ і, підставляючи в координати або А або$\mathrm{B}$ те, що повинно лежати на колі, ми будемо мати$(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}$ цілком в плані$\mathrm{h}($ і задані коефіцієнти). На щастя, терміни, пов'язані з$h^{2}$ скасуванням, і ми можемо вирішити однозначно для ч, потім$\mathrm{k}=\mathrm{mh}+\mathrm{b}$, і нарешті$\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}$. Тобто існує одне і тільки одне таке коло. Інші два випадки використовують ту саму ідею, але простіші.

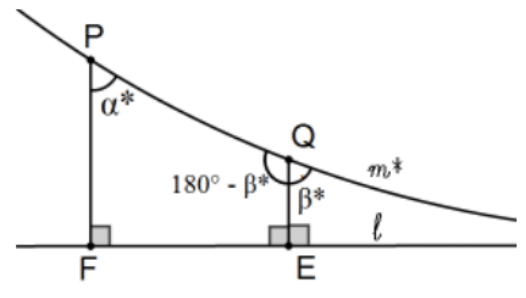
$Знімок екрана 2022-06-25 в 1.17.15 PM.png$

13. Довести, що кути паралелізму строго збільшуються вздовж граничних паралелей у напрямку обмеженості.

[Підказка: Дана цифра говорить про все:$\alpha^{*}+\left(180-\beta^{*}\right)<180^{\circ}$ тому що PQEF є чотирикутником.]

Багатокутник може бути описаний, якщо існує коло, яке називається circurcircle, яке містить кожну вершину багатокутника. Повинно бути очевидним, що багатокутник можна описати, якщо є точка, рівновіддалена від кожної його вершини.

14. Доведіть, що чотирикутник Ламберта ніколи не може бути обмежений. [Підказка: Припустімо, що існує коло кола і вивести протиріччя; тобто використовувати докази протиріччя. Примітка: Не припускайте, що перетин діагоналей є центром передбачуваного кола, але ви можете використовувати той факт, що він повинен мати центр.]

Побудувати окружність чотирикутника Сакхері. [Підказка: Побудувати перпендикулярні бісектриси катета і підстави і довести, що перетин рівновіддалений від кожної з вершин, отже, центр окружності.]
Доповніть доказ того, що трикутники останньої теореми глави є справжніми трикутниками і що їх неможливо обмежити. [Чому презентація виходить з ладу в евклідовій геометрії?]
Покажіть ретельним ескізом у площині Пуанкаре, що не всі трикутники можна обмежити, і аргументуйте, чому його не можна обмежити. Аргумент Пуанкаре? Евклідовий аргумент?

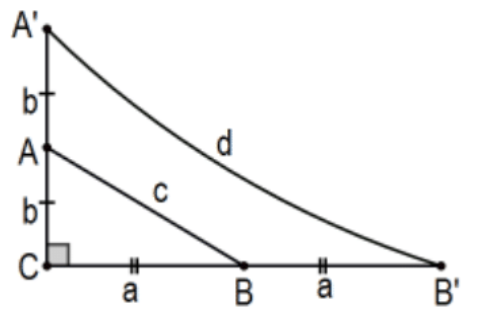
$Знімок екрана 2022-06-25 в 1.19.32 PM.png$

18. Доведіть, що теорема Піфагора не вдається, показуючи, що якщо$\triangle \mathrm{ABC}$ це прямокутний трикутник з$\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}$, то прямокутний трикутник з ніжками 2а і$2 \mathrm{~b}$ не задовольняє рівняння Піфагора.

[Підказка: Розглянемо асоційований чотирикутник Сакхері з вершиною A${ }^{\prime} \mathrm{B}^{\prime}$.]

19. Доведіть теорему саміту.

20. Теорема: Якщо два чотирикутника Сакері мають конгруентні основи та конгруентні вершини, то вони є конгруентними. [Тобто доведіть це.]

У Ex 21-24 припустимо, що A і B - це точки всередині фіксованого евклідієвого кола$\gamma$, що визначає модель диска Пуанкаре для гіперболічної геометрії,$\delta$ це ортогональне коло, визначене A і$\mathrm{B}$,$\mathrm{P}$ і$\mathrm{Q}$ точки перетину кіл$\gamma$ і$\delta$. Нагадаємо, що відстань Пуанкаре між точками A і B (міра відрізка лінії Пуанкаре AB) становить:

\[m_{p}(A B)=d_{p}(A, B)=|\ln (A, B ; P, Q)|=\left |\ln \left(\frac{A P / P B}{A Q / Q B} \right) \right|= \left| \ln \left(\frac{(A P)(Q B)}{(A Q)(P B)}\right) \right|. \nonumber\]

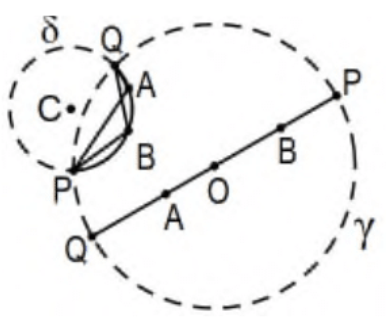
$Знімок екрана 2022-06-25 в 1.20.46 PM.png$

де$P$ і$Q$ визначаються лінією Пуанкаре, визначеною$A$ і$B$.

21. Доведіть, що відстань Пуанкаре не залежить від того, яка точка позначена P, а яка - Q.

Доведіть, що$d_{p}(A, B)=d_{p}(B, A)$.
Доведіть, що$d_{p}(A, B)=0$ якщо$A=B$.
Доведіть$A, B$, що якщо, і$C$ є колінеарними точками в моделі Пуанкаре,$d_{p}(A, B)+d_{p}(B, C)=d_{p}(A, C)$ iff$\mathrm{B}$ знаходиться між A і C; тобто між ними на Пуанкаре частина (ж) Евклідова коло визначається будь-якими двома точками.

[Примітка 1: Не пропустіть найважливішу деталь, той факт, що$|\mathrm{x}|+|\mathrm{y}|$ не обов'язково дорівнює$|\mathrm{x}+\mathrm{y}|$ лише "$\geq$. Спочатку ви повинні підтвердити, що в будь-якій ситуації, яку ви використовуєте, рівність дотримується.]

[Примітка 2: Повне поняття «між» вимагає, щоб B був між A і C, це рівняння тримається без припущення, що точки будуть колінеарними. Це вірно для заходів Пуанкаре відрізків ліній, але доказ набагато складніший. Див. Розділ 5, завершуючи PS 5, #8.]

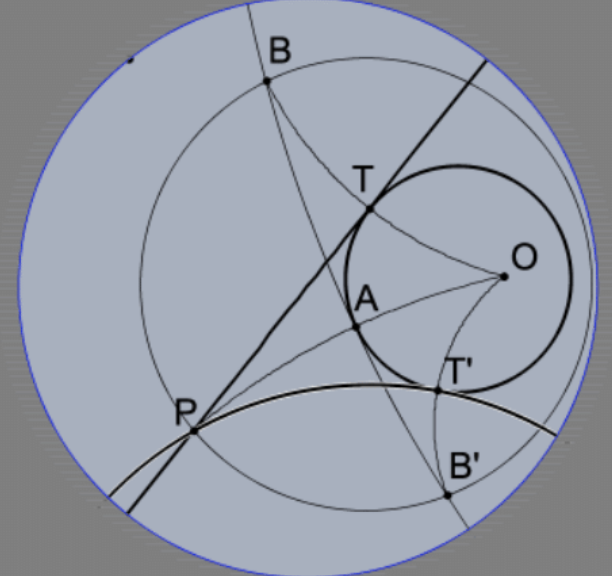
$Знімок екрана 2022-06-25 в 1.22.05 PM.png$

25. Припускаючи, що модель диска Пуанкаре дійсно є моделлю для гіперболічної геометрії, згадайте конструкцію для дотичних з точки Р поза окружністю O, заданої в PS 2, #28, і поясніть зазначену конструкцію дотичних ліній$\mathrm{PT}$ і$\mathrm{PT}^{\prime}$ до кола Пуанкаре (O; OA ) (тобто центр$\mathrm{O}$ радіуса OA) у зображеній моделі диска Пуанкаре (припускаючи, що «компас Пуанкаре» та «Poincaré straightedge») і довести, що конструкція дійсна. [Примітка1: Зрештою, ми включимо конструкцію дотичних Пуанкаре за допомогою «Евклідових інструментів» (набагато простіше прийти!) але це набагато складніше. Примітка 2: Кроки найвідомішої побудови цих дотичних в евклідовій геометрії можуть бути виконані за допомогою компаса Пуанкаре та прямолінійного краю в моделі диска Пуанкаре, але результат не правильний. Іншими словами, докази мають значення!]

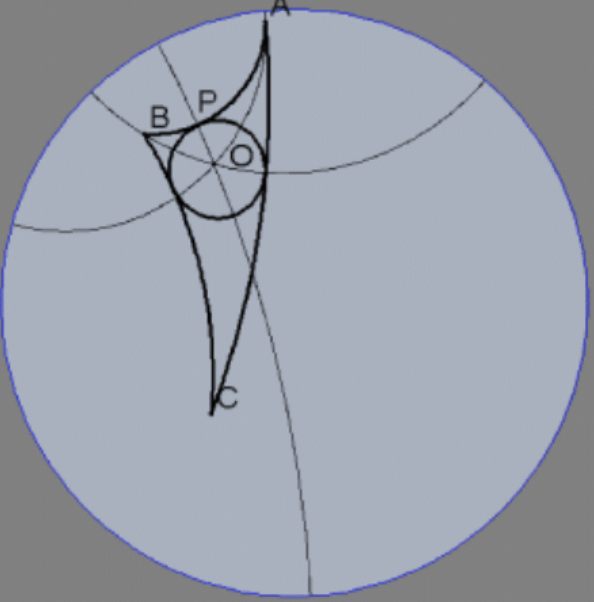
$Знімок екрана 2022-06-25 в 1.23.23 PM.png$

26. Припускаючи, що модель диска Пуанкаре дійсно є моделлю для гіперболічної геометрії, згадайте конструкцію для вписаного трикутника з глави 2 (нейтральна геометрія). Поясніть зазначену конструкцію вхідного кола даного трикутника у зображеній моделі диска Пуанкаре і доведіть, що вона дійсна.

[Примітка: Як і у випадку з Екс. 25, на малюнку конструкція використовує компас Пуанкаре і straightedge, але можна побудувати вписане коло трикутника Пуанкаре з евклідовим компасом і straightedge, але це надзвичайно нудно.]

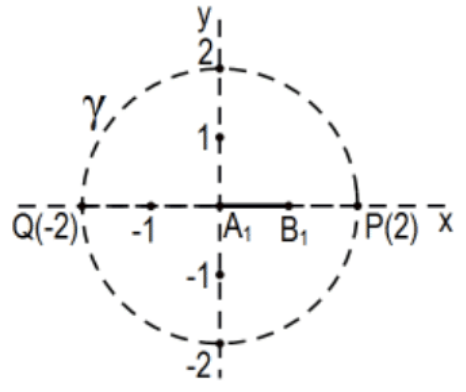
27а. Відрізок$\mathrm{A}_{1} \mathrm{~B}_{1}=[0,1]=\{\mathrm{x} \in \mathbf{R} \mid 0 \leq \mathrm{x} \leq 1\}$ має евклідову міру 1 (сюрприз, сюрприз). Підтвердьте, що його міра Пуанкаре знаходиться$\ln (3)$ в моделі Пуанкаре,$\gamma=(\mathrm{O} ; 2)$ визначеній, пояснивши цей розрахунок:

$\mathrm{m}_{f}([0,1])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{2 / 1}{2 / 3}\right)\right|=\left|\ln \left(\frac{3}{1}\right)\right|=|\ln (3)|=\ln (3)$

$Знімок екрана 2022-06-25 в 1.24.39 PM.png$

27б. Зробіть те ж саме для сегмента$\mathrm{A}_{2} \mathrm{~B}_{2}=[1,3 / 2]$; тобто обчислити як його евклідові, так і пуанкаре заходи.

27c. Те ж саме виконайте для сегмента$\mathrm{A}_{3} \mathrm{~B}_{3}=[3 / 2,7 / 4]$.

27д. Те ж саме виконайте для сегмента$A_{n} B_{n}=\left[\left(2^{n-1}-1\right) / 2^{n-2},\left(2^{n}-1\right) / 2^{n-1}\right]$.

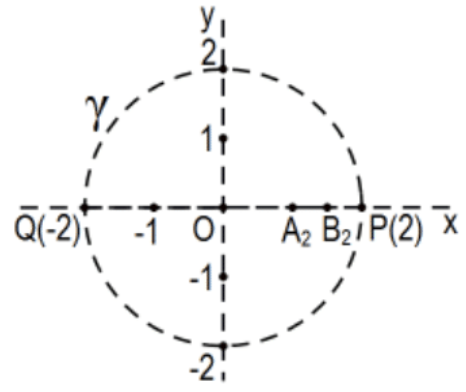
$Знімок екрана 2022-06-25 в 1.27.25 PM.png$

Що таке ліміт як$n \rightarrow \infty$?

Примітка: Сегменти типу$[0,1]$ в #27a вище особливо легко обчислити:

$[0, x]$Дозволяти Евклідова сегмент вздовж$x$ -осі, який також є відрізком у моделі Пуанкаре, визначеної колом$\gamma=(\mathrm{O} ; \mathrm{R})$, сегмент AB на малюнку,$0<\mathrm{x}<\mathrm{R}$. Зрозуміло, що його евклідова міра справедлива$\mathrm{x}$. Для його міри Пуанкаре: [Тут ми враховуємо напрямок, а також позитивну евклідову довжину.]

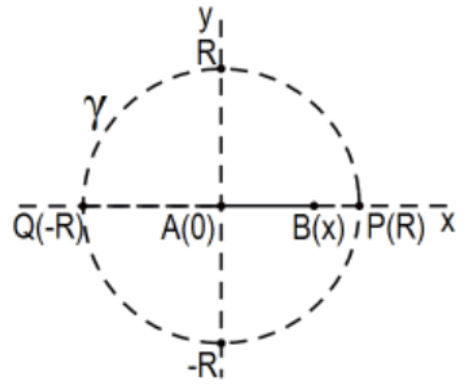
$Знімок екрана 2022-06-25 в 1.27.59 PM.png$

\[\mathrm{m}_{f}([0, \mathrm{x}])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{\mathrm{R} /(\mathrm{x}-\mathrm{R})}{-\mathrm{R} /(\mathrm{R}+\mathrm{x})}\right)\right|=\left|\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right)\right|=\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right) \nonumber\]

Note: The last expression makes it clear that, as $\mathrm{x}$ approaches $\mathrm{R}$, the length of segment [A(0), $\mathrm{B}(\mathrm{x})]$ becomes infinite (as it must). In Chapter 5 (PS 5, #5), we will see that by an easy isometric (congruence) transformation, the Poincaré measure of any Poincaré segment in a Poincaré model in the $\mathrm{x}$,y-coordinate (Cartesian) plane can be computed in this convenient manner, no simultaneous solution of two quadratic equations in two variables (to find the coordinates of the defining points $P$ and $Q$, and no Euclidean distance formula computations required.