Передмова

Вступ

Курс починається з огляду кількох найелементарніших результатів традиційної евклідової геометрії; насправді, тих, що були на початку Книги 1 Елементи, евклідового оригіналу. Так як цьому твору близько 2300 років, права на оригінал не є проблемою. Протягом тисячоліть математики переконалися, що споконвічні греки і покоління математиків, які слідували за ними, вважали, що «унікальність паралелей» можна довести з більш фундаментальних «аксіом» про геометрію (літ., «міра землі»), які були настільки очевидні, що їх можна сміливо припустити без доказів. Стандартний зміст курсу під назвою «Сучасна геометрія» передбачає доведення, що це не так, і вивчення того, що відбувається за іншим припущенням.

Розуміння того, що сучасні математики мають на увазі під «доказом», датується цією епохою і цим твором «Стихії». Багато з нас переконані, що з усіх внесків давніх греків в сучасну людську думку найважливішим є їх ідеї дедуктивної логіки, конкретизовані математичним доказом.

Там було багато книг, написаних і хороші підручники доступні, які охоплюють матеріал цього курсу. На жаль, книги, які йдуть досить глибоко, щоб розвивати предмет добре припускають рік навчання, семестру недостатньо, особливо для студентів зі слабким досвідом. Стандартний підхід полягає в тому, щоб спочатку розробити більше результатів передової евклідової геометрії і врешті-решт створити резервну копію і перейти в гіперболічну геометрію. Для того, щоб потрапити туди, куди нам потрібно потрапити, ми не будемо формально розробляти деякі передові евклідові результати, які логічно потрібні, тому що ми ніколи не дійдемо до «сучасної» частини назви курсу. Ми повернемося і розвиватимемо, або, принаймні, концептуально, деякі з них, коли вони нам знадобляться пізно в курсі. Значний компроміс з математичною формальністю буде принесений в жертву для досягнення цієї мети, але не сама ідея математичного доказу. Фактично, найважливішою метою курсу є зміцнення доказових тверджень в рамках установки евклідової геометрії. Те, що контекст не може бути «евклідовим», може бути дуже корисним для розуміння самого евклідового налаштування. Якщо ви ніколи не мали досвіду в евклідовій геометрії на основі доказів, очікуйте, що курс буде дуже складним, можливо, навіть занадто складним для вашого успіху без виняткових зусиль з вашого боку.

Передбачається, що ви володієте робочими знаннями елементарної логіки; наприклад, зручне використання універсальних тверджень («для кожного...» \(\forall\)) проти екзистенціальних тверджень («існує...» \(\exists\)) де кожен крапки, «...», сам по собі є твердженням. Це підтримує нас ще далі; що таке «заява»? Це речення (у нашому випадку англійська, але будь-яка мова буде робити), яке має «істинне значення»; має сенс називати його «true» або «false» на відміну від, скажімо, питань чи команд. Ці ідеї та набагато більш елементарна евклідова геометрія можуть сприйматися як належне до останніх кількох десятиліть, але, на жаль, це вже не так. Традиційний курс середньої школи, як правило, «геометрія другого курсу», дав зовсім інший фон, ніж багато студентів - навіть сильні студенти з математикою на основі кар'єрних прагнень - пережили. Я глибоко вірю, що такі студенти не змінюються цим «прогресом», але реальність така, якою вона є. Як конкретний приклад, одна з найкращих і найпопулярніших книг у проективній геометрії (включаючи цей кампус - використовуючи цю ж назву курсу та номер!) в новітній історії - це Лекції Зайденберга в проективній геометрії, з Університетської серії в математиці бакалаврату, 1962, D. Ван Ностранд компанії, Inc. з першого абзацу вступу:

«Мета цієї книги - надати текст для бакалаврату з проективної геометрії. Аксіоматичний підхід до цього предмета, безсумнівно, правильний, але здається бажаним, якщо не потрібно, відштовхуватися від того, що знає учень, а саме геометрії середньої школи, і виходити з нього звідти до нового. Відповідно, перша глава присвячена введенню деяких основних тем в максимально наївній формі».

Те, що «наївна форма, наскільки це можливо» першої глави, повинна служити попередженням. Я б кинув виклик більш ніж двом студентам в цьому класі, щоб прочитати і зрозуміти його без серйозної допомоги; можливо, половина нашого семестру повинна бути присвячена, щоб дістатися до підготовки UC Берклі Авраам Сейденберг мав на увазі для початку курсу. Якщо у вас не було досить традиційного курсу евклідової геометрії на основі доказів, пошук старшої середньої школи геометрії тексту або одного з деяких коледжів громади (багато з яких не втратили свій шлях) для вивчення може бути дуже корисним початком (як зараз!) для курсу. Ще одна можливість - це досить дивовижна безкоштовна онлайн-академія Хана, яка може запропонувати цей «огляд», який може бути набагато більше, ніж огляд, але необхідний для успіху в цьому курсі та для відповідного розуміння геометрії на основі доказів конкретно та математики на основі доказів загалом:

https://www.khanacademy.org/math/geometry/

Це перший рік, курс середньої школи з геометрії (який заснований на елементах Евкліда). Він переглядає багато основних геометричних концепцій, вивчених на попередніх курсах, але розглядає їх з більшою математичною строгістю. Існує сильна увага на доведенні теорем та результатів основних постулатів.

Продовжуючи (як і у всій формальній математиці), «твердження» - це речення, яке має невизначене «значення істини» (сподіваємось, значуще в контексті), а нові твердження будуються з існуючих кількома способами. Для одного твердження його заперечення означає будь-яку переформулювання твердження таким чином, що якщо воно було істинним, нове твердження є хибним і обернено, якщо воно було помилковим, нове твердження є істинним. Символічно, якщо\(p\) є твердженням, то його заперечення позначається\(\sim p\) або\(\neg p\) або, рідше,\(p^{\prime}\). Два або більше тверджень можуть бути складені в нові твердження кількома способами; найбільш очевидними є і/і/або (формально, кон'юнкція і диз'юнкція, які ми ніколи не будемо використовувати поза цим введенням разом з їх формальними логічними символами, \(\wedge\)і\(\vee\)). У першому випадку твердження є істинним тоді і лише тоді, коли обидва (усі, якщо більше двох) твердження є істинними, а в останньому - істинним, якщо і лише тоді, коли хоча б одне з них є істинним.

Повернувшись до універсальних та екзистенціальних тверджень, їх формальні назви рідко використовуватимуться, а формальні символи\((\forall\) і\(\exists\)) ніколи не використовуються. Також розуміється - але цей час часто використовується - буде думка про те, що для доказу того, що універсальне твердження помилкове вимагає лише показати один конкретний контрприклад (один приклад твердження, яке є демонстративно помилковим) або, як іноді більш просвітницьким, набір прикладів висловлювання з якесь спільне властивість, яке показує все (що важливо!) з них бути помилковими. Для нематематичного прикладу розглянемо твердження «Всі собаки білі». Очевидно, що це помилковий і єдиний контрприклад, показуючи одну коричневу (або будь-який колір (і), крім білого) собака доводить, що вона помилкова, як і набір всіх коричневих собак (оскільки цей набір непорожній). Один менш очевидний факт - але цілком стандартний у всій математиці - якщо інше не кваліфіковано, загальні твердження вважаються універсальними. Як приклад геометрії, «Рівносторонній трикутник рівнокутний» вважається твердженням про всі рівносторонні трикутники, а не лише деякі з них, інакше він повинен сказати щось на кшталт: «Якийсь рівносторонній трикутник рівносторонній», або еквівалентно: «Деякі рівносторонні трикутники рівносторонні», оскільки множинний прикметник «деякі» в логіці означає те ж саме, що і «один або кілька»; тобто «принаймні один».

Вже використовується у вступному абзаці, є «робочим знанням» умовних тверджень (також відомих як наслідки); тобто «Якщо..., то...» заяви, де кожне «...» є твердженням. Трохи більш формально\(p\), «Якщо\(q\), то», де\(p\) (попереднє) і\(q\) (наслідок) є твердженнями. У формальній логіці це написано\(p \Rightarrow q\) "" (або "\(p \rightarrow q\)«) і рідко використовуватиметься, за винятком тут, де зручніше переглядати відповідні терміни. По-перше, "\(p \Rightarrow q\)" є true, за винятком одного випадку, коли\(p\) true і\(q\) false. З цієї причини доведення наслідків здійснюється шляхом припущення, що\(p\) це правда, і доведення, що з цим припущенням також\(q\) має бути правдою. При першому знайомстві ця конвенція може здатися контрінтуїтивною, але логіка здорового глузду вимагає, щоб такі твердження, як «Якщо всі собаки білі, то моя собака біла», вважалися правдою, навіть якщо вона безглузда, тому що, очевидно, не всі собаки білі, але, незважаючи на попереднє буття. явно неправдиве, твердження потрібно вважати правдивим. Якщо ви не впевнені, що це твердження безглузде, розгляньте цю невелику модифікацію: «Якщо всі собаки білі, значить моя собака чорна». Знову ж таки, попереднє є помилковим, тому твердження вважається правдивим, але, очевидно, безглуздим.

[Примітка: Це з точки зору того, що відомо як «пропозиційна логіка». Такі («кількісні») твердження зазвичай розглядаються з точки зору того, що відомо як «логіка предикатів».]

Ви можете згадати з логіки, що таке імплікацію\(p \Rightarrow q\) "" логічно еквівалентно (тобто одне твердження істинно тоді і тільки тоді, коли інше твердження істинно) складеному твердженню "\((\sim p) \vee q\)", який є істинним, якщо або\(\sim p\) є істинним (тобто, \(p\)є помилковим) або\(q\) є істинним. Тобто, щоб початковий підтекст був істинним, або попереднє\(p\) є помилковим, або наслідком\(q\) є істинним, отже, еквівалентність. Якщо вам це не здається знайомим, легко довести такі твердження за допомогою таблиць істинності; тобто безпосередньо підтвердити всі можливі значення істинності, в даному випадку чотири.

Назад кілька абзаців, слово «обернено» було використано, хоча і менш обережно, але поширене використання могло сказати «навпаки». Ідея зворотного імплікації є критичною в цьому курсі та всієї математики, як і інші перестановки висловлювань, що беруть участь. З огляду на загальний підтекст:

Мається\(p \Rightarrow q\) на увазі: Перестановки:

зворотне:\(q \Rightarrow p\) Тобто, обмінюватися попереднім і наслідком.

зворотний:\(\sim p \Rightarrow \sim q\) Тобто, звести нанівець попереднє, а також наслідок.

контрапозитивний:\(\sim q \Rightarrow \sim p\) Тобто як заперечують, так і міняють попереднє та наслідкове.

Чи не перестановка оригіналу, а пов'язане твердження, яке може бути правдою або не може бути правдою:

\(p \Leftrightarrow q\)двозастережний: Тобто і підтекст, і його зворотне:\(p \Rightarrow q\) і\(q \Rightarrow p\).

Ви повинні знати (це легко довести), що початковий імплікація та його контрапозитив логічно еквівалентні (одне вірно тоді, коли інше істинно), як і його зворотне (контрапозитивний означає це). Нарешті, двозастережним є істинним, якщо і тільки тоді\(p\) і\(q\) є або істинними, або обома хибними.

Критичне значення має той факт, що підтекст і його зворотність за своєю суттю не є логічно еквівалентними (Якщо моя собака біла, то всі собаки білі?) хоча часто трапляється, що наслідки в математиці є двоумовними; тобто «якщо і тільки тоді» і скорочено як «iff» Наприклад, «Трикутник рівносторонній тоді і тільки тоді, коли він рівнокутний», або більш стисло, «Трикутник рівносторонній, якщо він рівнокутний». На перший погляд, таке твердження не схоже на будь-який підтекст, але вам потрібно рівноцінно і без зусиль думати про нього як: «Якщо трикутник рівнокутний, то він рівносторонній і навпаки; тобто, якщо трикутник рівносторонній, то він рівнокутний».

«Думай про це як» може здатися назад, але це не так. Якщо це незрозуміло, потрібно більш уважно вивчити позицію «якщо» і «тільки якщо» в заяві. Залиште «і тільки якщо», щоб легше побачити ідею. Символічно, що це скаже\(q\) "\(p\)якщо" це майже очевидно еквівалентно «якщо\(q\), то\(p\)». «Тільки якщо» спочатку трохи складніше зрозуміти, але подумайте про те, що «\(p\)тільки якщо\(q\)» має означати; це повинно означати, що\(q\) випливає з знання\(p\) або, якщо\(p\) це правда, то\(q\) також має бути правдою. Тобто якщо\(p\), то\(\mathrm{q}\). Звідси і еквівалентність.

Перші 28 пропозицій оригінальної Книги 1 Елементів Евкліда не використовують «Евкліда\(5^{\text {th }}\)», відомого як «Паралельний постулат», і ці пропозиції - це те, де ми розпочнемо курс. Ми будемо використовувати їх як огляд геометрії і докази себе в звичній геометричній обстановці. Мова архаїчна, але мені подобається і історія, і геометрія. З сучасної точки зору, вступні визначення давньогрецької мови занадто наївні, і деякі з ранніх пропозицій (особливо SAS) повинні бути аксіомами або доведені як наслідки невизначеного інших, але презентація дивно сучасна, враховуючи проміжні тисячоліття. Ідея настільки наполегливо уникати «Паралельного постулату» (або будь-якого з нескінченно багатьох тверджень, які логічно еквівалентні) якомога довше є досить сучасною у своїй перспективі. «Як можна довше» - це перебільшення, але мета очевидна і не відповідала протягом кількох тисячоліть до розвитку гіперболічної геометрії Боляєм (переважно сином Йоганном) та Миколою Лобачевським у 1830-х роках.

Багато інших теорем, які «відчувають себе евклідовою геометрією», також можуть бути доведені в "нейтральній" або "абсолютній" геометрії (що охоплює як евклідову, так і гіперболічну геометрію), які ми вивчимо в Главі 2, такі як «Гіпотенуза-Лег», «побудова вхідного кола трикутника» та «побудова дотичні від точки до кола» разом з багатьма іншими, які є доказовими в цьому контексті (немає Паралельного постулату) перед главою 3, де ми спеціалізуємося, використовуючи заперечення Паралельного постулату, який (у поєднанні з іншими аксіомами нейтральної геометрії) є гіперболічною геометрією.

Жодна з цих геометрій не є «реальним світом», в якому ми живемо; тобто на поверхні сфери, особливий випадок еліптичної геометрії. Навіть там багато теорем дотримуються обмежень, що цифри не будуть «занадто великими», що б це не означало. Цей контекст може бути корисним для розуміння деяких результатів (так іноді буде використовуватися тут), але не слід розглядати як частину заперечення Паралельного постулату, оскільки, враховуючи інші аксіоми, виникають великі відмінності. На сфері «лінія» - це «велике коло»; тобто площина якого містить центр сфери. Використовуючи земну кулю як конкретну модель, всі поздовжні лінії є лініями в геометрії, але всі вони проходять через Північний і Південний полюси, тому навіть найбільш фундаментальні, «дві точки визначають лінію», потребує певного перегляду. Як інший приклад, розглянемо три точки поспіль на екваторі (лінія в цій геометрії, інші кола широти НЕ є лініями)) A, B і C. Тепер подумайте про «ковзання»\(C\) по всьому світу, щоб бути вишикуватися як\(C, A\), і B. Спочатку B «відчував, що» це було між A і C. тепер, це A, який має таке почуття щодо\(C\) і B резолюції? Поняття «міжності», яке присутнє і важливе в нейтральній геометрії - не існує в сферичній геометрії, принаймні, не таким же необмеженим способом. Тим не менш, мислення про сферичні трикутники та інші геометричні фігури може бути корисним для розуміння дійсності та/або обмежень теорем в інших параметрах геометрії. Коли вони не відповідають дійсності сферичної геометрії, це допомагає нам більш ретельно продумати наші докази тверджень. Часто причини явних доказів невдачі менш очевидні. Один просвітницький приклад: На сфері будь-який трикутник - такий як трикутник (в ідеалі і ідеально), намальований на залитому бетонній підлозі - має суму кута строго більше\(180^{\circ} !\)

З сучасної точки зору, вступні визначення давньогрецької мови занадто наївні, і деякі з ранніх пропозицій (особливо SAS) повинні бути аксіомами або доведені як наслідки невизначеного інших, але, загалом кажучи, презентація дивно сучасна з огляду на проміжні тисячоліття. Це зміст глави 1. Після розгляду деяких загальних додаткових теорем нейтральної геометрії в главі 2, ми почнемо обговорювати деякі властивості та доводити деякі теореми, унікальні для гіперболічної геометрії в главі 3. Для більшості обізнаних людей при першому введенні вони можуть здатися досить незрозумілими, навіть неправильними. Компетентність з формальною дедуктивною логікою, тобто доказом, зробить результати неминучими (з цієї відправної точки), але вони все ще можуть мати повітря переконання. Гіперболічна геометрія набагато більше, ніж ми будемо вивчати, але, знову ж таки, у нас є лише один термін, так що це буде лише короткий вступ з основною метою є розвиток ретельного читання та докази в математиці, а не володіння змістом або гіперболічної геометрії або передової евклідової геометрії, обидві важливі теми, гідні вивчення на даному етапі вашої кар'єри.

Обґрунтованість аксіом гіперболічної геометрії встановлюється шляхом перевірки «відносної узгодженості» з евклідовою геометрією, тобто шляхом встановлення моделі для цієї «нової» геометрії цілком у межах евклідової геометрії. Тобто, якщо щось коли-небудь буде доведено непослідовним у цій новій геометрії, це означатиме невідповідність у геометрії, яку ми всі вважаємо, евклідової геометрії. Насправді це одна довга складна теорема евклідової геометрії з великою кількістю деталей. З цією метою вибирається підмножина евклідової площини, в межах якої переосмислюють конструкції «нормальної» геометрії; тобто дають нові специфікації того, що називати точками, лініями, мірою відрізків лінії тощо, та взаємозв'язками між ними. В рамках цієї установки кожна аксіома (постулат) гіперболічної геометрії повинна бути доведена як теорема Евкліда; тобто, використовуючи будь-яку з аксіом і теорем евклідової геометрії, необхідні. Тобто ми вільні використовувати умовні точки, лінії тощо всієї евклідової площини та всіх теорем серед них, щоб довести кожну з аксіом гіперболічної геометрії як теореми в моделі. Багато необхідних результатів з евклідової геометрії не розглядаються у вступних курсах евклідової геометрії, тому нам потрібно буде ввести та вивчити деякі властивості евклідової геометрії, які є «добре відомими», але більш просунутими, ніж геометрія середньої школи.

Слід зазначити, що ця теорема про узгодженість є тривіальним наслідком комплексного аналізу (Лінійні дробові перетворення та конформне відображення). Однак більшість студентів математики не мають такого рівня математичної складності на цьому етапі (і багато хто ніколи не буде!). Більше того, багато чого можна отримати від огляду елементарної евклідової геометрії, а також нового матеріалу, вивченого в процесі (особливо інверсії по колу). Ще гірше, іноді ідеї в комплексному аналізі не доводяться, а відносяться до знань учня евклідової геометрії. У цьому немає нічого поганого, крім того, що його не можна використовувати обома способами; кругові міркування - це ні-ні в математиці!

Після того, як стверджував, що напівформальна дедуктивна логіка була найважливішим даром стародавніх греків сучасній людській думці, і що геометрія є ефективним і найпоширенішим (дещо) формальним введенням до цього процесу, може стати несподіванкою, що формального аксіоматичного розвитку не буде зроблено в цьому курсі. Це ще гірше, ніж це; колекція аксіом, які ми будемо використовувати, ніколи навіть не буде викладена! Проблема полягає в тому, що в справді формальному розвитку, навіть основна теорія множин та реальний аналіз, повинні бути аксіоматично розроблені. Навіть приймаючи наївну теорію множин та властивості дійсних чисел як належне і зосереджуючись лише на геометрії, все одно вимагатиме рівня формальності, який би перешкоджав отриманню багато іншого за весь курс. Ми візьмемо протилежну крайність і лише констатуємо найбільш критичну з аксіом, але скільки формальності буде очікувати, важко точно оцінити. Сподіваюся, у вас швидко виробиться «відчуття» до нього. Насправді, вам, можливо, доведеться «відучити» деякі фальшиві формальності; наприклад, на цьому рівні і за його межами стандартно ігнорувати твердження, які логічно необхідні, але настільки очевидні, що їх включення буде педантичним. Знання того, що є «очевидним», а що вимагає тверджень перевірки, може бути складним, звичайно; серед інших проблем це залежить від витонченості як письменника, так і цільової аудиторії.

Терміни аксіома і постулат приймають бути взаємозамінними і означають твердження, які приймаються без доказів. Однією з «помилок» греків було припустити, що деякі твердження настільки очевидно універсально вірні, що завжди бути правдою без доказів і, отже, безпечною відправною точкою. Більш сучасна перспектива полягає в тому, щоб повністю залишити концепцію «універсальної істини» поза змішуванням. Якщо ми знаходимося в обстановці, де твердження є істинними - так звана «модель» геометрії - що ще має бути правдою, оскільки це вже було доведено? Якщо ні, це теж добре; ми просто в деяких інших умовах, можливо, однаково корисно, можливо, навіть більше. Ті самі твердження можуть бути правдивими, а можуть і не бути правдивими, але, якщо вони є, вони вимагають нових доказів.

Аксіома 1 - (Для решти курсу!) - Дві точки визначають лінію.

Якщо це вам не здається знайомим, ви, ймовірно, в неправильному курсі! Однак насправді знати, що це означає, сильно відрізняється. Що таке «бали»? Що таке «лінії»? Що означає «визначити»?

Можливо, дивно, що (крім будь-якої моделі) точка і лінія будуть прийняті як невизначені терміни, обмежені певними аксіомами (які також ніколи офіційно не вказані). Більш дивно, мабуть, те, що в будь-якій аксіоматичній системі повинні бути невизначені терміни або структура за своєю суттю кругова. На встановленому рівні «набір» і «елемент множини» не визначені. Чи не набір означає «колекцію» або щось таке? Ну а що означає «колекція»? Тобто зупинятися ніде, так що за тисячоліття формальні логіки навчилися не намагатися. Але, якими б вони не були, вони поводяться певним чином; тобто відповідно до тверджень, які називаються аксіомами. Для теорії множин і дійсних або комплексних чисел ми навіть не почнемо намагатися сказати, що вони аксіоматично; ми просто будемо використовувати їх за бажанням (разом з більшістю математиків майже весь час).

Перш ніж ми почнемо, є деякі властивості набору аксіом, які потрібно зрозуміти.

Найбільш фундаментальним є те, що вони повинні бути послідовними; тобто, що вони не мають властивих суперечностей. Іншими словами, дуже важливо бути впевненим, що вони не можуть призвести до тверджень, які можуть бути як доведені, так і спростовані; тобто виявилися як істинними, так і хибними всередині системи. Таке твердження зруйнувало б всю конструкцію.

Доведення того, що ніяких подібних притаманних протиріч не може виникнути, є проблемою саме по собі. Насправді, в дуже реальному сенсі, це нездійсненне завдання! Цілком всередині самої системи неможливо довести, що аксіоми є послідовними. Стандартним доказом узгодженості набору аксіом є створення «моделі»; конкретна реалізація ситуації (і навіть «бетон» знаходиться в очах глядача!) в якому всі аксіоми можуть бути доведені як теореми. Наприклад, якщо ми маємо достатню віру в звичайну декартову (x, y) площину, вона дає приклад моделі евклідової геометрії, і, з цим припущенням, аксіоми евклідової геометрії повинні бути узгодженими. Для абстрактних систем найбільше, на що ми можемо логічно сподіватися, - це відносна послідовність; якщо ми приймаємо одну систему послідовною, використовуйте це, щоб довести, що інша також повинна бути.

Менш критичним, але бажаним властивістю є те, що аксіоми бути незалежними. Це означає, що довести жоден з них, використовуючи тільки інші, неможливо. Якщо не мати цю властивість, не знищить систему, але вона, безумовно, є кращою. Чим менше і фундаментальніше аксіом, тим «чистіше» структура. Ми могли зіткнутися з теоремою Піфагора в 6-му або 7-му класі, але вона не була представлена як аксіома Піфагора тільки тому, що ми ще не могли зрозуміти докази. Ідея полягала в тому, що це було прийнято, щоб бути правдою без наших доказів, але не без чиїсь доказів. Аксіоми не просто «витягнуті з повітря»; мудрий вибір їх - дуже складний процес, і ми не почнемо намагатися. Ми навіть не намагатимемося перерахувати їх, але деякі відомі варіанти легко доступні і будуть згадані нижче.

Третя властивість, яку може мати система, полягає в тому, що аксіоми є категоричними. Це не завжди бажана властивість, оскільки це означає, що ми маємо справу в дуже спеціалізованих обставин, коли в математиці ми часто хочемо вивчити властивості, які застосовуються до багатьох за своєю суттю різних ситуацій. Наприклад, «група» в математиці - це спеціалізований термін, який застосовується до безлічі різних структур, які відповідають груповим аксіомам, але, якщо додати до них, що група має рівно сім елементів, набір аксіом стає категоричним. У цілком реальному сенсі така група всього одна. Тобто, якщо набір аксіом категоричний, все «моделі» обстановки можна розглядати як зовні різні форми точно одного і того ж. На жаргоні всі моделі «ізоморфні». З плюсового боку, якщо набір аксіом, як відомо, є категоричним, теорема, доведена в контексті однієї моделі, також повинна бути дійсною у всіх інших моделям. Як приклад, якщо ви знайомі з «аналітичним» доказом порівняно з «синтетичним» доказом у евклідовій геометрії, знання того, що аксіоми категоричні, запевняє нас, що достатньо будь-якого доказу. Теорема в будь-якій моделі - це теорема в геометрії. (Див. Розділ 4.)

Що являє собою модель настройки? Давайте збережемо його з точки зору геометрії площини. Геометрія - це абстрактний набір елементів, які називаються «точками», певні абстрактні підмножини яких називаються «лініями» та, можливо, іншими спеціальними множинами, припускаючи, що вони задовольняють певним обмежуючим властивостям, які називаються аксіомами. Модель для цієї геометрії - це, в деякому сенсі, практично протилежне. Це дуже конкретна множина, елементи якої називаються точками, конкретні підмножини цих точок, звані лініями і колами і т.д., а всі аксіоми геометрії (тобто твердження, прийняті без доказів в геометрії) доведені як теореми в моделі. У цей момент всі теореми геометрії також стають теоремами в моделі, тобто вони вже доведені.

Ось два відомих набори аксіом, які легко доступні:

• Аксіоми Гільберта для евклідової геометрії:

• Аксіоми Біркгофа для евклідової геометрії:

Примітка: З цих формальних наборів аксіом (які ми не будемо використовувати формально) лише Birkhoff (1959) включає те, що відомо як Постулат Правителя та Постулат транспортира. Однак Гільберт (1899 як переглянутий у 1902 році) мають на увазі результати, що відповідають їм [Google: DesArgues/Pappus/Field та/або див. Блюменталь,\(A\) Сучасний погляд на геометрію, V.H. Freeman & Co, 1961] і були переглянуті, щоб включити їх Сондерсом Маклейн в 1923 році. Вони не використовувалися греками (хоча деякі з тих самих ідей були присутні, але виражені в терміні порівняння відрізків ліній (для довжини), багатокутників (для площі) та кутів (для вимірювання кута). Ми включимо їх, але використовуємо їх дещо неофіційно наступним чином:

Постулат лінійки: Існує відповідність 1-1 між точками на даній лінії та дійсними числами, які поводяться «приємними способами»; тобто, враховуючи відстань та напрямок, існує унікальна точка, визначена і навпаки. Тобто, як тільки лінія «координатизована», кожна точка відповідає унікальному дійсному числу, і ця асоціація відрізків рядків узгоджується з арифметикою дійсних чисел. Для відрізків лінії ця відстань між її кінцевими точками називається мірою відрізка лінії, але слово «міра» вводить в оману; вимірювання не беруть участь, оскільки всі вимірювання є приблизними, і вони вважаються нескінченно точними.

Постулат транспортира: Існує відповідність 1-1 між кутами, що починаються з даного променя, і дійсними числами замкнутого інтервалу\([0,180]\) (або або\([-90,90]\) або\([0, \pi]\)\([-\pi / 2, \pi / 2]\) або будь-яких інших таких, включаючи ті, які можуть бути розумними. але майже ніколи не використовуються такі як\([0,100]\)) такі, що, враховуючи розмір кута і напрямок, існує унікальний промінь визначається і навпаки. Після того, як півколо «координується», кожен промінь відповідає унікальному дійсному числу інтервалу і, знову ж таки, ця асоціація узгоджується з арифметикою дійсних чисел. Це асоційоване число називається мірою кута, але, знову ж таки, вимірювання не беруть участь. Нескінченна точність завжди передбачається, якщо не вказано інше (майже ніколи).

Останній раз ці ідеї (особливо їх назви) можуть бути трохи оманливими; фактичних вимірювань не відбувається, оскільки це було б за своєю суттю приблизним. Це лише теоретичні абстракції. Вважається, що все буде нескінченно точним, що ніколи не можливо в ситуаціях вимірювання. Більше того, якщо не вказано інше, від вас очікуватимуть нескінченної точності, тому калькулятори не допоможуть, крім як захисне ковдру. За винятком основних іспитів, вони не будуть заборонені, але відповіді, як очікується, будуть точними; наприклад,\(\pi\)\(3.14\) ні ні ні\(0.2857\), і т.д. десяткові відповіді прийнятні тільки в\(3.14159,2 / 7\) тому випадку, якщо вони точні - десяткові наближення не отримають повний кредит. Спрощених звичайних дробів буде достатньо для курсу і, по суті, є кращими, коли це доречно. Калькулятори, стільникові телефони тощо будуть заборонені з середньострокової та остаточної, оскільки вони стали занадто «розумними»; тобто вони можуть записувати інформацію та надавати вам доступ до інформації, яка повинна бути у вашій голові, щоб мати можливість ефективно мислити.

Як ми можемо діяти аксіоматично, ніколи не заявляючи про більшість аксіом явно? Сподіваємось, ви отримаєте ідею, коли ми прогресуємо. Однією з важливих ідей, про яку ми будемо «неохайними», є «міжність» точок на лінії, але вона повинна «бути там», незалежно від того, турбуємося ми про це чи ні. Інший - міркування наступності. Скажімо, наприклад, відрізок лінії визначається точкою всередині кола і іншою за її межами. Має бути очевидним - і ми сприймемо це як належне - що є точка перетину цього відрізка і кола. Потрібні формальні аксіоми, але вони будуть проігноровані.

Ця ж ідея стосується і визначень. Вони абсолютно критичні, і все ж багато хто з них не будуть надані в курсі, принаймні явно. Якщо є якісь сумніви щодо того, що істинно «за визначенням» щодо якогось названого об'єкта, запитайте, і уважно відзначте це у власному особистому глосарії. Заявлення про те, що властивість якоїсь геометричної структури є істинною за визначенням, коли вона не є частиною визначення, але була доведена натомість, є серйозною помилкою, тому будьте обережні. Якщо є будь-яка неоднозначність, включіть також назву слова, на яке посилається; наприклад, «за визначенням прямокутника» замість просто «за визначенням». [Що таке визначення прямокутника? Чотирикутник з усіма кутами прямими кутами. Нічого більше. Все інше повинно бути доведено.]

Скорочення - це ще одне місце, де слід здійснювати догляд в тому сенсі, що їх «повномасштабні» форми потрібно чітко пам'ятати. Тобто абревіатура не повинна використовуватися, якщо і письменник, і читач не зможуть розширити її еквівалентно і без зусиль. Хорошим прикладом в геометрії є SAS. Якщо у вас немає слабких англійських або математичних навичок, ви можете прочитати його відразу як «Side-Angle-Side». Це не те, що мається на увазі під «розширенням його»; це лише абревіатура. SAS - це твердження; тобто це повне (у нашому випадку англійське) речення, яке має істинне значення. Більш того, це універсальне твердження; в даному випадку - твердження про всі трикутники, які відповідають умовам SAS. У геометрії - і в математичних установках загалом прийнято припускати універсальність (тобто «для кожного...») тверджень, які «звучать як це». Загалом, абревіатура не повинна використовуватися, якщо ви не можете розширити її однозначно на вимогу, а не як якийсь дослівний, зворотний відповідь, але точно такий же математичний зміст з якомога меншою кількістю математичних символів та/або цифр, наскільки це можливо і узгоджується з розширенням, що будь-який інший обізнаний практикуючий дав би це. Окрім того, що SAS є універсальним твердженням, SAS є прикладом умовного твердження або імплікації; тобто, це твердження «якщо..., то...», як обговорювалося раніше, а SAS є лише абревіатурою своєї гіпотези, а не її висновком, а тим більше весь підтекст.

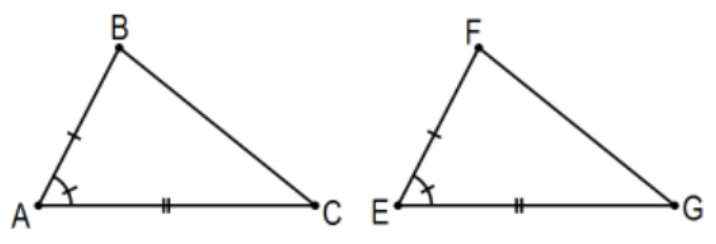
SAS: Якщо два трикутники мають дві пари сторін конгруентні і кути, включені цими парами сторін, конгруентні, то трикутники конгруентні.

Це правда? Принаймні має сенс запитати, так що це заява! Пояснюючи його значення тому, хто не знає, що це означає, було б зрозуміліше, якби підтримала хороша цифра з належним чином зазначеними умовами. Це, однак, повинно бути тривіальністю для особи, яка використовує твердження, та для особи, яка її читає чи чує; інакше абревіатура взагалі не повинна використовуватися. Їхні зображення мали б трикутники різної форми (але жоден з них не повинен бути спеціалізованим; тобто не прямі трикутники, не рівнобедрений тощо) і, ймовірно, будуть позначені по-різному, але вони б передавали точно таку ж ідею. Одна річ, яка, ймовірно, була б однаковою - це використання «знаків конгруентності», стандартних індикаторів «галочки», що відрізки лінії або кути є конгруентними та спеціальною позначкою для прямих кутів. ВИКОРИСТОВУЙТЕ ЇХ! На жаль, моє найпотужніше графічне програмне забезпечення, Попелюшка, не включає їх, тому будуть випадки, коли вам потрібно буде додати їх у себе. Це повинно бути легко зробити з контексту. Ще один момент, ви можете звикнути бачити такі висловлювання, представлені штучно, такі як:

Дано:\(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), і\(\angle \mathrm{A} \cong \angle \mathrm{E}\) (або\(\angle \mathrm{BAC} \cong \angle \mathrm{FEG}\))

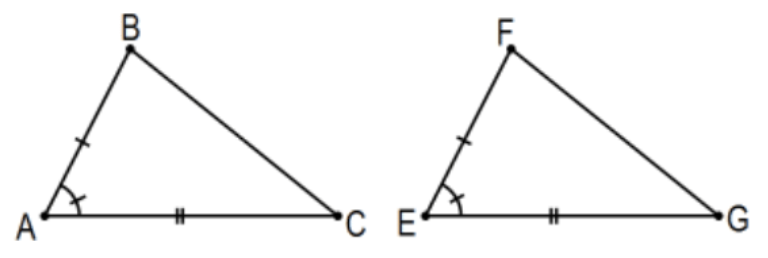
Висновок:\(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\)

Примітка: Інший (і гірше!) обмеження мого програмного забезпечення полягає в тому, що важко і спотворює міжрядковий інтервал, щоб поставити математично відповідні смуги над відрізками ліній\((\overline{\mathrm{AB}})\), стрілки над променями\((\overline{\mathrm{AB}}\) або\(\overleftarrow{\mathrm{BA}})\), двоголові стрілки над лініями\((\overleftrightarrow{\mathrm{AB}})\) та дуги над дугами \((\overparen{\mathrm{AB}})\)при позначенні двома точками, як правило, великими англійськими літерами. ВИКОРИСТОВУЙТЕ ЇХ у своїй роботі послідовно і правильно. Також будьте уважні до «відповідного наказу». Наприклад, у вищесказаному ми не мали б підстав підозрювати\(\triangle \mathrm{ABC} \cong \triangle \mathrm{EFG}\) це,\(\triangle \mathrm{ABC} \cong \triangle \mathrm{FEG}\) але еквівалентно оригіналу. Примітка: Як уже згадувалося вище, зараз це (універсальне) умовне твердження або імплікація (тобто якщо... то...), але часто вони не так викладені в математиці. Ви повинні бути в змозі легко зробити переклад в еквівалентне твердження, яке має таку форму і визнати універсальність, коли це мається на увазі.

Штучна особливість, до якої ви можете звикнути, - це так зване «T-proof»; твердження ретельно узгоджені з відповідними причинами, чому твердження вірні в контексті доказу. Якщо ви відчуваєте себе більш комфортно з таким, не соромтеся використовувати структуру, але насправді це просто педагогічна техніка, щоб переконати початківців студентів математики, що якщо заяву зроблено без підтверджуючої причини (це можна зрозуміти, але не чітко вказати), це не є доказом. Правда? Можливо, але не доведено.

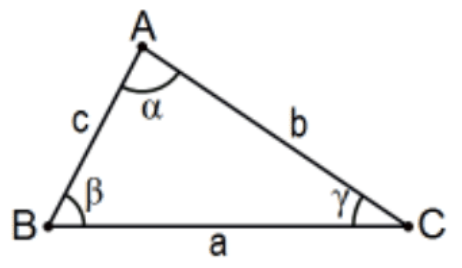
Ще одна деталь, яка буде використана, і вам також рекомендується використовувати, - це стандартні позначення, деякі з яких є обов'язковими, а деякі з яких є лише кращими. (Ця перевага може бути стандартною за межами США). Точки будуть позначені великими літерами англійського регістру, а вершини багатокутника повинні бути вказані в послідовному порядку (за годинниковою стрілкою або проти годинникової стрілки).

Так само відповідні вершини відповідних багатокутників (зазвичай конгруентних або подібних, але не обов'язково) повинні бути перераховані у відповідному порядку. Змінна, записана всередині кута, вказує на міру кута - тобто його розмір кута - не назва самого кута, тому НЕ вказуйте кут, використовуючи його розмір замість назви, кілька кутів можуть мати однаковий розмір, але, очевидно, різні назви.

Зручною умовністю, але далеко не стандартною, є використання відповідної малої грецької літери для міри кута з однойменним англійським ім'ям. Тобто часто\(\mathrm{m}(\angle \mathrm{A})\) буде вказуватися по\(\beta\),\(\alpha, \mathrm{m}(\angle \mathrm{B})\)\(\mathrm{m}(\angle \mathrm{C})\) по\(\gamma\) (тому що він наступний в грецькому алфавіті) і т.д., і використовувати малі англійські літери для позначення міри сторони і часто буде однаковим буква (але мала) протилежної вершини. Sketchpad Geometer автоматично «заповнює» індикатори вимірювання кута. НЕ робіть цього у своїй роботі; це не стандартне використання. Інший коментар щодо використання, геометричні об'єкти, такі як кути, відрізки ліній та багатокутники, які (неофіційно кажучи) однакового розміру та форми, вважаються конгруентними, на відміну від «рівних»\((\alpha, \beta, \mathrm{a}, \mathrm{b}\), але вимірювань тощо) є дійсними числами, тому, якщо вони однакові, відповідні слово «дорівнює». Ця турбота зі словами (не спільними всіма геометрами) походить від їх основної природи як наборів точок. Множини рівні тоді і лише тоді, коли вони мають однакові елементи, тому узгодженість вимагає, наприклад,\(\angle \mathrm{A}=\angle \mathrm{B}\) означатиме, що два кути (об'єднання двох променів із загальною початковою точкою) були точно такими ж двома променями, а не двома кутами однакового розміру, що, ймовірно, було наміром ; замість цього висловити це символічно, як\(\angle A \cong \angle B\) і прочитати, що як «кут\(A\) конгруентний до кута\(B\)».

Щоб отримати уявлення про те, як працює цей формальний/неформальний доказ, нижче наведені пункти з загальної першої вікторини разом із запропонованими рішеннями (які дуже схожі на пункти Набору проблем 1, далі PS 1). Інструкція почалася просто з: «Всі елементи відносяться до даного рівнобедрений трикутник»\(\triangle \mathrm{ABC}\). Мається на увазі, звичайно, те, що означає рівнобедрений, навіть сам трикутник. Існує багато таких «знайомих» термінів, які використовуються тут і протягом усього курсу, такі терміни, як «перпендикулярно», «промінь», «бісектриса кута», ASA та SSS. Сподіваємося, ці ідеї не нові, хоча і будуть переглянуті. Той, який ми будемо використовувати, який є загальним, але не універсальним, - це «cpctc», «відповідні частини конгруентних трикутників конгруентні». Аналогічно, можна сказати «за конгруентністю трикутників» (або конгруентних геометричних фігур загалом), але cpctc настільки зручний і настільки широко використовується, що я заохочую його використання. Знову ж таки, складіть собі точний глосарій термінів, щодо яких у вас є сумніви (після того, як запитаєте, чи є щось, про що ви не впевнені).

Всі елементи відносяться до заданого рівнобедреного трикутника\(\triangle \mathrm{ABC}\) з базовими кутами в\(B\) і\(\mathrm{C}\).

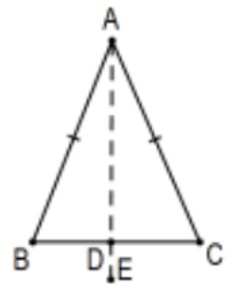
1. Вкажіть в ескізі всю надану інформацію стандартним способом. Не менш важливо вказувати нічого, крім наданої інформації.

Рішення: Додайте відповідні позначки конгруентності, «галочки» до сегментів\(A B\) та\(A C\).

2. Припустимо, що точка\(D\) є точкою, визначеною бісектрисою\(\angle A\). Доведіть це\(\angle B \cong \angle C\).

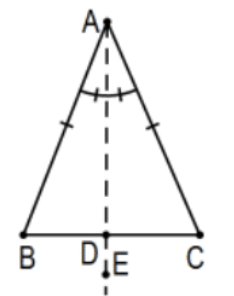
Розв'язок:\(\mathrm{AB} \cong \mathrm{AC}\) за визначенням рівнобедрених (або «заданих») та\(\angle \mathrm{BAD} \cong \angle \mathrm{CAD}\) за визначенням бісектриси кута (або «заданого»). Тому\(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) за допомогою SAS та\(\angle \mathrm{B} \cong \angle \mathrm{C}\) cpctc. [Примітка: Що сталося з\(\mathrm{AD} \cong \mathrm{AD}\) необхідним для\(\mathrm{SAS}\)? Формально це рефлексивне властивість конгруентності, але не турбуйтеся. Хіба це не очевидно так?!]

3. Припустімо, що точка\(\mathrm{D}\) є середньою точкою відрізка лінії\(B C\). Доведіть це\(\angle B \cong \angle C\).

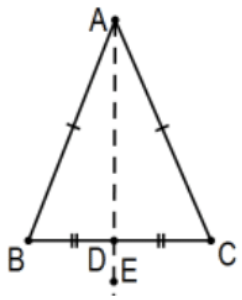
Рішення:\(\mathrm{AB} \cong \mathrm{AC}\) за\(\mathrm{BD} \cong \mathrm{CD}\) визначенням та за визначенням середньої точки (або «дано»). Тому,\(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) по\(\mathrm{SSS}\) і\(\angle \mathrm{B} \cong \angle \mathrm{C}\) по cpctc.

4. Припустимо, що лінія DE - перпендикулярна бісектриса відрізка лінії BC. Не доводьте нічого, але поясніть, чому легкий гіпотенузи-нога «доказ», що\(\angle \mathrm{B} \cong \angle \mathrm{C}\) є помилковим.

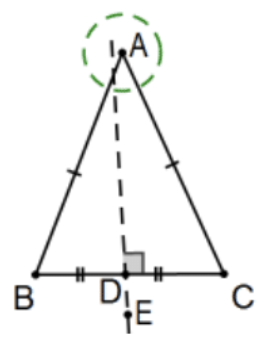
Відповідь: Для всіх, що ми знаємо на даний момент, точка А не повинна бути на лінії DE.
(Коло у вершині А показує, як можна намалювати фігуру, щоб підкреслити це.) Тобто «доказ» передбачає, що\(\mathrm{A} \in \mathrm{DE}\) без попереднього доведення цього факту.

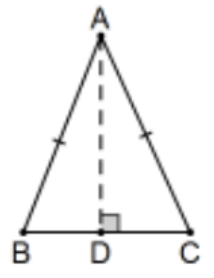
Valid Proof: Припустимо, що\(\mathrm{D}\) це підніжжя перпендикуляра від\(A\) до лінії\(B C\) (тобто немає галочок, що\(B D \cong C D)\). Тепер, по Hyp-Leg,\(\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}\) і\(\angle \mathrm{B} \cong \angle \mathrm{C}\) по cpctc.

Примітка: Проблема #4 є дуже важливою ідеєю. Після того, як сутність визначена (і перпендикулярна бісектриса відрізка лінії повністю визначає лінію) всі інші властивості про неї повинні бути доведені або ситуація «надмірно визначена»; тобто інформація приймається без доказів і може бути навіть помилковою. Це приблизно так само погано, як це потрапляє в «доказ». Насправді краще сказати «Я поняття не маю, як це довести».

5. Тільки використовуючи\(\triangle \mathrm{ABC}\) (тобто без допоміжних точок або ліній), довести\(\angle \mathrm{B} \cong \angle \mathrm{C}\).

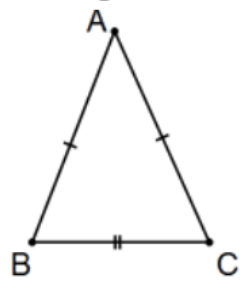
Рішення:\(\mathrm{AB} \cong \mathrm{AC}\) за визначенням і\(\mathrm{BC} \cong \mathrm{CB}\). Тому,\(\triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\) по\(\mathrm{SSS}\) і\(\angle B \cong \angle C\) по cpctc. [Тобто трикутник конгруентний собі, використовуючи іншу відповідність.] Так\(\mathrm{SAS}\) як і\(\angle \mathrm{BAC} \cong \angle \mathrm{CAB}, \triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\) по.

Примітка: Два докази #5 трохи тонші, ніж вони виглядають. Конгруентність геометричних фігур, в нашій інтерпретації, приймається у вигляді «чистої геометрії»; тобто як невизначений термін, підпорядкований деяким (хоча і невстановленим) аксіомам. Наприклад, конгруентність - це (серед іншого) відношення еквівалентності; тобто воно є рефлексивним, симетричним та перехідним. Більш явно:

i. малюнок\(\mathrm{F}\) збігається з малюнком\(\mathrm{F}\),

II. Якщо фігура\(\mathrm{F}\) конгруентна малюнку\(\mathrm{G}\), то фігура\(\mathrm{G}\) конгруентна малюнку\(\mathrm{F}\), і

iii. Якщо фігура\(\mathrm{F}\) конгруентна малюнку,\(\mathrm{G}\) а фігура\(\mathrm{G}\) конгруентна малюнку\(\mathrm{H}\), то фігура\(\mathrm{F}\) збігається з малюнком H.

На\(\mathrm{SSS}\) доказ, ми припускали\(\mathrm{BC} \cong \mathrm{CB}\) без доказів і вашого інстинкту (можливо, минуле вчення?) назвав би це істинним за рефлексивною властивістю конгруентності. Однак це не так, оскільки орієнтація зворотна. Менш «чиста» форма геометрії (наприклад, включаючи постулати лінійки та транспортира, як ми робимо) визначає конгруентність, причому не серед конкретних геометричних фігур, а всього набору точок геометрії. Формально в цьому контексті конгруентність буде визначена як відповідність один до одного всієї площини, яка зберігає відстань (непідписану міру) між будь-якими двома відповідними точками та розмір будь-яких двох відповідних кутів. Наприклад,\(\mathrm{BC} \cong \mathrm{CB}\) тому що відображення в перпендикулярній бісектрисі сегмента\(\mathrm{BC}\) - це конгруентність, яка переносить сегмент\(\mathrm{BC}\) на сегмент,\(\mathrm{CB}\) включаючи весь трикутник, про який йде мова, на себе, але з новою відповідністю. Аналогічно для доказу SAS, відображення в лінії бісектриси кута\(\angle \mathrm{BAC}\) є необхідною конгруентністю. Ще одна конгруентність, з якою ви, мабуть, знайомі, - це обертання навколо однієї точки та всіх композицій цих двох. У евклідовій геометрії переклад вектором (спрямований відрізок лінії) є іншим, іноді його називають «ковзанням» в елементарних книгах. Чи є інші? Відповідь «ні», але ми не будемо доводити цей факт у цьому курсі.

За винятком перекладів (які потребують унікальних паралелей), це також конгруенції в нейтральній (або абсолютній) геометрії; тобто без посилання на\(5^{\text {th }}\) постулат Евкліда, який дає нам евклідову геометрію, тому ці твердження вірні як в евклідовій, так і в гіперболічній геометрії, хоча ми можемо «думати» тільки евклідової геометрії (і досі не маємо уявлення про те, що може бути гіперболічна геометрія!).

Остання складність, яку часто не помічають у вступних класах геометрії, полягає в тому, що для незалежності аксіом твердження конгруентності (тобто SAS, SSS, ASA, AAS та гіпотенуза-Leg) не є «аксіомами», принаймні, не більшість з них. Хоча греки цього не усвідомлювали, одне з них (або щось еквівалентне) потрібно сприймати як аксіому, а решта - теореми, умовні твердження, які потрібно довести.

Це останнє твердження не зовсім вірно, але майже. Наприклад, в аксіомах Гільберта конгруентність сегментів і кутів описується аксіоматично, а конгруентність геометричних фігур (обмежених зв'язаними, що складаються з сегментів і кутів) потім визначаються як конгруентні, якщо існує відповідність їх точок один до одного таким чином, що всі сегменти і кути відповідають і є конгруентними. З цим обмеженням його основна аксіома не зовсім\(\mathrm{SAS}\); вона включає конгруентність відсутніх двох кутів, але опускає конгруентність відсутньої сторони та доводить повну SAS як теорему. Це настільки близько, щоб бути майже тривіальним, за винятком ідеї збереження набору аксіом на абсолютному мінімумі, необхідному. [Див. Класична книга Гільберта 1902 року, Основи геометрії, Публікація Відкритого суду, Аксіома IV, 6 та Теорема 10.]

Ми візьмемо SAS як аксіому і використаємо її для доведення інших, хоча, наприклад, замість них можна було б використовувати SSs. Хоча ССС буде викладатися самостійно, це дійсно так, «Якщо SAS, то SSS». З точки зору формальної логіки (і ігнорування зрозумілого універсального характеру ситуації); тобто, «Для кожного... «, перед попереднім і знову перед наслідком у підтексті, «Якщо\((p \Rightarrow q)\), то\((r \Rightarrow s)\) «, або повністю,"\((p \Rightarrow q) \Rightarrow(r \Rightarrow s)\)». У такій ситуації ми просто припускаємо правдивість висловлювання\(r\) і якось доводимо, що твердження теж\(s\) має бути правдою. У процесі доведення слід було б очікувати\(s\), що десь уздовж лінії, може бути кілька разів,\(p \Rightarrow q\) буде використана передбачувана істина будь-якого виникнення.

Насправді це складніше. Насправді це говорить, що «якщо всі аксіоми нейтральної геометрії, включаючи SAS і раніше доведені теореми, вірні, то SSS також вірно». У загальному плані, по всій формальній математиці, це ідея: Велика колекція «речей» використовується для доведення деякого нового умовного твердження. Жоден з цього складного попередника не згадується, лише попередник нового умовного твердження, який повинен бути доведений. Як уже згадувалося вище, ми могли б так само добре припустити,\(S S S\) як нашу аксіому і використовувати її для доведення SAS. Орієнтуючись саме на концепції конгруентності, що робить умовний оператор «Якщо SSS, то SAS» зворотним «Якщо SAS, то SSS». У такому випадку, якби ми довели твердження, ми б просто сказали: «Доведіть SAS». Для цього нам доведеться відкинути будь-які твердження, які ми вважали правдивими, оскільки вони були доведені за допомогою SAS, і якось побудувати доказ за допомогою SSS, щоб довести, що два трикутники з гіпотезою SAS насправді є конгруентними. Тобто ми починаємо з двох трикутників, які задовольняють гіпотези SAS (НЕ гіпотеза\(\mathrm{SSS}\)) і доводять, що трикутники конгруентні. Для цього налаштування могло виглядати саме так, як SAS, який ми розглядали раніше:

Дано:\(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), і\(\angle \mathrm{A} \cong \angle \mathrm{E}\) (або\(\angle \mathrm{BAC} \cong \angle \mathrm{FEG})\)

Висновок:\(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\).

Де знаходиться ССС? Кожного разу, коли і де ми маємо умови ССС для двох трикутників (не цих двох (!) , принаймні ще немає), ми маємо зробити висновок, що ці трикутники є конгруентними. Щоб довести результат, нам потрібно якось побудувати трикутники, які задовольняють умовам SSS як міст, щоб довести, що ці два також є конгруентними. Як це зробити, може бути непросто, залежно від досвіду та математичної творчості. Що б ми не робили, однак, ми повинні бути обережними, щоб не використовувати жодних теорем, які були доведені за допомогою SAS, або ми маємо чіткі, хоча і ненавмисні, кругові міркування. На цьому етапі це легко зробити, оскільки ми не довели жодних теорем, крім конгруентності базових кутів рівнобедрених трикутників, і ми запропонували SSS-доказ цього факту (який нам все одно не потрібен). Щоб побачити, як це може працювати, ми вводимо ще одне знайоме поняття:

Дозволені «інструменти» - це немаркований straightedge (реалізація аксіоми 1) та компас (реалізація «знання» кола, заданої точки для центру та відрізка лінії або його довжини для радіуса). Їх часто називають «евклідовими інструментами», але (оскільки вони є штучними реалізаціями абстрактного наслідку аксіом нейтральної геометрії), вони, як вважають, доступні протягом усього курсу, евклідової геометрії чи ні. Нові точки, лінії тощо, виявлені через них, скажуть, існують «за конструкцією».

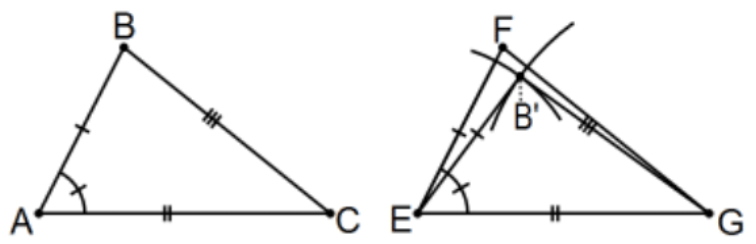
Доказ: Побудувати точку\(\mathrm{B}^{\prime}\) як відповідне перетин (E; AB), кола з центром в\(\mathrm{E}\) радіусі\(\mathrm{AB}\), і (G; CB), коло з центром в\(G\) радіусі CB. Тепер у нас є новий трикутник з\(\triangle \mathrm{EB}^{\prime} \mathrm{G} \cong \triangle \mathrm{ABC}\) SSS, оскільки у нас є три пари конгруентних сторін «за конструкцією». Тепер\(\angle B^{\prime} E G \cong \angle B A C\) тому, що відповідні частини конгруентних трикутників є конгруентними (cpctc). За гіпотезою,\(\angle B A C \cong \angle F E G\) так, транзитивністю конгруентності,\(\angle B^{\prime} E G \cong \angle F E G\). За постулатом транспортира промінь\(\mathrm{EB}^{\prime}\) і промінь\(E F\) - це точно такий же промінь. Більш того,\(\mathrm{EB}^{\prime} \cong A B\) за конструкцією і було дано, що\(\mathrm{AB} \cong \mathrm{EF}\) так, по перехідності,\(\mathrm{EB}^{\prime} \cong \mathrm{EF}\) так, за Постулатом Правителя,\(F\) і\(\mathrm{B}^{\prime}\) є точно такою ж точкою\(\left(F=B^{\prime}\right)\). Тому оригінальні трикутники є конгруентними, тому що ми вже знали, що вони конгруентні, у нас просто є інша назва однієї з точок. КАД.

Докладніше про цю проблему див. Вип. 22 наприкінці набору проблем 1 (далі вказано PS 1, #22).