5.3: Застосування тригонометрії

Last updated
Save as PDF

Page ID: 58793

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Тригонометрія має безліч застосувань в науці та техніці. У цьому розділі ми представимо лише кілька прикладів з геодезії та навігації.

Кут, зроблений лінією зору спостерігача на землі до точки вище горизонталі, називається кутом піднесення. На$\PageIndex{1}$ малюнку$\angle BAC$ - це кут піднесення.

Приклад$\PageIndex{1}$

У точці 50 футів від дерева кут піднесення вершини дерева$43^{\circ}$. Знайдіть висоту дерева до найближчої десятої частини фута.

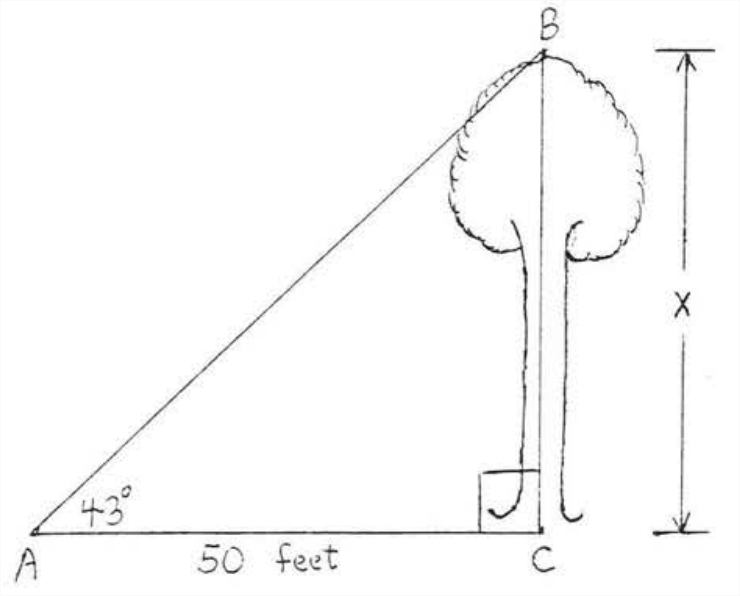
$clipboard_eb172ae95cdf1e7bc1541573428478171.png$

Рішення

Нехай$x=$ висота дерева.

$\begin{array} {rcl} {\tan 43^{\circ}} & = & {\dfrac{x}{50}} \\ {.9325} & = & {\dfrac{x}{50}} \\ {(50)(.9325)} & = & {\dfrac{x}{50}(50)} \\ {46.6250} & = & {x} \\ {46.6} & = & {x} \end{array}$

Відповідь:$x = 46.6$ ноги.

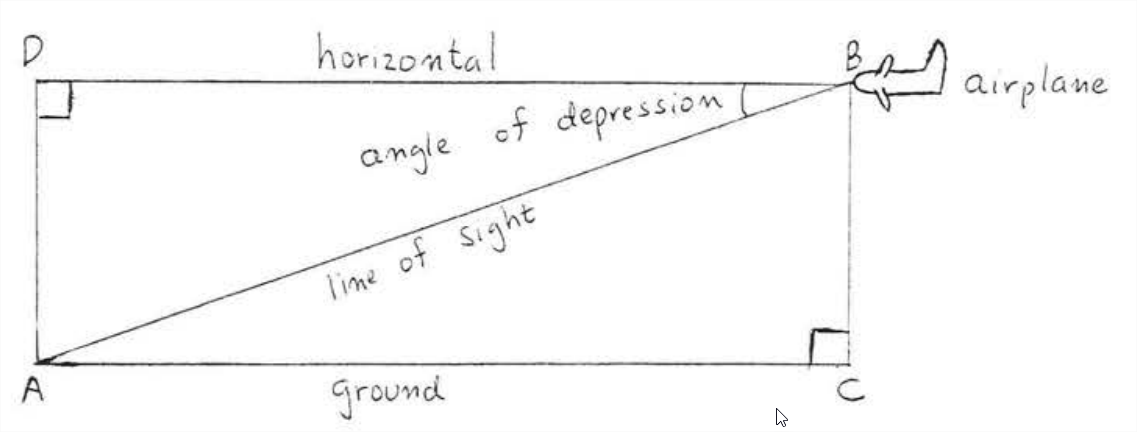
Кут, зроблений лінією зору спостерігача вище до точки на землі, називається кутом западини. На$\PageIndex{2}$ малюнку$\angle ABD$ - це кут заглиблення.

Приклад$\PageIndex{2}$

Від літака 5000 футів над землею кут депресії аеропорту$5^{\circ}$. Як далеко знаходиться аеропорт до найближчої сотні футів?

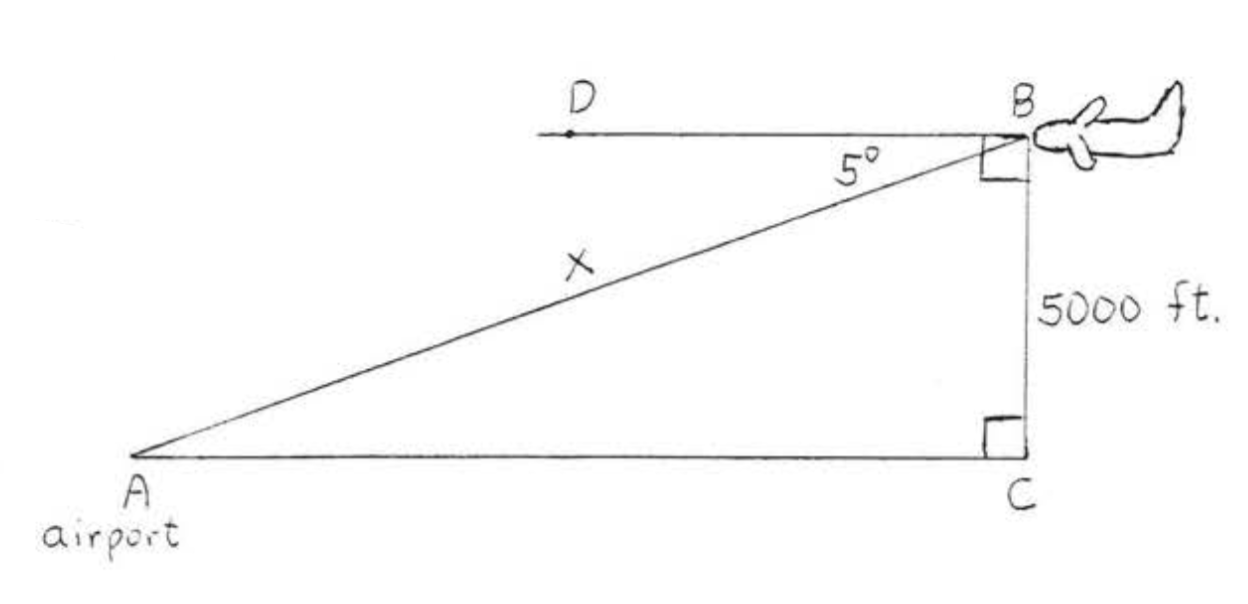
$2020-11-24 1.05.54.PNG$

Рішення

Нехай$x =$ відстань до аеропорту. $\angle ABC = 85^{\circ}$.

$\begin{array} {rcl} {\cos 85^{\circ}} & = & {\dfrac{5000}{x}} \\ {.0872} & = & {\dfrac{5000}{x}} \\ {.0872x} & = & {5000} \\ {x} & = & {\dfrac{5000}{.0872} = 57,300} \end{array}$

Відповідь: 57,300 футів

Приклад$\PageIndex{3}$

Дорога піднімається 30 футів на горизонтальній відстані 300 футів, знайти до найближчого ступеня кут дороги робить з горизонтальним.

$2020-11-24 1.09.19.пнг$

Рішення

$\begin{array} {rcl} {\tan A} & = & {\dfrac{30}{300}} \\ {\tan A} & = & {.1000} \\ {\angle A} & = & {6^{\circ}} \end{array}$

Відповідь:$6^{\circ}$.

Проблеми

1. У точці 60 футів від дерева кут піднесення вершини дерева становить$40^{\circ}$. Знайдіть висоту дерева до найближчої десятої частини фута.

2. У точці 100 футів від висотної будівлі кут піднесення верхньої частини будівлі$65^{\circ}$. Знайдіть висоту будівлі до найближчої ноги.

3. Від вертольота 1000 футів над землею кут западини helinort становить$10^{\circ}$. Як далеко знаходиться вертолітний майданчик до найближчої ноги?

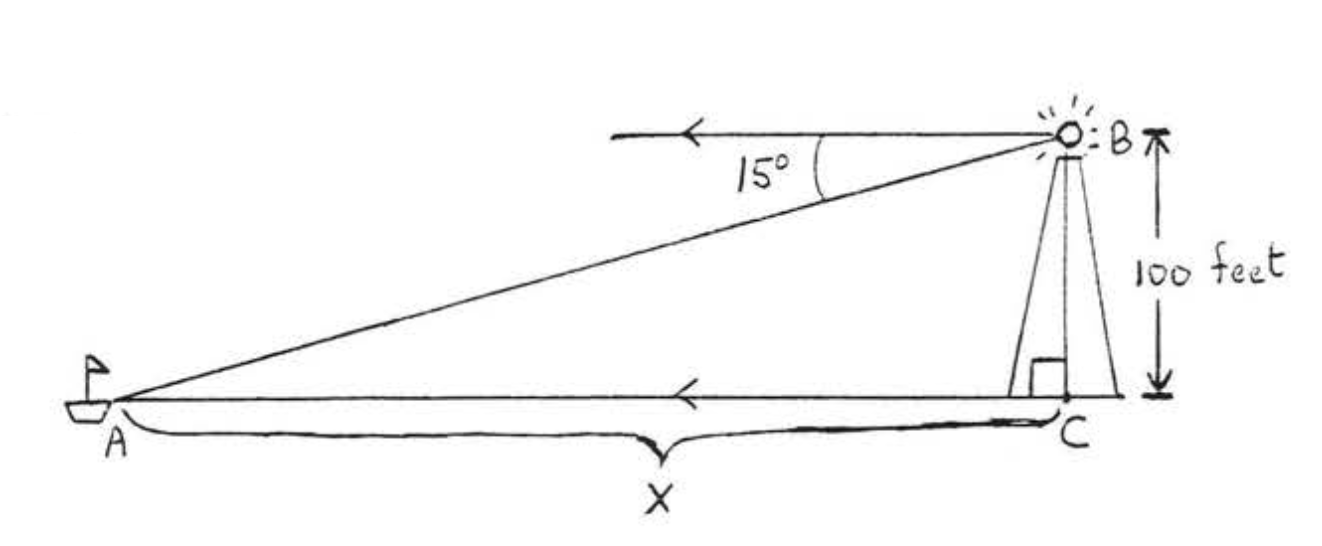
4. З вершини 100-футового маяка кут западини човна становить$15^{\circ}$. Як далеко човен від дна маяка (найближча нога)?

$Знімок екрана 2020-11-24 в 1.14.51 PM.png$

5. Дорога піднімається на 10 футів на горизонтальній відстані 400 футів. Знайдіть до найближчого градуса кут, який дорога робить з горизонталлю.

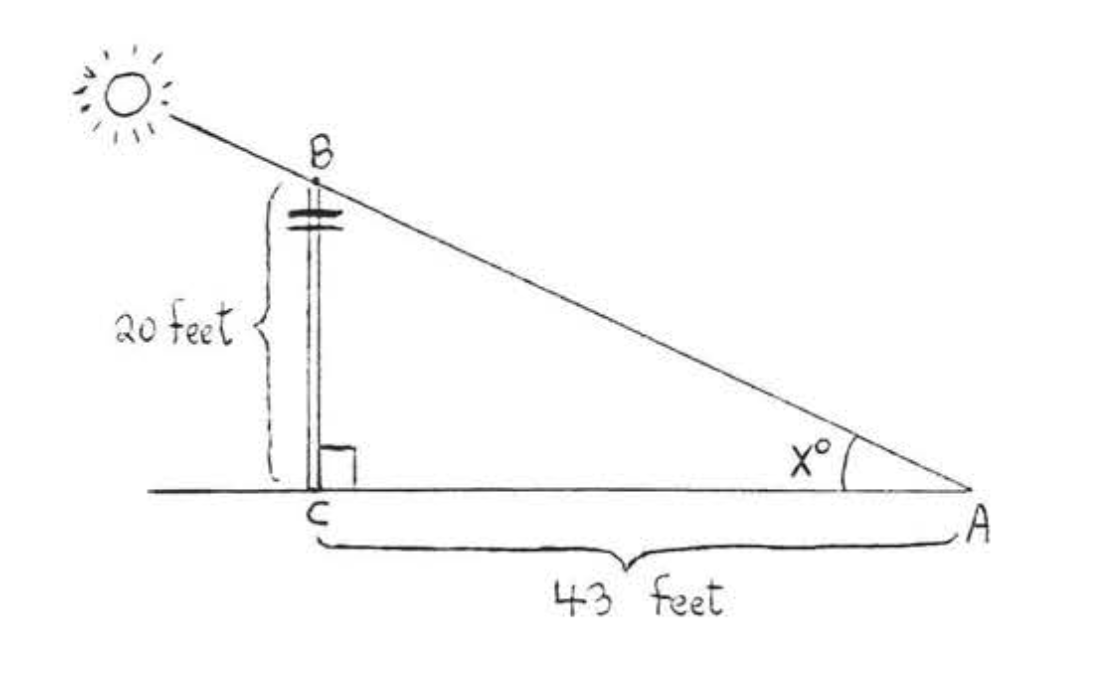
6. Якщо 20-футовий телефонний стовп кидає тінь 43 футів, який кут піднесення сонця?

$Знімок екрана 2020-11-24 в 1.15.17 PM.png$

7. А 20 футів сходи притулившись до стіни, робить кут$70^{\circ}$ з землею. Наскільки висока вершина сходів від землі (найближча десята частина фута)?

8. Кут піднесення вершини гори від точки 20 миль становить$6^{\circ}$. Наскільки висока гора (найближча десята частина милі)?

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Проблеми