Skip to main content
LibreTexts - Ukrayinska

14.1: Аффінні перетворення

  1. Last updated
  2. Save as PDF
  • Page ID
    59160

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Аффінна геометрія вивчає так звану структуру падінь евклідової площини. Структура випадковості бачить лише те, які точки лежать на яких лініях і нічого іншого; вона безпосередньо не бачить відстані, вимірювання кута та багато іншого.

    Біекція від евклідової площини до себе називається аффінним перетворенням, якщо воно відображає лінії на лінії; тобто зображення будь-якої лінії є лінією. Таким чином, можна сказати, що аффінна геометрія вивчає властивості евклідової площини, збережених при аффінних перетвореннях.

    Вправа\(\PageIndex{1}\)

    Показати, що аффінне перетворення евклідової площини посилає будь-яку пару паралельних ліній до пари паралельних ліній.

    Підказка

    Припустімо, що дві різні лінії\(\ell\) і\(m\) відображаються на пересічних лініях\(\ell'\) і\(m'\). Припустимо, що\(P'\) позначає їх точку перетину.

    \(P\)Дозволяти бути зворотним зображенням\(P'\). За визначенням аффінної карти, вона повинна лежати на обох\(\ell\) і\(m\); тобто\(\ell\) і\(m\) перетинаються. Звідси і результат.

    Нижче наведено спостереження, оскільки лінії визначаються лише за допомогою метрики.

    Спостереження\(\PageIndex{1}\)

    Будь-який рух евклідової площини є афінним перетворенням.

    Наступна вправа дає більш загальні приклади аффінних перетворень.

    Вправа\(\PageIndex{2}\)

    Наступні карти координатної площини до себе є афінними перетвореннями:

    (a) Карта нахилу визначена\((x,y) \mapsto (x + k \cdot y, y)\) для константи\(k\).

    (b) Масштабування, визначене\((x, y) \mapsto (a \cdot x, a \cdot y)\) для константи\(a \ne 0\).

    (c)\(x\) -масштабування та\(y\) -масштабування, визначені відповідно

    \((x, y) \mapsto (a \cdot x, y)\), і\((x, y) \mapsto (x, a \cdot y)\)

    для постійної\(a \ne 0\).

    (d) Трансформація, визначена

    \((x, y) \mapsto (a \cdot x + b \cdot y + r, c \cdot x + d \cdot y + s)\)

    для\(a, b, c, d, r, z\) таких констант, що матриця\(\begin{matrix} a & b \\ c & d \end{matrix}\) є оборотною.

    Підказка

    У кожному випадку перевірте, чи карта є біекцією, і застосуйте Вправу 7.6.3

    З фундаментальної теореми афінної геометрії (Теорема 14.3.1) випливає, що будь-яке аффінне перетворення можна записати у вигляді (d).

    Нагадаємо, що точки є колінеарними, якщо лежать на одній лінії.

    Вправа\(\PageIndex{3}\)

    Припустимо,\(P\mapsto P'\) це біекція евклідової площини, яка відображає колінеарні трійки точок на колінеарні трійки. Показати, що\(P\mapsto P'\) відображає неколінеарні трійки на неколінеарні.

    Зробіть висновок, що\(P\mapsto P'\) є афінним перетворенням.

    Підказка

    Вибираємо рядок\((AB)\).

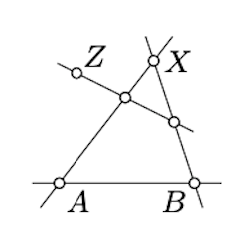
    2021-02-25 пнг

    Припустимо, що\(X' \in (A'B')\) для деяких\(X \not\in (AB)\). Оскільки\(P \mapsto P'\) карти коллайнера вказує на колінеарні\((AB), (AX)\), три лінії і\((BX)\) відображаються на\((A'B')\). Далі, будь-яка лінія, яка з'єднує пару точок на цих трьох лініях, також наноситься на карту\((A'B')\). Використовуйте його, щоб показати, що вся площина зіставлена на карту\((A'B')\). Останнє суперечить тому, що карта є біекцією.

    За припущенням, якщо\(X \in (AB)\), то\(X' \in (A'B')\). Форма над зворотним тримається, а також. Використовуйте його, щоб довести друге твердження.