11.4: Дефект

Last updated
Save as PDF

Page ID: 58973

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Дефект трикутника$\triangle ABC$ визначається як

$\text{defect} (\triangle ABC) := \pi - |\measuredangle ABC| - |\measuredangle BCA| - |\measuredangle CAB|.$

Зауважте, що теорема 11.3.1 стверджує, що дефект будь-якого трикутника в нейтральній площині повинен бути невід'ємним. Згідно з теоремою 7.4.1 будь-який трикутник в евклідовій площині має нульовий дефект.

Вправа$\PageIndex{1}$

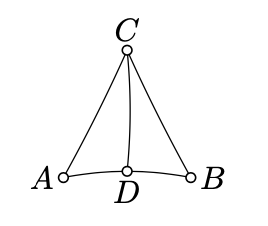
$\triangle ABC$Дозволяти невироджений трикутник в нейтральній площині. Припустимо,$D$ лежить між$A$ і$B$. Покажіть, що

$\text{defect} (\triangle ABC) = \text{defect} (\triangle ADC) + \text{defect} (\triangle DBC).$

$2021-02-23 пнг$

Підказка: Зверніть увагу, що$|\measuredangle ADC| + |\measuredangle CDB| = \pi$. Потім застосовують визначення дефекту.

Вправа$\PageIndex{2}$

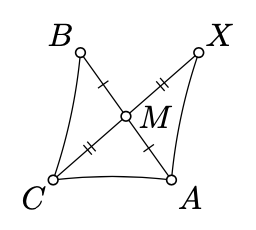
$ABC$Дозволяти невироджений трикутник в нейтральній площині. Припустимо,$X$ це відображення$C$ через середину$M$$[AB]$. Покажіть, що

$\text{defect} (\triangle ABC) = \text{defect} (\triangle AXC).$

$2021-02-23 пнг$

Підказка: Покажіть, що$\triangle AMX \cong \triangle BMC$. Застосовуйте вправу$\PageIndex{1}$ до$\triangle ABC$ і$\triangle AXC$.

Вправа$\PageIndex{3}$

Припустимо, що$ABCD$ це прямокутник в нейтральній площині;$ABCD$ тобто чотирикутник з усіма прямими кутами. Покажіть, що$AB = CD$.

Підказка

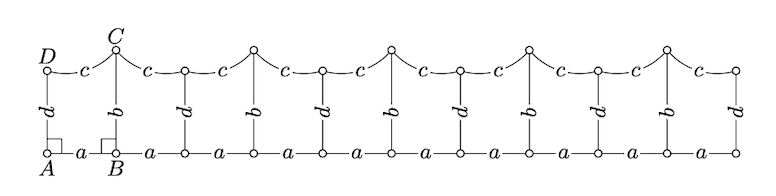
$2021-02-23 пнг$

Покажіть, що$B$ і$D$ ляжте на протилежні сторони$(AC)$. Зробіть висновок, що

$\text{defect} (\triangle ABC) + \text{defect} (\triangle CDA) = 0.$

Застосуйте теорему$\PageIndex{1}$, щоб показати, що

$\text{defect} (\triangle ABC) = \text{defect} (\triangle CDA = 0$

Використовуйте його, щоб показати, що$\meauredangle CAB = \measuredangle ACD$ і$\measuredangle ACB = \measuredangle CAD$. За АСА$\triangle ABC \cong \triangle CDA$, і, зокрема,$AB =CD$.

(Крім того, ви можете застосувати Вправу 11.3.1)

Розширені вправи$\PageIndex{4}$

Показати, що якщо нейтральна площина має прямокутник, то всі її трикутники мають нульовий дефект.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Розширені вправи\(\PageIndex{4}\)