Skip to main content
LibreTexts - Ukrayinska

11.1: Нейтральна площина

  1. Last updated
  2. Save as PDF
  • Page ID
    58963

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Видалимо Axiom V з нашої аксіоматичної системи. Таким чином ми визначаємо новий об'єкт, який називається нейтральною площиною або абсолютною площиною. (У нейтральній площині аксіома V може триматися, а може і не триматися.)

    Зрозуміло, що будь-яка теорема в нейтральній геометрії тримається в евклідовій геометрії. Іншими словами, евклідова площина є прикладом нейтральної площини. У наступному розділі ми побудуємо приклад нейтральної площини, яка не є евклідовою.

    У цій книзі Аксіома V використовувалася починаючи з глави 6. Тому всі твердження перед цим тримаються в нейтральній геометрії.

    Це робить всі обговорювані результати про півплощини, знаки кутів, умови конгруентності, перпендикулярні лінії та відображення вірними в нейтральній геометрії.

    Наведемо приклад теореми в нейтральній геометрії, яка допускає більш простий доказ в евклідовій геометрії.

    Теорема\(\PageIndex{1}\) Hypotenuse-leg congruence condition

    Припустимо, що трикутник\(ABC\) і\(A'B'C'\) мають прямі кути при\(C\) і\(C'\) відповідно,\(AB = A'B'\) і\(AC = A'C'\). Потім\(\triangle ABC \cong \triangle A'B'C'\).

    Доказ

    Евклідове доказ. За теоремою Піфагора\(BC = B'C'\). Тоді оператор випливає з умови конгруентності SSS.

    У доведенні теореми Піфагора використані властивості подібних трикутників, які в свою чергу використовували Аксіома V. Тому даний доказ не працює в нейтральній площині.

    Нейтральний доказ. Припустимо, що\(D\) позначає відображення\(A\) поперек\((BC)\) і\(D'\) позначає відображення\(A'\) поперек\((B'C')\). Зверніть увагу, що

    \(AD = 2 \cdot AC = 2 \cdot A'C' = A'D'\),\(BD = BA = B'A' = B'D'.\)

    За умовою конгруентності ССС (теорема 4.4.1) ми отримуємо це\(\triangle ABD \cong \triangle A'B'D'\).

    Заява випливає, оскільки\(C\) є серединою\([AD]\) і\(C'\) є середньою точкою\([A'D']\).

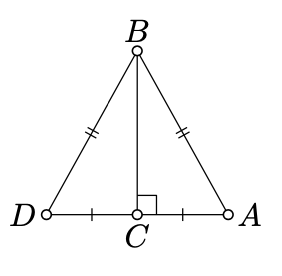
    2021-02-22 пнг

    Вправа\(\PageIndex{1}\)

    Наведіть доказ вправи 8.7.1, що працює в нейтральній площині.

    Підказка

    Припустимо, що\(D\) позначає середину\([BC]\). Припустимо,\((AD)\) це кут бісектриси в\(A\).

    \(A' \in [AD)\)Дозволяти точка відмінна від\(A\) такого, що\(AD = A'D\). Зауважте, що\(\triangle CAD \cong \triangle BA'D\). Зокрема,\(\measuredangle BAA' = \measuredangle AA'B\). Залишилося застосувати теорему 4.3.1 для\(\triangle ABA'\).

    Вправа\(\PageIndex{2}\)

    \(ABCD\)Дозволяти вписаний чотирикутник в нейтральній площині. Покажіть, що

    \(\measuredangle ABC + \measuredangle CDA \equiv \measuredangle BCD + \measuredangle DAB.\)

    Підказка

    Твердження видно\(A, B, C\), якщо, і\(D\) лежать на одному рядку. В іншому випадку припустимо, що\(O\) позначає circumcenter. Застосовуємо теорему про рівнобедрений трикутник (теорема 4.3.1) до трикутників\(AOB, BOC, COD, DOA\).

    (Зауважте, що в евклідовій площині твердження випливає з Слідство 9.3.2 та Вправа 7.4.5, але не можна використовувати ці твердження в нейтральній площині.)

    Зауважте, що не можна використовувати Слідство 9.3.2 для вирішення наведеної вище вправи, оскільки він використовує теорему 9.1.1 та теорему 9.2.1, яка, в свою чергу, використовує теорему 7.4.1.