3.4: Напівплощини

Last updated
Save as PDF

Page ID: 59048

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Пропозиція$\PageIndex{1}$

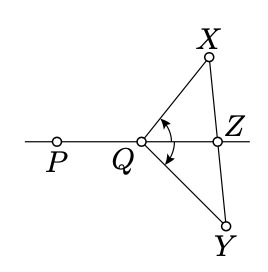
Припустимо$X, Y \not\in (PQ)$. Тоді кути$PQX$ і$PQY$ мають однаковий знак, якщо і тільки якщо$[XY]$ не перетинаються$(PQ)$.

$2021-02-02 1,56.57.PNG$

Доказ

Якщо частина випливає з леми 3.3.2.

Припустимо, що$[XY]$ перетинається$(PQ)$; припустимо, що$Z$ позначає точку перетину. Без втрати спільності можна припустити$Z \ne P$.

Зверніть увагу, що$Z$ лежить між$X$ і$Y$. Згідно з Леммою 3.1.1,$\angle PZY$ мають$\angle PZX$ і протилежні ознаки. Це доводить твердження, якщо$Z = Q$.

Якщо$Z \ne Q$, то$\angle ZQX$ і$QZX$ мають протилежні ознаки на 3,7. Так само ми отримуємо, що$\angle ZQY$ і$\angle QZY$ маємо протилежні ознаки.

Якщо$Q$ лежить між$Z$ і$P$, то по лемі 3.1.1 дві пари кутів$\angle PQX$,$\angle ZQX$ причому$\angle PQY$,$\angle ZQY$ мають протилежні знаки. Звідси випливає, що$\angle PQX$ і$\angle PQY$ мають протилежні ознаки в міру необхідності.

В іншому випадку$[QZ) = [QP)$ і тому$\angle PQX = \angle ZQX$ і$\angle PQY = \angle ZQY$. Тому знову$\angle PQX$ і$\angle PQY$ мають протилежні ознаки в міру необхідності.

Слідство$\PageIndex{1}$

Доповнення лінії$(PQ)$ в площині може бути представлено унікальним чином у вигляді об'єднання двох неспільних підмножин, званих напівплощинами, такими, що

(а) Дві точки$X, Y \not\in (PQ)$ лежать в одній півплощині тоді і тільки тоді, коли кути$PQX$ і$PQY$ мають однаковий знак.

(b) Дві точки$X, Y \not\in (PQ)$ в одній півплощині, якщо і тільки тоді, коли$[XY]$ не перетинаються$(PQ)$.

Ми говоримо, що$X$ і$Y$ лежати на одній стороні,$(PQ)$ якщо вони лежать в одній з напівплощин,$(PQ)$ і ми говоримо, що$P$ і$Q$ лежать на протилежних сторонам,$l$ якщо вони лежать в різних напівплощинами$l$.

Вправа$\PageIndex{1}$

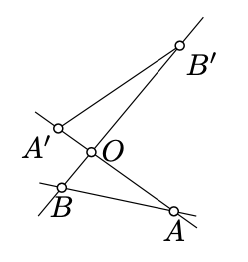
Припустимо, що кути$AOB$ і$A'OB'$ вертикальні і$B \not\in (OA)$. Показати, що лінія$(AB)$ не перетинає відрізок$[A'B']$.

$2021-02-02 пнг$

Підказка: Зверніть увагу, що$O$ і$A'$ лежать на одній стороні$(AB)$. Аналогічно$O$ і$B'$ лежать на тій же стороні$(AB)$. Звідси і результат.

Розглянемо трикутник$ABC$. Відрізки$[AB], [BC]$, і$[CA]$ називаються сторонами трикутника.

Теорема$\PageIndex{1}$ Pasch's theorem

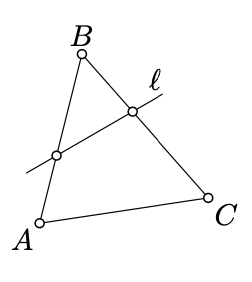
Припустімо, що лінія$l$ не проходить через будь-яку вершину трикутника. Потім вона перетинає або дві, або нульові сторони трикутника.

$2021-02-02 пнг$

Доказ

Припустимо, що лінія$l$$[AB]$ перетинає сторону трикутника$ABC$ і не проходить через$A, B,$ і$C$.

За слідством$\PageIndex{1}$, вершини$A$ і$B$ лежать на протилежні сторони від$l$.

Вершина$C$ може лежати на одній стороні з$A$ і на протилежному боці з$B$ або навпаки. За слідством$\PageIndex{1}$, в першому випадку,$l$ перетинається збоку$[BC]$ і не перетинається$[AC]$; у другому випадку$l$ перетинається сторона$[AC]$ і не перетинається$[BC]$. Звідси випливає твердження.

Вправа$\PageIndex{2}$

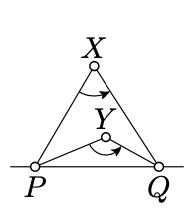
Покажіть, що дві точки$X, Y \not\in (PQ)$ лежать на одній стороні$(PQ)$ якщо і тільки якщо кути$PXQ$ і$PYQ$ мають однаковий знак.

$2021-02-02 пнг$

Підказка: Застосувати теорему 3.3.1 для,$\triangle PQX$$\triangle PQY$ а потім застосувати Слідство$\PageIndex{1}$a.

Вправа$\PageIndex{3}$

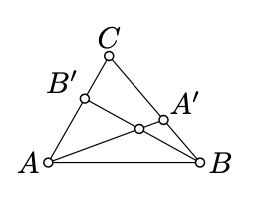
$\triangle ABC$Дозволяти бути невиродженим трикутником,$A' \in [BC]$ і$B' \in [AC]$. Покажіть, що відрізки$[AA']$ і$[BB']$ перетинаються.

$2021-02-02 пнг$

Підказка

Можна припустити, що$A' \ne B, C$ і$B' \ne A, C$; інакше твердження тривіально тримає.

Зверніть увагу, що$(BB')$ не перетинається$[A'C]$. Застосовуючи теорему Паша (теорема 3.4.1) для$\triangle AA'C$ і$(BB')$, отримаємо, що$(BB')$ перетинає$[AA']$; позначимо точку перетину по$M$.

Так само ми отримуємо, що$(AA')$ перетинається$[BB']$; тобто$M$ лежить на$[AA']$ і$[BB']$.

Вправа$\PageIndex{4}$

Припустимо, що точки$X$ і$Y$ лежать по протилежних сторонам від лінії$(PQ)$. Покажіть, що напівлінія$[PX)$ не перетинається$[QY)$.

Підказка

Припустимо, що$Z$ це точка перетину.

Зверніть увагу, що$Z \ne P$ і$Z \ne Q$. Тому,$Z \in (PQ)$.

Покажіть, що$Z$ і$X$ ляжте на одну сторону$(PQ)$. Повторіть аргумент, щоб показати, що$Z$ і$Y$ лежати на одній стороні$(PQ)$. Звідси випливає, що$X$ і$Y$ лежати на одній стороні$(PQ)$ - протиріччя.

Розширені вправи$\PageIndex{1}$

Зверніть увагу, що наступна кількість

\[^{~} \measuredangle ABC = \begin{cases} \pi & \text{if } \measuredangle ABC = \pi \\ -\measuredangle ABC & \text{if } \measuredangle ABC < \pi \end{cases}\]

може служити мірою кута; тобто аксіоми тримають, якщо$\measuredangle$$^{~} \measuredangle$ обмінюватися скрізь.

Покажіть, що$\measuredangle$ і$^{~} \measuredangle$ є єдиними можливими кутовими мірами на площині.
Покажіть, що без Axiom IIiC це вже не так.

Пропозиція\(\PageIndex{1}\)

Слідство\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\) Pasch's theorem