39.1: Загальні фактори

Last updated
Save as PDF

Page ID: 891

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Урок

Давайте використовувати фактори для вирішення проблем.

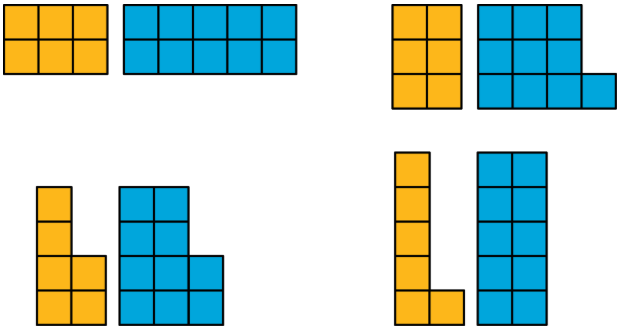
Вправа$\PageIndex{1}$: Figures Made of Squares

Як схожі пари фігур? Чим вони відрізняються?

Вправа$\PageIndex{2}$: Diego's Bake Sale

Дієго готує тістечка і печиво для продажу випічки. Він хотів би зробити мішки однакового розміру для продажу всіх 48 тістечок і 64 печива, які він має. Організуйте свою відповідь на кожне питання так, щоб за ним могли слідувати інші.

Як Дієго може упакувати всі 48 тістечок так, щоб кожен мішок мав однакову кількість з них? Скільки пакетиків він може зробити, і скільки тістечок буде в кожній сумці? Знайдіть всі можливі способи упаковки тістечок.
Як Дієго може упакувати всі 64 печива так, щоб кожен мішок мав однакову їх кількість? Скільки пакетиків він може зробити, і скільки печива буде в кожному пакетику? Знайдіть усі можливі способи пакування файлів cookie.
Як Дієго може упакувати всі 48 тістечок і 64 печива так, щоб кожен мішок мав однакову комбінацію предметів? Скільки мішків він може зробити, і скільки кожного буде в кожній сумці? Знайдіть всі можливі способи упакувати обидва пункти.
Яка найбільша кількість комбінованих сумок, які Дієго може зробити без залишку? Поясніть своєму партнерові, як ви знаєте, що це максимально можлива кількість сумок.

Вправа$\PageIndex{3}$: Greatest Common Factor

Найбільший загальний коефіцієнт 30 і 18 - 6. Як ви думаєте, що означає термін «найбільший загальний фактор»?
Знайдіть всі фактори 21 і 6. Потім визначте найбільший загальний фактор 21 і 6.
Знайдіть всі фактори 28 і 12. Потім визначають найбільший загальний фактор 28 і 12.
Прямокутна дошка оголошень 12 дюймів заввишки і 27 дюймів в ширину. Олена планує покрити його квадратами кольорового паперу, які все однакового розміру. Паперові квадрати бувають різних розмірів; всі вони мають ціле число дюймів для їх довжини сторін.
1. Яка довжина сторони найбільшого квадрата, який Олена могла використовувати для покриття дошки оголошень повністю без зазорів і нахлестов? Поясніть або покажіть свої міркування.
2. Як вирішення цієї проблеми пов'язане з найбільшим загальним фактором?

Ви готові до більшого?

Школа має 1000 шафок, всі вишикувалися в передпокої. Кожен шафка закрита. Потім.

Один студент спускається по залу і відкриває кожен шафка.
Другий учень спускається по залу і закриває кожен другий шафка: 2 шафки, 4, 6 і так далі.
Третій студент спускається по залу і змінює кожен третій шафка. Якщо шафка відкрита, він його закриває. Якщо шафка закрита, він його відкриває.
Четвертий студент спускається по залу і змінює кожен четвертий шафка.

Цей процес триває аж до тисячного учня! В кінці процесу, які шафки будуть відкриті? (Підказка: ви можете спочатку спробувати цю проблему з меншою кількістю шафок.)

Резюме

Коефіцієнт цілого числа$n$ - це ціле число, яке ділиться$n$ рівномірно без залишку. Наприклад, 1, 2, 3, 4, 6 і 12 - це всі фактори 12, оскільки кожен з них ділить 12 рівномірно і без залишку.

Загальний множник двох цілих чисел - це фактор, який вони мають спільне. Наприклад, 1, 3, 5 і 15 - фактори 45; вони також є факторами 60. Ми називаємо 1, 3, 5 і 15 загальні фактори 45 і 60.

Найбільший спільний фактор (іноді записується як GCF) двох цілих чисел - найбільший з усіх загальних факторів. Наприклад, 15 - найбільший загальний фактор для 45 і 60.

Один із способів знайти найбільший загальний коефіцієнт двох цілих чисел - це перерахувати всі фактори для кожного, а потім шукати найбільший фактор, який вони мають спільного. Спробуємо знайти найбільший спільний фактор 18 і 24. Спочатку перерахуємо всі фактори кожного числа.

Фактори 18: 1, 2, 3, 6, 9,18
Фактори 24: 1, 2, 3, 4, 6, 8, 12, 24

Загальними факторами є 1, 2, 3 та 6. З них 6 є найбільшим, тому 6 є найбільшим загальним фактором 18 і 24.

Записи глосарію

Визначення: Загальний фактор

Загальний множник двох чисел - це число, яке ділиться рівномірно на обидва числа. Наприклад, 5 є загальним фактором 15 і 20, тому що$15\div 5=3$ і$20\div 5=4$. Обидва частки, 3 і 4, є цілими числами.

Факторами 15 є 1, 3, 5 і 15.
Факторами 20 є 1, 2, 4, 5, 10 і 20.

Визначення: Найбільший спільний фактор

Найбільший спільний множник двох чисел - це найбільше число, яке ділиться рівномірно на обидва числа. Іноді ми називаємо це GCF. Наприклад, 15 - найбільший загальний фактор 45 і 60.

Факторами 45 є 1, 3, 5, 9, 15 і 45.
Факторами 60 є 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 і 60.

Практика

Вправа$\PageIndex{4}$

Викладач робить подарункові пакети. Кожен пакетик потрібно наповнити олівцями і наклейками. Вчитель має 24 олівці та 36 наклейок для використання. Кожна сумка матиме однакову кількість кожного предмета, при цьому не залишилося жодних предметів. Наприклад, вона могла виготовити 2 сумки з 12 олівцями і 18 наклейками кожен.

Які інші можливості? Поясніть або покажіть свої міркування.

Вправа$\PageIndex{5}$

Перерахуйте всі фактори 42.
Який найбільший загальний фактор 42 і 15?
Який найбільший загальний фактор 42 і 50?

Вправа$\PageIndex{6}$

Шкільний хор нараховує 90 учнів шостого класу та 75 учнів сьомого класу. Музичний керівник хоче скласти групи виконавців, з однаковим поєднанням учнів шостого та сьомого класу в кожній групі. Вона хоче сформувати якомога більше груп.

Яка найбільша кількість груп, які можна було б сформувати? Поясніть або покажіть свої міркування.
Якщо буде сформовано стільки груп, скільки учнів кожного класу було б у кожній групі?

Вправа$\PageIndex{7}$

Ось кілька банківських операцій з банківського рахунку минулого тижня. Які операції представляють негативні значення?

Понеділок: $650 зарплата депозитується

Вівторок: 40 доларів зняття з банкомату на газовому насосі

Середа: $20 кредит на повернутий товар

Четвер: $125 віднімається за плату стільникового телефону

П'ятниця: $45 чек написаний для оплати замовлення книги

Субота: 80 доларів на вихідні витрати грошей

Неділя: $10 грошова винагорода, внесена від компанії кредитної картки

(З блоку 7.3.3)

Вправа$\PageIndex{8}$

Знайдіть коефіцієнти.

$\frac{1}{7}\div\frac{1}{8}$
$\frac{12}{5}\div\frac{6}{5}$
$\frac{1}{10}\div 10$
$\frac{9}{10}\div\frac{10}{9}$

(Від блоку 4.3.2)

Вправа$\PageIndex{9}$

Слон може подорожувати з постійною швидкістю 25 миль на годину, в той час як жираф може подорожувати з постійною швидкістю 16 миль на$\frac{1}{2}$ годину.

Яка тварина біжить швидше? Поясніть свої міркування.
Як далеко кожна тварина може пробігти за 3 години?

(Від блоку 2.3.4)