Skip to main content
LibreTexts - Ukrayinska

18.3: Контрольні відсотки

  1. Last updated
  2. Save as PDF
  • Page ID
    833

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте контрастуємо відсотки і дроби.

    Вправа\(\PageIndex{1}\): What Percentage is Shaded?

    Який відсоток кожної діаграми затінюється?

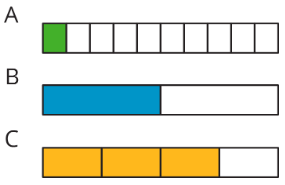
    clipboard_e7048f56bfa8304eda735b7c9a4a3ca4a.png
    Малюнок\(\PageIndex{1}\)

    Вправа\(\PageIndex{2}\): Liters, Meters, and Hours

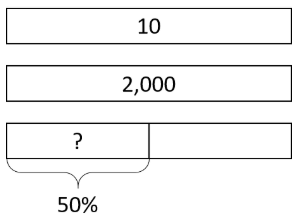
      1. Скільки становить 50% від 10 літрів молока?
      2. Як далеко 50% від 2,000-кілометрової поїздки?
      3. Скільки триває 50% від 24-годинного дня?
      4. Як можна знайти 50% від будь-якого числа?
      1. Як далеко 10% від 2,000-кілометрової поїздки?
      2. Скільки 10% від 10 літрів молока?
      3. Скільки триває 10% від 24-годинного дня?
      4. Як можна знайти 10% від будь-якого числа?
      1. Скільки триває 75% 24-годинного дня?
      2. Як далеко 75% від 2,000-кілометрової поїздки?
      3. Скільки становить 75% з 10 літрів молока?
      4. Як знайти 75% будь-якого числа?
    clipboard_eb0901d766e6a06efd4d6ff6ffd93dfaa.png
    Малюнок\(\PageIndex{2}\)

    Вправа\(\PageIndex{3}\): Nine is ...

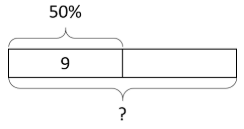
    Поясніть, як можна розрахувати кожне значення подумки.

    1. 9 - це 50% від якого числа?
    2. 9 це 25% від якого числа?
    3. 9 - це 10% від якого числа?
    4. 9 - це 75% від якого числа?
    5. 9 - це 150% від якого числа?
    clipboard_e93611f83aab169f95632d5838a26a63f.png
    Малюнок\(\PageIndex{3}\)

    Вправа\(\PageIndex{4}\): Matching the Percentage

    Зіставте відсоток, який описує співвідношення між кожною парою чисел. Один відсоток залишиться. Будьте готові пояснити свої міркування.

    1. 7 - це який відсоток 14?
    2. 5 - це який відсоток 20?
    3. 3 - це який відсоток 30?
    4. 6 - це який відсоток 8?
    5. 20 - це який відсоток 5?
    • 4%
    • 10%
    • 25%
    • 50%
    • 75%
    • 400%

    Ви готові до більшого?

    1. Який відсоток від нинішнього населення світу становить у віці до 14 років?
    2. Скільки це людей?
    3. Скільки людей 14 років і старше?

    Резюме

    Певні відсотки легко подумати з точки зору дробів.

    clipboard_e1531887c0a7cae5b9ec2a648c7ac4823.png
    Малюнок\(\PageIndex{4}\): Подвійний числовий рядок з 5 рівномірно розташованими галочками. Галочки у верхньому цифровому рядку позначені 0, одна четверта рази x, півтора рази x, три четверті рази x та x. Галочки на нижньому рядку позначені 0 відсотків, 25 відсотків, 50 відсотків, 75 відсотків і 100 відсотків.
    • 25% числа завжди\(\frac{1}{4}\) від цього числа.
      Наприклад, 25% з 40 літрів - це\(\frac{1}{4}\cdot 40\) або 10 літрів.
    • 50% числа завжди\(\frac{1}{2}\) від цього числа.
      Наприклад, 50% з 82 кілометрів\(\frac{1}{2}\cdot 82\) або 41 кілометр.
    • 75% числа завжди це\(\frac{3}{4}\) число.
      Наприклад, 75% від 1 фунта становить\(\frac{3}{4}\) фунт.
    • 10% числа завжди\(\frac{1}{10}\) від цього числа.
      Наприклад, 10% з 95 метрів - це 9,5 метра.
    • Ми також можемо знайти кратні 10% за допомогою десятих.
      Наприклад, 70% числа завжди\(\frac{7}{10}\) це число, тому 70% з 30 днів\(\frac{7}{10}\cdot 30\) або 21 день.
    clipboard_efc9a1233bc8b5436d332a44546c56f0d.png
    Малюнок\(\PageIndex{5}\): Подвійний числовий рядок з 11 рівномірно розташованими галочками. Для верхнього числового рядка число 0 знаходиться на першій галочці, одна десята - x на другій, сім десятих разів x на восьмій, а x на одинадцятій. Решта галочки порожні. У нижньому рядку номера, починаючи з першої позначки, позначені нульові відсотки, 10 відсотків, 20 відсотків, 30 відсотків, 40 відсотків, 50 відсотків, 60 відсотків, 70 відсотків, 80 відсотків, 90 і 100 відсотків.

    Записи глосарію

    Визначення: Відсоток

    Слово відсоток означає «на кожні 100». Символ відсотка -%.

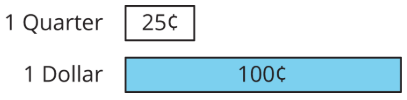
    Наприклад, чверть коштує 25 центів, а долар коштує 100 центів. Можна сказати, що чверть коштує 25% від долара.

    clipboard_e2d93f86aa3d92a7b944d17c0661fecf5.png
    Малюнок\(\PageIndex{6}\)
    clipboard_e638565d83ec434582c9736e062f533b7.png
    Малюнок\(\PageIndex{7}\): Схема з двох брусків з різною довжиною. Верхня панель позначена 1 Чверть і 25 центів позначено всередині бару. Нижня планка позначена позначкою 1 Долар. Це в 4 рази довше верхньої панелі і 100 центів позначено всередині бару.

    Визначення: Відсоток

    Відсоток - це ставка на 100.

    Наприклад, акваріум може вмістити 36 літрів. Прямо зараз в баку 27 літрів води. Відсоток бака, який заповнений, становить 75%.

    clipboard_efec317f953e46323cecd8f9318ef59a3.png
    Малюнок\(\PageIndex{8}\)

    Практика

    Вправа\(\PageIndex{5}\)

    1. Як можна швидко знайти 50% числа в голові?
    2. Андре живе в 1,6 км від школи. Що таке 50% від 1,6 км?
    3. Дієго живе за\(\frac{1}{2}\) милю від школи. Що таке 50%\(\frac{1}{2}\) милі?

    Вправа\(\PageIndex{6}\)

    На портативних комп'ютерах діє знижка 10%. Якщо хтось економить 35 доларів на ноутбуці, якою була його первісна вартість? Якщо ви застрягли, подумайте про використання таблиці.

    економія (долари) відсоток
    \(35\) \(10\)
    \(?\) \(100\)
    Таблиця\(\PageIndex{1}\)

    Вправа\(\PageIndex{7}\)

    Поясніть, як розрахувати їх подумки.

    1. 15 - це який відсоток 30?
    2. 3 - це який відсоток 12?
    3. 6 - це який відсоток 10?

    Вправа\(\PageIndex{8}\)

    Ной каже, що щоб знайти 20% числа, він ділить число на 5. Наприклад, 20% з 60 - це 12, тому що\(60\div 5=12\). Чи завжди працює метод Ноя? Поясніть, чому чи чому ні.

    Вправа\(\PageIndex{9}\)

    Дієго має 75% від $10. Ной має 25% від 30 доларів. Дієго вважає, що у нього більше грошей, ніж Ной, але Ной вважає, що вони мають рівну суму грошей. Хто правий? Поясніть свої міркування.

    (Від блоку 3.4.1)

    Вправа\(\PageIndex{10}\)

    Лін і Андре починають ходити один до одного одночасно з протилежних кінців 22-мильної пішохідної стежки. Лінь ходить зі швидкістю 2,5 милі на годину. Андре ходить зі швидкістю 3 милі на годину.

    Ось таблиця, що показує пройдені відстані і наскільки далеко один від одного Лін і Андре були з часом. Використовуйте таблицю, щоб дізнатися, скільки часу проходить, перш ніж вони зустрінуться.

    минув час (година) Відстань Лінь (милі) Відстань Андре (милі) відстань один від одного (милі)
    \(0\) \(0\) \(0\) \(22\)
    \(1\) \(2.5\) \(3\) \(16.5\)
    Таблиця\(\PageIndex{2}\)

    (Від блоку 3.3.4)