Skip to main content
LibreTexts - Ukrayinska

9.2: Представлення коефіцієнтів за допомогою діаграм

  1. Last updated
  2. Save as PDF
  • Page ID
    970

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте скористаємося діаграмами для представлення коефіцієнтів.

    Вправа\(\PageIndex{1}\): Number Talk: Dividing \(4\) and Multiplying by \(\frac{1}{4}\)

    Знайти значення кожного виразу подумки.

    1. \(24\div 4\)
    2. \(\frac{1}{4}\cdot 24\)
    3. \(24\cdot\frac{1}{4}\)
    4. \(5\div 4\)

    Вправа\(\PageIndex{2}\): A Collection of Snap Cubes

    Ось колекція оснащення кубиків.

    clipboard_e716a5366372c0ca87bb02c511409a29b.png
    Малюнок\(\PageIndex{1}\)
    1. Виберіть два кольори на зображенні та намалюйте діаграму, яка показує кількість кубиків оснащення для цих двох кольорів.
    2. Торгові папери з партнером. На їх папері напишіть пропозицію, щоб описати співвідношення, показане на їх схемі. Ваш партнер зробить те ж саме для вашої діаграми.
    3. Поверніть папір партнера. Прочитайте речення, написане на вашому папері. Якщо ви не згодні, поясніть своє мислення.

    Вправа\(\PageIndex{3}\): Blue Paint and Art Paste

    Олена змішала 2 склянки білої фарби з 6 столовими ложками блакитної фарби.

    Ось діаграма, яка представляє цю ситуацію.

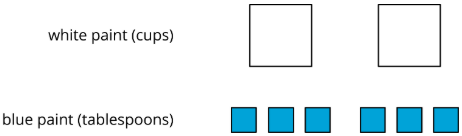
    clipboard_ed17499b73ab61c14fdf90abb235056e3.png
    Малюнок\(\PageIndex{2}\): Дискретна діаграма квадратів, які представляють кількість фарби. Верхній ряд позначений білою фарбою, в стаканчиках і містить 2 великих квадрата. Нижній ряд позначений синьою фарбою, в столових ложках і містить 6 маленьких квадратиків.
    1. Обговоріть кожне твердження, і обведіть всі ті, які правильно описують цю ситуацію. Переконайтеся, що і ви, і ваш партнер згодні з кожною обведеною відповіддю.
      1. Співвідношення чашок білої фарби до столових ложок блакитної фарби становить\(2:6\).
      2. На кожну чашку білої фарби йде 2 столові ложки блакитної фарби.
      3. На кожні 3 столові ложки блакитної фарби припадає 1 склянка білої фарби.
      4. На кожну чашку білої фарби припадає 3 столові ложки блакитної фарби.
      5. На кожну столову ложку блакитної фарби йде 3 склянки білої фарби.
      6. На кожні 6 столових ложок блакитної фарби припадає 2 склянки білої фарби.
      7. Співвідношення столових ложок блакитної фарби до чашок білої фарби становить 6 до 2.
    2. Джада змішала 8 склянок борошна з 2 пінтами води, щоб зробити пасту для художнього проекту.
      1. Намалюйте схему, яка представляє ситуацію.
      2. Напишіть хоча б два пропозиції, що описують співвідношення борошна і води.

    Вправа\(\PageIndex{4}\): Card Sort: Spaghetti Sauce

    Ваш вчитель дасть вам карти з описом різних рецептів соусу для спагетті. На схемах:

    • коло являє собою чашку томатного соусу
    • квадрат являє собою столову ложку олії
    • трикутник являє собою чайну ложку орегано
    clipboard_ed7ae3532c5cfc7b5aa82ed486510194d.png
    Малюнок\(\PageIndex{3}\): Соус для спагетті, їдять кіш. КУБ.СМ НА 2,0. Flickr. Джерело.
    1. По черзі зі своїм партнером, щоб зіставити речення зі схемою.
      1. Для кожного матчу, який ви знайдете, поясніть своєму партнерові, як ви знаєте, що це матч.
      2. Для кожного матчу, який знайде ваш партнер, уважно слухайте їх пояснення. Якщо ви не згодні, обговоріть своє мислення і працюйте, щоб досягти згоди.
    2. Після того, як ви і ваш партнер домовилися про всі матчі, перевірте свої відповіді ключем відповіді. Якщо є якісь помилки, обговоріть, чому і перегляньте свої матчі.
    3. Існували дві діаграми, кожна з яких збігалася з двома різними реченнями. Якими вони були?
      • Діаграма _______ збігається з обома реченнями ______ і ______.
      • Діаграма _______ збігається з обома реченнями ______ і ______.
    4. Виберіть одну з інших діаграм і придумайте ще одне речення, яке могло б описати співвідношення, показане на схемі.

    Ви готові до більшого?

    Створіть діаграму, яка представляє будь-яке співвідношення в рецепті на ваш вибір. Чи можна включити більше 2 інгредієнтів у вашій схемі?

    Резюме

    Співвідношення можна представити за допомогою діаграм. На діаграмах не потрібно включати реалістичні деталі. Наприклад, рецепт лимонаду говорить: «Змішайте 2 ложки порошку лимонаду з 6 склянками води».

    Замість цього:

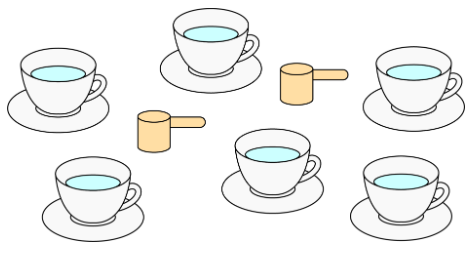
    clipboard_ecee9cf721516d68ace69ab5baee52041.png
    Малюнок\(\PageIndex{4}\)

    Ми можемо намалювати щось на зразок цього:

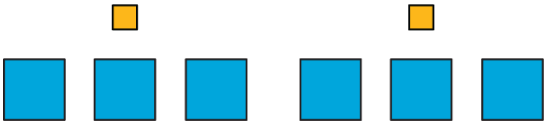
    clipboard_efcfd2cec9af20a13c8471c01a4a77c04.png
    Малюнок\(\PageIndex{5}\)

    На цій схемі видно, що співвідношення чашок води до совок порошку лимонаду становить 6 до 2. Ми також бачимо, що на кожну мірну ложку порошку лимонаду припадає 3 склянки води.

    Записи глосарію

    Визначення: Співвідношення

    Співвідношення - це зв'язок між двома або більше величинами.

    Наприклад, співвідношення\(3:2\) може описати рецепт, який використовує 3 склянки борошна на кожні 2 яєць, або човен, який рухається по 3 метри кожні 2 секунди. Одним із способів представлення співвідношення\(3:2\) є діаграма, яка має 3 синіх квадратів для кожних 2 зелених квадратів.

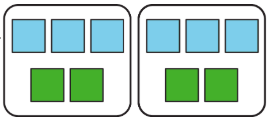
    clipboard_ea9b143595346d0fb6df303cb0916cf87.png
    Малюнок\(\PageIndex{6}\)

    Практика

    Вправа\(\PageIndex{5}\)

    Ось схема, яка описує чашки зеленої і білої фарби в суміші.

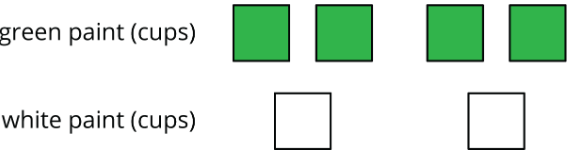
    clipboard_ebc02d842f503198e3c7f21fbb1df2f78.png
    Малюнок\(\PageIndex{7}\): Схема квадратів, які представляють кількість чашок фарби. Верхній ряд позначений зеленою фарбою, в стаканчиках і містить 4 зелених квадрата. Нижній ряд позначений білою фарбою, в стаканчиках і містить 2 білих квадрата.

    Виберіть всі твердження, які правильно описують цю діаграму.

    1. Співвідношення чашок білої фарби до чашок зеленої фарби становить 2 до 4.
    2. На кожну чашку зеленої фарби припадає дві чашки білої фарби.
    3. Співвідношення чашок зеленої фарби до чашок білої фарби становить\(4:2\).
    4. На кожну чашку білої фарби припадає дві чашки зеленої фарби.
    5. Співвідношення чашок зеленої фарби до чашок білої фарби становить\(2:4\).

    Вправа\(\PageIndex{6}\)

    Щоб зробити закусочну суміш, з'єднайте 2 склянки родзинок з 4 склянками кренделів і 6 склянками мигдалю.

    1. Створіть діаграму для представлення кількості кожного інгредієнта в цьому рецепті.
    2. Використовуйте свою діаграму, щоб завершити кожне речення.
      • Співвідношення ______________ до __________________ до __________________ становить ________: ________: ________.
      • На кожну чашку родзинок припадає ________ чашок кренделів.
      • На кожну чашку родзинок припадає ________ чашок мигдалю.

    Вправа\(\PageIndex{7}\)

    1. Квадрат становить 3 дюйми на 3 дюйми. Яка його площа?
    2. Квадрат має довжину сторони 5 футів. Яка його площа?
    3. Площа квадрата становить 36 квадратних сантиметрів. Яка довжина кожної сторони квадрата?

    (Від одиниці 1.6.1)

    Вправа\(\PageIndex{8}\)

    Знайдіть площу цього чотирикутника. Поясніть або покажіть свою стратегію.

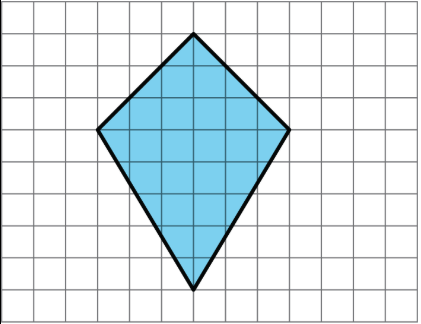
    clipboard_e668779635878935eb36c7f448e26af12.png
    Малюнок\(\PageIndex{8}\)

    (Від блоку 1.4.1)

    Вправа\(\PageIndex{9}\)

    Заповніть кожне рівняння числом, яке робить його істинним.

    1. \(\frac{1}{8}\cdot 8=\underline{\qquad}\)
    2. \(\frac{3}{8}\cdot 8=\underline{\qquad}\)
    1. \(\frac{1}{8}\cdot 7=\underline{\qquad}\)
    2. \(\frac{3}{8}\cdot 7=\underline{\qquad}\)

    (З блоку 2.1.1)