9.1: Введення коефіцієнтів і співвідношення мови
Урок
Опишемо дві величини одночасно.
Вправа9.1.1: What Kind and How Many?
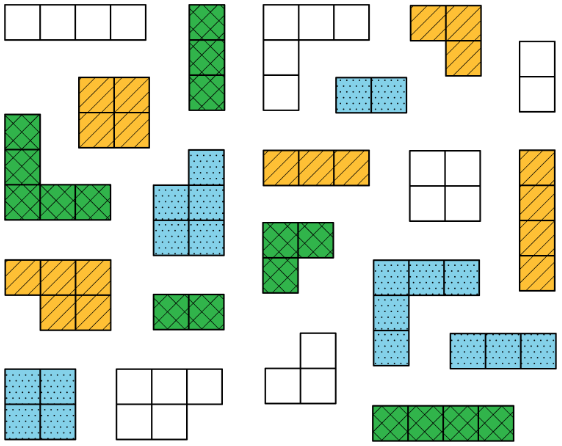
Подумайте про різні способи сортування цих цифр. Які категорії ви могли б використовувати? Скільки груп у вас було б?
Вправа9.1.2: The Teacher's Collection
- Подумайте, як сортувати колекцію вчителя на дві-три категорії. Підрахуйте елементи в кожній категорії, і запишіть інформацію в таблицю.
| назва категорії | |||
|---|---|---|---|
| категорія сума |
Пауза тут, щоб ваш викладач міг переглянути вашу роботу.
- Напишіть принаймні два речення, які описують співвідношення в збірнику. Пам'ятайте, існує безліч способів написання співвідношення:
- Співвідношення однієї категорії до іншої категорії становить ________ до ________.
- Співвідношення однієї категорії до іншої категорії - ________: ________.
- Є _______ однієї категорії на кожен _______ іншої категорії.
Вправа9.1.3: The Student's Collection
- Сортуйте свою колекцію за трьома категоріями. Можна експериментувати з різними способами розстановки цих категорій. Потім порахуйте елементи в кожній категорії, і запишіть інформацію в таблицю.
| назва категорії | |||
|---|---|---|---|
| категорія сума |
- Напишіть принаймні два речення, які описують співвідношення в збірнику. Пам'ятайте, існує безліч способів написання співвідношення:
- Співвідношення однієї категорії до іншої категорії становить ________ до ________.
- Співвідношення однієї категорії до іншої категорії - ________: ________.
- Є _______ однієї категорії на кожен _______ іншої категорії.
Пауза тут, щоб ваш вчитель міг переглянути ваші речення.
- Зробіть наочне відображення ваших предметів, що чітко показує одне з ваших тверджень. Будьте готові поділитися своїм дисплеєм з класом.
Ви готові до більшого?
- Використовуйте два кольори, щоб затінювати прямокутник, так що на кожну 1 квадратну одиницю іншого кольору є 2 квадратні одиниці одного кольору.
- Прямокутник, який ви щойно пофарбували, має площу 24 квадратних одиниць. Намалюйте іншу форму, яка не має площі 24 квадратних одиниць, але її також можна затінювати двома кольорами у2:1 співвідношенні. Розтушуйте нову форму, використовуючи два кольори.
Резюме
Співвідношення - це зв'язок між двома або більше величинами. Існує безліч способів описати ситуацію з точки зору співвідношень. Наприклад, подивіться на цю колекцію:
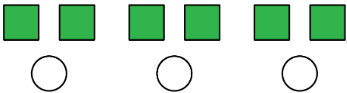
Ось кілька правильних способів опису колекції:
- Співвідношення квадратів до кіл дорівнює6:3.
- Співвідношення кіл до квадратів - 3 до 6.
Зверніть увагу, що фігури можуть бути розташовані в рівних групах, що дозволяє нам описувати фігури за допомогою інших чисел.
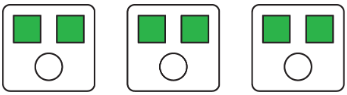
- Є 2 квадрата на кожен 1 коло.
- На кожні 2 квадрати припадає 1 коло.
Записи глосарію
Визначення: Співвідношення
Співвідношення - це зв'язок між двома або більше величинами.
Наприклад, співвідношення3:2 може описати рецепт, який використовує 3 склянки борошна на кожні 2 яєць, або човен, який рухається по 3 метри кожні 2 секунди. Одним із способів представлення співвідношення3:2 є діаграма, яка має 3 синіх квадратів для кожних 2 зелених квадратів.
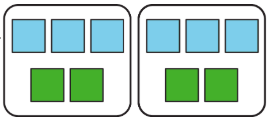
Практика
Вправа9.1.4
У кошику з фруктами 9 бананів, 4 яблука, 3 сливи.
- Співвідношення бананів до яблук - ________: ________.
- Співвідношення слив до яблук становить ________ до ________.
- На кожні ________ яблука припадає ________ сливи.
- На кожні 3 банана припадає один ________.
Вправа9.1.5
Доповніть пропозиції, щоб описати цю картину.

- Співвідношення собак до кішок - ________.
- На кожну ________ собак припадає ________ кішок.
Вправа9.1.6
Напишіть два різних речення, які використовують співвідношення для опису кількості очей і ніг на цій картинці.

Вправа9.1.7
Виберіть відповідну одиницю виміру для кожної кількості.
- площа прямокутника
- об'єм призми
- сторона квадрата
- площа квадрата
- об'єм куба
- см
- см 3
- см 2
(Від одиниці 1.6.1)
Вправа9.1.8
Знайдіть об'єм і площу поверхні кожної призми.
- Призма А: 3 см х 3 см на 3 см

- Призма B: 5 см на 5 см на 1 см

- Порівняйте обсяги призм, а потім їх площі поверхні. Чи має призма з більшим об'ємом також більшу площу поверхні?
(Від одиниці 1.5.5)
Вправа9.1.9
Яка фігура являє собою трикутну призму? Виберіть все, що застосовується.
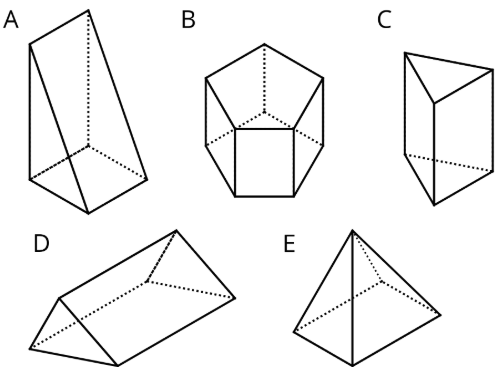
- A
- Б
- C
- D
- Е
(Від одиниці 1.5.2)
