12.5: Біноміальна теорема
- Page ID
- 59439
До кінця цього розділу ви зможете:
- Використовуйте трикутник Паскаля, щоб розширити біном
- Оцініть біноміальний коефіцієнт
- Використовуйте біноміальну теорему для розширення біноміального
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
Якщо ви пропустили цю проблему, перегляньте приклад 1.25. - Розгорнути:\((3 x+5)^{2}\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.32. - Розгорнути:\((x-y)^{2}\).
Якщо ви пропустили цю проблему, перегляньте приклад 5.32.
Використовуйте трикутник Паскаля, щоб розширити біноміал
У нашій попередній роботі ми склали біноміали у квадраті або за допомогою FOIL, або за допомогою шаблону біноміальних квадратів. Можна також сказати, що ми розширили\((a+b)^{2}\).
\((a+b)^{2}=a^{2}+2 a b+b^{2}\)
Щоб розширити\((a+b)^{3}\), ми визнаємо, що це\((a+b)^{2}(a+b)\) і примножуємо.
\((a+b)^{3}\)
\((a+b)^{2}(a+b)\)
\(\left(a^{2}+2 a b+b^{2}\right)(a+b)\)
\(a^{3}+2 a^{2} b+a b^{2}+a^{2} b+2 a b^{2}+b^{3}\)
\(a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
\((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\)
Щоб знайти менш виснажливий метод, який буде працювати для вищих розширень\((a+b)^{7}\), як, ми знову шукаємо закономірності в деяких розширеннях.
| Кількість термінів | Перший семестр | Останній термін | |
|---|---|---|---|
| \((a+b)^{1}=a+b\) | \(2\) | \(a^{1}\) | \(b^{1}\) |
| \((a+b)^{2}=a^{2}+2 a b+b^{2}\) | \(3\) | \(a^{2}\) | \(b^{2}\) |
| \((a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\) | \(4\) | \(a^{3}\) | \(b^{3}\) |
| \((a+b)^{4}=a^{4}+4 a^{3} b+6 a^{2} b^{2}+4 a b^{3}+b^{4}\) | \(5\) | \(a^{4}\) | \(b^{4}\) |
| \((a+b)^{5}=a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}\) | \(6\) | \(a^{5}\) | \(b^{5}\) |
| \((a+b)^{n}\) | \(n\) | \(a^{n}\) | \(b^{n}\) |
Зверніть увагу, що перший і останній терміни показують лише одну змінну. Нагадаємо\(a^{0}=1\), що, щоб ми могли переписати перший і останній терміни, щоб включити обидві змінні. Наприклад, ми могли б розширити,\((a+b)^{3}\) щоб показати кожен термін з обома змінними.
Як правило, ми не показуємо нульові показники, так само, як ми зазвичай пишемо,\(x\) а не\(1x\).
Шаблони в розширенні\((a+b)^{n}\)
- Кількість термінів - це\(n+1\).
- Перший термін -\(a^{n}\) і останній термін -\(b^{n}\).
- Показники на\(a\) зменшення на одиницю на кожен термін йде зліва направо.
- Показники\(b\) збільшення на одиницю на кожен термін йде зліва направо.
- Сума показників на будь-якому терміні дорівнює\(n\).
Давайте розглянемо приклад, щоб виділити три останні візерунки.
З шаблонів, які ми визначили, ми бачимо змінні в розширенні\((a+b)^{n}\), буде
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}\).
Щоб знайти коефіцієнти членів, записуємо наші розширення знову орієнтуючись на коефіцієнти. Переписуємо коефіцієнти вправо, утворюючи масив коефіцієнтів.
Масив праворуч називається трикутником Паскаля. Зверніть увагу, що кожне число в масиві є сумою двох найближчих чисел у рядку вище. Ми можемо знайти наступний рядок, починаючи і закінчуючи одним, а потім додаючи два сусідніх числа.
Цей трикутник дає коефіцієнти членів, коли ми розширюємо біноми.
Трикутник Паскаля
У наступному прикладі ми будемо використовувати цей трикутник і шаблони, які ми розпізнали, щоб розширити біном.
Використовуйте трикутник Паскаля, щоб розширити\((x+y)^{6}\).
Рішення:
Ми знаємо, що змінні для цього розширення будуть слідувати шаблону, яку ми визначили. Ненульові показники\(x\) будуть починатися з шести і зменшуватися до одиниці. Ненульові показники\(y\) будуть починатися з одиниці і збільшуватися до шести. Сума показників у кожному семестрі буде шість. У нашій викрійці,\(a=x\) і\(b=y\).
\(\begin{array}{l}{(a+b)^{n}=a^{n}+\_\_\_a^{n-1} b^{1}+\_\_\_a^{n-2} b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n}} \\ {(x+y)^{6}=x^{6}+\_\_\_x^{5} y^{1}+\_\_\_x^{4} y^{2}+\_\_\_x^{3} y^{3}+\_\_\_x^{2} y^{4}+\_\_\_x^{1} y^{5}+y^{6}}\end{array}\)
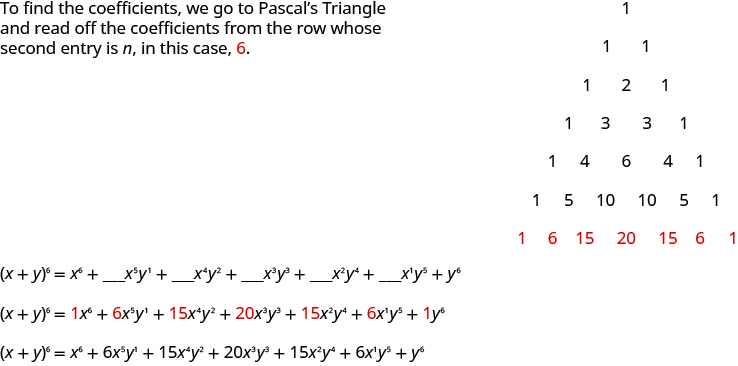
Використовуйте трикутник Паскаля, щоб розширити\((x+y)^{5}\).
- Відповідь
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Використовуйте трикутник Паскаля, щоб розширити\((p+q)^{7}\).
- Відповідь
-
\(\begin{array}{c}{p^{7}+7 p^{6} q+21 p^{5} q^{2}+35 p^{4} q^{3}} {+35 p^{3} q^{4}+21 p^{2} q^{5}+7 p q^{6}+q^{7}}\end{array}\)
У наступному прикладі ми хочемо розширити біном з однією змінною і однією константою. Нам потрібно визначити\(a\) і акуратно\(b\) нанести візерунок.
Використовуйте трикутник Паскаля, щоб розширити\((x+3)^{5}\).
Рішення:
Визначаємо\(a\) і по\(b\) викрійці.
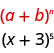
У нашій викрійці,\(a=x\) і\(b=3\).
Ми знаємо, що змінні для цього розширення будуть слідувати шаблону, яку ми визначили. Сума показників у кожному семестрі буде п'ять.
\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((x+3)^{5}=x^{5}+\_\_\_x^{4}\cdot3^{1}+\_\_\_x^{3}\cdot3^{2}+\_\_\_x^{2}\cdot3^{3}+\_\_\_x^{1}\cdot3^{4}+3^{5}\)

Використовуйте трикутник Паскаля, щоб розширити\((x+2)^{4}\).
- Відповідь
-
\(x^{4}+8 x^{3}+24 x^{2}+32 x+16\)
Використовуйте трикутник Паскаля, щоб розширити\((x+1)^{6}\).
- Відповідь
-
\(\begin{array}{l}{x^{6}+6 x^{5}+15 x^{4}+20 x^{3}+15 x^{2}} {+6 x+1}\end{array}\)
У наступному прикладі біном є різниця, а перший член має постійну раз змінну. Після того, як ми виявимо\(b\) кінець візерунка, ми повинні ще раз акуратно нанести візерунок.\(a\)
Використовуйте трикутник Паскаля, щоб розширити\((3x-2)^{4}\).
Рішення:
Визначаємо\(a\) і по\(b\) викрійці.
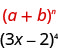
У нашій викрійці,\(a=3x\) і\(b=-2\).

\((a+b)^{n}=a^{n}+\_\_\_a^{n-1}b^{1}+\_\_\_a^{n-2}b^{2}+\ldots+\_\_\_a^{1}b^{n-1}+b^{n} \)
\((3 x-2 )^{4}=1 \cdot\left(\stackrel{3}{x}+4(3 x)^{3}(-2)^{1}+6(3 x)^{2}(-2)^{2}+4(3 x)^{1}(-2)^{3}+1 \cdot(-2)^{4}\right.\)
\((3 x-2)^{4}=81 x^{4}+4\left(27 x^{3}\right)(-2)+6\left(9 x^{2}\right)(4)+4(3 x)(-8)+1 \cdot 16\)
\((3 x-2 )^{4}=81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)
Використовуйте трикутник Паскаля, щоб розширити\((2x-3)^{4}\).
- Відповідь
-
\(16 x^{4}-96 x^{3}+216 x^{2}-216 x+81\)
Використовуйте трикутник Паскаля, щоб розширити\((2x-1)^{6}\).
- Відповідь
-
\(\begin{array}{l}{64 x^{6}-192 x^{5}+240 x^{4}-160 x^{3}} {+60 x^{2}-12 x+1}\end{array}\)
Оцініть біноміальний коефіцієнт
Хоча трикутник Паскаля є одним із методів розширення біноміалу, ми також розглянемо інший метод. Перш ніж ми перейдемо до цього, нам потрібно ввести ще кілька факторіальних позначень. Це позначення використовується не тільки для розширення біноміалів, але і при вивченні та використанні ймовірності.
Щоб знайти коефіцієнти членів розширених біноміалів, нам потрібно буде вміти оцінювати позначення,\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) яке називається біноміальним коефіцієнтом. Читаємо\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) як «\(n\)вибрати\(r\)» або «\(n\)\(r\)взято за раз».
Біноміальний коефіцієнт\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), де\(r\) і\(b\) є цілими числами з\(0 \leq r \leq n\), визначається як
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Ми читаємо\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) як «\(n\)вибрати\(r\)» або «\(n\)\(r\)взято за раз».
Оцініть:
- \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
- \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Рішення:
а. скористаємося визначенням біноміального коефіцієнта,
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
Використовуйте визначення\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), де\(n=5, r=1\).
\(\frac{5 !}{1 !(5-1) !}\)
Спростити.
\(\frac{5 !}{1 !(4) !}\)
Перепишіть\(5!\) як\(5\cdot 4!\)
\(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)
Спростити, видаливши загальні фактори.
\(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)
Спростити.
\(5\)
\(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)
б.\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)
Використовуйте визначення\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), де\(n=7, r=7\).
\(\frac{7 !}{7 !(7-7) !}\)
Спростити.
\(\frac{7 !}{7 !(0) !}\)
Спростити. Пам'ятайте\(0!=1\).
\(1\)
\(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)
c.\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)
Використовуйте визначення\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), де\(n=4, r=0\).
\(\frac{4 !}{0 !(4-0) !}\)
Спростити.
\(\frac{4 !}{0 !(4) !}\)
Спростити.
\(1\)
\(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)
д.\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)
Використовуйте визначення\(\left( \stackrel{5}{1}\right)=\frac{n !}{r !(n-r) !}\), де\(n=8, r=5\).
\(\frac{8 !}{5 !(8-5) !}\)
Спростити.
\(\frac{8 !}{5 !(3) !}\)
Перепишіть\(8!\) як\(8\cdot 7\cdot 6\cdot 5!\) і видаліть загальні фактори.
\(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1}\)
Спростити.
\(56\)
\(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)
Оцініть кожен біноміальний коефіцієнт:
- \(\left( \begin{array}{l}{6} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{8} \\ {8}\end{array}\right)\)
- \(\left( \begin{array}{l}{5} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{7} \\ {3}\end{array}\right)\)
- Відповідь
-
- \(6\)
- \(1\)
- \(1\)
- \(35\)
Оцініть кожен біноміальний коефіцієнт:
- \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right)\)
- \(\left( \begin{array}{l}{11} \\ {11}\end{array}\right)\)
- \(\left( \begin{array}{l}{9} \\ {0}\end{array}\right)\)
- \(\left( \begin{array}{l}{6} \\ {5}\end{array}\right)\)
- Відповідь
-
- \(2\)
- \(1\)
- \(1\)
- \(6\)
У попередньому прикладі\((a)\)\((b)\),\((c)\) продемонструвати деякі особливі властивості біноміальних коефіцієнтів.
Властивості біноміальних коефіцієнтів
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
Використовуйте біноміальну теорему для розширення біноміалу
Тепер ми готові використовувати альтернативний метод розширення біноміалів. Біноміальна теорема використовує ту саму закономірність для змінних, але використовує біноміальний коефіцієнт для коефіцієнта кожного члена.
Біноміальна теорема
Для будь-яких дійсних чисел\(a\) і\(b\), і натуральних чисел\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Використовуйте Біноміальну теорему для розширення\((p+q)^{4}\).
Рішення:
Визначаємо\(a\) і по\(b\) викрійці.
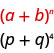
У нашій викрійці,\(a=p\) і\(b=q\).
Використовуємо біноміальну теорему.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Підставляємо в значення\(a=p, b=q\) і\(n=4\).
\((p+q)^{4}=\left( \begin{array}{c}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{4-1} q^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{4-2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p^{4-3} q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Спростіть показники.
\((p+q)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right) p^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right) p^{3} q+\left( \begin{array}{c}{4} \\ {2}\end{array}\right) p^{2} q^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right) p q^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) q^{4}\)
Оцініть коефіцієнти, пам'ятайте,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((p+q)^{4}=1 p^{4}+4 p^{3} q^{1}+\frac{4 !}{2 !(2) !} p^{2} q^{2}+\frac{4 !}{3 !(4-3) !} p^{1} q^{3}+1 q^{4}\)
\((p+q)^{4}=p^{4}+4 p^{3} q+6 p^{2} q^{2}+4 p q^{3}+q^{4}\)
Використовуйте Біноміальну теорему для розширення\((x+y)^{5}\).
- Відповідь
-
\(\begin{array}{l}{x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}} {+5 x y^{4}+y^{5}}\end{array}\)
Використовуйте Біноміальну теорему для розширення\((m+n)^{6}\).
- Відповідь
-
\(\begin{array}{l}{m^{6}+6 m^{5} n+15 m^{4} n^{2}+20 m^{3} n^{3}} {+15 m^{2} n^{4}+6 m n^{5}+n^{6}}\end{array}\)
Зверніть увагу, що коли ми розширили\((p+q)^{4}\) в останньому прикладі, використовуючи Біноміальну теорему, ми отримали ті самі коефіцієнти, які ми отримали б від використання трикутника Паскаля.
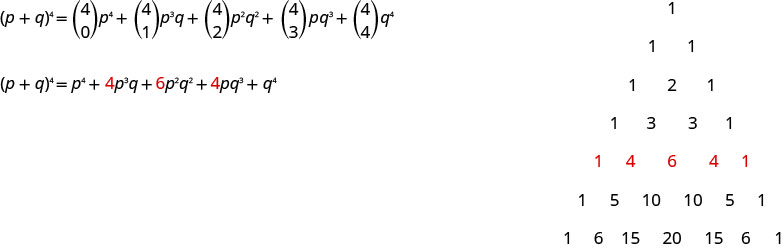
Наступний приклад, біноміал - це різниця. Коли біноміал - це різниця, ми повинні бути обережними у визначенні значень, які ми будемо використовувати у шаблоні.
Використовуйте Біноміальну теорему для розширення\((x-2)^{5}\).
Рішення:
Визначаємо\(a\) і по\(b\) викрійці.
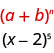
У нашій викрійці,\(a=x\) і\(b=-2\).
Використовуємо біноміальну теорему.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Підставляємо в значення\(a=x, b=-2\), і\(n=5\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{5-1}(-2)^{1}+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{5-2}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{5-3}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x^{5-4}(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
Спростити коефіцієнти. Пам'ятайте,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\).
\((x-2)^{5}=\left( \begin{array}{l}{5} \\ {0}\end{array}\right) x^{5}+\left( \begin{array}{c}{5} \\ {1}\end{array}\right) x^{4}(-2)+\left( \begin{array}{c}{5} \\ {2}\end{array}\right) x^{3}(-2)^{2}+\left( \begin{array}{c}{5} \\ {3}\end{array}\right) x^{2}(-2)^{3}+\left( \begin{array}{c}{5} \\ {4}\end{array}\right) x(-2)^{4}+\left( \begin{array}{c}{5} \\ {5}\end{array}\right)(-2)^{5}\)
\((x-2)^{5}=1 x^{5}+5(-2) x^{4}+\frac{5 !}{2 ! \cdot 3 !}(-2)^{2} x^{3}+\frac{5 !}{3 ! 2 !}(-2)^{3} x^{2}+\frac{5 !}{4 !1 !}(-2)^{4} x+1(-2)^{5}\)
\((x-2)^{5}=x^{5}+5(-2) x^{4}+10 \cdot 4 \cdot x^{3}+10(-8) x^{2}+5 \cdot 16 \cdot x+1(-32)\)
\((x-2)^{5}=x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32\)
Використовуйте Біноміальну теорему для розширення\((x-3)^{5}\).
- Відповідь
-
\(\begin{array}{l}{x^{5}-15 x^{4}+90 x^{3}-270 x^{2}} {+405 x-243}\end{array}\)
Використовуйте Біноміальну теорему для розширення\((y-1)^{6}\).
- Відповідь
-
\(\begin{array}{l}{y^{6}-6 y^{5}+15 y^{4}-20 y^{3}+15 y^{2}} {-6 y+1}\end{array}\)
Речі можуть стати брудними, коли обидва терміни мають коефіцієнт і змінну.
Використовуйте Біноміальну теорему для розширення\((2x-3y)^{4}\).
Рішення:
Визначаємо\(a\) і по\(b\) викрійці.
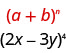
У нашій викрійці,\(a=2x\) і\(b=-3y\).
Використовуємо біноміальну теорему.
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
Підставляємо в значення\(a=2x, b=-3y\) і\(n=4\).
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{4-1}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{4-2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{4-3}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right) (-3y)^{4}\)
Спростіть показники.
\((2 x-3 y)^{4}=\left( \begin{array}{l}{4} \\ {0}\end{array}\right)(2 x)^{4}+\left( \begin{array}{c}{4} \\ {1}\end{array}\right)(2 x)^{3}(-3 y)^{1}+\left( \begin{array}{c}{4} \\ {2}\end{array}\right)(2 x)^{2}(-3 y)^{2}+\left( \begin{array}{c}{4} \\ {3}\end{array}\right)(2 x)^{1}(-3 y)^{3}+\left( \begin{array}{c}{4} \\ {4}\end{array}\right)(-3 y)^{4}\)
Оцініть коефіцієнти. Пам'ятайте,\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n, \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1, \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
\((2 x-3 y)^{4}=1(2 x)^{4}+4(2 x)^{3}(-3 y)^{1}+\frac{4 !}{2 !(2 x) !}(2 x)^{2}+\frac{4 !}{3 !(4-3) !}(2 x)^{3}(-3 y)^{3}+1(-3 y)^{4}\)
\((2 x-3 y)^{4}=16 x^{4}+4 \cdot 8 x^{3}(-3 y)+6\left(4 x^{2}\right)\left(9 y^{2}\right)+4(2 x)\left(-27 y^{3}\right)+81 y^{4}\)
\((2 x-3 y)^{4}=16 x^{4}-96 x^{3} y+216 x^{2} y^{2}-216 x y^{3}+81 y^{4}\)
Використовуйте Біноміальну теорему для розширення\((3x-2y)^{5}\).
- Відповідь
-
\(\begin{array}{l}{243 x^{5}-810 x^{4} y+1080 x^{3} y^{2}} {-720 x^{2} y^{3}+240 x y^{4}-32 y^{5}}\end{array}\)
Використовуйте Біноміальну теорему для розширення\((4x-3y)^{4}\).
- Відповідь
-
\(\begin{array}{l}{256 x^{4}-768 x^{3} y+864 x^{2} y^{2}} {-432 x y^{3}+81 y^{4}}\end{array}\)
Справжня краса біноміальної теореми полягає в тому, що вона дає формулу для будь-якого конкретного члена розширення без необхідності обчислювати всю суму. Давайте пошукаємо закономірність у біноміальної теоремі.
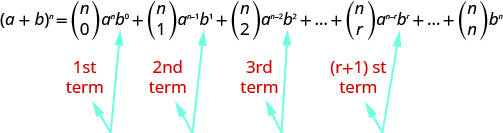
Зверніть увагу, що в кожному випадку\(b\) показник на одиницю менше, ніж число терміна. \((r+1)^{st}\)Термін - це термін, де показник\(b\) є\(r\). Таким чином, ми можемо використовувати формат\((r+1)^{st}\) терміна, щоб знайти значення конкретного терміна.
Знайдіть конкретний термін у біноміальному розширенні
\((r+1)^{s t}\)Термін в розширенні\((a+b)^{n}\) - це
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}\)
Знайдіть четвертий термін\((x+y)^{7}\).
Рішення:
| У нашій викрійці,\(n=7, a=x\) і\(b=y\). | 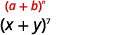 |
|
Шукаємо четвертий термін. З тих пір\(r+1=4\)\(r=3\). |
|
| Напишіть формулу | 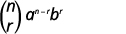 |
| Підставляємо в значення\(n=7, r=3, a=x\), і\(b=y\). | 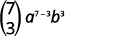 |
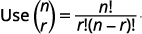 |
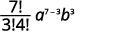 |
| Спростити. | 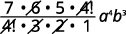 |
| Спростити. |  |
Знайдіть третій термін\((x+y)^{6}\).
- Відповідь
-
\(15x^{4}y^{2}\)
Знайдіть п'ятий термін\((a+b)^{8}\).
- Відповідь
-
\(8ab^{7}\)
Знайти коефіцієнт\(x^{6}\) терміну\((x+3)^{9}\).
Рішення:
| У нашій викрійці, то\(n=9, a=x\), і\(b=3\). |

|
| Шукаємо коефіцієнт\(x^{6}\) терміну. З тих пір\(a=x\), і\(x^{9-r}=x^{6}\), ми знаємо\(r=3\). | |
| Напишіть формулу. |
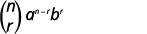
|
| Підставляємо в значення\(n=9, 4=3, a=x\), і\(b=3\). |
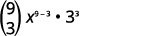
|
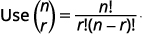
|
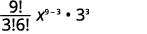
|
| Спростити. |
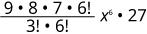
|
| Спростити. |
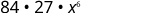
|
| Спростити. |

|
Знайти коефіцієнт\(x^{5}\) терміну\((x+4)^{8}\).
- Відповідь
-
\(7,168\)
Знайти коефіцієнт\(x^{4}\) терміну\((x+2)^{7}\).
- Відповідь
-
\(280\)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з послідовностями.
Ключові поняття
- Патерни в розширенні\ (a+b) ^ {n}\ (
- Кількість термінів - це\(n+1\).
- Перший термін -\(a^{n}\) і останній термін -\(b^{n}\).
- Показники на\(a\) зменшення на одиницю на кожен термін йде зліва направо.
- Показники\(b\) збільшення на одиницю на кожен термін йде зліва направо.
- Сума показників на будь-якому терміні дорівнює\(n\).
- Трикутник Паскаля

- Біноміальний коефіцієнт \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\): Біноміальний коефіцієнт\(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), де\(r\) і\(n\) є цілими числами з\(0≤r≤n\), визначається як
\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)
Читаємо\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) як «\(n\)вибрати\(r\)» або «\(n\)\(r\)взято за раз».
- Властивості біноміальних коефіцієнтів
\(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)=n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\end{array}\right)=1\)
- Біноміальна теорема:
Для будь-яких дійсних чисел\(a\)\(b\), і натуральних чисел\(n\),
\((a+b)^{n}=\left( \begin{array}{c}{n} \\ {0}\end{array}\right) a^{n}+\left( \begin{array}{c}{n} \\ {1}\end{array}\right) a^{n-1} b^{1}+\left( \begin{array}{c}{n} \\ {2}\end{array}\right) a^{n-2} b^{2}+\ldots+\left( \begin{array}{c}{n} \\ {r}\end{array}\right) a^{n-r} b^{r}+\ldots+\left( \begin{array}{c}{n} \\ {n}\end{array}\right) b^{n}\)
