Skip to main content
LibreTexts - Ukrayinska

12.2: Послідовності

  1. Last updated
  2. Save as PDF
  • Page ID
    59418

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Напишіть перші кілька термінів послідовності
    • Знайти формулу для загального члена (n-го члена) послідовності
    • Використовувати факторіальні позначення
    • Знайти часткову суму
    • Використовуйте позначення підсумовування, щоб записати суму

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Оцінити\(2n+3\) для цілих чисел\(1, 2, 3\), і\(4\).
      Якщо ви пропустили цю проблему, перегляньте приклад 1.6.
    2. Оцінити\((−1)^{n}\) для цілих чисел\(1, 2, 3\), і\(4\).
      Якщо ви пропустили цю проблему, перегляньте приклад 1.19.
    3. Якщо\(f(n)=n^{2}+2\), знайдіть\(f(1)+f(2)+f(3)\).
      Якщо ви пропустили цю проблему, перегляньте приклад 3.49.

    Напишіть перші кілька термінів послідовності

    Давайте подивимося на функцію\(f(x)=2x\) і оцінимо її лише для підрахунку чисел.

    \(f(x)=2x\)  
    \(x\) \(2x\)
    \(1\) \(2\)
    \(2\) \(4\)
    \(3\) \(6\)
    \(4\) \(8\)
    \(5\) \(10\)
    \(...\) \(...\)
    Таблиця 12.1.1

    Якщо ми перерахуємо значення функції в порядку як\(2, 4, 6, 8\), і\(10\),... у нас є послідовність. Послідовність - це функція, доменом якої є підрахунок чисел.

    Визначення\(\PageIndex{1}\)

    Послідовність - це функція, доменом якої є підрахунок чисел.

    Послідовність також може розглядатися як упорядкований список чисел, і кожне число у списку є терміном. Послідовність може мати нескінченну кількість членів або кінцеву кількість членів. Наша послідовність має три крапки (крапки) в кінці, що вказує на те, що список ніколи не закінчується. Якщо домен являє собою набір всіх рахункових чисел, то послідовність є нескінченною послідовністю. Його домен - це все підрахунок чисел і існує нескінченна кількість підрахунку чисел.

    \(2,4,6,8,10, \dots\)

    Якщо обмежити домен кінцевим числом підрахунку чисел, то послідовність є кінцевою послідовністю. Якщо ми використовуємо лише перші чотири числа підрахунку,\(1, 2, 3, 4\) наша послідовність буде кінцевою послідовністю,

    \(2,4,6,8\)

    Часто при роботі з послідовностями ми не хочемо виписувати всі терміни. Ми хочемо більш компактний спосіб показати, як визначається кожен термін. Коли ми працювали з функціями, ми писали,\(f(x)=2x\) і ми сказали, що вираз\(2x\) було правило, яке визначало значення в діапазоні. Хоча послідовність є функцією, ми не використовуємо звичні позначення функції. Замість того, щоб писати функцію як\(f(x)=2x\), ми б написали її як\(a_{n}=2n\). The\(a_{n}\) -\(n\) й член послідовності, термін у тій\(n\) позиції, де\(n\) - значення в області. Формула запису\(n\) -го члена послідовності називається загальним терміном або формулою послідовності.

    Визначення\(\PageIndex{2}\)

    Загальний термін послідовності знаходять з формули запису\(n\) го члена послідовності. Термін послідовності\(a_{n}\), - це термін у тій\(n\) позиції,\(n\) де значення в області.\(n\)

    Коли нам дається загальний термін послідовності, ми можемо знайти терміни, замінивши на\(n\) підрахунок чисел по порядку. Для\(a_{n}=2 n\),

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
    \(a_{n}\) 2\(\cdot 1\) 2\(\cdot 2\) 2\(\cdot 3\) 2\(\cdot 4\) 2\(\cdot 5\) 2\(\cdot 6\)
      \(2\) \(4\) \(6\) \(8\) \(10\)  
    Таблиця 12.1.2

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \ldots, \quad a_{n}, \dots\)

    \(2, \quad 4, \quad 6, \quad 8, \quad10, \dots\)

    Щоб знайти значення послідовності, підставляємо в підрахунку чисел по порядку в загальний член послідовності.

    Приклад\(\PageIndex{1}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=4 n-3\).

    Рішення:

    Підставляємо значення\(1, 2, 3, 4\), і\(5\) в формулу\(a_{n}=4n−3\), по порядку.

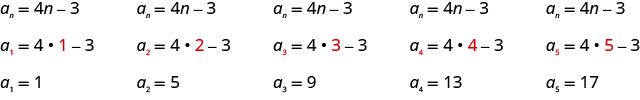
    На цьому малюнку показані три рядки і п'ять стовпців. Перший рядок читає n-й член дорівнює 4 рази n мінус 3 написано п'ять разів. Другий рядок читає суб 1 дорівнює 4 рази г раз 1 мінус 3, суб 2 дорівнює 4 рази г раз 2 мінус 3, суб 3 дорівнює 4 рази г раз 3 мінус 3, суб 4 дорівнює 4 раз г раз 4 мінус 3, суб 5 дорівнює 4 рази г раз 5 мінус 3. Третій рядок читає, суб 1 дорівнює 1, суб 2 дорівнює 5, суб 3 дорівнює 9, суб 4 дорівнює 13, суб 5 дорівнює 17.
    Малюнок 12.1.1

    Відповідь:

    Перші п'ять членів послідовності є\(1, 5, 9, 13\), і\(17\).

    Вправа\(\PageIndex{1}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=3n-4\).

    Відповідь

    \(-1,2,5,8,11\)

    Вправа\(\PageIndex{2}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=2n-5\).

    Відповідь

    \(-3,-1,1,3,5\)

    Для деяких послідовностей змінна є експонентою.

    Приклад\(\PageIndex{2}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=2^{n}+1\).

    Рішення:

    Підставляємо значення\(1, 2, 3, 4\), і\(5\) в формулу\(a_{n}=2^{n}+1\), по порядку.

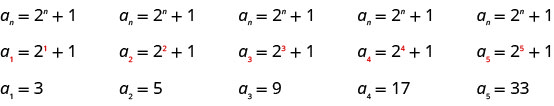
    На цьому малюнку показані три рядки і п'ять стовпців. Перший рядок читає «n-й член дорівнює 2 до n-ї потужності плюс 1» написано п'ять разів. Другий рядок читає, «суб 1 дорівнює 2 рази 1 плюс 1, суб 2 дорівнює 2 до потужності 2 плюс 1, суб 3 дорівнює 2 до потужності 3 плюс 1, суб 4 дорівнює 2 до потужності 4 плюс 1, суб 5 дорівнює 2 до потужності 5 плюс 1». Останній рядок читає «суб 1 дорівнює 3, суб 2 дорівнює 5, суб 3 дорівнює 9, суб 4 дорівнює 17, суб 5 дорівнює 33».
    Малюнок 12.1.2

    Відповідь:

    Перші п'ять членів послідовності є\(3, 5, 9, 17\), і\(33\).

    Вправа\(\PageIndex{3}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=3^{n}+4\).

    Відповідь

    \(7,13,31,85,247\)

    Вправа\(\PageIndex{4}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=2^{n}-5\).

    Відповідь

    \(-3,-1,3,11,27\)

    Не рідкість бачити вирази\((−1)^{n}\) або\((−1)^{n+1}\) в загальному терміні для послідовності. Якщо ми оцінюємо кожне з цих виразів за кілька значень, то побачимо, що цей вираз чергує знак для термінів.

    \(n\) \(1\) \(2\) \(3\) \(4\) \(5\)
    \ (n\) ">\((-1)^{n}\) \ (1\) ">\((-1)^{1}\)
    \(-1\)    		 \ (2\) ">\((-1)^{2}\)
    1    		 \ (3\) ">\((-1)^{3}\)
    \(-1\)    		 \ (4\) ">\((-1)^{4}\)
    \(1\)    		 \ (5\) ">\((-1)^{5}\)
    \(-1\)
    \ (n\) ">\((-1)^{n+1}\) \ (1\) ">\((-1)^{1+1}\)
    1    		 \ (2\) ">\((-1)^{2+1}\)
    \(-1\)    		 \ (3\) ">\((-1)^{3+1}\)
    1    		 \ (4\) ">\((-1)^{4+1}\)
    \(-1\)    		 \ (5\) ">\((-1)^{5+1}\)
    1
    Таблиця 12.1.3

    \(a_{1}, \quad a_{2}, \quad a_{3}, \quad a_{4}, \quad a_{5}, \dots, \quad a_{n}, \dots\)

    \(\begin{array}{rrrr}{-1,} & {1,} & {-1,} & {1,} & {-1 \ldots} \\ {1,} & {-1,} & {1,} & {-1,} & {1 \ldots}\end{array}\)

    Приклад\(\PageIndex{3}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=(-1)^{n} n^{3}\).

    Рішення:

    Підставляємо значення\(1, 2, 3, 4\), і\(5\) в формулу\(a_{n}=(-1)^{n} n^{3}\), по порядку.

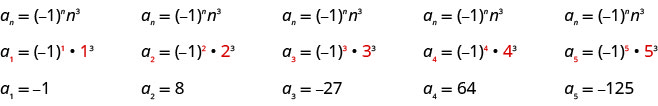
    На цьому малюнку показані три рядки і п'ять стовпців. У першому рядку написано «n-й член дорівнює від'ємному 1 до n-ї потужності раз n кубічний», написаний п'ять разів. Другий рядок читає суб 1 дорівнює негативний 1 до потужності 1 раз г раз 1 куб, суб 2 дорівнює негативний 1 в квадраті часу г раз 2 куб, суб 3 дорівнює негативний 1 в кубі раз г раз 23 в кубі, суб 4 дорівнює негативний 1 до потужності 4 раз г разів 4 куб, суб 5 дорівнює негативний 1 до потужності 5 3 г раз 5 куб. Останній рядок читає, «суб 1 дорівнює негативний 1, суб 2 дорівнює 8, суб 3 дорівнює негативний 27, суб 4 дорівнює 64, а суб 5 дорівнює негативним 125.
    Малюнок 12.1.3

    Відповідь:

    Перші п'ять членів послідовності є\(−1, 8, −27, 64, −1, 8, −27, 64\), і\(−125\).

    Вправа\(\PageIndex{5}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=(-1)^{n} n^{2}\).

    Відповідь

    \(-1,4,-9,16,-25\)

    Вправа\(\PageIndex{6}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=(-1)^{n+1} n^{3}\).

    Відповідь

    \(1,-8,27,-64,125\)

    Знайти формулу для загального члена (\(n\)го члена) послідовності

    Іноді у нас є кілька термінів послідовності, і було б корисно знати загальний термін або\(n\) термін. Щоб знайти загальний термін, шукаємо закономірності в термінами. Часто шаблони включають кратні або повноваження. Також шукаємо закономірність в знаках термінів.

    Приклад\(\PageIndex{4}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані. \(4,8,12,16,20, \dots\)

    Рішення:


      .
      .
    Шукаємо викрійку в терміни. .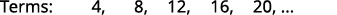
    Числа є кратними\(4\). .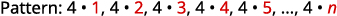
      Загальним терміном послідовності є\(a_{n}=4n\).
    Таблиця 12.1.4

    Відповідь:

    Загальним терміном послідовності є\(a_{n}=4n\).

    Вправа\(\PageIndex{7}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані.

    \(3,6,9,12,15, \dots\)

    Відповідь

    \(a_{n}=3 n\)

    Вправа\(\PageIndex{8}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані.

    \(5,10,15,20,25, \dots\)

    Відповідь

    \(a_{n}=5 n\)

    Приклад\(\PageIndex{5}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані. \(2,-4,8,-16,32, \dots\)

    Рішення:

     
    .
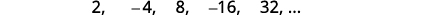
    Малюнок 12.1.8
     
    .
    Малюнок 12.1.9
    Шукаємо викрійку в терміни.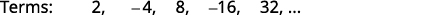
    .
    Малюнок 12.1.10
    Цифри - це повноваження\(2\). Прикмети чергуються, з навіть\(n\) негативними.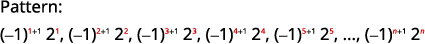
    .
    Малюнок 12.1.11
      Загальний термін послідовності\(a_{n}=(-1)^{n+1} 2^{n}\)
    Таблиця 12.1.5

    Відповідь:

    Загальним терміном послідовності є\(a_{n}=(-1)^{n+1}2^{n}\).

    Вправа\(\PageIndex{9}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані.

    \(-3,9,-27,81,-243, \dots\)

    Відповідь

    \(a_{n}=(-1)^{n} 3^{n}\)

    Вправа\(\PageIndex{10}\)

    Знайти загальний термін для послідовності, перші п'ять членів якої показані

    \(1,-4,9,-16,25, \dots\)

    Відповідь

    \(a_{n}=(-1)^{n+1} n^{2}\)

    Приклад\(\PageIndex{6}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані. \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \dots\)

    Рішення:

     
    .
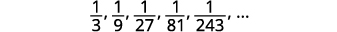
    Малюнок 12.1.12
     
    .
    Малюнок 12.1.13
    Шукаємо викрійку в терміни.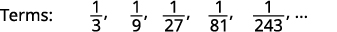
    .
    Малюнок 12.1.14
    Чисельники - це все\(1\).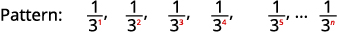
    .
    Малюнок 12.1.15
    Знаменниками є повноваження\(3\). Загальним терміном послідовності є\(a_{n}=\frac{1}{3^{n}}\).
    Таблиця 12.1.6

    Відповідь:

    Загальним терміном послідовності є\(a_{n}=\frac{1}{3^{n}}\).

    Вправа\(\PageIndex{11}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані.

    \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \dots\)

    Відповідь

    \(a_{n}=\frac{1}{2^{n}}\)

    Вправа\(\PageIndex{12}\)

    Знайдіть загальний термін для послідовності, перші п'ять членів якої показані.

    \(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \dots\)

    Відповідь

    \(a_{n}=\frac{1}{n^{2}}\)

    Використовувати факторіальні позначення

    Послідовності часто мають терміни, які є добутком послідовних цілих чисел. Ми вказуємо ці вироби спеціальним позначенням, званим факторіальними позначеннями. Наприклад\(5!\), читати\(5\) факторіал, значить\(5⋅4⋅3⋅2⋅1\). Знак оклику тут не є розділовим знаком; він вказує на факторіальні позначення.

    Визначення\(\PageIndex{3}\)

    Якщо\(n\) є натуральним числом,\(n!\) то

    \(n !=n(n-1)(n-2) \dots\)

    Визначаємо\(0!\) як\(1\), так\(0!=1\).

    Показані значення\(n!\) для перших\(5\) натуральних чисел.

    \(\begin{array}{ccccc}{1 !} & {2 !} & {3 !} & {4 !} & {5 !} \\ {1} & \quad{2 \cdot 1} & \quad {3 \cdot 2 \cdot 1} & \quad{4 \cdot 3 \cdot 2 \cdot 1} & \quad {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ {1} & {2} & {6} & {24} & {120}\end{array}\)

    Приклад\(\PageIndex{7}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=\frac{1}{n !}\).

    Рішення:

    Підставляємо значення\(1, 2, 3, 4, 5\) в формулу\(a_{n}=\frac{1}{n !}\), по порядку.

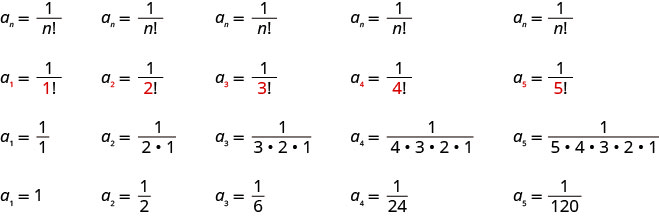
    На цьому малюнку показані чотири рядки і п'ять стовпців. Перший рядок говорить: «n-й член дорівнює одиниці, поділеної на n факторіал» написано п'ять разів. Другий рядок читає «суб 1 дорівнює один ділиться на 1 факторіал, суб 2 дорівнює 1 ділиться на 2 факторіал, суб 3 дорівнює 1 ділиться на 3 факторіал, суб 4 дорівнює 1 ділиться на 4 факторіал, суб 5 дорівнює 1 ділиться на 5 факторіал». Третій рядок читає «суб 1 дорівнює 1 розділений 1», «суб 2 дорівнює 1 ділиться на 2 рази г раз 1», «суб 3 дорівнює 1 ділиться на 3 рази г раз 2 г раз 1», «суб 4 дорівнює 1 розділений 4 рази г раз 3 рази г раз 2 рази раз 1», «суб 5 дорівнює 1 ділиться на 5 г раз 4 рази г разів 3 рази г раз 2 рази г раз 1», «суб 1 дорівнює 1, суб 2 дорівнює одній половині», «суб 3 дорівнює одній шостій», «суб 4 дорівнює 1 ділиться на 24», «суб 5 дорівнює 1 ділиться на 120».
    Малюнок 12.1.16

    Відповідь:

    Перші п'ять членів послідовності є\(1, \frac{1}{2}, \frac{1}{6}, \frac{1}{24}, \frac{1}{120}\).

    Вправа\(\PageIndex{13}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=\frac{2}{n !}\).

    Відповідь

    \(2,1, \frac{1}{3}, \frac{1}{12}, \frac{1}{60}\)

    Вправа\(\PageIndex{14}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=\frac{3}{n !}\).

    Відповідь

    \(3, \frac{3}{2}, \frac{1}{2}, \frac{1}{8}, \frac{1}{40}\)

    Коли в чисельнику та знаменнику є дріб з факторіалами, ми вирівнюємо коефіцієнти вертикально, щоб полегшити наші розрахунки.

    Приклад\(\PageIndex{8}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=\frac{(n+1) !}{(n-1) !}\).

    Рішення:

    Підставляємо значення\(1, 2, 3, 4, 5\) в формулу\(a_{n}=\frac{(n+1) !}{(n-1) !}\), по порядку.

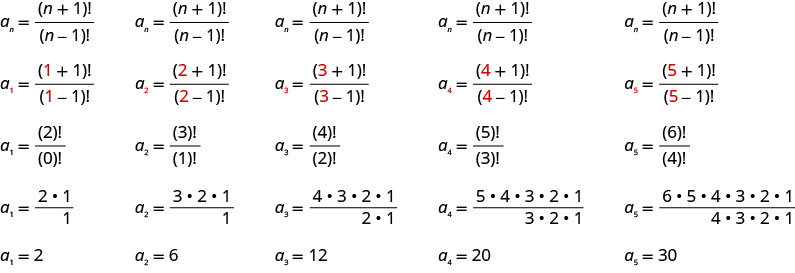
    На цьому малюнку показані п'ять стовпців і п'ять рядків. Перший рядок показує послідовність «n-й член дорівнює n плюс 1 раз факторіал ділиться на n мінус 1 раз факторіал» написана п'ять разів. Другий рядок «суб 1 дорівнює 1 плюс 1 раз факторіал ділиться на 1 мінус 1 раз факторіал», «суб 2 дорівнює 2 плюс 1 раз факторіал ділиться на 2 мінус 1 раз факторіал», «суб 3 дорівнює 3 плюс 1 раз факторіал розділений на 3 мінус 1 раз факторіал», «суб 4 дорівнює 4 плюс 1 раз факторіал розділений на 4 мінус 1 раз факторіал», «суб 5 дорівнює 5 плюс 1 раз факторіал ділиться на 5 мінус 1 раз факторіал». Третій рядок читає «суб 1 дорівнює 2 рази факторіал розділений на 0 раз факторіал», «суб 2 дорівнює 3 рази факторіал розділений на 1 раз факторіал», «суб 3 дорівнює 4 рази факторіал розділений на 2 рази факторіал», «суб 3 дорівнює 4 рази факторіал розділений на 2 рази факторіал», «суб 4 дорівнює 5 раз факторіала розділений на 3 рази факторіал», «суб 5 дорівнює 6 разів факторіал розділений на 4 рази факторіал». Четвертий ряд читає, «суб 1 дорівнює 2 рази г часу 1 ділиться на 1», «суб 2 дорівнює 3 рази г раз 2 рази г раз 1 ділиться на 1», «суб 3 дорівнює 4 рази г раз 3 рази г раз 2 рази г раз 1 ділиться на 2 рази г раз 1», «суб 4 дорівнює 5 раз г разів 4 рази г разів 3 рази г раз 2 рази г раз 1 розділений на 3 г раз 2 рази г раз 1», і «суб 5 дорівнює 6 разів г раз 5 раз г раз 4 рази г раз 3 рази г раз 2 рази г раз 2 рази г раз 1 ділиться на 4 рази г раз 3 рази г раз 2 рази г раз 1». П'ятий рядок читає «суб 1 дорівнює 2», «суб 2 дорівнює 6», «суб 3 дорівнює 12», «суб 4 дорівнює 20», «суб 5 дорівнює 30».
    Малюнок 12.1.17

    Відповідь:

    Перші п'ять членів послідовності є\(2, 6, 12, 20\), і\(30\).

    Вправа\(\PageIndex{15}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої\(a_{n}=\frac{(n-1) !}{(n+1) !}\)

    Відповідь

    \(\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}, \frac{1}{30}\)

    Вправа\(\PageIndex{16}\)

    Напишіть перші п'ять членів послідовності, загальний термін якої дорівнює\(a_{n}=\frac{n !}{(n+1) !}\).

    Відповідь

    \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\)

    Знайти часткову суму

    Іноді в додатках, а не просто перераховувати терміни, нам важливо додати терміни послідовності. Замість того, щоб просто з'єднувати терміни зі знаками плюс, ми можемо використовувати підсумовувальні позначення.

    Наприклад,\(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\) може бути написано як\(\sum_{i=1}^{5} a_{i}\). Ми читаємо це як «сума\(a\) суб\(i\) від\(i\) дорівнює один до п'яти». Символ\(∑\) означає додати і індекс\(i\) підсумовування. The\(1\) говорить нам, з чого почати (початкове значення), а потім\(5\) говорить нам, де закінчити (термінальне значення).

    Визначення\(\PageIndex{4}\)

    Сума перших\(n\) членів послідовності, чий\(n\) член\(a_{n}\) записується в підсумовувальному позначенні як:

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    The\(i\) є індекс підсумовування, і він\(1\) говорить нам, з чого почати, а потім\(n\) говорить нам, де закінчити.

    Коли ми додаємо кінцеве число членів, ми називаємо суму частковою сумою.

    Приклад\(\PageIndex{9}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{i=1}^{5} 2 i\).

    Рішення:

      \(\sum_{i=1}^{5} 2 i\)
    Підставляємо значення\(1, 2, 3, 4, 5\) по порядку. \(2 \cdot 1+2 \cdot 2+2 \cdot 3+2 \cdot 4 + 2 \cdot 5\)
    Спростити. \(2+4+6+8+10\)
    Додати. \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Таблиця 12.1.7

    Відповідь:

    \(\begin{array} {c} 30\\ \sum_{i=1}^{5} 2 i=30 \end{array}\)
    Вправа\(\PageIndex{17}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{i=1}^{5} 3 i\).

    Відповідь

    \(45\)

    Вправа\(\PageIndex{18}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{i=1}^{5} 4 i\).

    Відповідь

    \(60\)

    Індекс не завжди повинен бути,\(i\) ми можемо використовувати будь-яку букву, але\(i\) і зазвичай\(k\) використовуються. Індекс не повинен починатися ні з одного\(1\) - він може починатися і закінчуватися будь-яким додатним цілим числом.

    Приклад\(\PageIndex{10}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{k=0}^{3} \frac{1}{k !}\).

    Рішення:

    \(\begin{array}{c c} {}&{\sum_{k=0}^{3} \frac{1}{k !}} \\ {We\:substitute\:the\:values\:0,1,2,3\:in\:order.}&{\frac{1}{1}+\frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}} \\ {Evaluate\:the\:factorials.}& {\frac{1}{1}+\frac{1}{1}+\frac{1}{2 !}+\frac{1}{6}} \\ {Simplify.}&{1+1+\frac{3}{6}+\frac{1}{6}} \\{Simplify.}& {\frac{16}{6}} \\ {Simplify.}&{\frac{8}{3}} \\{}& {\sum_{k=0}^{3} \frac{1}{k !}=\frac{8}{3}}\end{array}\)

    Вправа\(\PageIndex{19}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{k=0}^{3} \frac{2}{k !}\).

    Відповідь

    \(\frac{16}{3}\)

    Вправа\(\PageIndex{20}\)

    Розгорніть часткову суму і знайдіть її значення:\(\sum_{k=0}^{3} \frac{3}{k !}\).

    Відповідь

    \(8\)

    Використовуйте позначення підсумовування для написання суми

    В останніх двох прикладах ми перейшли від підсумовувальних позначень до виписування суми. Тепер почнемо з суми і змінимо її на підсумовувальні позначення. Це дуже схоже на знаходження загального терміну послідовності. Нам потрібно буде подивитися терміни і знайти закономірність. Часто шаблони включають кратні або повноваження.

    Приклад\(\PageIndex{11}\)

    Запишіть суму, використовуючи підсумовувальні позначення:\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\).

    Рішення:

    \(\begin{array} {}&{ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}} \\ {}&{n : 1,2,3,4,5} \\ {\text{We look for a pattern in the terms.}}&{\text { Terms: } 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}} \\ {\text{The numerators are all one.}}&{\text { Pattern: } \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots \frac{1}{n}} \\ {\text{The denominators are the counting numbers from one to five.}}&{\text{The sum written in summation notation}} \\ {}&{1 + \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\sum^{5}_{n=1} \frac{1}{n}.} \end{array}\)

    Вправа\(\PageIndex{21}\)

    Запишіть суму, використовуючи підсумовувальні позначення:\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\).

    Відповідь

    \(\sum_{n=1}^{5} \frac{1}{2^{n}}\)

    Вправа\(\PageIndex{22}\)

    Запишіть суму, використовуючи підсумовувальні позначення:\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}\)

    Відповідь

    \(\sum_{n=1}^{5} \frac{1}{n^{2}}\)

    Коли члени суми мають негативні коефіцієнти, треба уважно проаналізувати закономірність знаків.

    Приклад\(\PageIndex{12}\)

    Запишіть суму, використовуючи підсумовувальні позначення:\(-1+8-27+64-125\).

    Рішення:


     
    .
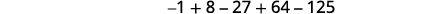
    Малюнок 12.1.18
     
    .
    Малюнок 12.1.19
    Шукаємо викрійку в терміни.
    .
    Малюнок 12.1.20
    Знаки термінів чергуються,
    а непарні - негативні.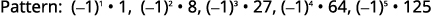
    .
    Малюнок 12.1.21
    Цифри - це куби
    рахункових чисел від одного до п'яти.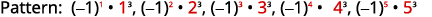
    .
    Малюнок 12.1.22
     
    .
    Малюнок 12.1.23
      Сума, записана в підсумовувальних позначеннях
      \(-1+8-27+64-125=\sum_{n=1}^{5}(-1)^{n} \cdot n^{3}\)
    Таблиця 12.1.8
    Вправа\(\PageIndex{23}\)

    Запишіть кожну суму, використовуючи підсумовувальні позначення:\(1-4+9-16+25\).

    Відповідь

    \(\sum_{n=1}^{5}(-1)^{n+1} n^{2}\)

    Вправа\(\PageIndex{24}\)

    Запишіть кожну суму, використовуючи підсумовувальні позначення:\(-2+4-6+8-10\).

    Відповідь

    \(\sum_{n=1}^{5}(-1)^{n} 2 n\)

    Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з послідовностями.

    https://openstax.org/l/37serseqfindpat

    Ключові концепції

    • Факторіальні позначення

    Якщо\(n\) є натуральним числом,\(n!\) то

    \(n !=n(n-1)(n-2) \ldots(3)(2)(1)\)

    Визначаємо\(0!\) як\(1\), так\(0!=1\)

    • Позначення підсумовування

    Сума перших\(n\) членів послідовності,\(n\) -й член якої\(a_{n}\) записується в підсумовувальному позначенні, як:

    \(\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+\ldots+a_{n}\)

    The\(i\) є індекс підсумовування, і він\(1\) говорить нам, з чого почати, а потім\(n\) говорить нам, де закінчити.

    Глосарій

    скінченна послідовність
    Послідовність з доменом, яка обмежена кінцевим числом підрахунку чисел.
    загальний термін послідовності
    Загальним терміном послідовності є формула для запису\(n\) го члена послідовності. Термін послідовності\(a_{n}\), - це термін у тій\(n\) позиції,\(n\) де значення в області.\(n\)
    нескінченна послідовність
    Послідовність, домен якої - це все підрахунок чисел і існує нескінченна кількість підрахунку чисел.
    часткова сума
    Коли ми додаємо скінченне число членів послідовності, ми називаємо суму частковою сумою.
    послідовність
    Послідовність - це функція, доменом якої є підрахунок чисел.