12.3: Арифметичні послідовності
- Page ID
- 59433
До кінця цього розділу ви зможете:
- Визначте, чи є послідовність арифметичною
- Знайти загальний термін (\(n\)й член) арифметичної послідовності
- Знайти суму перших\(n\) членів арифметичної послідовності
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Оцінити\(4n−1\) для цілих чисел\(1, 2, 3\), і\(4\).
Якщо ви пропустили цю проблему, перегляньте приклад 1.6. - Розв'яжіть систему рівнянь:\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
Якщо ви пропустили цю проблему, перегляньте приклад 4.9. - Якщо\(f(n)=\frac{n}{2}(3 n+5)\), знайдіть\(f(1)+f(20)\).
Якщо ви пропустили цю проблему, перегляньте приклад 3.49.
Визначте, чи є послідовність арифметичною
Останній розділ ввів послідовності, і тепер ми розглянемо два конкретних типи послідовностей, кожен з яких має особливі властивості. У цьому розділі ми розглянемо арифметичні послідовності, а в наступному розділі - геометричні послідовності.
Арифметична послідовність - це послідовність, де різниця між послідовними долями є постійною. Різниця між послідовними долями в арифметичній послідовності, a_ {n} -a_ {n-1}\(d\), є загальною різницею, для\(n\) більшої або рівної двом.
Арифметична послідовність - це послідовність, де різниця між послідовними термінами завжди однакова.
Різниця між послідовними термінами, a_ {n} -a_ {n-1}\(d\), є загальною різницею, для\(n\) більшої або рівної двом.
Визначте, чи є кожна послідовність арифметичною. Якщо так, вкажіть загальну різницю.
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
Рішення:
Щоб визначити, чи є послідовність арифметичною, знаходимо різницю показаних послідовних членів.
а.\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
Послідовність арифметична. Загальна відмінність полягає в тому\(d=4\).
б.\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
Послідовність не є арифметичною, оскільки всі відмінності між послідовними термінами не однакові. Загальної різниці немає.
c.\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
Відповідь:
Послідовність арифметична. Загальна відмінність полягає в тому\(d=-7\).
Визначте, чи є кожна послідовність арифметичною. Якщо так, вкажіть загальну різницю.
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- Відповідь
-
- Послідовність арифметична із загальною різницею\(d=11\).
- Послідовність арифметична із загальною різницею\(d=-6\).
- Послідовність не є арифметичною, оскільки всі відмінності між послідовними термінами не однакові.
Визначте, чи є кожна послідовність арифметичною. Якщо так, вкажіть загальну різницю.
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- Відповідь
-
- Послідовність не є арифметичною, оскільки всі відмінності між послідовними термінами не однакові.
- Послідовність арифметична із загальною різницею\(d=2\).
- Послідовність арифметична із загальною різницею\(d=−5\).
Якщо ми знаємо перший член\(a_{1}\), і загальна різниця\(d\), ми можемо перерахувати кінцеве число членів послідовності.
Напишіть перші п'ять членів послідовності, де перший член\(5\) і загальна різниця\(d=−6\).
Рішення:
Починаємо з першого члена і додаємо загальну різницю. Потім ми додаємо загальну різницю до цього результату, щоб отримати наступний термін, і так далі.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
Відповідь:
Послідовність така\(5,-1,-7,-13,-19, \dots\)
Напишіть перші п'ять членів послідовності, де перший член\(7\) і загальна різниця\(d=−4\).
- Відповідь
-
\(7,3,-1,-5,-9, \dots\)
Напишіть перші п'ять членів послідовності, де перший член\(11\) і загальна різниця\(d=−8\).
- Відповідь
-
\(11,3,-5,-13,-21, \dots\)
Знайти загальний термін (\(n\)й член) арифметичної послідовності
Так само, як ми знайшли формулу для загального члена послідовності, ми також можемо знайти формулу для загального члена арифметичної послідовності.
Давайте напишемо перші кілька членів послідовності, де перший член є\(a_{1}\) і загальна відмінність\(d\). Потім будемо шукати викрійку.
Коли ми шукаємо шаблон, ми бачимо, що кожен термін починається з\(a_{1}\).
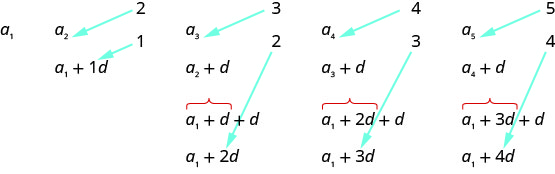
Перший термін додає\(0d\) до\(a_{1}\), другий термін додає\(1d\), третій додає\(2d\), четвертий термін додає\(3d\), а п'ятий термін додає\(4d\). Число\(ds\), до якого було додано\(a_{1}\), на одиницю менше, ніж число терміна. Це призводить нас до наступного
\(a_{n}=a_{1}+(n-1) d\)
Загальний термін арифметичної послідовності з першим\(a_{1}\) семеном і\(d\) спільною різницею
\(a_{n}=a_{1}+(n-1) d\)
Ми будемо використовувати цю формулу в наступному прикладі, щоб знайти 15-й член послідовності.
Знайдіть п'ятнадцятий член послідовності, де перший член є\(3\) і загальна різниця є\(6\).
Рішення:
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
Знайдіть двадцять сьомий член послідовності, де перший член є\(7\) і загальна різниця\(9\).
- Відповідь
-
\(241\)
Знайдіть вісімнадцятий член послідовності, де перший член є\(13\) і загальна різниця є\(−7\).
- Відповідь
-
\(-106\)
Іноді ми не знаємо першого терміну, і ми повинні використовувати іншу інформацію, щоб знайти її, перш ніж знайти запитуваний термін.
Знайдіть дванадцятий член послідовності, де сьомий член є\(10\) і загальна різниця\(−2\). Дайте формулу для загального терміну.
Рішення:
Щоб спочатку знайти перший член\(a_{1}\), використовуйте формулу з\(a_{7}=10\)\(n=7\), і\(d=−2\). Підставляємо в значення. Спростити.
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
Знайдіть дванадцятий член\(a_{12}\), використовуючи формулу з\(a_{1}=22\)\(n=12\), і\(d=-2\). Підставляємо в значення. Спростити.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
Дванадцятий член послідовності\(0, a_{12}=0\)
Щоб знайти загальний термін, підставляємо значення в формулу.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
Відповідь:
Загальний термін\(a_{n}=-2 n+24\)
Знайдіть одинадцятий член послідовності, де дев'ятий член є\(8\) і загальна різниця\(−3\). Дайте формулу для загального терміну.
- Відповідь
-
\(a_{11}=2 .\)Загальним терміном є\(a_{n}=-3 n+35\)
Знайдіть дев'ятнадцятий член послідовності, де п'ятий член\(1\) і загальна різниця\(−4\) є.Дайте формулу для загального члена.
- Відповідь
-
\(a_{19}=-55 .\)Загальним терміном є\(a_{n}=-4 n+21\)
Іноді надана інформація призводить нас до двох рівнянь у двох невідомих. Потім ми використовуємо наші методи для розв'язання систем рівнянь, щоб знайти необхідні значення.
Знайдіть перший член і загальну різницю послідовності, де п'ятий член\(19\) і одинадцятий член -\(37\). Дайте формулу для загального терміну.
Рішення:
Оскільки ми знаємо два терміни, ми можемо скласти систему рівнянь, використовуючи формулу для загального члена.
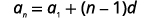 |
|
| Знаємо значення\(a_{5}\) і\(a_{11}\), тому будемо використовувати\(n=5\) і\(n=11\). | 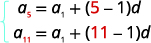 |
Підставляємо в значення,\(a_{5}=19\) і\(a_{11}=37\). |
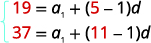 |
| Спростити. | 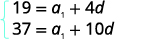 |
| Підготуйтеся усунути\(a_{1}\) термін, помноживши верхнє рівняння на\(−1\). Додайте рівняння. |
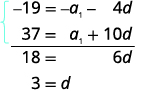 |
| Підставляємо\(d=3\) назад в перше рівняння. | 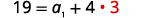 |
| Вирішити для\(a_{1}\). |  |
| Використовуйте формулу з\(a_{1}=7\) і\(d=3\). | 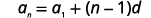 |
| Підставляємо в значення. | 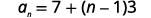 |
| Спростити. | 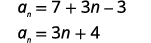 |
| Перший термін - це\(a_{1}=7\). Загальна відмінність полягає в тому\(d=3\). |
|
| Загальним терміном послідовності є\(a_{n}=3n+4\). |
Відповідь:
Загальним терміном послідовності є\(a_{n}=3n+4\).
Знайдіть перший член та загальну різницю послідовності, де четвертий член,\(17\) а тринадцятий -\(53\). Дайте формулу для загального терміну.
- Відповідь
-
\(a_{1}=5, d=4 .\)Загальний термін є\(a_{n}=4 n+1\).
Знайдіть перший член і загальну різницю послідовності, де третій член,\(2\) а дванадцятий член -\(−25\). Дайте формулу для загального терміну.
- Відповідь
-
\(a_{1}=8, d=-3 .\)Загальний термін є\(a_{n}=-3 n+11\).
Знайти суму перших\(n\) членів арифметичної послідовності
Як і у випадку з загальними послідовностями, часто корисно знайти суму арифметичної послідовності. Сума\(S_{n}\) перших\(n\) членів будь-якої арифметичної послідовності записується як\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\). Знайти суму, просто додаючи всі терміни, може бути нудно. Таким чином, ми також можемо розробити формулу, щоб знайти суму послідовності, використовуючи перший і останній член послідовності.
Ми можемо розробити цю нову формулу, спочатку написавши суму, починаючи з першого члена\(a_{1}\), і продовжуємо додавати a,\(d\) щоб отримати наступний член як:
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).
Ми також можемо змінити порядок термінів і написати суму, починаючи з\(a_{n}\) і продовжуючи віднімати,\(d\) щоб отримати наступний термін як
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).
Якщо додати ці два вирази для суми перших\(n\) членів арифметичної послідовності, то можна вивести формулу для суми перших\(n\) членів будь-якого арифметичного ряду.
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
Оскільки є\(n\) суми\((a_{1}+a_{n})\) на правій стороні рівняння, ми переписуємо правий бік як\(n(a_{1}+a_{n})\).
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
Ділимо на два, щоб вирішити для\(S_{n}\).
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Це дає нам загальну формулу для суми перших\(n\) членів арифметичної послідовності.
Сума\(S_{n}\) перших\(n\) членів арифметичної послідовності дорівнює
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
\(a_{1}\)де перший термін і\(a_{n}\)\(n\) -й термін.
Ми застосовуємо цю формулу в наступному прикладі, де наведені перші кілька членів послідовності.
Знайдіть суму перших\(30\) членів арифметичної послідовності:\(8, 13, 18, 23, 28, …\)
Рішення:
Щоб знайти суму, скористаємося формулою\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Ми знаємо\(a_{1}=8, d=5\) і\(n=30\), але нам потрібно знайти для\(a_{n}\) того, щоб використовувати формулу суми.
Знайти\(a_{n}\) де\(a_{1}=8, d=5\) і\(n=30\). Спростити.
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
Знаючи\(a_{1}=8, n=30\), і\(a_{30}=153\), використовуйте формулу суми. Підставляємо в значення. Спростити. Спростити.
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
Знайдіть суму перших\(30\) членів арифметичної послідовності:\(5, 9, 13, 17, 21, …\)
- Відповідь
-
\(1,890\)
Знайдіть суму перших\(30\) членів арифметичної послідовності:\(7, 10, 13, 16, 19, …\)
- Відповідь
-
\(1,515\)
У наступному прикладі нам дано загальний термін для послідовності і пропонується знайти суму перших\(50\) членів.
Знайти суму перших\(50\) членів арифметичної послідовності, загальний член якої дорівнює\(a_{n}=3n−4\).
Рішення:
Щоб знайти суму, скористаємося формулою\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Ми знаємо\(n=50\), але нам потрібно знайти\(a_{1}\) і для\(a_{n}\) того, щоб використовувати формулу суми.
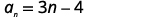 |
|
| Знайти\(a_{1}\), підставивши\(n=1\). | 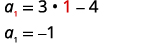 |
| Знайти\(a_{n}\) шляхом підстановки\(n=50\). | 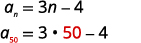 |
| Спростити. | 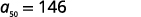 |
| Знаючи\(n=50, a_{1}=−1,\) і\(a_{50}=146\) використовуйте формулу суми. | 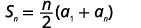 |
| Підставляємо в значення. | 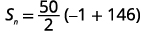 |
| Спростити. | 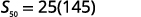 |
| Спростити. | 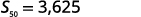 |
Знайти суму перших\(50\) членів арифметичної послідовності, загальний член якої дорівнює\(a_{n}=2n−5\).
- Відповідь
-
\(2,300\)
Знайти суму перших\(50\) членів арифметичної послідовності, загальний член якої дорівнює\(a_{n}=4n+3\).
- Відповідь
-
\(5,250\)
У наступному прикладі ми наводимо суму в підсумовувальних позначеннях. Додавати всі терміни було б нудно, тому ми витягуємо інформацію, необхідну для використання формули, щоб знайти суму перших\(n\) членів.
Знайдіть суму:\(\sum_{i=1}^{25}(4 i+7)\).
Рішення:
Щоб знайти суму, скористаємося формулою\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Ми знаємо\(n=25\), але нам потрібно знайти\(a_{1}\) і для\(a_{n}\) того, щоб використовувати формулу суми.
| Розгорніть позначення підсумовування. |
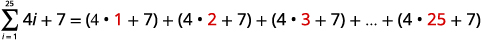
|
| Спростити. |
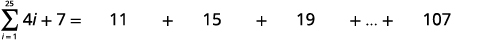
|
| Ідентифікувати\(a_{1}\). |  |
| Ідентифікувати\(a_{25}\). |

|
| Знаючи\(n=25, a_{1}=11\), і\(a_{25} = 107\) використовуйте формулу суми. |  |
| Підставляємо в значення. |  |
| Спростити. |  |
| Спростити. |  |
Знайдіть суму:\(\sum_{i=1}^{30}(6 i-4)\).
- Відповідь
-
\(2,670\)
Знайдіть суму:\(\sum_{i=1}^{35}(5 i-3)\).
- Відповідь
-
\(3,045\)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з арифметичними послідовностями
Ключові концепції
- Загальний член (\(n\)й член) арифметичної
послідовності Загальний термін арифметичної послідовності з першим\(a_{1}\) і\(d\) спільною різницею\(a_{n}=a_{1}+(n-1) d\)
- Сума перших\(n\) членів арифметичної
послідовності Сума перших\\(n\) членів арифметичної послідовності, де\(a_{1}\) перший член і\(a_{n}\)\(n\) -й член дорівнює\(S_{n}\)\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Глосарій
- арифметична послідовність
- Арифметична послідовність - це послідовність, де різниця між послідовними долями є постійною.
- загальна відмінність
- Різниця між послідовними термінами в арифметичній послідовності\(a_{n}−a_{n−1}\)\(d\), є загальною різницею, для\(n\) більшої або рівної двом.
