9.3: Розв'яжіть квадратні рівняння, заповнивши квадрат

Цілі навчання

До кінця цього розділу ви зможете:

• Завершити квадрат біноміального виразу
• Розв'яжіть квадратні рівняння виду,\(x^{2}+bx+c=0\) заповнивши квадрат
• Розв'яжіть квадратні рівняння виду,\(ax^{2}+bx+c=0\) заповнивши квадрат

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Розгорнути:\((x+9)^{2}\).
   Якщо ви пропустили цю проблему, перегляньте приклад 5.32.
2. Фактор\(y^{2}-14 y+49\).
   Якщо ви пропустили цю проблему, перегляньте приклад 6.9.
3. Фактор\(5 n^{2}+40 n+80\).
   Якщо ви пропустили цю проблему, перегляньте приклад 6.14.

Поки що ми розв'язали квадратні рівняння шляхом факторингу та використання властивості квадратного кореня. У цьому розділі ми вирішимо квадратні рівняння процесом, який називається завершенням квадрата, що важливо для нашої роботи над коніками пізніше.

Завершити квадрат біноміального виразу

В останньому розділі ми змогли використати властивість квадратного кореня для вирішення рівняння,\((y-7)^{2}=12\) оскільки ліва сторона була ідеальним квадратом.

\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)

Ми також вирішили рівняння, в якому ліва сторона була ідеальним квадратним триноміалом, але нам довелося переписати його форму,\((x−k)^{2}\) щоб використовувати властивість Square Root.

\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)

Що станеться, якщо змінна не є частиною ідеального квадрата? Чи можемо ми використовувати алгебру, щоб зробити ідеальний квадрат?

Давайте розглянемо два приклади, які допоможуть нам розпізнати закономірності.

\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)

Ми повторюємо шаблони тут для довідки.

Визначення\(\PageIndex{1}\): Binomial Squares Pattern

Якщо\(a\) і\(b\) є дійсними числами,

Ми можемо використовувати цей візерунок, щоб «зробити» ідеальний квадрат.

Почнемо з виразу\(x^{2}+6 x\). Оскільки між двома термінами є знак плюс, ми будемо використовувати\((a+b)^{2}\) візерунок,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).

Зрештою, нам потрібно знайти останній термін цього триноміалу, який зробить його ідеальним квадратним тріноміалом. Для цього нам потрібно буде знайти\(b\). Але спочатку почнемо з визначення\(a\). Зверніть увагу, що перший член\(x^{2}+6x\) - це квадрат,\(x^{2}\). Це говорить нам про це\(a=x\).

Яке число\(b\), при множенні на\(2x\) дає\(6x\)? Це повинно було б бути\(3\), що є\(\frac{1}{2}(6)\). Отже\(b=3\).

Тепер, щоб завершити ідеальний квадратний триноміал, ми знайдемо останній термін квадратом\(b\), який є\(3^{2}=9\).

Тепер ми можемо фактор.

Таким чином, ми виявили, що додавання\(9\) до\(x^{2}+6 x\) «завершує квадрат», і ми пишемо його як\((x+3)^{2}\).

Howto: Завершити квадрат\(x^{2}+bx\)

1. Визначте\(b\), коефіцієнт\(x\).
2. Знайдіть\(\left(\frac{1}{2} b\right)^{2}\), число для завершення квадрата.
3. Додайте\(\left(\frac{1}{2} b\right)^{2}\) до\(x^{2}+bx\).
4. Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.

Приклад\(\PageIndex{1}\)

Завершіть квадрат, щоб зробити ідеальний квадратний тріноміал. Потім запишіть результат у вигляді біноміального квадрата.

1. \(x^{2}-26 x\)
2. \(y^{2}-9 y\)
3. \(n^{2}+\frac{1}{2} n\)

Рішення:

а.

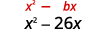Коефіцієнт\(x\) дорівнює -26.
Знайти\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\) \((13)^{2}\) 169
Додайте\(169\) до біноміалу, щоб завершити квадрат.	\(x^{2}-26 x+169\)
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.	\((x-13)^{2}\)

б.

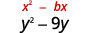Коефіцієнт\(y\) становить\(-9\).
Знайти\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\) \(\left(-\frac{9}{2}\right)^{2}\) \(\frac{81}{4}\)
Додайте\(\frac{81}{4}\) до біноміалу, щоб завершити квадрат.	\(y^{2}-9 y+\frac{81}{4}\)
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.	\(\left(y-\frac{9}{2}\right)^{2}\)

c.

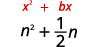Коефіцієнт\(n\) становить\(\frac{1}{2}\).
Знайти\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\) \(\left(\frac{1}{4}\right)^{2}\) \(\frac{1}{16}\)
Додайте\(\frac{1}{16}\) до біноміалу, щоб завершити квадрат.	\(n^{2}+\frac{1}{2} n+\frac{1}{16}\)
Перепишіть як біноміальний квадрат.	\(\left(n+\frac{1}{4}\right)^{2}\)

Вправа\(\PageIndex{1}\)

Завершіть квадрат, щоб зробити ідеальний квадратний тріноміал. Потім запишіть результат у вигляді біноміального квадрата.

1. \(a^{2}-20 a\)
2. \(m^{2}-5 m\)
3. \(p^{2}+\frac{1}{4} p\)

Відповідь

1. \((a-10)^{2}\)
2. \(\left(b-\frac{5}{2}\right)^{2}\)
3. \(\left(p+\frac{1}{8}\right)^{2}\)

Вправа\(\PageIndex{2}\)

Завершіть квадрат, щоб зробити ідеальний квадратний тріноміал. Потім запишіть результат у вигляді біноміального квадрата.

1. \(b^{2}-4 b\)
2. \(n^{2}+13 n\)
3. \(q^{2}-\frac{2}{3} q\)

Відповідь

1. \((b-2)^{2}\)
2. \(\left(n+\frac{13}{2}\right)^{2}\)
3. \(\left(q-\frac{1}{3}\right)^{2}\)

Розв'яжіть квадратні рівняння форми\(x^{2}+bx+c=0\) заповнивши квадрат

При вирішенні рівнянь ми завжди повинні робити одне і те ж саме з обох сторін рівняння. Це вірно, звичайно, коли ми вирішуємо квадратне рівняння, заповнюючи квадрат теж. Коли ми додаємо член до однієї сторони рівняння, щоб зробити ідеальний квадратний триноміал, ми також повинні додати той самий член до іншої сторони рівняння.

Наприклад, якщо ми почнемо з рівняння\(x^{2}+6x=40\), і ми хочемо завершити квадрат зліва, ми додамо 9 до обох сторін рівняння.

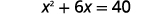Додайте\(9\) в обидві сторони, щоб завершити квадрат.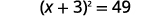

Тепер рівняння у формі для вирішення за допомогою властивості Square Root! Завершення квадрата - це спосіб перетворити рівняння у форму, яку нам потрібно мати можливість використовувати властивість Square Root.

Приклад\(\PageIndex{2}\) How to Solve a Quadratic Equation of the Form \(x^{2}+bx+x=0\) by Completing the Square

Вирішіть, заповнивши квадрат:\(x^{2}+8x=48\).

Рішення:

Крок 1: Ізолюйте змінні терміни з одного боку та постійні терміни з іншого.	Це рівняння має всі змінні зліва.	\(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\)
Крок 2: Знайдіть\(\left(\frac{1}{2} \cdot b\right)^{2}\), число, щоб завершити квадрат. Додайте його до обох сторін рівняння.	Візьміть половину\(8\) і квадрат її. \(4^{2}=16\) Додайте\(16\) до обох сторін рівняння.	\(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \) \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\)
Крок 3: Фактор ідеальний квадратний триноміал як біноміальний квадрат.	\(x^{2}+8 x+16=(x+4)^{2}\) Додайте умови праворуч.	\((x+4)^{2}=64\)
Крок 4: Використовуйте властивість квадратного кореня.		\(x+4=\pm \sqrt{64}\)
Крок 5: Спростіть радикал, а потім вирішити два результуючі рівняння.		\(x+4=\pm 8\) \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\)
Крок 6: Перевірте рішення.	Помістіть кожну відповідь у вихідне рівняння для перевірки. Замінник\(x=4\) і\(x=-12\).	\(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\) \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\)

Вправа\(\PageIndex{3}\)

Вирішіть, заповнивши квадрат:\(x^{2}+4 x=5\).

Відповідь

\(x=-5, x=-1\)

Вправа\(\PageIndex{4}\)

Вирішіть, заповнивши квадрат:\(y^{2}−10y=−9\).

Відповідь

\(y=1, y=9\)

Кроки для вирішення квадратного рівняння шляхом заповнення квадрата наведені тут.

Розв'яжіть квадратне рівняння форми\(x^{2}+bx+c=0\) заповнивши квадрат

1. Виділяють змінні члени з одного боку, а постійні - з іншого.
2. Знайдіть\(\left(\frac{1}{2} \cdot b\right)^{2}\), число, необхідне для завершення квадрата. Додайте його до обох сторін рівняння.
3. Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат ліворуч і спростити, додавши терміни праворуч
4. Використовуйте властивість «Квадратний корінь».
5. Спростити радикал, а потім вирішити два результуючих рівняння.
6. Перевірте рішення.

Коли ми вирішуємо рівняння шляхом заповнення квадрата, відповіді не завжди будуть цілими числами.

Приклад\(\PageIndex{3}\)

Вирішіть, заповнивши квадрат:\(x^{2}+4 x=-21\).

Рішення:

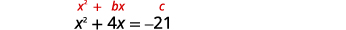Терміни змінної знаходяться з лівого боку. Візьміть половину\(4\) і квадрат її.
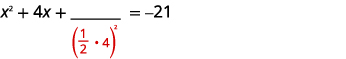\(\left(\frac{1}{2}(4)\right)^{2}=4\)
Додайте\(4\) в обидві сторони.
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.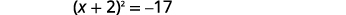
Використовуйте властивість «Квадратний корінь».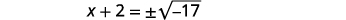
Спрощення за допомогою комплексних чисел.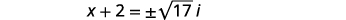
Відніміть\(2\) з кожного боку.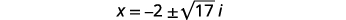
Перепишіть, щоб показати два рішення.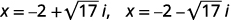
Ми залишаємо чек вам.

Вправа\(\PageIndex{5}\)

Вирішіть, заповнивши квадрат:\(y^{2}-10 y=-35\).

Відповідь

\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)

Вправа\(\PageIndex{6}\)

Вирішіть, заповнивши квадрат:\(z^{2}+8 z=-19\).

Відповідь

\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)

У попередньому прикладі наші розв'язки були комплексними числами. У наступному прикладі розв'язками будуть ірраціональні числа.

Приклад\(\PageIndex{4}\)

Вирішіть, заповнивши квадрат:\(y^{2}-18 y=-6\).

Рішення:

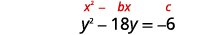Терміни змінної знаходяться з лівого боку. Візьміть половину\(-18\) і квадрат її.
\(\left(\frac{1}{2}(-18)\right)^{2}=81\)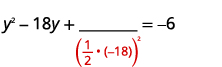
Додайте\(81\) в обидві сторони.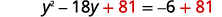
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.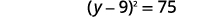
Використовуйте властивість «Квадратний корінь».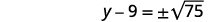
Спростити радикал.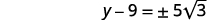
Вирішити для\(y\).
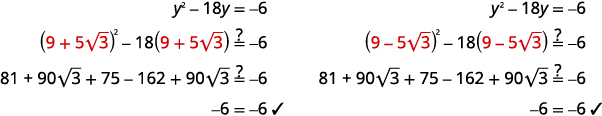
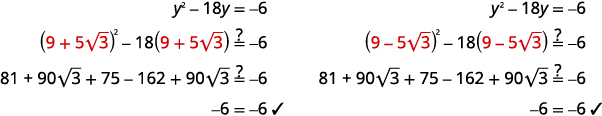Перевірте. Малюнок 9.2.35

Ще одним способом перевірити це було б використання калькулятора. Оцініть\(y^{2}−18y\) для обох рішень. Відповідь повинна бути\(−6\).

Вправа\(\PageIndex{7}\)

Вирішіть, заповнивши квадрат:\(x^{2}-16 x=-16\).

Відповідь

\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)

Вправа\(\PageIndex{8}\)

Вирішіть, заповнивши квадрат:\(y^{2}+8 y=11\).

Відповідь

\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)

Наступний приклад ми почнемо з виділення змінних членів в лівій частині рівняння.

Приклад\(\PageIndex{5}\)

Вирішіть, заповнивши квадрат:\(x^{2}+10 x+4=15\).

Рішення:

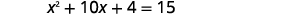Виділіть змінні терміни з лівого боку. Відніміть,\(4\) щоб отримати постійні терміни з правого боку.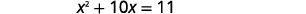
Візьміть половину\(10\) і квадрат її.
\(\left(\frac{1}{2}(10)\right)^{2}=25\)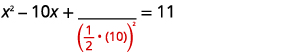
Додайте\(25\) в обидві сторони.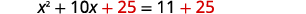
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.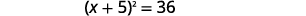
Використовуйте властивість «Квадратний корінь».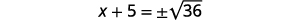
Спростити радикал.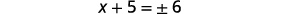
Вирішити для\(x\).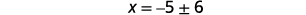
Перепишіть, щоб показати два рішення.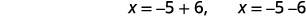
Розв'яжіть рівняння.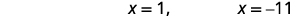
Перевірка: 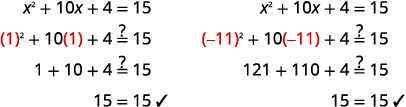Малюнок 9.2.47

Вправа\(\PageIndex{9}\)

Вирішіть, заповнивши квадрат:\(a^{2}+4 a+9=30\).

Відповідь

\(a=-7, a=3\)

Вправа\(\PageIndex{10}\)

Вирішіть, заповнивши квадрат:\(b^{2}+8 b-4=16\).

Відповідь

\(b=-10, b=2\)

Щоб вирішити наступне рівняння, ми повинні спочатку зібрати всі змінні члени в лівій частині рівняння. Далі діємо так, як ми це робили в попередніх прикладах.

Приклад\(\PageIndex{6}\)

Вирішіть, заповнивши квадрат:\(n^{2}=3 n+11\).

Рішення:

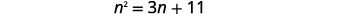Відніміть\(3n\), щоб отримати змінні терміни з лівого боку.
Візьміть половину\(-3\) і квадрат її.
\(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\)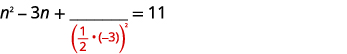
Додайте\(\frac{9}{4}\) в обидві сторони.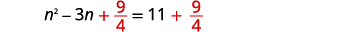
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.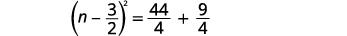
Додайте дроби з правого боку.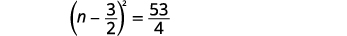
Використовуйте властивість «Квадратний корінь».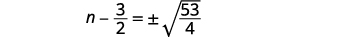
Спростити радикал.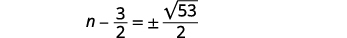
Вирішити для\(n\).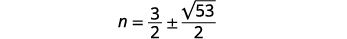
Перепишіть, щоб показати два рішення.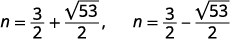
Перевірка: Ми залишаємо чек для вас!

Вправа\(\PageIndex{11}\)

Вирішіть, заповнивши квадрат:\(p^{2}=5 p+9\).

Відповідь

\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)

Вправа\(\PageIndex{12}\)

Вирішіть, заповнивши квадрат:\(q^{2}=7 q-3\).

Відповідь

\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)

Зверніть увагу, що ліва частина наступного рівняння знаходиться в факторальному вигляді. Але права сторона - це не нуль. Отже, ми не можемо використовувати властивість нульового продукту, оскільки вона говорить «Якщо\(a⋅b=0\), то\(a=0\) чи»\(b=0\). Замість цього ми множимо коефіцієнти, а потім ставимо рівняння в стандартну форму для вирішення, заповнивши квадрат.

Приклад\(\PageIndex{7}\)

Вирішіть, заповнивши квадрат:\((x-3)(x+5)=9\).

Рішення:

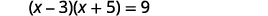Множимо біноми зліва.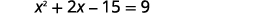
Додайте\(15\), щоб виділити константні терміни праворуч.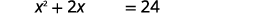
Візьміть половину\(2\) і квадрат її.
\(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\)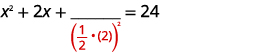
Додайте\(1\) в обидві сторони.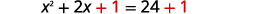
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.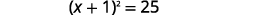
Використовуйте властивість «Квадратний корінь».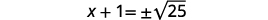
Вирішити для\(x\).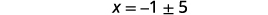
Перепишіть, щоб показати два рішення.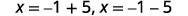
Спростити.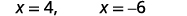
Перевірка: Ми залишаємо чек для вас!

Вправа\(\PageIndex{13}\)

Вирішіть, заповнивши квадрат:\((c-2)(c+8)=11\).

Відповідь

\(c=-9, c=3\)

Вправа\(\PageIndex{14}\)

Вирішіть, заповнивши квадрат:\((d-7)(d+3)=56\).

Відповідь

\(d=11, d=-7\)

Розв'яжіть квадратні рівняння форми\(ax^{2}+bx+c=0\) заповнивши квадрат

Процес заповнення квадрата найкраще працює, коли коефіцієнт\(x^{2}\) є\(1\), тому ліва частина рівняння має вигляд\(x^{2}+bx+c\). Якщо\(x^{2}\) термін має коефіцієнт, відмінний\(1\), робимо кілька попередніх кроків, щоб коефіцієнт був рівним\(1\).

Іноді коефіцієнт може бути врахований з усіх трьох членів триноміала. Це буде наша стратегія в наступному прикладі.

Приклад\(\PageIndex{8}\)

Вирішіть, заповнивши квадрат:\(3 x^{2}-12 x-15=0\).

Рішення:

Щоб завершити квадрат, нам потрібен коефіцієнт\(x^{2}\) повинен бути один. Якщо ми перерахуємо коефіцієнт\(x^{2}\) як загальний коефіцієнт, ми можемо продовжити рішення рівняння, заповнивши квадрат.

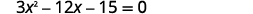Фактор з найбільшого загального фактора.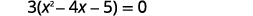
Розділіть обидві сторони на,\(3\) щоб виділити триноміал з коефіцієнтом\(1\).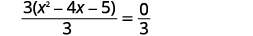
Спростити.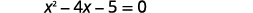
Додайте,\(5\) щоб отримати постійні терміни з правого боку.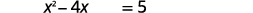
Візьміть половину\(4\) і квадрат її.
\(\left(\frac{1}{2}(-4)\right)^{2}=4\)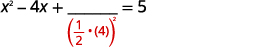
Додайте\(4\) в обидві сторони.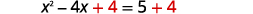
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.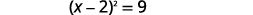
Використовуйте властивість «Квадратний корінь».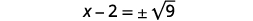
Вирішити для\(x\).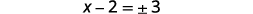
Перепишіть, щоб показати два рішення.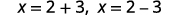
Спростити.
Перевірка: 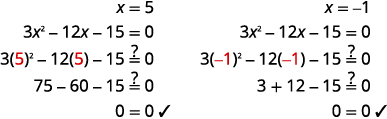Малюнок 9.2.80

Вправа\(\PageIndex{15}\)

Вирішіть, заповнивши квадрат:\(2 m^{2}+16 m+14=0\).

Відповідь

\(m=-7, m=-1\)

Вправа\(\PageIndex{16}\)

Вирішіть, заповнивши квадрат:\(4 n^{2}-24 n-56=8\).

Відповідь

\(n=-2, n=8\)

Щоб завершити квадрат, коефіцієнт\(x^{2}\) повинен бути\(1\). Коли провідний коефіцієнт не є коефіцієнтом всіх членів, ми розділимо обидві сторони рівняння на провідний коефіцієнт! Це дасть нам частку для другого коефіцієнта. Ми вже бачили, як завершити квадрат дробами в цьому розділі.

Приклад\(\PageIndex{9}\)

Вирішіть, заповнивши квадрат:\(2 x^{2}-3 x=20\).

Рішення:

Для завершення квадрата нам потрібен коефіцієнт\(x^{2}\) повинен бути один. Ми розділимо обидві сторони рівняння на коефіцієнт\(x^{2}\). Потім ми можемо продовжити рішення рівняння, заповнивши квадрат.

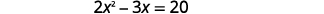Розділіть обидві сторони на,\(2\) щоб отримати\(x^{2}\) коефіцієнт бути\(1\).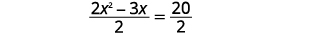
Спростити.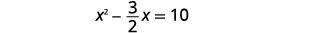
Візьміть половину\(-\frac{3}{2}\) і квадрат її.
\(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\)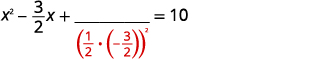
Додайте\(\frac{9}{16}\) в обидві сторони.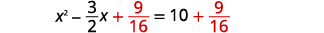
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.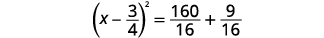
Додайте дроби з правого боку.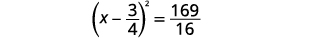
Використовуйте властивість «Квадратний корінь».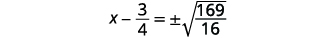
Спростити радикал.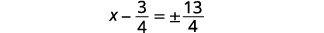
Вирішити для\(x\).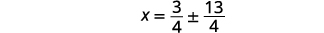
Перепишіть, щоб показати два рішення.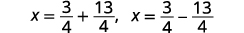
Спростити.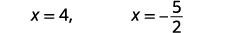
Перевірка: Ми залишаємо чек для вас!

Вправа\(\PageIndex{17}\)

Вирішіть, заповнивши квадрат:\(3 r^{2}-2 r=21\).

Відповідь

\(r=-\frac{7}{3}, r=3\)

Вправа\(\PageIndex{18}\)

Вирішіть, заповнивши квадрат:\(4 t^{2}+2 t=20\).

Відповідь

\(t=-\frac{5}{2}, t=2\)

Тепер, коли ми побачили, що коефіцієнт\(x^{2}\) повинен бути\(1\) для нас, щоб завершити квадрат, ми оновлюємо нашу процедуру вирішення квадратного рівняння, заповнивши квадрат, щоб включити рівняння форми\(a x^{2}+b x+c=0\).

Howto: Розв'язувати квадратне рівняння форми\(a x^{2}+b x+c=0\) by Completing the Square

1. Ділимо на аа, щоб зробити коефіцієнт\(x^{2}\) терміну\(1\).
2. Виділяють змінні члени з одного боку, а постійні - з іншого.
3. Знайдіть\(\left(\frac{1}{2} \cdot b\right)^{2}\), число, необхідне для завершення квадрата. Додайте його до обох сторін рівняння.
4. Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат ліворуч і спростити, додавши терміни праворуч
5. Використовуйте властивість «Квадратний корінь».
6. Спростити радикал, а потім вирішити два результуючих рівняння.
7. Перевірте рішення.

Приклад\(\PageIndex{10}\)

Вирішіть, заповнивши квадрат:\(3 x^{2}+2 x=4\).

Рішення:

Знову ж таки, першим нашим кроком буде зробити коефіцієнт\(x^{2}\) одиниці. Розділивши обидві сторони рівняння на коефіцієнт\(x^{2}\), ми можемо потім продовжити рішення рівняння, заповнивши квадрат.

Розділіть обидві сторони на\(3\), щоб коефіцієнт був\(x^{2}\) рівним\(1\).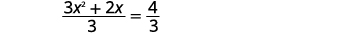
Спростити.
Візьміть половину\(\frac{2}{3}\) і квадрат її.
\(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\)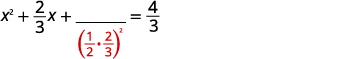
Додайте\(\frac{1}{9}\) в обидві сторони.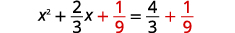
Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат.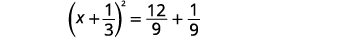
Використовуйте властивість «Квадратний корінь».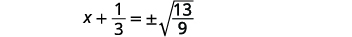
Спростити радикал.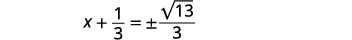
Вирішити для\(x\).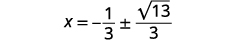
Перепишіть, щоб показати два рішення.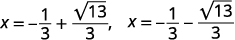
Перевірка: Ми залишаємо чек для вас!

Вправа\(\PageIndex{19}\)

Вирішіть, заповнивши квадрат:\(4 x^{2}+3 x=2\).

Відповідь

\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)

Вправа\(\PageIndex{20}\)

Вирішіть, заповнивши квадрат:\(3 y^{2}-10 y=-5\).

Відповідь

\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)

Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з заповненням площі.

• Завершення ідеальних квадратних триноміалів
• Завершення площі 1
• Завершення квадрата для розв'язання квадратних рівнянь
• Завершення квадрата для розв'язання квадратних рівнянь: більше прикладів
• Завершення площі 4

Ключові концепції

• Біноміальні квадрати шаблон
  Якщо\(a\) і\(b\) є дійсними числами,

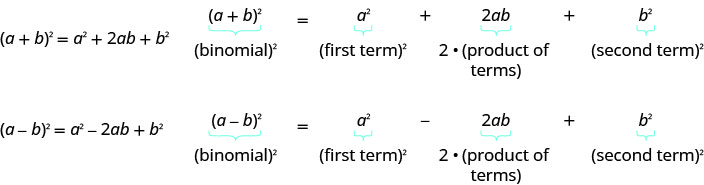
• Як завершити квадрат
  1. Визначте\(b\), коефіцієнт\(x\).
  2. Знайдіть\(\left(\frac{1}{2} b\right)^{2}\), число для завершення квадрата.
  3. Додайте\(\left(\frac{1}{2} b\right)^{2}\) до\(x^{2}+bx\)
  4. Перепишіть триноміал як біноміальний квадрат
• Як вирішити квадратне рівняння виду, \(a x^{2}+b x+c=0\)заповнивши квадрат.
  1. Розділити на\(a\), щоб зробити коефіцієнт\(x^{2}\) терміну\(1\).
  2. Виділяють змінні члени з одного боку, а постійні - з іншого.
  3. Знайдіть\(\left(\frac{1}{2} \cdot b\right)^{2}\), число, необхідне для завершення квадрата. Додайте його до обох сторін рівняння.
  4. Фактор ідеальний квадратний триноміал, записуючи його як біноміальний квадрат ліворуч і спростити, додавши терміни праворуч.
  5. Використовуйте властивість «Квадратний корінь».
  6. Спростити радикал, а потім вирішити два результуючих рівняння.
  7. Перевірте рішення.