7.7: Вирішити раціональні нерівності
- Page ID
- 59791
- Вирішити раціональні нерівності
- Розв'яжіть нерівність за допомогою раціональних функцій
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Знайдіть значення wh\(x-5\) ⓐ\(x=6\) ⓑ\(x=-3\) ⓒ\(x=5\)
Якщо ви пропустили цю проблему, перегляньте приклад 1.2.16. - Вирішення:\(8-2 x<12\)
Якщо ви пропустили цю проблему, перегляньте приклад 2.6.13. - Напишіть інтервальне позначення:\(-3 \leq x<5 \)
Якщо ви пропустили цю проблему, перегляньте приклад 2.6.4.
Вирішити раціональні нерівності
Ми навчилися розв'язувати лінійні нерівності, навчившись розв'язувати лінійні рівняння. Методи були дуже однаковими за одним великим винятком. Коли ми множимо або ділимо на негативне число, знак нерівності змінився.
Щойно навчившись розв'язувати раціональні рівняння, ми готові вирішувати раціональні нерівності. Раціональна нерівність - це нерівність, яка містить раціональний вираз.
Раціональна нерівність - це нерівність, яка містить раціональний вираз.
Нерівності, такі як\(\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad\) і\(\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad \) є раціональними нерівностями, оскільки кожна з них містить раціональний вираз.
Коли ми вирішимо раціональну нерівність, ми будемо використовувати багато методів вирішення лінійних нерівностей. Особливо потрібно пам'ятати, що коли ми множимо або ділимо на негативне число, знак нерівності повинен змінитися.
Інша відмінність полягає в тому, що ми повинні ретельно розглянути, яке значення може зробити раціональний вираз невизначеною і тому має бути виключено.
Коли ми вирішуємо рівняння і результат є\(x=3\), ми знаємо, що є одне рішення, яке 3.
Коли ми вирішуємо нерівність і результат є\(x>3\), ми знаємо, що існує багато рішень. Ми графуємо результат, щоб краще показати всі рішення, і ми починаємо з 3. Три стає критичною точкою і тоді ми вирішуємо, чи варто затінювати ліворуч або праворуч від неї. Числа праворуч від 3 більше, ніж 3, тому ми затінюємо праворуч.

Щоб вирішити раціональну нерівність, ми спочатку повинні записати нерівність лише з одним часткою ліворуч і 0 праворуч.
Далі визначаємо критичні точки, які потрібно використовувати для поділу числової лінії на інтервали. Критичною точкою є число, яке робить раціональний вираз нульовим або невизначеним.
Потім ми оцінимо множники чисельника і знаменника, і знайдемо частку в кожному інтервалі. Це дозволить визначити інтервал, або інтервали, який містить всі розв'язки раціональної нерівності.
Ми пишемо рішення в інтервальному позначенні з обережністю, щоб визначити, чи включені кінцеві точки.
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{x-1}{x+3} \geq 0\)
Рішення
Крок 1. Запишіть нерівність як один коефіцієнт зліва і нуль праворуч.
Наша нерівність знаходиться в такому вигляді. \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Крок 2. Визначте критичні точки — точки, де раціональний вираз буде нульовим або невизначеним.
Раціональний вираз буде дорівнює нулю, коли чисельник дорівнює нулю. З\(x-1=0\) коли\(x=1\), то 1 - це критична точка.
Раціональний вираз буде невизначено, коли знаменник дорівнює нулю. З\(x+3=0\) коли\(x=-3\), то -3 є критичною точкою.
Критичні точки - 1 і -3.
Крок 3. Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
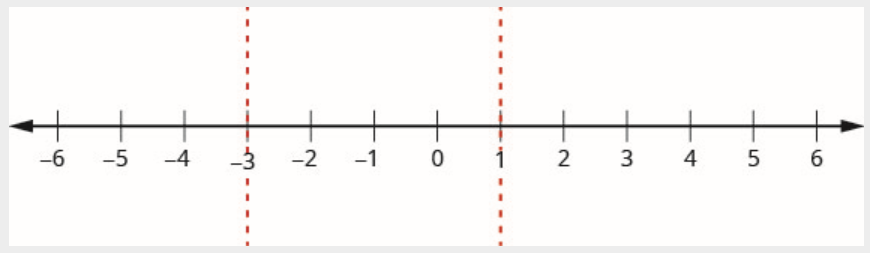
Числовий рядок ділиться на три інтервали:
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]
Крок 4. Перевірте значення в кожному інтервалі. Над числовим рядком показують знак кожного множника раціонального виразу в кожному інтервалі. Під числовим рядком показуємо знак частки.
Щоб знайти знак кожного фактора в інтервалі, ми вибираємо будь-яку точку в цьому інтервалі і використовуємо її як контрольну точку. Будь-яка точка в інтервалі дасть вираз той же знак, тому ми можемо вибрати будь-яку точку в інтервалі.
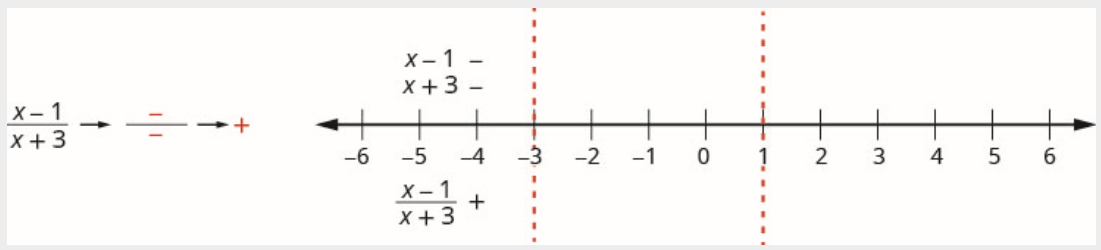
\[\text { Interval }(-\infty,-3) \nonumber \]
Число -4 знаходиться в інтервалі\((-\infty,-3)\). Перевірте\(x=-4\) в виразі в чисельнику і знаменнику.
Чисельник:
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]
Знаменник:
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Над цифровим рядком відзначте коефіцієнт\(x-1\) негативний і позначте коефіцієнт\(x+3\) негативний.
Оскільки негатив, розділений на негатив, є позитивним, позначте частку позитивним в інтервалі\((-\infty,-3)\)
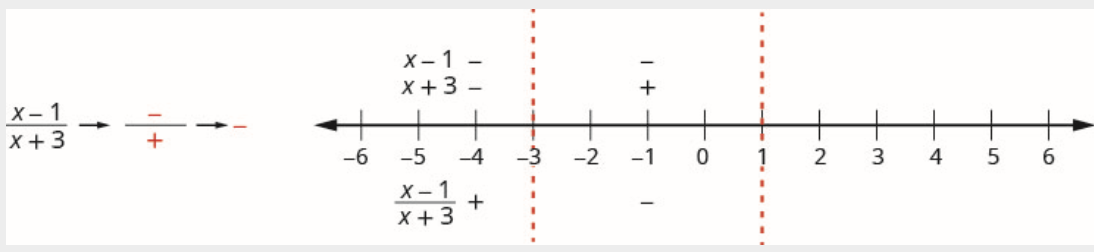
\[\text {Interval } (-3,1) \nonumber \]
Число 0 знаходиться в інтервалі\((-3,1)\). Тест\(x=0\).
Чисельник:
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Знаменник:
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]
Над цифровим рядком відзначте коефіцієнт\(x-1\) негативний і позначте\(x+3\) позитивний.
Оскільки негатив, розділений на позитив, є негативним, частка позначається негативним в інтервалі\((-3,1)\).
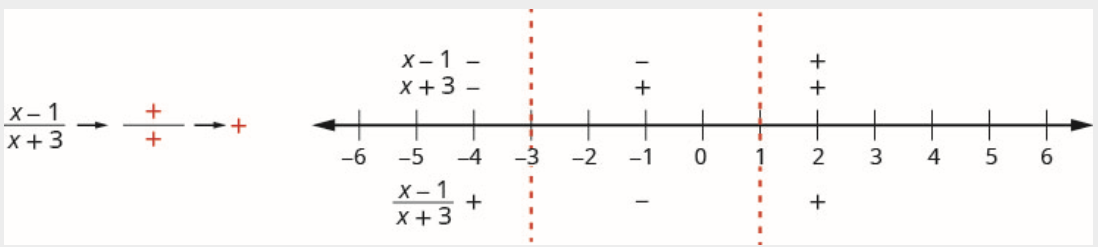
\[\text {Interval }(1, \infty) \nonumber \]
Число 2 знаходиться в проміжку\((1, \infty)\). Тест\(x=2\).
Чисельник:
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
Знаменник:
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]
Над цифровим рядком відзначте коефіцієнт\(x-1\) позитивний і позначте\(x+3\) позитивний.
Оскільки позитивне, поділене на позитивне, є позитивним, позначте коефіцієнт позитивний в інтервалі\((1, \infty)\).
Крок 5. Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.
Ми хочемо, щоб частка була більше або дорівнює нулю, тому числа в інтервалах\((-\infty,-3)\) і\((1, \infty) \) є розв'язками.
Але як щодо критичних моментів?
Критична точка\(x=-3\) робить знаменник 0, тому її потрібно виключити з рішення і відзначати його дужками.
Критична точка\(x=1\) робить весь раціональний вираз 0. Нерівність вимагає, щоб раціональний вираз був більшим або рівним. Отже, 1 частина розчину і розмічаємо його скобою.
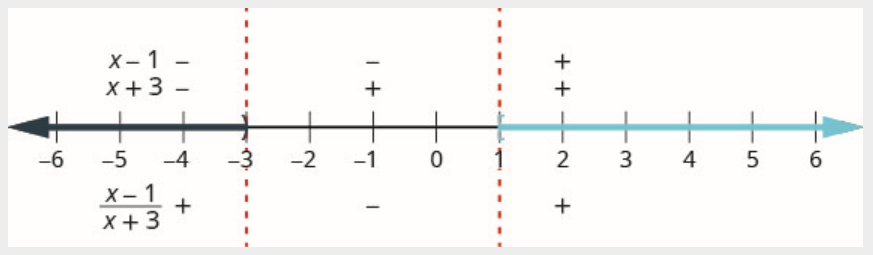
Нагадаємо, що коли у нас є рішення, що складається з більш ніж одного інтервалу, ми використовуємо символ об'єднання\(\cup \), щоб з'єднати два інтервали. Рішення в інтервальних позначеннях є\((-\infty,-3) \cup[1, \infty)\).
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{x-2}{x+4} \geq 0\)
- Відповідь
-
\((-\infty,-4) \cup[2, \infty)\)
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{x+2}{x-4} \geq 0\)
- Відповідь
-
\((-\infty,-2] \cup(4, \infty)\)
Ми підсумовуємо кроки для зручності ознайомлення.
Крок 1. Запишіть нерівність як один коефіцієнт зліва і нуль праворуч.
Крок 2. Визначте критичні точки — точки, де раціональний вираз буде нульовим або невизначеним.
Крок 3. Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
Крок 4. Перевірте значення в кожному інтервалі. Над числовим рядком показують знак кожного множника чисельника і знаменника в кожному інтервалі. Під числовим рядком показуємо знак частки.
Крок 5. Визначте інтервали, де нерівність правильна. Запишіть рішення в інтервальних позначеннях.
Наступний приклад вимагає, щоб ми спочатку отримали раціональну нерівність в правильну форму.
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{4 x}{x-6}<1\)
Рішення
\[\dfrac{4 x}{x-6}<1 \nonumber \]
Відніміть 1, щоб отримати нуль праворуч.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Перепишіть 1 як дріб за допомогою РК-дисплея.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Відніміть чисельники і помістіть різницю над спільним знаменником.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Спростити.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Фактор чисельника, щоб показати всі фактори.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Знайдіть критичні точки.
Коефіцієнт буде дорівнює нулю, коли чисельник дорівнює нулю. Коефіцієнт невизначений, коли знаменник дорівнює нулю.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]
Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
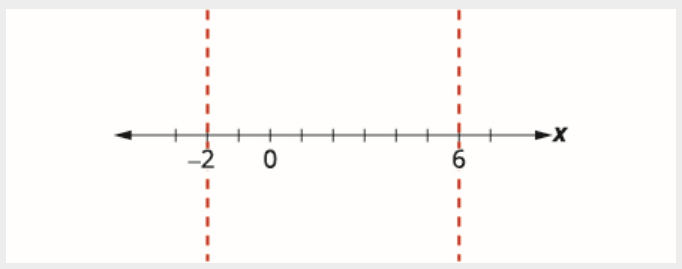
Перевірте значення в кожному інтервалі.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(x+2)\) | \ (-\ infty, -2)\)» style="вертикальне вирівнювання: середній;» клас = "lt-math-5164">
х+2 -3+2 -1 - |
\ ((-2,6)\)» style="вертикальне вирівнювання: середина;» клас = "lt-math-5164">
х+2 0+2 2 + |
\ (6,\ infty)\)» style="вертикальне вирівнювання: середина;» клас = "lt-math-5164">
х+2 7+2 9 + |
| \(x-6\) | \ (-\ infty, -2)\)» style="вертикальне вирівнювання: середній;» клас = "lt-math-5164">
х-6 -3-6 -9 - |
\ ((-2,6)\)» style="вертикальне вирівнювання: середина;» клас = "lt-math-5164">
х-6 0-6 -6 - |
\ (6,\ infty)\)» style="вертикальне вирівнювання: середина;» клас = "lt-math-5164">
х-6 7-6 1 + |
Над числовим рядком показують знак кожного множника раціонального виразу в кожному інтервалі. Під числовим рядком показуємо знак частки.
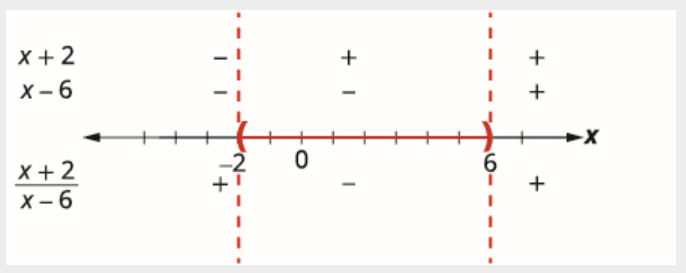
Визначте інтервали, де нерівність правильна. Ми хочемо, щоб частка була від'ємною, тому розв'язок включає точки між −2 та 6. Оскільки нерівність строго менше, кінцеві точки не включаються.
Запишемо розв'язок в інтервальному позначенні як (−2, 6).
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{3 x}{x-3}<1\).
- Відповідь
-
\(\left(-\dfrac{3}{2}, 3\right)\)
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{3 x}{x-4}<2\).
- Відповідь
-
\((-8,4)\)
У наступному прикладі чисельник завжди позитивний, тому знак раціонального виразу залежить від знака знаменника.
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{5}{x^{2}-2 x-15}>0\).
Рішення
Нерівність знаходиться в правильній формі.
\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]
Фактор знаменника.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Знайдіть критичні точки. Коефіцієнт дорівнює 0, коли чисельник дорівнює 0. Оскільки чисельник завжди дорівнює 5, частка не може бути 0.
Коефіцієнт буде невизначений, коли знаменник дорівнює нулю.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
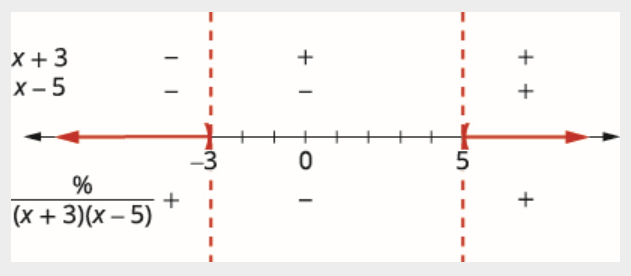
Тестові значення в кожному інтервалі. Над числовим рядком покажіть знак кожного множника знаменника в кожному інтервалі. Нижче числового рядка покажіть знак частки.
Запишіть рішення в інтервальних позначеннях.
\[(-\infty,-3) \cup(5, \infty) \nonumber \]
Solve and write the solution in interval notation: \(\dfrac{1}{x^{2}+2 x-8}>0\).
- Answer
-
\((-\infty,-4) \cup(2, \infty)\)
Solve and write the solution in interval notation: \(\dfrac{3}{x^{2}+x-12}>0 \).
- Answer
-
\((-\infty,-4) \cup(3, \infty)\)
The next example requires some work to get it into the needed form.
Solve and write the solution in interval notation: \(\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}\).
Solution
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]
Subtract \(\dfrac{5}{3 x}\) to get zero on the right.
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]
Rewrite to get each fraction with the LCD
\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]
Simplify.
\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]
Subtract the numerators and place the difference over the common denominator.
\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]
Factor the numerator.
\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]
Find the critical points.
\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]
Use the critical points to divide the number line into intervals.
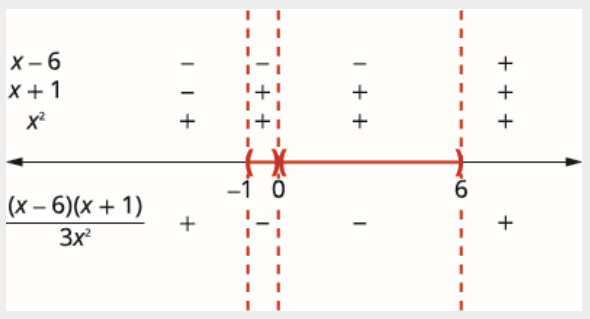
Над числовим рядком покажіть знак кожного фактора в кожному інтервалі. Нижче числового рядка покажіть знак частки.
Оскільки, 0 виключається, то рішенням є два\((-1,0) \cup(0,6)\) інтервали,\((-1,0)\) і\((0,6)\).
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}\).
- Відповідь
-
\((2,4)\)
Розв'яжіть і запишіть рішення в інтервальних позначеннях:\(\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}\).
- Відповідь
-
\((3,6)\)
Розв'язуйте нерівність за допомогою раціональних функцій
При роботі з раціональними функціями іноді корисно знати, коли функція більше або менше конкретного значення. Це призводить до раціональної нерівності.
За даними функції\(R(x)=\dfrac{x+3}{x-5}\) знайдіть значення x, які роблять функцію меншою або рівною 0.
Рішення
Ми хочемо, щоб функція була менше або дорівнює 0.
\[R(x) \leq 0 \nonumber \]
Підставте раціональний вираз для\(R(x)\).
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Знайдіть критичні точки.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Використовуйте критичні точки, щоб розділити числову лінію на інтервали.
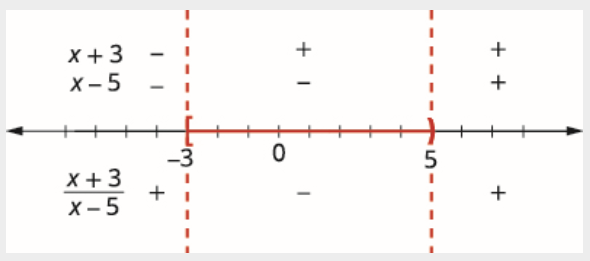
Тестові значення в кожному інтервалі. Над числовим рядком покажіть знак кожного фактора в кожному інтервалі. Нижче числового рядка покажіть знак частки. Запишіть рішення в інтервальних позначеннях. Так як 5 виключається ми, не включаємо його в інтервал.
\[[-3,5) \nonumber \]
Given the function \(R(x)=\dfrac{x-2}{x+4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\((-4,2]\)
Given the function \(R(x)=\dfrac{x+1}{x-4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\([-1,4)\)
In economics, the function \(C(x)\) is used to represent the cost of producing \(x\) units of a commodity. The average cost per unit can be found by dividing \(C(x)\) by the number of items \(x\). Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).
The function\(C(x)=10 x+3000\) represents the cost to produce \(x\), number of items. Find:
- The average cost function, \(c(x)\)
- How many items should be produced so that the average cost is less than $40.
Solution
- \[C(x)=10 x+3000 \nonumber \]
The average cost function is \(c(x)=\dfrac{C(x)}{x})\). To find the average cost function, divide the cost function by \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
The average cost function is \(c(x)=\dfrac{10 x+3000}{x} \)
- We want the function \(c(x)\) to be less than 40.
\[c(x)<40 \nonumber \]
Substitute the rational expression forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Subtract 40 to get 0 on the right.
\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]
Rewrite the left side as one quotient by finding the LCD and performing the subtraction.
\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]
Factor the numerator to show all factors.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]
Find the critical points.
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
More than 100 items must be produced to keep the average cost below $40 per item.
The function\(C(x)=20 x+6000\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $60.
- Answer
-
- \(c(x)=\dfrac{20 x+6000}{x}\)
- More than 150 items must be produced to keep the average cost below $60 per item.
The function\(C(x)=5 x+900\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $20.
- Answer
-
- \(c(x)=\dfrac{5 x+900}{x}\)
- More than 60 items must be produced to keep the average cost below $20 per item.
