5.4: Бібліотека функцій
- Page ID
- 58363
Знання графіків загальних функцій допомагає студенту візуалізувати функцію та з'єднати зв'язок між рівнянням та його графіком.
Бібліотека функцій являє собою набір функцій, який розрізняє зв'язок між функціями та їх графіками, що включає область для кожної функції.
Бібліотека функцій зростає в міру того, як ми ознайомимося з різними типами функцій. Коли ми беремо математику більш високого рівня, бібліотека стає дуже великою, але для цього розділу ми починаємо з бібліотеки, яка містить шість важливих основних функцій: лінія, парабола, кубічна, абсолютна величина, раціональна, квадратний корінь.
Графіки функцій в бібліотеці функцій - це загальні графіки функцій, а не окремі графіки функцій. Отже, ми можемо використовувати точкову графіку, технологію або перетворення для графіка певних функцій, але ми схильні запам'ятовувати загальну форму, оскільки в математиці вищого рівня корисно швидко згадати бібліотеку функцій.
Графік\(f(x) = x\)\(g(x) = 2\),\(h(x) = −3x + 1\) і визначити їх домен.
Рішення
Зверніть увагу, всі три функції є лінійними функціями. Ми можемо легко розкласти їх на одній сітці. Ми бачимо, що всі графіки є лініями, і оскільки немає обмежень до жодної з рядків, домен - це всі дійсні числа або\((−∞, ∞)\). Оскільки\(f\) це лінія через початок (\(y\)-intercept дорівнює нулю), і кожна\(x\) координата така ж, як і її відповідна\(y\) координата, наприклад,\((0, 0),\: (1, 1),\) і т.д., то ми\(f\) викликаємо функцію ідентичності.

Оскільки\(g\) це горизонтальна лінія,\(y\) координати ніколи не змінюються, і немає зміни нахилу, тобто нахил дорівнює нулю, то ми викликаємо\(g\) постійну функцію.
Функція\(h\) являє собою рівняння прямої з ненульовим нахилом і ненульовим\(y\) -перехопленням, і ми називаємо\(h\) лінійну функцію.
Графік\(f(x) = |x|\) і визначення домену.
Рішення
Давайте виберемо п'ять\(x\) -координат, і знайдемо відповідні\(y\) -значення. Кожен\(x\) -value є позитивним або негативним, і нуль. Це звичайна практика, але не обов'язкова.
| \(x\) | \(f(x)=|x|\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-2\) | \ (f (x) =|х |\) ">\(f(\color{blue}{-2}\color{black}{})=2\) | \ (x, f (x))\) ">\((-2,2)\) |
| \ (x\) ">\(-1\) | \ (f (x) =|х |\) ">\(f(\color{blue}{-1}\color{black}{})=1\) | \ (x, f (x))\) ">\((-1,1)\) |
| \ (x\) ">\(0\) | \ (f (x) =|х |\) ">\(f(\color{blue}{0}\color{black}{})=0\) | \ (x, f (x))\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =|х |\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x))\) ">\((1,1)\) |
| \ (x\) ">\(2\) | \ (f (x) =|х |\) ">\(f(\color{blue}{2}\color{black}{})=2\) | \ (x, f (x))\) ">\((2,2)\) |
Побудуйте п'ять впорядкованих пар з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Цей графік виглядає як дві лінії протилежних нахилів, які зустрічаються біля початку. Отже, це графік два рядки, які зустрічаються на початку, але зупинка там, де він зустрічається, щоб зробити v-подібний називається функція абсолютного значення Оскільки ми бачимо, що немає ніяких обмежень до графіка, домен є всі дійсні числа або\((−∞, ∞)\).
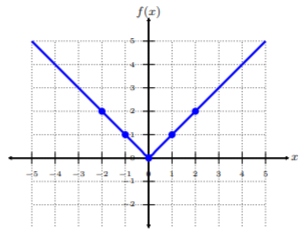
Графік\(f(x) = x^2\) і визначення домену.
Рішення
Давайте виберемо п'ять\(x\) -координат, і знайдемо відповідні\(y\) -значення. Кожне\(x\) -значення є позитивним, негативним і нульовим. Це звичайна практика, але не обов'язкова.
| \(x\) | \(f(x)=x^2\) | \((x,f(x)\) |
|---|---|---|
| \ (x\) ">\(-2\) | \ (f (x) =х^2\) ">\(f(\color{blue}{-2}\color{black}{})=4\) | \ (x, f (x)\) ">\((-2,4)\) |
| \ (x\) ">\(-1\) | \ (f (x) =х^2\) ">\(f(\color{blue}{-1}\color{black}{})=1\) | \ (x, f (x)\) ">\((-1,1)\) |
| \ (x\) ">\(0\) | \ (f (x) =х^2\) ">\(f(\color{blue}{0}\color{black}{})=0\) | \ (x, f (x)\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =х^2\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x)\) ">\((1,1)\) |
| \ (x\) ">\(2\) | \ (f (x) =х^2\) ">\(f(\color{blue}{2}\color{black}{})=4\) | \ (x, f (x)\) ">\((2,4)\) |
Побудуйте п'ять впорядкованих пар з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Цей графік називається параболою і оскільки ця функція досить поширена для\(x^2\) -форми, ми називаємо її квадратичною (квадратною) функцією. Оскільки ми бачимо, що немає обмежень на графік, домен - це всі дійсні числа або\((−∞, ∞)\).
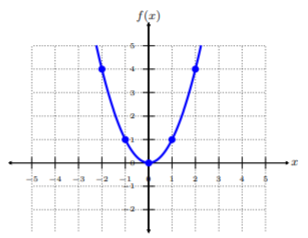
Графік\(f(x) = x^3\) і визначення домену.
Рішення
Давайте виберемо три\(x\) -координати, і знайдемо відповідні\(y\) -значення. Кожне\(x\) -значення є позитивним, негативним і нульовим. Це звичайна практика, але не обов'язкова.
| \(x\) | \(f(x)=x^3\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-1\) | \ (f (x) =х^3\) ">\(f(\color{blue}{-1}\color{black}{})=-1\) | \ (x, f (x))\) ">\((-1,-1)\) |
| \ (x\) ">\(0\) | \ (f (x) =х^3\) ">\(f(\color{blue}{0}\color{black}{})=0\) | \ (x, f (x))\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =х^3\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x))\) ">\((1,1)\) |
Побудуйте замовлені-пари з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Оскільки ця функція досить поширена для\(x^3\) -form, ми називаємо її функцією cube (cubic). Оскільки ми бачимо, що немає обмежень на графік, домен - це всі дійсні числа або\((−∞, ∞)\).

Графік\(f(x) =\sqrt{x}\) і визначення домену.
Рішення
Давайте виберемо три\(x\) -координати, і знайдемо відповідні\(y\) -значення.
| \(x\) | \(f(x)=\sqrt{x}\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(0\) | \ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{0}\color{black}{})=0\) | \ (x, f (x))\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x))\) ">\((1,1)\) |
| \ (x\) ">\(4\) | \ (f (x) =\ sqrt {x}\) ">\(f(\color{blue}{4}\color{black}{})=2\) | \ (x, f (x))\) ">\((4,2)\) |
Побудуйте замовлені-пари з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Оскільки ця функція досить поширена для\(\sqrt{x}\) -form, ми називаємо її функцією квадратного кореня. Оскільки ми бачимо, що існує одне обмеження на графік, де\(x\) значення починаються з початку і жодна частина графіка не знаходиться на лівій стороні походження, область цієї функції -\(\{x|x ≥ 0\}\) або\([0, ∞)\).
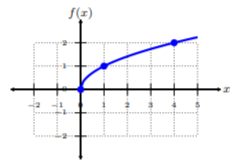
Графік\(f(x) =\sqrt[3]{x}\) і визначення домену.
Рішення
Давайте виберемо три\(x\) -координати, і знайдемо відповідні\(y\) -значення.
| \(x\) | \(f(x)=\sqrt[3]{x}\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-1\) | \ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{-1}\color{black}{})=-1\) | \ (x, f (x))\) ">\((-1,-1)\) |
| \ (x\) ">\(0\) | \ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{0}\color{black}{})=0\) | \ (x, f (x))\) ">\((0,0)\) |
| \ (x\) ">\(1\) | \ (f (x) =\ sqrt [3] {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x))\) ">\((1,1)\) |
Побудуйте замовлені-пари з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Ця функція виглядає як функція куба, але перевернута і\(90^{\circ}\) вправо! Ми називаємо цю функцію функцією кореня куба. Через корінь на радикалі. Оскільки ми бачимо, що немає обмежень на графік, домен - це всі дійсні числа або\((−∞, ∞)\).

Графік\(f(x) =\dfrac{1}{x}\) і визначення домену.
Рішення
Давайте виберемо\(x\) -координати, і знайдемо відповідні\(y\) -значення.
| \(x\) | \(f(x)=\dfrac{1}{x}\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-3\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-3}\color{black}{})=-\dfrac{1}{3}\) | \ (x, f (x))\) ">\((-3,-\dfrac{1}{3})\) |
| \ (x\) ">\(-2\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-2}\color{black}{})=-\dfrac{1}{2}\) | \ (x, f (x))\) ">\((-2,-\dfrac{1}{2})\) |
| \ (x\) ">\(-1\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{-1}\color{black}{})=-1\) | \ (x, f (x))\) ">\((-1,-1)\) |
| \ (x\) ">\(0\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{0}\color{black}{})=\text{undefined}\) | \ (x, f (x))\) ">немає точки |
| \ (x\) ">\(1\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{1}\color{black}{})=1\) | \ (x, f (x))\) ">\((1,1)\) |
| \ (x\) ">\(2\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{2}\color{black}{})=\dfrac{1}{2}\) | \ (x, f (x))\) ">\((2,\dfrac{1}{2})\) |
| \ (x\) ">\(3\) | \ (f (x) =\ dfrac {1} {x}\) ">\(f(\color{blue}{3}\color{black}{})=\dfrac{1}{3}\) | \ (x, f (x))\) ">\((3,\dfrac{1}{3})\) |
Побудуйте замовлені-пари з таблиці. Щоб з'єднати точки, обов'язково з'єднайте їх від найменшого\(x\) -значення до найбільшого\(x\) -значення, тобто зліва направо. Цей графік виглядає найбільш інакше, ніж інші функції, і це тому, що це дріб зі змінною в знаменнику. Нагадаємо, дроби не можуть мати нуль у своїх знаменниках, оскільки саме тоді дроби не визначені. Дізнаємося докладніше про ці функції, які називаються раціональними функціями. Наразі ми називаємо графік цієї функції зворотною функцією. Оскільки ми бачимо, що ця функція не може мати нуль у знаменнику, і, з таблиці, ми бачимо коли\(x = 0\), функція невизначена, то домен - це всі дійсні числа, крім\(x = 0: \{x|x \neq 0\}\) або\((−∞, 0) ∪ (0, ∞)\).

Бібліотека функцій Домашнє завдання
Нижче наведені графіки функцій.

Зіставте кожен граф з назвою його функції.
Назви функцій
- Взаємна функція
- Функція абсолютного значення
- Функція кореня куба
- Функція куба
- Постійна функція
- Функція ідентичності
- Функція квадратного кореня
- Квадратна функція
- Лінійна функція
Зіставте кожен графік з формулою функції.
Формули функцій
- \(f(x) = x\)
- \(f(x) = −4\)
- \(f(x) = |x|\)
- \(f(x) = x^2\)
- \(f(x) =\dfrac{1}{x}\)
- \(f(x) = x^3\)
- \(f(x) = mx + b\)
- \(f(x) =\sqrt[3]{x}\)
- \(f(x) =\sqrt{x}\)
Які домени для кожної з функцій?
