9.1: Вилучення квадратних коренів

Цілі навчання

• Розв'яжіть квадратні рівняння шляхом вилучення квадратних коренів.

Вилучення квадратних коренів

Нагадаємо, що квадратне рівняння знаходиться в стандартному вигляді, якщо воно дорівнює 0:

\[a x^{2}+b x+c=0\]

де a, b і c - дійсні числа і\(a\neq 0\). Рішення такого рівняння називається коренем. Квадратні рівняння можуть мати два дійсні розв'язки, одне дійсне рішення або відсутність реального розв'язку. Якщо квадратичний вираз на лівих факторах, то ми можемо вирішити його факторингом. Нижче наведено огляд кроків, які використовуються для вирішення факторингом:

Крок 1: Висловіть квадратне рівняння в стандартній формі.

Крок 2: Фактор квадратичного виразу.

Крок 3: Застосуйте властивість нульового продукту та встановіть кожен коефіцієнт змінної рівний 0.

Крок 4: Розв'яжіть отримані лінійні рівняння.

Наприклад, ми можемо вирішити\(x^{2}-4=0\) факторингом наступним чином:

\ (x+2) (x-2) &= 0\\ x+2 &=0\ quad\ текст {або}\ квад x-2 = 0\\ x &=-2\ quad\ quad\ quad\ quad\ :x = 2\ кінець {вирівняний}\) </p">

Два розв'язки: −2 та 2. Мета в цьому розділі - розробити альтернативний метод, який можна використовувати для легкого вирішення рівнянь, де b = 0, надаючи форму

\[a x^{2}+c=0\]

Рівняння\(x^{2}-4=0\) знаходиться в такому вигляді і може бути вирішено за допомогою першої ізоляції\(x^{2}\).

Якщо взяти квадратний корінь обох сторін цього рівняння, то отримаємо наступне:

\(\begin{aligned} \sqrt{x^{2}} &=\sqrt{4} \\|x| &=2 \end{aligned}\)

Тут ми бачимо, що\(x=-2\) і\(x=2\) є розв'язками отриманого рівняння. Загалом, це описує властивість квадратного кореня; для будь-якого дійсного числа k,

\[\text{If}\:x^{2}=k, \text { then } x=\pm \sqrt{k}\]

Позначення «±» читається «плюс або мінус» і використовується як компактне позначення, яке вказує на два рішення. Звідси твердження\(x=\pm \sqrt{k}\) вказує на те, що\(x= - \sqrt{k}\) або\(x= + \sqrt{k}\). Застосування властивості квадратного кореня як засобу вирішення квадратного рівняння називається вилученням коренів.

Приклад\(\PageIndex{1}\)

Вирішити:

\(x^{2}-25=0\)

Рішення:

Почніть з ізоляції квадрата.

Далі застосовуємо властивість квадратного кореня.

\(\begin{aligned} x^{2} &=25 \\ x &=\pm \sqrt{25} \\ x &=\pm 5 \end{aligned}\)

Відповідь:

Розв'язками є −5 і 5. Чек залишається на розсуд зчитувача.

Звичайно, попередній приклад міг би бути вирішений так само легко шляхом факторингу. Однак він демонструє методику, яка може бути використана для вирішення рівнянь у такій формі, які не враховують.

Приклад\(\PageIndex{2}\)

Вирішити:

\(x^{2}-5=0\)

Рішення:

Зверніть увагу, що квадратичний вираз зліва не фактор. Ми можемо витягти коріння, якщо спочатку виділимо провідний термін,\(x^{2}\).

Застосовуємо властивість квадратного кореня.

\(x=\pm \sqrt{5}\)

Для повноти перевірте, чи ці два реальні рішення вирішують вихідне квадратне рівняння. Як правило, перевірка необов'язкова.

\(\begin{array}{rlrl}{\text { Check } x=-\sqrt{5}} & {\text { Check } x=\sqrt{5}} \\ {x^{2}-5=0} & {x^{2}-5=0} \\ {(\color{OliveGreen}{-\sqrt{5}}\color{black}{)}^{2}-5=0} & {(\color{OliveGreen}{\sqrt{5}}\color{black}{)}^{2}-5=0} \\ {5-5=0} & {5-5=0} \\ {0=0 \color{Cerulean}{\checkmark}} & {0=0\color{Cerulean}{\checkmark}}\end{array}\)

Відповідь:
Рішення є\(-\sqrt{5}\) і\(\sqrt{5}\).

Приклад\(\PageIndex{3}\)

Вирішити

Рішення

Почніть з ізоляції\(x^{2}\).

Застосуйте властивість квадратного кореня, а потім спростіть.

\(\begin{array}{l}{x=\pm \sqrt{\frac{45}{4}}} \\ {x=\pm \frac{\sqrt{9 \cdot 5}}{\sqrt{4}}} \\ {x=\pm \frac{3 \sqrt{5}}{2}}\end{array}\)

Відповідь:

Рішення є\(-\frac{3 \sqrt{5}}{2}\) і\(\frac{3 \sqrt{5}}{2}\).

Іноді квадратні рівняння не мають реального рішення.

Приклад\(\PageIndex{4}\)

Вирішити:

\(x^{2} + 9 =0\)

Рішення

Почніть з ізоляції\(x^{2}\).

Після застосування властивості square root нам залишається квадратний корінь від'ємного числа. Тому реального рішення цього рівняння не існує.

Відповідь:

Немає реального рішення

Поверніть цей процес, щоб знайти рівняння із заданими розв'язками виду ±k.

Приклад\(\PageIndex{5}\)

Знайдіть рівняння з розв'язками\(-2 \sqrt{3}\) і\(2 \sqrt{3}\).

Рішення:

Почніть з квадрата обидві сторони наступного рівняння:

\(\begin{array}{l}{x=\pm 2 \sqrt{3}} \\ {x^{2}=( \pm 2 \sqrt{3})^{2}} \\ {x^{2}=4 \cdot 3} \\ {x^{2}=12}\end{array}\)

Нарешті, відніміть 12 з обох сторін і представите рівняння в стандартному вигляді.

Відповідь:

\(x^{2}-12=0\)

Вправа\(\PageIndex{1}\)

Вирішити:

\(9x^{2}-8=0\).

Відповідь

\(x=-\frac{2 \sqrt{2}}{3}\)або\(x=\frac{2 \sqrt{2}}{3}\)

Розглянемо рішення наступного рівняння:

\((x+2)^{2}=25\)

Щоб вирішити це рівняння факторингом, спочатку квадрат х+2, а потім поставити його в стандартному вигляді, рівному нулю, віднімаючи 25 з обох сторін.

Фактор, а потім застосувати властивість нульового добутку.

\(\begin{array}{c}{x^{2}+4 x-21=0} \\ {(x+7)(x-3)=0}\end{array}\)

\(\begin{array}{rr}{x+7=0} & {\text { or } \quad x-3=0} \\ {x=-7} & {x=3}\end{array}\)

Два рішення -7 і 3.

Коли рівняння знаходиться в такій формі, ми можемо отримати рішення за меншу кількість кроків, витягуючи коріння.

Приклад\(\PageIndex{6}\)

Вирішити:

\((x=2)^{2}=25\).

Рішення

Вирішити шляхом вилучення коренів.

\(\begin{array}{rlrr}{(x+2)^{2}} & {=25} & {\color{Cerulean}{ Apply\: the\:square \:root \:property.}} \\ {x+2} & {=\pm \sqrt{25}} & {\color{Cerulean}{ Simplify. }} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{array}\)

У цей момент розділіть «плюс або мінус» на два рівняння і спростіть кожне окремо.

\(\begin{array}{ll}{x=-2-5} & {\text { or } x=-2+5} \\ {x=-7} & {\quad\:\: x=3}\end{array}\)

Відповідь:

Рішення -7 і 3.

Крім меншої кількості кроків, цей метод дозволяє вирішувати рівняння, які не враховують фактор.

Приклад\(\PageIndex{7}\)

Вирішити:

\((3 x+3)^{2}-27=0\)

Рішення

Почніть з ізоляції квадрата.

\ (3 x+3) ^ {2} &=27\ end {вирівняний}\) </p">

Далі витягуємо коріння і спрощуємо.

\(\begin{aligned}(3 x+3)^{2} &=27 \\ 3 x+3 &=\pm \sqrt{27} \\ 3 x+3 &=\pm \sqrt{9 \cdot 3} \\ 3 x+3 &=\pm 3 \sqrt{3} \end{aligned}\)

Вирішити для х.

Відповідь:

Рішення є\(-1 - \sqrt{3}\) і\(-1 + \sqrt{3}\)

Приклад\(\PageIndex{8}\)

Вирішити:

\(9(2 x-1)^{2}-8=0\)

Рішення:

Почніть з виділення квадратного коефіцієнта.

\ (2 x-1) ^ {2} &=\ розрив {8} {9}\ end {вирівняний}\) </p">

Застосовуємо властивість квадратного кореня і вирішуємо.

Відповідь:

Рішення є\(\frac{3 - 2 \sqrt{2}}{6}\) і\(\frac{3 + 2 \sqrt{2}}{6}\)

Вправа\(\PageIndex{2}\)

Вирішити:

\(3(x-5)^{2}-2=0\)

Відповідь

\(15\pm 6\sqrt{3}\)

Приклад\(\PageIndex{9}\)

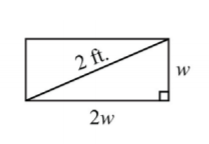
Довжина прямокутника в два рази більше ширини. Якщо діагональ вимірює 2 фути, то знайдіть розміри прямокутника.

Малюнок\(\PageIndex{1}\)

Рішення

Давайте уявляємо ширину.

Нехай 2w представляють довжину.

Діагональ будь-якого прямокутника утворює два прямих трикутника. Таким чином, застосовується теорема Піфагора. Сума квадратів катетів прямокутного трикутника дорівнює квадрату гіпотенузи:

\(\begin{array}{l}{(\operatorname{leg})^{2}+(\operatorname{leg})^{2}=\text { hypotenuse }^{2}} \\ {(\color{OliveGreen}{2 w}\color{black}{)}^{2}+(\color{OliveGreen}{w}\color{black}{)}^{2}=(\color{OliveGreen}{2}\color{black}{)}^{2}}\end{array}\)

Вирішити.

\(\begin{aligned}(2 w)^{2}+(w)^{2} &=(2)^{2} \\ 4 w^{2}+w^{2} &=4 \\ 5 w^{2} &=4 \quad\quad\quad\color{Cerulean}{Isolate\:w^{2}.} \\\frac{5w^{2}}{\color{Cerulean}{5}}&\color{black}{=}\frac{4}{\color{Cerulean}{5}}\\ w^{2}&=\frac{4}{5}\quad\:\:\quad\color{Cerulean}{Extract\:the\:roots.} \\ w&=\pm\sqrt{\frac{4}{5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)

Тут отримуємо два рішення,\(w=−\frac{2}{\sqrt{5}}\) і\(w=\frac{2}{\sqrt{5}}\). Оскільки проблема просила довжину прямокутника, ми нехтуємо негативною відповіддю. Крім того, ми раціоналізуємо знаменник і представимо наші рішення без будь-яких радикалів у знаменнику.

\(\begin{aligned} w &=\frac{2}{\sqrt{5}} \quad\quad\quad\quad\color{Cerulean}{Rationalize\:the\:denominator.} \\ &=\frac{2}{\sqrt{5}} \cdot \color{Cerulean}{\frac{\sqrt{5}}{\sqrt{5}}} \\ &=\frac{2 \sqrt{5}}{\sqrt{25}} \\ &=\frac{2 \sqrt{5}}{5} \end{aligned}\)

Назад підставляємо, щоб знайти довжину.

\(\begin{aligned} l &=2 w \\ &=2\color{black}{\left(\color{OliveGreen}{\frac{2 \sqrt{5}}{5}}\right)} \\ &=\frac{4 \sqrt{5}}{5} \end{aligned}\)

Відповідь:

Довжина прямокутника -\(\frac{4 \sqrt{5}}{5}\) фути, а ширина -\(\frac{2 \sqrt{5}}{5}\) фути.

Ключові виноси

• Вирішити рівняння форми\(ax^{2}+c=0\) шляхом вилучення коренів.
• Вилучення коренів передбачає ізоляцію квадрата, а потім застосування властивості квадратного кореня. Після застосування властивості квадратного кореня у вас є два лінійних рівняння, кожне з яких може бути розв'язано. Обов'язково спростіть всі радикальні вирази і раціоналізуйте знаменник при необхідності.

Вправа\(\PageIndex{3}\) extracting square roots

Вирішити шляхом факторингу, а потім вирішити шляхом вилучення коренів. Перевірте відповіді.

1. \(x^{2}-36=0\)
2. \(x^{2}-81=0\)
3. \(4y^{2}−9=0\)
4. \(9y^{2}−25=0\)
5. \((x−2)^{2}−1=0\)
6. \((x+1)^{2}−4=0\)
7. \(4(y−2)^{2}−9=0\)
8. \(9(y+1)^{2}−4=0\)
9. \(−3(t−1)^{2}+12=0\)
10. \(−2(t+1)^{2}+8=0\)
11. \((x−5)^{2}−25=0\)
12. \((x+2)^{2}−4=0\)

Відповідь

1. \(-6, 6\)

3. \(-\frac{3}{2} , \frac{3}{2}\)

5. \(1, 3\)

7. \(\frac{1}{2}, \frac{7}{2}\)

9. \(-1, 3\)

11. \(0, 10\)

Вправа\(\PageIndex{4}\) extracting square roots

Вирішити шляхом вилучення коренів.

1. \(x^{2}=16\)
2. \(x^{2}=1\)
3. \(y^{2}=9\)
4. \(y^{2}=64\)
5. \(x^{2}=14\)
6. \(x^{2}=19\)
7. \(y^{2}=0.25\)
8. \(y^{2}=0.04\)
9. \(x^{2}=12\)
10. \(x^{2}=18\)
11. \(16x^{2}=9\)
12. \(4x^{2}=25\)
13. \(2t^{2} = 1\)
14. \(3t^{2} = 2\)
15. \(x^{2} −100 = 0\)
16. \(x^{2} −121 = 0\)
17. \(y^{2} + 4 = 0\)
18. \(y^{2} + 1 = 0\)
19. \(x^{2} −49 = 0\)
20. \(x^{2} −925 = 0\)
21. \(y^{2} −0.09 = 0\)
22. \(y^{2} −0.81 = 0\)
23. \(x^{2} − 7 = 0\)
24. \(x^{2} − 2 = 0\)
25. \(x^{2} − 8 = 0\)
26. \(t^{2} −18 = 0\)
27. \(x^{2} + 8 = 0\)
28. \(x^{2} +125 = 0\)
29. \(16x^{2} −27 = 0\)
30. \(9x^{2} − 8 = 0\)
31. \(2y^{2} − 3 = 0\)
32. \(5y^{2} − 2 = 0\)
33. \(3x^{2} − 1 = 0\)
34. \(6x^{2} − 3 = 0\)
35. \((x + 7 )^{2} − 4 = 0\)
36. \((x + 9 )^{2} −36 = 0\)
37. \(( 2y − 3 )^{2} −81 = 0 \)
38. \(( 2y + 1 )^{2} −25 = 0\)
39. \((x − 5 )^{2} −20 = 0\)
40. \((x + 1 )^{2} −28 = 0\)
41. \(( 3t + 2 )^{2} − 6 = 0\)
42. \((3t−5)^{2}−10=0\)
43. \(4(y+2)^{2}−3=0\)
44. \(9(y−7)^{2}−5=0\)
45. \(4(3x+1)^{2}−27=0\)
46. \(9(2x−3)^{2}−8=0\)
47. \(2(3x−1)^{2}+3=0\)
48. \(5(2x−1)^{2}−3=0\)
49. \(3(y−23)^{2}−32=0\)
50. \(2(3y−13)^{2}−52=0\)

Відповідь

1. ± 4

3. ± 3

5. ±\(\frac{1}{2}\)

7. ± 0,5

9. ±\(2\sqrt{3}\)

11. ±\(\frac{3}{4}\)

13. ±\(\sqrt{\frac{1}{2}}\)

15. ± 10

17. Немає реального рішення

19. ±\(\frac{2}{3}\)

21. ± 0,3

23. ±\(\sqrt{7}\)

25. ±\(2\sqrt{2}\)

27. Немає реального рішення

29. ±\(\frac{3 \sqrt{3}}{4}\)

31. ±\(6\sqrt{2}\)

33. ±\(3\sqrt{3}\)

35. \(−9, −5\)

37. \(−3, 6\)

39. \(5\)±\(2\sqrt{5}\)

41. ±\(\frac{\sqrt{6}-2}{3}\)

43. ±\(\frac{\sqrt{3}}{2}-2\)

45. ±\(\frac{3 \sqrt{3}-2}{6}\)

47. Немає реального рішення

49. ±\(\frac{4 \sqrt{6}}{3}+23\)

Вправа\(\PageIndex{5}\) extracting square roots

Знайдіть квадратне рівняння в стандартній формі з наступними розв'язками.

1. ±7
2. ± 13
3. ±\(\sqrt{7}\)
4. ±\(\sqrt{3}\)
5. ±\(3\sqrt{5}\)
6. ±\(5\sqrt{2}\)
7. \(1\)±\(\sqrt{2}\)
8. \(2\)±\(\sqrt{3}\)

Відповідь

1. \(x^{2}−49=0\)

3. \(x^{2}−7=0\)

5. \(x^{2}−45=0\)

7. \(x^{2}−2x−1=0\)

Вправа\(\PageIndex{6}\) extracting square roots

Вирішіть і округляйте рішення до сотих.

1. \(9x(x+2)=18x+1\)
2. \(x^{2}=10(x^{2}−2)−5\)
3. \((x+3)(x−7)=11−4x\)
4. \((x−4)(x−3)=66−7x\)
5. \((x−2)^{2}=67−4x\)
6. \((x+3)^{2}=6x+59\)
7. \((2x+1)(x+3)−(x+7)=(x+3)^{2}\)
8. \((3x−1)(x+4)=2x(x+6)−(x−3)\)

Відповідь

1. ± 0,33

3. ± 5,66

5. ± 7,94

7. ± 3,61

Вправа\(\PageIndex{7}\) extracting square roots

Налаштуйте алгебраїчне рівняння і використовуйте його для вирішення наступного.

1. Якщо з 4 разів віднімається 9 квадрат числа, то результат дорівнює 3. Знайдіть номер.
2. Якщо з квадрата числа віднімається 20, то результат дорівнює 4. Знайдіть номер.
3. Якщо 1 додається в 3 рази більше квадрата числа, то результат дорівнює 2. Знайдіть номер.
4. Якщо 3 додати в 2 рази квадрат числа, то результат дорівнює 12. Знайдіть номер.
5. Якщо квадрат має площу 8 квадратних сантиметрів, то знайдіть довжину кожної сторони.
6. Якщо коло має площу 32\(\pi\) квадратних сантиметри, то знайдіть довжину радіуса.
7. Обсяг правого круглого конуса становить 36\(\pi\) кубічних сантиметрів при висоті 6 сантиметрів. Знайдіть радіус конуса. (Обсяг правого кругового конуса задається за допомогою\(V=13\pi r^{2}h\).)
8. Площа поверхні кулі становить 75\(\pi\) квадратних сантиметрів. Знайдіть радіус сфери. (Площа поверхні сфери задається SA=\(4\pi r^{2}\).)
9. Довжина прямокутника в 6 разів більше його ширини. Якщо площа становить 96 квадратних дюймів, то знайдіть розміри прямокутника.
10. Підстава трикутника в два рази більше висоти. Якщо площа становить 16 квадратних сантиметрів, то знайдіть довжину його підстави.
11. Квадрат має площу 36 квадратних одиниць. На яку рівну величину доведеться збільшити сторони, щоб створити квадрат з подвоєною заданою площею?
12. Коло має площу 25\(\pi\) квадратних одиниць. На яку величину радіус доведеться збільшити, щоб створити коло з подвоєною заданою площею?
13. Якщо сторони квадрата відміряють 1 одиницю, то знайдіть довжину діагоналі.
14. Якщо сторони квадрата вимірюють 2 одиниці, то знайдіть довжину діагоналі.
15. Діагональ квадрата вимірює 5 дюймів. Знайдіть довжину кожної сторони.
16. Діагональ квадрата вимірює 3 дюйми. Знайдіть довжину кожної сторони.
17. Довжина прямокутника в два рази більше ширини. Якщо діагональ вимірює 10 футів, то знайдіть розміри прямокутника.
18. Довжина прямокутника в два рази більше ширини. Якщо діагональ вимірює 8 футів, то знайдіть розміри прямокутника.
19. Довжина прямокутника в 3 рази більше його ширини. Якщо діагональ вимірює 5 метрів, то знайдіть розміри прямокутника.
20. Довжина прямокутника в 3 рази більше його ширини. Якщо діагональ вимірює 2 фути, то знайдіть розміри прямокутника.
21. Висота в футах об'єкта, опущеного з 9-футової сходи, задається h (t)\(=−16t^{2}+9\), де t представляє час у секундах після скидання об'єкта. Скільки часу потрібно об'єкту, щоб вдаритися об землю? (Підказка: висота дорівнює 0, коли об'єкт потрапляє на землю.)
22. Висота в футах об'єкта, скинутого з 20-футової платформи, задається h (t)\(=−16t^{2}+20\), де t представляє час у секундах після скидання об'єкта. Скільки часу потрібно об'єкту, щоб вдаритися об землю?
23. Висота в футах об'єкта, опущеного з вершини 144-футової будівлі, задається h (t)\(=−16t^{2}+144\), де t вимірюється в секундах.
    1. Скільки часу знадобиться, щоб досягти половини відстані до землі, 72 футів?
    2. Скільки часу знадобиться, щоб проїхати решту відстані до землі? Округлити до найближчої сотої частки секунди.
24. Висота в футах об'єкта, скинутого з літака на 1600 футів, задається h (t)\(=−16t^{2}+1,600\), де t знаходиться в секундах.
    1. Скільки часу знадобиться, щоб досягти половини відстані до землі?
    2. Скільки часу знадобиться, щоб проїхати решту відстані до землі? Округлити до найближчої сотої частки секунди.
25. Створіть власне рівняння, яке можна вирішити шляхом вилучення кореня. Поділіться ним разом з рішенням на дошці обговорень.
26. Поясніть, чому техніка вилучення коренів значно розширює нашу здатність вирішувати квадратичні рівняння.
27. Поясніть своїми словами, як вирішити шляхом вилучення коренів 106. Вивести формулу діагоналі квадрата через його сторони.

Відповідь

1. \(−\sqrt{3}\)або\(\sqrt{3}\)

3. \(−3\sqrt{3}\)або\(3\sqrt{3}\)

5. \(2\sqrt{2}\)сантиметри

7. \(3\sqrt{2}\)сантиметри

9. Довжина: 24 дюйма; ширина: 4 дюйми

11. \(−6+6\sqrt{2}\approx 2.49\)одиниць

13. \(\sqrt{2}\)одиниць

15. \(52\sqrt{2}\)дюймів

17. Довжина:\(4\sqrt{5}\) стопи; ширина:\(2\sqrt{5}\) стопи

19. Довжина:\(310−−\sqrt{2}\) метри; ширина:\(10−−\sqrt{2}\) метри

21. \(\frac{3}{4}\)другий

23. а. 2,12 секунди б. 0,88 секунди

25. Відповіді можуть відрізнятися