Skip to main content
LibreTexts - Ukrayinska

2.5: Додатки

  1. Last updated
  2. Save as PDF
  • Page ID
    58187

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Рішення проблеми слова повинно включати в себе кожен з наступних кроків.

    Вимоги до вирішення проблем Word

    1. Налаштуйте словник змінних. Ви повинні повідомити своїм читачам, що представляє кожна змінна у вашій проблемі. Це може бути досягнуто кількома способами:
      • Такі заяви, як «\(P\)Дозволяти представляти периметр прямокутника».
      • Позначення невідомих значень змінними в таблиці.
      • Маркування невідомих величин в ескізі або схемі.
    2. Налаштуйте рівняння.Кожне рішення проблеми зі словом має містити ретельно розроблене рівняння, яке точно описує обмеження в постановці задачі.
    3. Розв'яжіть рівняння. Ви завжди повинні вирішувати рівняння, встановлене на попередньому кроці.
    4. Дайте відповідь на питання. Цей крок легко не помітити. Наприклад, проблема може запитати вік Джейн, але рішення вашого рівняння дає вік сестри Джейн Ліз. Переконайтеся, що ви відповіли на оригінальне запитання, поставлене в проблемі. Ваше рішення має бути записано в реченні з відповідними одиницями.
    5. Озирніться назад. Важливо зазначити, що цей крок не означає, що ви повинні просто перевірити своє рішення у своєму рівнянні. Зрештою, можливо, ваше рівняння неправильно моделює ситуацію задачі, тож ви можете мати правильне рішення неправильного рівняння. Важливе питання: «Чи має сенс ваша відповідь на основі слів в оригінальній постановці проблеми».

    Давайте наведемо цим вимогам тест-драйв.

    Приклад\(\PageIndex{1}\)

    У три більше п'яти разів є певним числом\(-62\). Знайдіть номер.

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. \(x\)Дозволяти представляти невідоме число.
    2. Налаштуйте рівняння. «У три більше п'яти разів певне число є\(-62\)» стає:

    рис. 2.5.1a.png

    1. Розв'яжіть рівняння. Щоб вирішити для\(x\), спочатку відніміть\(3\) з обох сторін рівняння. \[\begin{aligned} 3+5 x &= -62 \quad \color {Red} \text { Original equation. } \\ 3+5 x-3 &= -62-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides. } \\ 5x &= -65 \quad \color {Red} \text { Simplify. } \\ \dfrac{5 x}{5} &= \dfrac{-65}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ x &= -13 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    2. Дайте відповідь на питання. Невідомий номер є\(-13\).
    3. Озирніться назад. Обчислити «три більше п'яти разів»\(-13\). \[\begin{aligned} 3+5(-13) &=3+(-65) \\ &=-62 \end{aligned} \nonumber \]Отже, три більше п'яти разів\(-13\)\(-62\), як потрібно. Наше рішення правильне.

    Вправа\(\PageIndex{1}\)

    \(27\) more than \(5\) times a certain number is \(-148\). What is the number?

    Відповідь

    \(-35\)

    Приклад\(\PageIndex{2}\)

    Сума трьох послідовних цілих чисел дорівнює\(-66\). Знайдіть найменше з цих трьох цілих чисел.

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. \(k\)Дозволяти представляти найменше з трьох послідовних цілих чисел.
    2. Налаштуйте рівняння. Приклад трьох послідовних цілих чисел -\(34\)\(35\), і\(36\). Це не цілі числа, які ми шукаємо, але вони служать для допомоги в розумінні проблеми. Зверніть увагу, що кожне послідовне ціле число на одне більше, ніж попереднє ціле число. Якщо\(k\) є найменшим з трьох послідовних цілих чисел, то наступні два послідовних цілих числа -\(k +1\) і\(k +2\). «Сума трьох послідовних цілих чисел є\(-66\)» стає:

    рис. 2.5.1b.png

    1. Розв'яжіть рівняння. Щоб вирішити для\(k\), спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} k+(k+1)+(k+2) &=-66 \quad \color {Red} \text { Original equation. }\\ 3k+3 &=-66 \quad \color {Red} \text { Combine like terms. }\\ 3k+3-3 &=-66-3 \quad \color {Red} \text { Subtract } 3 \text { from both sides.}\\ 3k &=-69 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{-69}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=-23 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    2. Дайте відповідь на питання. Найменше з трьох послідовних цілих чисел -\(-23\).
    3. Озирніться назад. Якщо\(k = -23\) є найменшим з трьох послідовних цілих чисел, то наступні два послідовних цілих числа -\(-22\) і\(-21\). Давайте перевіримо суму цих трьох послідовних цілих чисел. \[-23+(-22)+(-21)=-66 \nonumber \]Отже, сума трьох послідовних цілих чисел дорівнює\(-66\), як потрібно. Наше рішення правильне

    Вправа\(\PageIndex{2}\)

    Сума трьох послідовних непарних цілих чисел дорівнює\(-225\). What are the integers?

    Відповідь

    \(-77,-75,-73\)

    Приклад\(\PageIndex{3}\)

    Тесляр вирізає дошку розміром\(60\) дюймів на три частини. Другий шматок вдвічі довший, ніж перший шматок, а третій шматок втричі довший, ніж перший шматок. Знайдіть довжину кожного шматка, відрізаного столяром.

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. \(L\)Дозволяти представляти довжину першого шматка. Потім другий шматок, який вдвічі довший за перший шматок, має довжину\(2L\). Третій шматок, який в три рази довший, ніж перший шматок, має довжину\(3L\). Давайте побудуємо невелику таблицю, яка допоможе узагальнити інформацію, надану в цій задачі.
    Шматок Довжина (в)
    Перший шматок Л
    Другий шматок 2Л
    Третій шматок 3Л
    Загальна довжина 60
    1. Налаштуйте рівняння. Як ви можете бачити в таблиці вище, другий стовпець показує, що сума трьох штук дорівнює\(60\) дюймам. В символах:\[L+2 L+3 L=60 \nonumber \]
    2. Розв'яжіть рівняння. Щоб вирішити для\(L\), спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} L+2 L+3 L &= 60 \quad \color {Red} \text { Original equation. } \\ 6L &= 60 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{6L}{6} &= \dfrac{60}{6} \quad \color {Red} \text { Divide both sides by } 6 \\ L &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    3. Дайте відповідь на питання. Перший шматок має довжину L = 10 дюймів. Другий шматок має довжину 2L = 20 дюймів. Третій шматок має довжину 3L = 30 дюймів. У табличній формі це ще більш очевидно.
    Шматок Довжина (в) Довжина (в)
    Перший шматок Л 10
    Другий шматок 2Л 20
    Третій шматок 3Л 30
    Загальна довжина 60 60
    1. Озирніться назад. Друга довжина не тільки вдвічі перевищує першу, а третю довжину втричі більше першої, перевірте суму їх довжин:\[10+20+30=60 \nonumber \] Це загальна кількість\(60\) дюймів. У нас є правильне рішення.

    Вправа\(\PageIndex{3}\)

    Хан вирізає дошку\(230\) inches in three pieces. The second piece is twice as long as the , вимірюючи перший шматок, а третій шматок\(30\) inches longer than the second piece. Find the length of each piece cut by Han.

    Відповідь

    \(40,80,110\)в

    Приклад\(\PageIndex{4}\)

    Три сторони трикутника є послідовними парними цілими числами. Якщо периметр (сума трьох сторін) трикутника дорівнює\(156\) сантиметрам, знайдіть довжину кожної сторони трикутника.

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. Приклад трьох послідовних парних цілих чисел -\(18\)\(20\), і\(22\). Це не цілі числа, які ми шукаємо, але вони дають нам деяке відчуття значення трьох послідовних парних чисел. Зверніть увагу, що кожне послідовне парне ціле число на два більше, ніж попереднє ціле число. Таким чином\(k\), якщо довжина першої сторони трикутника, то наступні дві сторони -\(k+2\) і\(k+4\). У цьому прикладі наш словник змінних буде мати форму добре позначеної фігури.

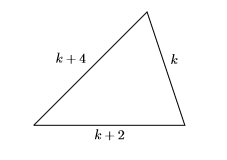
    рис. 2.5.1c.png

    1. Налаштуйте рівняння. Периметр трикутника - це сума трьох сторін. Якщо периметр дорівнює\(156\) сантиметрам, то:\[k+(k+2)+(k+4)=156 \nonumber \]
    2. Розв'яжіть рівняння. Щоб розв'язати для k, спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} k+(k+2)+(k+4) &=156 \quad \color {Red} \text { Original equation. }\\ 3k+6 &=156 \quad \color {Red} \text { Combine like terms. }\\ 3k+6-6 &=156-6 \quad \color {Red} \text { Subtract } 6 \text { from both sides.}\\ 3k &=150 \quad \color {Red} \text { Simplify. }\\ \dfrac{3k}{3} &=\dfrac{150}{3} \quad \color {Red} \text { Divide both sides by } 3.\\ k &=50 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    3. Дайте відповідь на питання. Таким чином, перша сторона має довжину\(50\) сантиметри. Тому що наступні два послідовних парних цілих числа\(k+2=52\) і\(k+4= 54\), три сторони трикутника вимірюють\(50\)\(52\), і\(54\) сантиметри, відповідно.
    4. Озирніться назад. Зображення допомагає нашому розумінню. Три сторони є послідовними парними цілими числами.

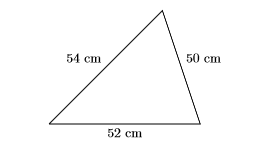
    рис. 2.5.1d.png

    Зверніть увагу, що периметр (сума трьох сторін) дорівнює:\[50 \mathrm{cm}+52 \mathrm{cm}+54 \mathrm{cm}=156 \mathrm{cm} \nonumber \] Таким чином, периметр дорівнює\(156\) сантиметрам, як і належить. Наше рішення правильне.

    Вправа\(\PageIndex{4}\)

    Три сторони трикутника є послідовними цілими числами. Якщо периметр (сума трьох сторін) трикутника\(453\) centimeters, знайти довжину кожної сторони трикутника.

    Відповідь

    \(150,151,152 \)см

    Приклад\(\PageIndex{5}\)

    Відомим фактом з геометрії є той факт, що сума кутів трикутника дорівнює\(180^{\circ}\). Припустимо, у нас є трикутник, другий кут якого на\(10\) градуси більше, ніж удвічі більше першого кута, і третій кут якого на\(50\) градуси більший за його перший кут. Знайдіть міру кожного кута трикутника.

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. Грецький алфавіт починається з букв\(\alpha, \beta, \gamma, \delta, \epsilon, \ldots,\) приблизно так само, як англійський алфавіт починається з букв\(a, b, c, d, e, \ldots\) Математики люблять використовувати грецькі літери, особливо при вивченні тригонометрії. Грецька буква\(\theta\) (вимовляється «тета») особливо прихильна у представленні кута трикутника. Отже, ми дозволимо\(\theta\) представляти градусну міру першого кута трикутника. Другий кут на\(10\) градуси більше, ніж удвічі перший кут, тому другий кут є\(2\theta+10\). Третій кут на\(50\) градуси більше першого кута, тому третій кут є\(\theta+50\). Знову ж таки, ми створимо добре позначену фігуру для нашого змінного словника.

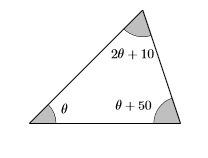
    рис. 2.5.1e.png

    1. Налаштуйте рівняння. Сума кутів дорівнює\(180^{\circ}\), так:\[\theta+(2 \theta+10)+(\theta+50)=180 \nonumber \]
    2. Розв'яжіть рівняння. Щоб вирішити для\(\theta\), спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} \theta+(2 \theta+10)+(\theta+50) & =180 \quad \color {Red} \text { Original equation. }\\ 4 \theta+60 & =180 \quad \color {Red} \text { Combine like terms. }\\ 4 \theta+60-60 & =180-60 \quad \color {Red} \text { Subtract } 60 \text { from both sides.}\\ 4 \theta & =120 \quad \color {Red} \text { Simplify. }\\ \dfrac{4 \theta}{4} & =\dfrac{120}{4} \quad \color {Red} \text { Divide both sides by } 4.\\ \theta & =30 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    3. Дайте відповідь на питання. Таким чином, перший кут -\(\theta=30\) градуси, другий -\(2\theta+10=70\) градуси, а третій -\(\theta+50=80\) градуси.
    4. Озирніться назад. Зображення допомагає нашому розумінню. Зверніть увагу, що другий кут на 10 градусів більше, ніж удвічі більший перший кут. Зверніть увагу, що третій кут на\(50\) градуси більше першого кута.

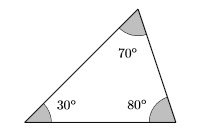
    рис. 2.5.1f.png

    Зверніть увагу, що сума кутів така:\[30^{\circ}+70^{\circ}+80^{\circ}=180^{\circ} \nonumber \] Таким чином, сума трьох кутів становить 180 градусів, як і повинно бути. У нас є правильне рішення.

    Вправа\(\PageIndex{5}\)

    Другий кут трикутника в три рази більше першого кута. Третій кут трикутника - це\(40\) degrees larger than the second angle. How many degrees are in each angle?

    Відповідь

    \(20^{\circ}, 60^{\circ}, 100^{\circ}\)

    Приклад\(\PageIndex{6}\)

    Марта успадковує\(\$21,000\) і вирішує вкласти гроші на три окремих рахунки. Сума, яку вона інвестує на другий рахунок, вдвічі перевищує суму, яку вона інвестує на перший рахунок. Сума, яку вона вкладає на третій рахунок,\(\$1,000\) більше суми, яку вона вкладає на другий рахунок. Скільки вона вклала в кожен рахунок?

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. Ми будемо використовувати таблицю в цьому прикладі, щоб допомогти налаштувати наш змінний словник. Нехай\(x\) буде сума, вкладена на перший рахунок. Сума, вкладена на другий рахунок, вдвічі більше, ніж вкладена в перший рахунок,\(2x\) так само і сума, вкладена в другий рахунок. Інвестиція третього рахунку\(\$1,000\) більше, ніж сума, вкладена на другий рахунок, так що є\(2x + 1000\).
    Обліковий запис # Сума інвестування
    Рахунок #1 х
    Рахунок #2 2х
    Рахунок #3 2х+1000
    Всього інвестовано 21000
    1. Налаштуйте рівняння. Другий стовпець таблиці розкриває необхідне рівняння. Три інвестиції повинні скласти\(\$21,000\). \[x+2 x+(2 x+1000)=21000 \nonumber \]
    2. Розв'яжіть рівняння. Щоб вирішити для\(x\), спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} x+2 x+(2 x+1000) &=21000 \quad \color {Red} \text { Original equation. }\\ 5 x+1000 &=21000 \quad \color {Red} \text { Combine like terms. }\\ 5 x+1000-1000 &=21000-1000 \quad \color {Red} \text { Subtract } 1000 \text { from both sides.}\\ 5 x &=20000 \quad \color {Red} \text { Simplify. }\\ \dfrac{5 x}{5} &=\dfrac{20000}{5} \quad \color {Red} \text { Divide both sides by } 5.\\ x &=4000 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    3. Дайте відповідь на питання. \(x = 4000\)Підставте в кожному записі другого стовпця таблиці вище, щоб отримати результати в таблиці нижче.
    Обліковий запис # Сума інвестування Сума інвестування
    Рахунок #1 х $4,000
    Рахунок #2 2х $8,000
    Рахунок #3 2х+1000 $9,000
    Всього інвестовано 21000 $21 000
    1. Озирніться назад. Як ми бачимо в нашій таблиці відповідей, сума,\(\$8,000\) вкладена на другий рахунок, вдвічі перевищує суму, вкладену в перший рахунок. Сума,\(\$9,000\) вкладена на третій рахунок,\(\$1,000\) більше суми, вкладеної на другий рахунок. Більше того, загальна сума інвестицій становить:\[\$ 4,000+\$ 8,000+\$ 9,000=\$ 21,000 \nonumber \] Таким чином, загальна сума інвестицій\(\$21,000\), як і належить. У нас є правильне рішення.

    Вправа\(\PageIndex{6}\)

    Джим успадковує\(\$15,000\). He invests part in a fund that pays \(5\%\) per year and the rest in a fund that pays \(4\%\) per year. At the end of one year, the combined interest from both investments was \(\$4,250\). How much did he invest in each fund?

    Відповідь

    \(\$ 5,000\)в\(5\%\) і\(\$ 10,000\) в\(4\% \).

    Приклад\(\PageIndex{7}\)

    Je- це\(2,650\) піші прогулянки по Тихоокеанському гребеню стежки з Мексики до Канади. Незадовго до того, як він перетинається з Орегону до Вашингтона, він знаходиться в чотири рази далі від початку стежки, ніж від кінця. Скільки далі йому доведеться походити?

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. \(d\)Дозволяти представляти відстань, що залишилася для Jeдля походу. Оскільки Jeзнаходиться в чотири рази далі від початку стежки, ніж кінець, відстань Jeвже завершена\(4d\). Давайте побудуємо невелику таблицю, яка допоможе узагальнити інформацію, надану в цій задачі.
    Розділ стежки Відстань (миль)
    Відстань до фінішу d
    Відстань від старту 4d
    Загальна відстань 2650
    1. Налаштуйте рівняння. Як ви можете бачити в таблиці вище, другий стовпець показує, що сума двох відстаней становить\(2650\) милі. У символах:\ [d+4 d=2650\ nonчисло\
    2. Розв'яжіть рівняння. Щоб вирішити для\(d\), спочатку спростіть ліву частину рівняння, об'єднавши подібні терміни. \[\begin{aligned} d+4d & =2650 \quad \color {Red} \text { Original equation. } \\ 5d & =2650 \quad \color {Red} \text { Combine like terms. } \\ \dfrac{5d}{5} & =\dfrac{2650}{5} \quad \color {Red} \text { Divide both sides by } 5 \\ d & =530 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    3. Дайте відповідь на питання. Jeще має\(530\) милі для походу.
    4. Озирніться назад. Оскільки сума, що залишилася для походу, становить\(d = 530\) милі, відстань Jeвід початку стежки становить\(4d = 4(530)\), або\(2,120\) милі. Якщо розташувати ці результати в табличній формі, то очевидно, що відстань від початку стежки не тільки в чотири рази перевищує відстань, що залишилася до фінішу, але й сума їх довжин дорівнює загальній довжині стежки.
    Розділ стежки Відстань (миль) Відстань (миль)
    Відстань до фінішу d 530
    Відстань від старту 4d 2120
    Загальна відстань 2650 2650

    Таким чином, ми маємо правильне рішення.

    Вправа\(\PageIndex{7}\)

    Маргарет їде на велосипеді по смузі, яка вимірює\(100\) miles. If Магарет в чотири рази далі від початку їзди, як вона від фінішу, скільки ще миль їй доведеться пройти, перш ніж вона закінчить свою поїздку?

    Відповідь

    \(20\)миль

    Приклад\(\PageIndex{8}\)

    Сьогодні\(15\%\) сестри Дамаріс сьомого класу захворіли і залишилися вдома зі школи. Якщо присутні лише\(34\) учні, який фактичний розмір класу сестри Дамаріс?

    Рішення

    У рішенні розглядаємо кожен крок Вимоги до вирішення проблем Word.

    1. Налаштуйте словник змінних. \(S\)Дозволяти представляти фактичний розмір класу Сестри Дамаріс.
    2. Налаштуйте рівняння. Якщо клас\(15\%\) сестри Дамаріс був відсутній, значить,\(85\%\) в її класі був присутній. Є\(34\) студент присутній, так що фраза «\(85\%\)класу сестри Дамаріс\(34\)» перекладається в рівняння,\[0.85 S=34 \nonumber \] де ми\(85\%\) змінили десяткову, перемістивши десяткову крапку на два розряди вліво.
    3. Розв'яжіть рівняння. Щоб вирішити для\(S\), спочатку очистіть десяткові числа, помноживши обидві сторони рівняння на\(100\). \[\begin{aligned} 0.85S &= 34 \quad \color {Red} \text { Original equation. } \\ 85S &= 3400 \quad \color {Red} \text { Multiply both sides by } 100. \\ \dfrac{85S}{85}&= \dfrac{3400}{85} \quad \color {Red} \text { Divide both sides by } 85 \\ S&= 40 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]
    4. Дайте відповідь на питання. Розмір класу сестри Дамаріс є\(40\).
    5. Озирніться назад. Нам сказали, що\(15\%\) клас сестри Дамаріс відсутній. Якщо підрахувати\(15\%\)\(40\), то отримаємо:\[0.15(40)=6 \nonumber \] Таким чином, було 6 студентів відсутні, значить\(40-6\), або\(34\) студенти були присутні. Таким чином, ми маємо правильне рішення.

    Вправа\(\PageIndex{8}\)

    \(20\%\)класу Марії хворіли і залишилися вдома зі школи. Якщо тільки\(36\) students are present, what is the actual size of Mary’s class?

    Відповідь

    \(45\)