2.4: Формули

Last updated
Save as PDF

Page ID: 58200

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Формули науки зазвичай містять змінні літери, крім змінної «Formulae» є множиною для «формули». x. Дійсно, формули в науці зазвичай використовують кілька букв. Наприклад, Загальний закон тяжіння Ісаака Ньютона говорить про те, що величина сили тяжіння між двома небесними тілами задається формулою:

\[F=\frac{G M m}{r^{2}} \nonumber \]

де$m$ зазвичай позначається маса меншого тіла,$M$ маса більшого тіла, і$r$ це відстань між двома тілами. Буква$G$ являє собою універсальну гравітаційну константу, що має значення$6.67428×10^{-11}$$N(m/kg)^2$.

Змінний випадок

Зверніть увагу на використання верхньої та нижньої літери M у законі гравітації Ньютона. При роботі з науковими формулами ви повинні підтримувати регістр заданих букв. Ви не можете замінювати нижній регістр на верхній регістр або верхній для нижнього регістру у вашій роботі.

У розділі 2.2 ми описали мету, яка повинна бути досягнута, коли нас попросять «вирішити рівняння для"$x$.

Вирішити для$x$

Коли його просять вирішити рівняння для$x$, мета полягає в тому, щоб маніпулювати рівнянням у кінцевій формі

\[x=\text {“Stuff”} \nonumber \]
де «Stu» є дійсним математичним виразом, яке може містити інші змінні, математичні символи тощо, але воно не повинно містити жодного входження змінної$x$.

Таким чином, щоб вирішити рівняння для$x$, нам потрібно виділити члени, що містять з одного$x$ боку рівняння, а всі залишилися члени з іншого боку рівняння.

Приклад$\PageIndex{1}$

Вирішити для$x : x+a=b$.

Рішення

Щоб скасувати ефекти додавання a, відніміть a з обох сторін рівняння.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-a &= b-a \quad \color{Red} \text { Subtract } a \text { from both sides. } \\ x &= b-a \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Вправа$\PageIndex{1}$

Вирішити для$x : x-c=d$.

Відповідь: $x=c+d$

У прикладі зверніть увагу$\PageIndex{1}$, що відповідь$x = b−a$ має необхідну форму$x = \text {“Stuff”}$, де «Stu» є дійсним математичним виразом, що містить інші змінні, математичні символи тощо, але воно не містить жодного входження змінної$x$. Що робити, якщо нас попросять вирішити те саме рівняння для$a$, а не$x$?

Приклад$\PageIndex{2}$

Вирішити для$a : x+a=b$.

Рішення

Нам доручено вирішити рівняння$x+a = b$ для$a$. Це означає, що наша кінцева відповідь повинна мати вигляд$a = \text {“Stuff”}$, де «Stu» є дійсним математичним виразом, що містить інші змінні, математичні символи тощо, але воно не містить жодного входження змінної$a$. Це означає, що ми повинні ізолювати всі члени, що містять змінну з одного$a$ боку рівняння, а всі інші члени на іншій стороні рівняння. Тепер, щоб скасувати ефект додавання$x$, відніміть$x$ з обох сторін рівняння.

\[\begin{aligned} x+a &= b \quad \color{Red} \text { Original equation. } \\ x+a-x &= b-x \quad \color{Red} \text { Subtract } x \text { from both sides. } \\ a &= b-x \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Зауважте, що ми маємо$a = \text {“Stuff”}$, де «Stu» не містить жодного входження змінної$a$, для якої ми вирішуємо.

Вправа$\PageIndex{2}$

Вирішити для$x : x-c=d$.

Відповідь: $c=x-d$

Приклад$\PageIndex{3}$

Формула$F = kx$, відома як «Закон Гука», передбачає силу,$F$ необхідну для розтягування$x$ пружинних одиниць. Розв'яжіть рівняння для$k$.

Рішення

Нам доручено вирішити рівняння$F = kx$ для$k$. Це означає, що наша кінцева відповідь повинна мати вигляд$k = \text {“Stuff”}$, де «Stu» є дійсним математичним виразом, який може містити інші змінні, математичні символи тощо, але він може не містити жодного входження змінної$k$. Це означає, що ми повинні ізолювати всі члени, що містять змінну з одного$k$ боку рівняння, а всі інші члени на іншій стороні рівняння. Однак зауважте, що всі члени, що містять$k$ змінну, вже ізольовані на одній стороні рівняння. Терміни, що не містять змінну$k$, виділяються з іншого боку рівняння. Тепер, щоб «скасувати» ефект множення на$x$, розділіть обидві сторони рівняння на$x$.

\[\begin{aligned} F&= kx \quad \color{Red} \text { Original equation. } \\ \dfrac{F}{x}&= \dfrac{kx}{x} \quad \color{Red} \text { Divide both sides by } x \\ \dfrac{F}{x}&= k \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Сказати, що$F/x = k$ це еквівалентно тому, що сказати$k = F/x$. Ми можемо залишити свою відповідь у формі, показаній на останньому кроці, але деякі інструктори наполягають на тому, щоб ми написали відповідь наступним чином:

\[k=\dfrac{F}{x} \quad \color{Red} \dfrac{F}{x}=k \text { is equivalent to } k=\dfrac{F}{x} \nonumber \]

Зауважте, що ми маємо$k = \text {“Stuff”}$, де «Stu» не містить жодного входження змінної$k$, для якої ми вирішуємо.

Вправа$\PageIndex{3}$

Вирішити для$m : E=m c^{2}$.

Відповідь: $m=\dfrac{E}{c^{2}}$

Приклад$\PageIndex{4}$

Формула$V = RI$ називається «Закон Ома». Він допомагає розрахувати падіння$V$ напруги на резисторі$R$ в електричному ланцюзі зі струмом$I$. Розв'яжіть рівняння для$R$.

Рішення

Нам доручено вирішити рівняння$V = RI$ для$R$. Це означає, що наша кінцева відповідь повинна мати вигляд$R = \text {“Stuff”}$, де «Stu» є дійсним математичним виразом, який може містити інші змінні, математичні символи тощо, але він може не містити жодного входження змінної$R$. Це означає, що ми повинні ізолювати всі члени, що містять змінну з одного$R$ боку рівняння, а всі інші члени на іншій стороні рівняння. Однак зауважте, що всі члени, що містять$R$ змінну, вже ізольовані на одній стороні рівняння. З іншого боку рівняння виділяють члени, що не містять змінну R. Тепер, щоб «скасувати» ефект множення на$I$, розділіть обидві сторони рівняння на$I$.

\[\begin{aligned} V&= R I \quad \color{Red} \text { Original equation. } \\ \dfrac{V}{I}&=\dfrac{R I}{I} \quad \color{Red} \text { Divide both sides by } I \\ \dfrac{V}{I}&= R \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Це також може бути написано в наступному вигляді:

\[R=\dfrac{V}{I} \quad \color{Red} V / I=R \text { is equivalent to } R=V / I \nonumber \]

Зауважте, що ми маємо$R = \text {“Stuff”}$, де «Stu» не містить жодного входження змінної$R$, для якої ми вирішуємо.

Вправа$\PageIndex{4}$

Вирішити для$t : d=s t$.

Відповідь: $t=\dfrac{d}{s}$

Очищення дробів

Якщо дроби зустрічаються у формулі, очистіть дроби з формули, множивши обидві сторони формули на загальний знаменник.

Приклад$\PageIndex{5}$

Формула$K=\dfrac{1}{2} m v^{2}$ використовується для розрахунку$K$ кінетичної енергії частинки маси, що$m$ рухається зі швидкістю$v$. Розв'яжіть рівняння для$m$.

Рішення

Нас просять вирішити рівняння$K = (1 /2)mv^2$ для$m$. Спочатку очистіть дроби, помноживши обидві сторони на загальний знаменник.

\[\begin{aligned} K &= \dfrac{1}{2} mv^{2} \quad \color{Red} \text { Original equation. } \\ 2(K) &= 2\left(\dfrac{1}{2} mv^{2}\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2K &= mv^{2} \quad \color{Red} \text { Simplify. Cancel } 2^{\prime} \text { s. } \end{aligned} \nonumber \]

Зверніть увагу, що всі члени$m$, що містять змінну, для якої ми розв'язуємо, вже ізольовані на одній стороні рівняння. Нам потрібно лише розділити обидві сторони на$v^2$, щоб завершити рішення.

\[\begin{aligned} \dfrac{2 K}{v^2}&= \dfrac{m v^{2}}{v^{2}} \quad \color{Red} \text { Divide both sides by } v^{2} \\ \dfrac{2 K}{v^2}&= m \quad \color{Red} \text { Simplify. Cancel } v^{2} \text { for } v^{2} \end{aligned} \nonumber \]

Зауважте, що кінцева відповідь має вигляд$m = \text {“Stuff”}$, де «Stu» не містить жодного входження змінної$m$.

Вправа$\PageIndex{5}$

Вирішити для$g : s=\dfrac{1}{2} g t^{2}$.

Відповідь: $g=\dfrac{2 s}{t^{2}}$

Приклад$\PageIndex{6}$

Як уже згадувалося раніше, Універсальний закон тяжіння Ньютона описується формулою\[F=\dfrac{G M m}{r^{2}} \nonumber \] Розв'яжіть це рівняння для$m$.

Рішення

Нас просять вирішити рівняння$F = GMm/r^2$ для$m$. Спочатку очистіть дроби, помноживши обидві сторони на загальний знаменник.

\[\begin{aligned} F &= \dfrac{G M m}{r^{2}} \quad \color{Red} \text { Original equation. } \\ r^{2}(F) &= r^{2}\left(\dfrac{G M m}{r^{2}}\right) \quad \color{Red} \text { Multiply both sides by } r^{2} \\ r^{2} F &= G M m \quad \color{Red} \text { Simplify. Cancel } r^{2} \text { for } r^{2} \end{aligned} \nonumber \]

Зверніть увагу, що всі члени$m$, що містять змінну, для якої ми розв'язуємо, вже ізольовані на одній стороні рівняння. Нам потрібно лише розділити обидві сторони на$GM$, щоб завершити рішення.

\[\begin{aligned} \dfrac{r^{2} F}{G M}&= \dfrac{G M m}{G M} \quad \color{Red} \text { Divide both sides by } G M \\ \dfrac{r^{2} F}{G M}&= m \quad \color{Red} \text { Simplify. Cancel } G M \text { for } G M \end{aligned} \nonumber \]

Зауважте, що кінцева відповідь має вигляд$m = \text {“Stuff”}$, де «Stu» не містить жодного входження змінної$m$.

Вправа$\PageIndex{6}$

Вирішити для$q_{2} : F=\dfrac{k q_{1} q_{2}}{r^{2}}$.

Відповідь: $q_{2}=\dfrac{F r^{2}}{k q_{1}}$

Геометричні формули

Давайте розглянемо кілька часто використовуваних формул з геометрії.

Приклад$\PageIndex{7}$

$W$$L$Дозволяти і представляють ширину і довжину прямокутника, відповідно, і нехай$P$ представляють його периметр.

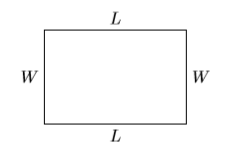
$рис. 2.4.1a.png$

Периметр (відстань навколо) прямокутника знаходять шляхом підсумовування його чотирьох сторін, а потім об'єднання подібних термінів.

\[\begin{aligned} P&=L+W+L+W \quad \color{Red} \text { Summing the four sides. } \\ P&=2 W+2L \quad \color{Red} \text { Combine like terms. } \end{aligned} \nonumber \]

Вирішити$P =2W +2L$ для$L$. Потім, з огляду на, що периметр -$300$ ноги, а ширина -$50$ фути, використовуйте свій результат для обчислення довжини.

Рішення

Нас спочатку просять вирішити$P =2W +2L$$L$. Спочатку виділіть всі члени, що містять змінну з одного$L$ боку рівняння.

\[\begin{aligned} P&= 2W+2L \quad \color{Red} \text { Original equation. } \\ P-2W&= 2W+2L-2W \quad \color{Red} \text { Subtract } 2W \text { from both sides. } \\ P-2W&= 2L \quad \color{Red} \text { Simplify. } \\ \dfrac{P-2W}{2}&= \dfrac{2L}{2} \quad \color{Red} \text { Divide both sides by } 2 \\ \dfrac{P-2W}{2}&=L \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Зауважте, що кінцевий результат має$L = \text {“Stuff"}$, де «Stu» не містить жодного входження змінної$L$.

Друга частина цього прикладу вимагає знайти довжину прямокутника, враховуючи, що периметр -$P = 300$ фути, а ширина -$W = 50$ фути. Щоб розрахувати довжину, підставляємо$P = 300$ і$W = 50$ в$L =( P - 2W)/2$.

\[\begin{aligned} &L= \dfrac{P-2 W}{2} \quad \color{Red} \text { Perimeter formula solved for } L \\ L&= \dfrac{300-2(50)}{2} \quad \color{Red} 300 \text { for } P, 50 \text { for } W\\ L &= \dfrac{300-100}{2} \quad \color{Red} \text { Multiply: } 2(50)=100 \\ L &= \dfrac{200}{2} \quad \color{Red} \text { Subtract: } 300-100=200 \\ L &= 100 \quad \color{Red} \text { Divide: } 200 / 2=100 \end{aligned} \nonumber \]

Отже, довжина прямокутника -$100$ фути.

Вправа$\PageIndex{7}$

Периметр прямокутника -$160$ метри, а його ширина -$30$ метри. Знаходить свою довжину.

Відповідь: $L=50$метрів

Приклад$\PageIndex{8}$

$b$$h$Дозволяти і представляють довжину підстави і висоту трикутника, відповідно, і нехай$A$ представляють площу трикутника.

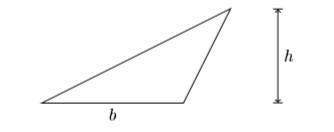
$рис. 2.4.1b.png$

Площа трикутника обчислюється за формулою:$A=\dfrac{1}{2} bh$ Тобто площа трикутника дорівнює «половині підстави на висоту».

Вирішити формулу$A=\dfrac{1}{2} bh$ для$h$. По-друге, враховуючи, що площа знаходиться$A = 90$ в ² ($90$квадратні дюйми), а довжина основи -$15$ в ($15$дюймах), знайдіть висоту трикутника.

Рішення

Нас спочатку просять вирішити$A = (1 /2)bh$$h$. Оскільки рівняння має дроби, першим кроком є очищення дробів шляхом множення обох сторін на найменш спільний знаменник.

\[\begin{aligned} A &= \dfrac{1}{2} bh \quad \color{Red} \text { Area of a triangle formula. } \\ 2(A) &= 2\left(\dfrac{1}{2} bh\right) \quad \color{Red} \text { Multiply both sides by } 2 \\ 2A &= bh \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Тепер у нас вже є всі члени, що містять змінну$h$ на одній стороні рівняння, тому ми можемо вирішити для,$h$ діливши обидві сторони рівняння на$b$.

\[\begin{aligned} \dfrac{2 A}{b}&= \dfrac{b h}{b} \quad \color{Red} \text { Divide both sides by } b \\ \dfrac{2 A}{b}&= h \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Зауважте, що кінцевий результат має$h = \text {“Stuff"}$, де «Stu» не містить жодного входження змінної$h$.

Друга частина цього прикладу вимагає, щоб ми знайшли висоту трикутника, враховуючи, що площа знаходиться$A = 90$ в$2$ і довжина основи знаходиться$b = 15$ в. Щоб обчислити висоту трикутника, підставляємо$A = 90$ і$b = 15$ в$h =2A/b$.

\[\begin{aligned} h &= \dfrac{2 A}{b} \quad \color{Red} \text { Area formula solved for } h \\ h &= \dfrac{2(90)}{15} \quad \color{Red} \text {Substitue }90 \text { for } A, 15 \text { for } b\\ h &=\dfrac{180}{15} \quad \color{Red} \text { Multiply: } 2(90)=180 \\ h &= 12 \quad \color{Red} \text {Divide: } 180 / 15=12 \end{aligned} \nonumber \]

Значить, висота трикутника дорівнює$12$ дюймам.

Вправа$\PageIndex{8}$

Площа трикутника -$140$ см ², а довжина його підстави -$70$ см. Знайдіть висоту трикутника.

Відповідь: $4$см