12.4: Обертання осей
- Page ID
- 59462
- Визначте невироджені конічні перерізи за умови їх загального вигляду рівнянь.
- Використовуйте формули обертання осей.
- Запишіть рівняння повернутих коніків в стандартному вигляді.
- Визначте коніки без обертових осей.
Як ми бачили, конічні перерізи утворюються, коли площина перетинає два правих кругових конуса, вирівняні кінчиком до кінчика і простягаються нескінченно далеко в протилежних напрямках, які ми також називаємо конусом. Спосіб, яким ми нарізаємо конус, визначить тип конічного перерізу, утвореного на перетині. Коло утворюється шляхом нарізки конуса площиною, перпендикулярною осі симетрії конуса. Еліпс утворюється шляхом нарізки єдиного конуса з похилою площиною, не перпендикулярною осі симетрії. Парабола утворюється шляхом нарізки площини через верх або низ подвійного конуса, тоді як гіпербола утворюється, коли площина зрізає як верхню, так і нижню частину конуса (рис.\(\PageIndex{1}\)).
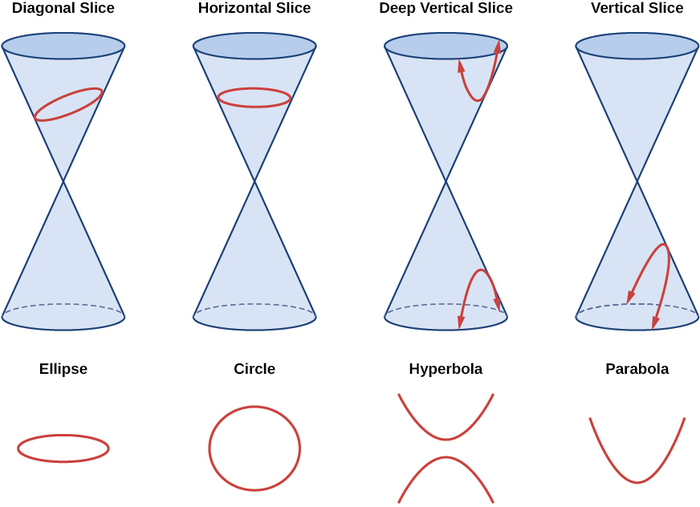
Рисунок\(\PageIndex{1}\): Невироджені конічні перерізи
Еліпси, кола, гіперболи та параболи іноді називають невиродженими конічними перерізами, на відміну від вироджених конічних перерізів, які показані на малюнку\(\PageIndex{2}\). Вироджений конічний результат, коли площина перетинає подвійний конус і проходить через верхівку. Залежно від кута площини можливі три типи вироджених конічних перерізів: точка, пряма або дві пересічні лінії.
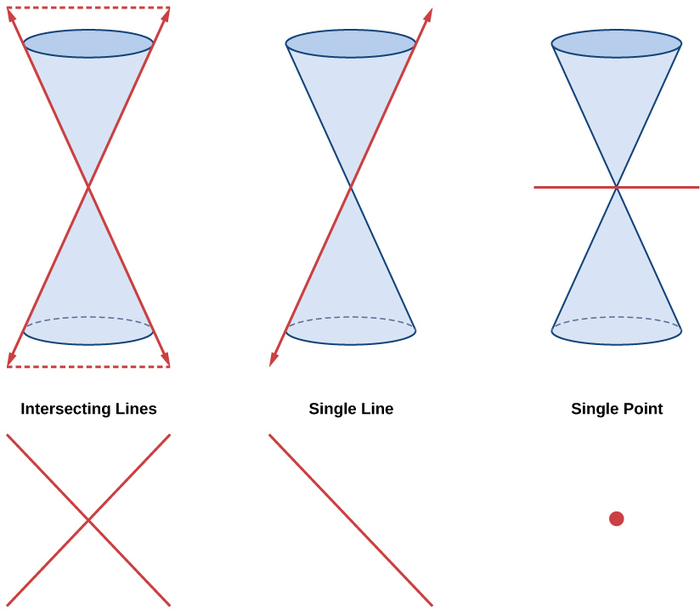
Малюнок\(\PageIndex{2}\): Вироджені конічні перерізи
Виявлення невироджених коніків у загальній формі
У попередніх розділах цієї глави ми зосередилися на рівняннях стандартної форми для невироджених конічних перерізів. У цьому розділі ми змістимо фокус на загальне рівняння форми, яке може бути використано для будь-якого конічного конуса. Загальна форма встановлюється рівною нулю, а терміни і коефіцієнти наведені в певному порядку, як показано нижче.
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
де\(A\)\(B\), і\(C\) не всі нуль. Ми можемо використовувати значення коефіцієнтів, щоб визначити, який тип коніки представлений заданим рівнянням.
Ви можете помітити, що загальне рівняння форми має\(xy\) термін, який ми не бачили ні в одному з рівнянь стандартної форми. Як ми будемо обговорювати пізніше,\(xy\) термін обертає конічне значення кожного разу\(B\), коли не дорівнює нулю.
| Конічні перерізи | Приклад |
|---|---|
| еліпс | \(4x^2+9y^2=1\) |
| коло | \(4x^2+4y^2=1\) |
| гіпербола | \(4x^2−9y^2=1\) |
| парабола | \(4x^2=9y\)або\(4y^2=9x\) |
| один рядок | \(4x+9y=1\) |
| перетинаються лінії | \((x−4)(y+4)=0\) |
| паралельні лінії | \((x−4)(x−9)=0\) |
| точка | \(4x^2+4y^2=0\) |
| немає графіка | \(4x^2+4y^2=−1\) |
Конічний перетин має загальний вигляд.
\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \label{gen}\]
де\(A\)\(B\), і\(C\) не всі нуль. Таблиця\(\PageIndex{2}\) підсумовує різні конічні перерізи де\(B=0\),\(A\) і\(C\) є ненульовими дійсними числами. Це вказує на те, що конічний конус не був повернутий.
| еліпс | \(Ax^2+Cy^2+Dx+Ey+F=0\),\(A≠C\) і\(AC>0\) |
|---|---|
| коло | \(Ax^2+Cy^2+Dx+Ey+F=0\),\(A=C\) |
| гіпербола | \(Ax^2−Cy^2+Dx+Ey+F=0\)або\(−Ax^2+Cy^2+Dx+Ey+F=0\), де\(A\) і\(C\) є позитивними |
| парабола | \(Ax^2+Dx+Ey+F=0\)або\(Cy^2+Dx+Ey+F=0\) |
- Перепишіть рівняння в загальному вигляді (Equation\ ref {gen}),\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
- Визначте значення\(A\) і\(C\) з загальної форми.
- Якщо\(A\) і\(C\) ненульові, мають однаковий знак і не рівні один одному, то граф може бути еліпсом.
- Якщо\(A\) і\(C\) рівні і ненульові і мають однаковий знак, то графік може бути колом.
- Якщо\(A\) і\(C\) є ненульовими і мають протилежні знаки, то графік може бути гіперболою.
- Якщо\(A\) або\(C\) дорівнює нулю, то графік може бути параболою.
Якщо\(B=0\), конічний переріз матиме вертикальні і/або горизонтальні осі. Якщо\(B\) не дорівнює 0, як показано нижче, конічний переріз повертається. Зверніть увагу на фразу «може бути» у визначеннях. Це тому, що рівняння може взагалі не представляти конічного перерізу, залежно від значень\(A\)\(B\),\(C\),\(D\),\(E\), і\(F\). Наприклад, виродженим випадком кола або еліпса є точка:
\[Ax^2+By^2=0,\]
коли\(A\) і\(B\) мають однаковий знак.
Вироджений випадок гіперболи - це дві пересічні прямі:\(Ax^2+By^2=0\), коли\(A\) і\(B\) мають протилежні ознаки.
З іншого боку, рівняння\(Ax^2+By^2+1=0\), коли\(A\) і\(B\) є додатними, взагалі не представляє графіка, оскільки немає реальних впорядкованих пар, які його задовольняють.
Визначте графік кожного з наступних невироджених конічних перерізів.
- \(4x^2−9y^2+36x+36y−125=0\)
- \(9y^2+16x+36y−10=0\)
- \(3x^2+3y^2−2x−6y−4=0\)
- \(−25x^2−4y^2+100x+16y+20=0\)
Рішення
- Переписуючи загальну форму (Equation\ ref {gen}), ми маємо\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 125 ) &= 0 \end{align*}\] з\(A=4\) і\(C=−9\), тому спостерігаємо, що\(A\) і\(C\) мають протилежні знаки. Графік цього рівняння - гіпербола.
- Переписуючи загальний вигляд (Equation\ ref {gen}), маємо\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 10 ) &= 0 \end{align*}\] з\(A=0\) і\(C=9\). Ми можемо визначити, що рівняння є параболою, оскільки\(A\) дорівнює нулю.
- Переписуючи загальний вигляд (Equation\ ref {gen}), маємо\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) &= 0 \end{align*}\] з\(A=3\) і\(C=3\). Тому що\(A=C\), графік цього рівняння - це коло.
- Переписуючи загальний вигляд (Equation\ ref {gen}), маємо\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] ( - 25 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 100 x + 16 y + 20 &= 0 \end{align*}\] з\(A=−25\) і\(C=−4\). Тому що\(AC>0\) і\(A≠C\), графік цього рівняння є еліпсом.
Визначте графік кожного з наступних невироджених конічних перерізів.
- \(16y^2−x^2+x−4y−9=0\)
- \(16x^2+4y^2+16x+49y−81=0\)
- Відповідь на
-
гіпербола
- Відповідь б
-
еліпс
Пошук нового подання заданого рівняння після обертання через заданий кут
До сих пір ми розглянули рівняння конічних перерізів без\(xy\) члена, який вирівнює графіки з осями x - і y. Коли ми додаємо\(xy\) термін, ми обертаємо конічний про походження. Якщо осі x - і y повернені на кут, скажімо\(\theta\), то кожна точка на площині може розглядатися як має два уявлення:\((x,y)\) на декартовій площині з початковою віссю x і y -віссю, і\((x^\prime ,y^\prime )\) на новій площині визначається новими, повернутими осями, які називаються осями x 'і y' -віссю (рис.\(\PageIndex{3}\)).
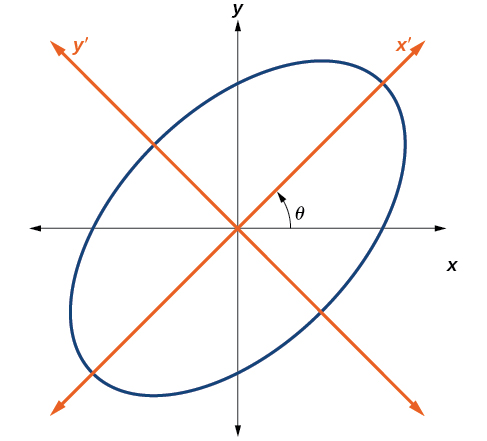
Малюнок\(\PageIndex{3}\): Графік оберненого еліпса\(x^2+y^2–xy–15=0\)
Ми знайдемо співвідношення між декартовою площиною\(x\) і\(y\) на\(y^\prime \) ній\(x^\prime \) і на новій повернутій площині (рис.\(\PageIndex{4}\)).
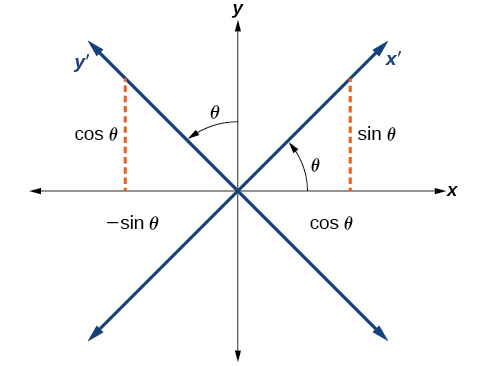
Малюнок\(\PageIndex{4}\): Декартова площина з\(y\) осями\(x\) - і -та результуючими осями\(x^\prime\) − та\(y^\prime\) −осями, утвореними поворотом на кут\(\theta\).
Початкові координати x - і y -осі мають одиничні вектори\(\hat{i}\) і\(\hat{j}\). Повернуті координатні\(\hat{i}^\prime\) осі мають одиничні вектори\(\hat{j}^\prime\) і.Кут\(\theta\) відомий як кут повороту (рис.\(\PageIndex{5}\)). Ми можемо записати нові одиничні вектори в терміні оригінальних.
\[\hat{i}′=\cos \theta \hat{i}+\sin \theta \hat{j}\]
\[\hat{j}′=−\sin \theta \hat{i}+\cos \theta \hat{j}\]
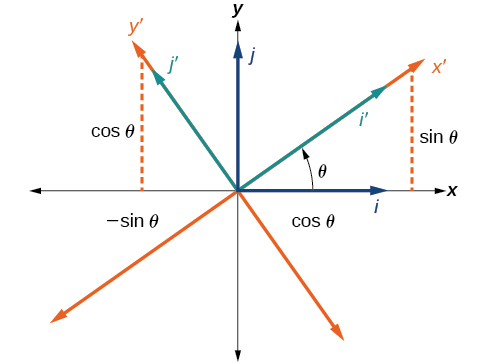
Малюнок\(\PageIndex{5}\): Відносини між старою і новою координатними площинами.
Розглянемо вектор\(\vec{u}\) в новій координатній площині. Він може бути представлений у вигляді його координатних осей.
\[\begin{align*} \vec{u}&=x^\prime i′+y^\prime j′ \\[4pt] &=x^\prime (i \cos \theta+j \sin \theta)+y^\prime (−i \sin \theta+j \cos \theta) & \text{Substitute.} \\[4pt] &=ix' \cos \theta+jx' \sin \theta−iy' \sin \theta+jy' \cos \theta & \text{Distribute.} \\[4pt] &=ix' \cos \theta−iy' \sin \theta+jx' \sin \theta+jy' \cos \theta & \text{Apply commutative property.} \\[4pt] &=(x' \cos \theta−y' \sin \theta)i+(x' \sin \theta+y' \cos \theta)j & \text{Factor by grouping.} \end{align*}\]
Тому що\(\vec{u}=x^\prime i′+y^\prime j′\), ми маємо уявлення\(x\) і з\(y\) точки зору нової системи координат.
\(x=x^\prime \cos \theta−y^\prime \sin \theta\)
і
\(y=x^\prime \sin \theta+y^\prime \cos \theta\)
Якщо точка\((x,y)\) на декартовій площині представлена на новій координатній площині, де осі обертання утворюються обертанням кута\(\theta\) від позитивної осі х, то координати точки щодо нових осей є\((x^\prime ,y^\prime )\). Ми можемо використовувати наступні рівняння обертання для визначення співвідношення між\((x,y)\) і\((x^\prime , y^\prime )\):
\[x=x^\prime \cos \theta−y^\prime \sin \theta\]
і
\[y=x^\prime \sin \theta+y^\prime \cos \theta\]
- Знайти\(x\) і\(y\) де\(x=x^\prime \cos \theta−y^\prime \sin \theta\) і\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
- Підставте вираз для\(x\) і\(y\) в задане рівняння, а потім спростіть.
- Напишіть рівняння з\(x^\prime \) і\(y^\prime \) в стандартній формі.
Знайти нове уявлення рівняння\(2x^2−xy+2y^2−30=0\) після обертання на кут\(\theta=45°\).
Рішення
Знайти\(x\) і\(y\), де\(x=x^\prime \cos \theta−y^\prime \sin \theta\) і\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
Тому що\(\theta=45°\),
\[\begin{align*} x &= x^\prime \cos(45°)−y^\prime \sin(45°) \\[4pt] x &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right)−y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] x &=\dfrac{x^\prime −y^\prime }{\sqrt{2}} \end{align*}\]
і
\[\begin{align*} y &= x^\prime \sin(45°)+y^\prime \cos(45°) \\[4pt] y &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right) + y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] y &= \dfrac{x^\prime +y^\prime }{\sqrt{2}} \end{align*}\]
\(y=x^\prime \sin \theta+y^\prime \cos \theta\)Підставляємо\(x=x^\prime \cos\theta−y^\prime \sin\theta\) і в\(2x^2−xy+2y^2−30=0\).
\(2{\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)}^2−\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)+2{\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)}^2−30=0\)
Спростити.
\(\begin{array}{rl} 2\dfrac{(x^\prime−y^\prime )(x^\prime −y^\prime )}{2}−\dfrac{(x^\prime −y^\prime )(x^\prime +y^\prime )}{2}+2\dfrac{(x^\prime +y^\prime )(x^\prime +y^\prime )}{2}−30=0 & \text{FOIL method} \\[4pt] {x^\prime }^2−2x^\prime y^\prime +{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}+{x^\prime }^2+2x^\prime y^\prime +{y^\prime }^2−30=0 & \text{Combine like terms.} \\[4pt] 2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}=30 & \text{Combine like terms.} \\[4pt] 2(2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2})=2(30) & \text{Multiply both sides by 2.} \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−({x^\prime }^2−{y^\prime }^2)=60 & \text{Simplify. } \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−{x^\prime }^2+{y^\prime }2=60 & \text{Distribute.} \\[4pt] \dfrac{3{x^\prime }^2}{60}+\dfrac{5{y^\prime }^2}{60}=\dfrac{60}{60} & \text{Set equal to 1.} \end{array} \)
Запишіть рівняння з\(x^\prime \) і\(y^\prime \) в стандартній формі.
\[\dfrac{{x^\prime }^2}{20}+\dfrac{{y^\prime}^2}{12}=1 \nonumber\]
Це рівняння є еліпсом. На\(\PageIndex{6}\) малюнку зображений графік.
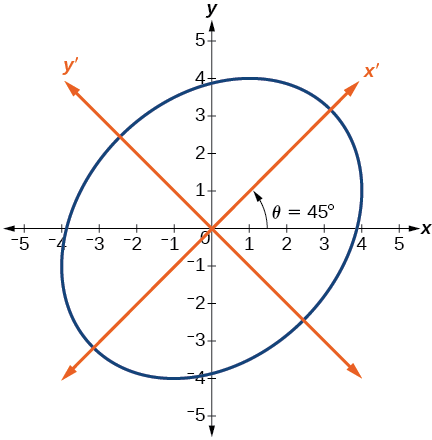
Малюнок\(\PageIndex{6}\)
Написання рівнянь обертових коніків у стандартній формі
Тепер, коли ми можемо знайти стандартну форму конічного конуса, коли нам задають кут повороту, ми навчимося перетворити рівняння конічного конуса, задане у вигляді,\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) в стандартну форму шляхом обертання осей. Для цього ми перепишемо загальну форму як рівняння в системі\(y^\prime \) координат\(x^\prime \) і без\(x^\prime y^\prime \) члена, обертаючи осі на міру,\(\theta\) яка задовольняє
\[\cot(2\theta)=\dfrac{A−C}{B}\]
Ми вже дізналися, що будь-який конічний конус може бути представлений рівнянням другого ступеня.
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
де\(A\)\(B\), і\(C\) не всі нуль. Однак якщо\(B≠0\), то у нас є\(xy\) термін, який заважає нам переписати рівняння в стандартній формі. Щоб усунути його, ми можемо повернути осі на гострий кут\(\theta\) де\(\cot(2\theta)=\dfrac{A−C}{B}\).
- Якщо\(\cot(2\theta)>0\), то\(2\theta\) знаходиться в першому квадранті, і\(\theta\) знаходиться між\((0°,45°)\).
- Якщо\(\cot(2\theta)<0\), то\(2\theta\) знаходиться в другому квадранті, і\(\theta\) знаходиться між\((45°,90°)\).
- Якщо\(A=C\), то\(\theta=45°\).
- Знайти\(\cot(2\theta)\).
- Знайти\(\sin \theta\) і\(\cos \theta\).
- \(\cos \theta\)Підставляємо\(\sin \theta\) і в\(x=x^\prime \cos \theta−y^\prime \sin \theta\) і\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
- Підставляємо вираз for\(x\) і\(y\) into в задане рівняння, а потім спрощуємо.
- Напишіть рівняння з\(x^\prime \) і\(y^\prime \) в стандартному вигляді щодо повернених осей.
Перепишіть рівняння\(8x^2−12xy+17y^2=20\) в\(x^\prime y^\prime \) системі без\(x^\prime y^\prime \) члена.
Рішення
Спочатку знаходимо\(\cot(2\theta)\).
\(8x^2−12xy+17y^2=20\rightarrow A=8\),\(B=−12\) і\(C=17\)
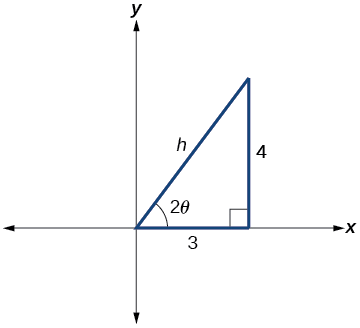
Малюнок\(\PageIndex{7}\)
З малюнка\(\PageIndex{7}\):
\[ \begin{align*} \cot(2\theta) &=\dfrac{A−C}{B}=\dfrac{8−17}{−12} \\[4pt] & =\dfrac{−9}{−12}=\dfrac{3}{4} \end{align*}\]
\(\cot(2\theta)=\dfrac{3}{4}=\dfrac{\text{adjacent}}{\text{opposite}}\)
Отже, гіпотенуза
\[ \begin{align*} 3^2+4^2 &=h^2 \\[4pt] 9+16 &=h^2 \\[4pt] 25&=h^2 \\[4pt] h&=5 \end{align*}\]
Далі знаходимо\(\sin \theta\) і\(\cos \theta\).
\[ \begin{align*} \sin \theta &=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5−3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{2}{10}}=\sqrt{\dfrac{1}{5}} \\ \sin \theta &= \dfrac{1}{\sqrt{5}} \\ \cos \theta &= \sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5+3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{8}{10}}=\sqrt{\dfrac{4}{5}} \\ \cos \theta &= \dfrac{2}{\sqrt{5}} \end{align*}\]
Підставляємо значення\(\sin \theta\) і\(\cos \theta\) в\(x=x^\prime \cos \theta−y^\prime \sin \theta\) і\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
\[ \begin{align*} x &=x'\cos \theta−y^\prime \sin \theta \\[4pt] &=x^\prime \left(\dfrac{2}{\sqrt{5}}\right)−y^\prime \left(\dfrac{1}{\sqrt{5}}\right) \\[4pt] &=\dfrac{2x^\prime −y^\prime }{\sqrt{5}} \end{align*}\]
і
\[ \begin{align*} y&=x^\prime \sin \theta+y^\prime \cos \theta \\[4pt] &=x^\prime \left(\dfrac{1}{\sqrt{5}}\right)+y^\prime \left(\dfrac{2}{\sqrt{5}}\right) \\[4pt] &=\dfrac{x^\prime +2y^\prime }{\sqrt{5}} \end{align*}\]
Підставте вирази для\(x\) і\(y\) в задане рівняння, а потім спростіть.
\[ \begin{align*} 8{\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)}^2−12\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)+17{\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)}^2&=20 \\[4pt] 8\left(\dfrac{(2x^\prime −y^\prime )(2x^\prime −y^\prime )}{5}\right)−12\left(\dfrac{(2x^\prime −y^\prime )(x^\prime +2y^\prime )}{5}\right)+17\left(\dfrac{(x^\prime +2y^\prime )(x^\prime +2y^\prime )}{5}\right)&=20 \\[4pt] 8(4{x^\prime }^2−4x^\prime y^\prime +{y^\prime }^2)−12(2{x^\prime }^2+3x^\prime y^\prime −2{y^\prime }^2)+17({x^\prime }^2+4x^\prime y^\prime +4{y^\prime }^2)&=100 \\[4pt] 32{x^\prime }^2−32x^\prime y^\prime +8{y^\prime }^2−24{x^\prime }^2−36x^\prime y^\prime +24{y^\prime }^2+17{x^\prime }^2+68x^\prime y^\prime +68{y^\prime }^2&=100 \\[4pt] 25{x^\prime }^2+100{y^\prime }^2&=100 \\[4pt] \dfrac{25}{100}{x^\prime }^2+\dfrac{100}{100}{y^\prime }^2&=\dfrac{100}{100} \end{align*}\]
Запишіть рівняння з\(x^\prime \) і\(y^\prime \) в стандартному вигляді щодо нової системи координат.
\[\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1 \nonumber\]
\(\PageIndex{8}\)На малюнку зображений графік еліпса.
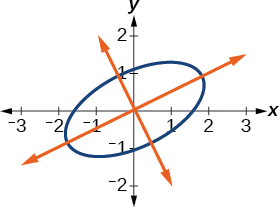
Малюнок\(\PageIndex{8}\)
Перепишіть\(13x^2−6\sqrt{3}xy+7y^2=16\) в\(x^\prime y^\prime \) систему без\(x^\prime y^\prime \) терміну.
- Відповідь
-
\(\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1\)
Графік наведено наступне рівняння щодо\(x^\prime y^\prime \) системи:
\(x^2+12xy−4y^2=30\)
Рішення
Спочатку знаходимо\(\cot(2\theta)\).
\(x^2+12xy−4y^2=20\rightarrow A=1\),\(B=12\), і\(C=−4\)
\[\begin{align*} \cot(2\theta) &= \dfrac{A−C}{B} \\ \cot(2\theta) &= \dfrac{1−(−4)}{12} \\ \cot(2\theta) &= \dfrac{5}{12} \end{align*}\]
Тому що\(\cot(2\theta)=\dfrac{5}{12}\), ми можемо намалювати опорний трикутник, як на малюнку\(\PageIndex{9}\).
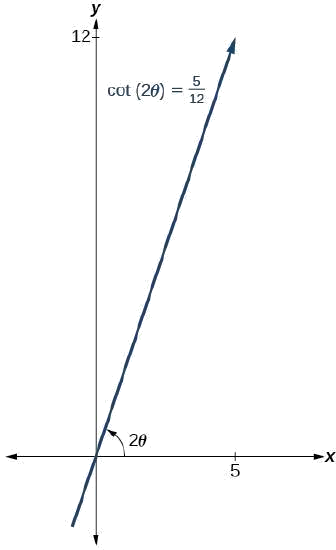
Малюнок\(\PageIndex{9}\)
\(\cot(2\theta)=\dfrac{5}{12}=\dfrac{adjacent}{opposite}\)
Таким чином, гіпотенуза становить
\[ \begin{align*} 5^2+{12}^2&=h^2 \\[4pt] 25+144 &=h^2 \\[4pt] 169 &=h^2 \\[4pt] h&=13 \end{align*}\]
Далі знаходимо\(\sin \theta\) і\(\cos \theta\). Ми будемо використовувати напівкутові тотожності.
\(\sin \theta=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{8}{13}⋅\dfrac{1}{2}}=\dfrac{2}{\sqrt{13}}\)
\(\cos \theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{18}{13}⋅\dfrac{1}{2}}=\dfrac{3}{\sqrt{13}}\)
Тепер знаходимо\(x\) і\(y\).
\(x=x^\prime \cos \theta−y^\prime \sin \theta\)
\(x=x^\prime \left(\dfrac{3}{\sqrt{13}}\right)−y^\prime \left(\dfrac{2}{\sqrt{13}}\right)\)
\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\)
і
\(y=x^\prime \sin \theta+y^\prime \cos \theta\)
\(y=x^\prime \left(\dfrac{2}{\sqrt{13}}\right)+y^\prime \left(\dfrac{3}{\sqrt{13}}\right)\)
\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\)
Тепер підставляємо\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\) і\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\) в\(x^2+12xy−4y^2=30\).
\(\begin{array}{rl} {\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)}^2+12\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)−4{\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)}^2=30 \\ \left(\dfrac{1}{13}\right)[ {(3x^\prime −2y^\prime )}^2+12(3x^\prime −2y^\prime )(2x^\prime +3y^\prime )−4{(2x^\prime +3y^\prime )}^2 ]=30 & \text{Factor.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+12(6{x^\prime }^2+5x^\prime y^\prime −6{y^\prime }^2)−4(4{x^\prime }^2+12x^\prime y^\prime +9{y^\prime }^2) ]=30 & \text{Multiply.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+72{x^\prime }^2+60x^\prime y^\prime −72{y^\prime }^2−16{x^\prime }^2−48x^\prime y^\prime −36{y^\prime }^2 ]=30 & \text{Distribute.} \\ \left(\dfrac{1}{13}\right)[ 65{x^\prime }^2−104{y^\prime }^2 ]=30 & \text{Combine like terms.} \\ 65{x^\prime }^2−104{y^\prime }^2=390 & \text{Multiply.} \\ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 & \text{Divide by 390.} \end{array}\)
\(\PageIndex{10}\)На малюнку показаний графік гіперболи\(\dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1\)
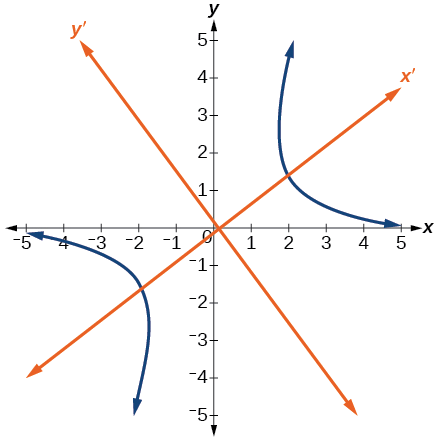
Малюнок\(\PageIndex{10}\)
Визначення коніків без обертових осей
Тепер ми підійшли до повного кола. Як ми ідентифікуємо тип конічного конуса, описаний рівнянням? Що відбувається при обертанні осей? Нагадаємо, загальна форма конічного перерізу дорівнює
\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
Якщо застосувати до цього рівняння формули обертання, то отримаємо вигляд.
\(A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\)
Може бути показано, що
\(B^2−4AC={B′}^2−4A′C′\)
Вираз не змінюється після обертання, тому ми називаємо вираз інваріантним. Дискримінантний\(B^2−4AC\), є інваріантним і залишається незмінним після обертання. Оскільки дискримінант залишається незмінним, спостереження за дискримінантом дозволяє ідентифікувати конічний переріз.
Якщо рівняння
\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]
перетворюється обертовими осями в рівняння
\[A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\]
потім\[B^2−4AC={B′}^2−4A′C′\]
Рівняння\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) є еліпсом, параболою або гіперболою, або виродженим випадком одного з них. Якщо дискримінант,\(B^2−4AC\), є
- \(<0\), конічний переріз - еліпс
- \(=0\), конічний перетин - парабола
- \(>0\), конічний розріз - гіпербола
Визначте конус для кожного з наступних без обертових осей.
- \(5x^2+2\sqrt{3}xy+2y^2−5=0\)
- \(5x^2+2\sqrt{3}xy+12y^2−5=0\)
Рішення
а Почнемо з визначення\(A\)\(B\), і\(C\).
\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{2}_{C}y^2−5=0\)
Тепер ми знаходимо дискримінант.
\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(2) \\ &=4(3)−40 \\ &=12−40 \\ &=−28<0 \end{align*}\]
Тому\(5x^2+2\sqrt{3}xy+2y^2−5=0\) являє собою еліпс.
б. знову почнемо з визначення\(A\)\(B\), і\(C\).
\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{12}_{C}y^2−5=0 \nonumber\)
Тепер ми знаходимо дискримінант.
\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(12) \\ &= 4(3)−240 \\ &= 12−240 \\ &=−228<0 \end{align*}\]
Тому\(5x^2+2\sqrt{3}xy+12y^2−5=0\) являє собою еліпс.
Визначте конус для кожного з наступних без обертових осей.
- \(x^2−9xy+3y^2−12=0\)
- \(10x^2−9xy+4y^2−4=0\)
- Відповідь на
-
гіпербола
- Відповідь б
-
еліпс
Ключові рівняння
| Загальне рівняння форми конічного перерізу | \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) |
| Обертання конічного перерізу |
\(x=x^\prime \cos \theta−y^\prime \sin \theta\) \(y=x^\prime \sin \theta+y^\prime \cos \theta\) |
| Кут повороту | \(\theta\), де\(\cot(2\theta)=\dfrac{A−C}{B}\) |
Ключові концепції
- Чотири основні форми можуть бути результатом перетину площини з парою правих кругових конусів, з'єднаних хвіст з хвостом. Вони включають еліпс, коло, гіперболу та параболу.
- Невироджений конічний переріз має загальний вигляд\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) де\(A\),\(B\) і\(C\) не всі нулі. Значення\(A\)\(B\), і\(C\) визначають тип конічного конуса. Див\(\PageIndex{1}\). Приклад.
- Рівняння конічних перерізів з\(xy\) терміном обертали навколо початку. Див\(\PageIndex{2}\). Приклад.
- Загальна форма може бути перетворена в рівняння в системі\(y^\prime \) координат\(x^\prime \) і без\(x^\prime y^\prime \) члена. Див. приклад\(\PageIndex{3}\) і приклад\(\PageIndex{4}\).
- Вираз описується як інваріантний, якщо він залишається незмінним після обертання. Оскільки дискримінант є інваріантним, спостереження за ним дозволяє ідентифікувати конічний переріз. Див\(\PageIndex{5}\). Приклад.
