11.8: Розв'язування систем за допомогою правила Крамера
- Page ID
- 59212
- Оцініть 2 × 2 детермінанти.
- Використовуйте Правило Крамера для вирішення системи рівнянь у двох змінних.
- Оцініть 3 × 3 детермінанти.
- Використовуйте Правило Крамера для вирішення системи з трьох рівнянь у трьох змінних.
- Знати властивості детермінант.
Ми навчилися розв'язувати системи рівнянь у двох змінних та трьох змінних, а також декількома методами: заміщення, додавання, гаусове усунення, використання зворотної матриці та графікування. Деякі з цих методів легше застосовувати, ніж інші і більш доречні в певних ситуаціях. У цьому розділі ми вивчимо ще дві стратегії розв'язання систем рівнянь.
Оцінка детермінанти матриці 2 × 2
Детермінант - це дійсне число, яке може бути дуже корисним у математиці, оскільки воно має кілька застосувань, таких як обчислення площі, обсягу та інших величин. Тут ми будемо використовувати детермінанти, щоб виявити, чи є матриця оборотною, використовуючи записи квадратної матриці, щоб визначити, чи є рішення системи рівнянь. Мабуть, одним з найбільш цікавих додатків, однак, є їх використання в криптографії. Безпечні сигнали або повідомлення іноді надсилаються закодованими в матриці. Дані можна розшифрувати лише за допомогою оборотної матриці та визначника. Для наших цілей ми орієнтуємося на детермінант як вказівку на оборотність матриці. Обчислення детермінанта матриці передбачає дотримання конкретних закономірностей, які викладені в цьому розділі.
Визначник матриці 2 × 2, заданий
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
визначається як

Зверніть увагу на зміну позначень. Існує кілька способів позначення визначника, в тому числі\(\det(A)\) і заміна дужок в матриці з прямими лініями,\(| A |\).
Знайти детермінант заданої матриці.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Рішення
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]
Використання правила Крамера для розв'язання системи двох рівнянь у двох змінних
Тепер ми введемо остаточний метод розв'язання систем рівнянь, який використовує детермінанти. Відомий як правило Крамера, ця методика датується серединою 18 століття і названа на честь свого новатора, швейцарського математика Габріеля Крамера (1704-1752), який представив її в 1750 р. Введення à l'Analyse des lignes Courbes algébriques. Правило Крамера є життєздатним і ефективним методом пошуку розв'язків систем з довільною кількістю невідомих, за умови, що ми маємо таку ж кількість рівнянь, як і невідомі.
Правило Крамера дасть нам унікальне рішення системи рівнянь, якщо воно існує. Однак якщо в системі немає рішення або нескінченного числа рішень, на це вкаже визначник нуль. Щоб з'ясувати, чи є система непослідовною або залежною, доведеться скористатися іншим методом, таким як усунення.
Щоб зрозуміти Правило Крамера, давайте уважно розглянемо, як ми вирішуємо системи лінійних рівнянь за допомогою основних рядкових операцій. Розглянемо систему з двох рівнянь у двох змінних.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Ми усуваємо одну змінну за допомогою рядкових операцій і вирішуємо для іншої. Скажіть, що ми хочемо вирішити за\(x\). Якщо рівняння\ ref {eq2} помножити на протилежний коефіцієнту\(y\) в Equation\ ref {eq1}, Equation\ ref {eq1} помножити на коефіцієнт\(y\) в Equation\ ref {eq2}, і ми додамо два рівняння, змінна\(y\) буде усунена.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Multiply }R_1 \text{ by }b_2 \\ -&\underline{b_1a_2x−b_1b_2y=−b_1c_2} & \text{Multiply }R_2 \text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]
Тепер вирішуйте для\(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Аналогічно вирішувати за\(y\), будемо ліквідувати\(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x−a_1b_2y=−a_1c_2} & \text{Multiply }R_2 \text{ by }−a_1 \\ & a_2b_1y−a_1b_2y =a_2c_1−a_1c_2 \end{align*}\]
Рішення для\(y\) дарує
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Зверніть увагу, що знаменник для обох\(x\) і\(y\) є визначником матриці коефіцієнтів.
Ми можемо використовувати ці формули для вирішення\(x\) і\(y\), але Правило Крамера також вводить нові позначення:
- \(D\):визначник матриці коефіцієнтів
- \(D_x\):визначник чисельника у розв'язку\(x\)
\[x=\dfrac{D_x}{D}\]
- \(D_y\):визначник чисельника у розв'язку\(y\)
\[y=\dfrac{D_y}{D}\]
Ключем до Правила Крамера є заміна змінного стовпця інтересу на постійний стовпець і обчислення визначників. Потім ми можемо висловити\(x\) і\(y\) як частку двох детермінант.
Правило Крамера - це метод, який використовує детермінанти для вирішення систем рівнянь, які мають таку ж кількість рівнянь, що і змінні.
Розглянемо систему з двох лінійних рівнянь у двох змінних.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
Рішення, що використовує правило Крамера, наведено як
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0 \end{align}\]
Якщо ми вирішуємо для\(x\),\(x\) стовпець замінюється постійним стовпцем. Якщо ми вирішуємо для\(y\),\(y\) стовпець замінюється постійним стовпцем.
Вирішіть\(2 × 2\) наступну систему за допомогою правила Крамера.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Рішення
Вирішити для\(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]
Вирішити для\(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align*}\]
Рішення є\((2,−3)\).
Використовуйте Правило Крамера для вирішення\(2 × 2\) системи рівнянь.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Відповідь
-
\((3,−7)\)
Оцінка детермінанти матриці 3 × 3
Знайти детермінант матриці 2×2 просто, але знайти детермінант матриці 3×3 складніше. Один з методів полягає в доповненні матриці 3 × 3 з повторенням перших двох стовпців, даючи матрицю 3×5. Потім обчислюємо суму добутків записів вниз по кожній з трьох діагоналей (зліва зверху вниз праворуч), і віднімаємо добуток записів вгору по кожній з трьох діагоналей (знизу зліва вгорі праворуч). Це легше зрозуміти на візуальному і прикладі.
Знайдіть детермінант матриці 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- \(A\)Доповнюємо першими двома стовпчиками.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- Зверху ліворуч до нижнього правого: множте записи вниз по першій діагоналі. Додайте результат до добутку записів вниз по другій діагоналі. Додайте цей результат до добутку записів вниз по третій діагоналі.
- Від нижнього лівого до верхнього праворуч: Відніміть добуток записів вгору по першій діагоналі. З цього результату віднімаємо добуток записів вгору по другій діагоналі. З цього результату відніміть добуток записів вгору по третій діагоналі.
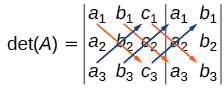
Алгебра виглядає наступним чином:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Знайти детермінант заданої\(3 × 3\) матриці
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Рішення
Доповніть матрицю першими двома стовпцями, а потім дотримуйтесь формули. Таким чином,
\[\begin{align*} | A | &= \left| \begin{array}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{array}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Знайдіть детермінант матриці 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Відповідь
-
\(−10\)
Ні, цей метод працює тільки для 2 × 2 і 3 × 3 матриць. Для великих матриць найкраще використовувати графічну утиліту або комп'ютерне програмне забезпечення.
Використання правила Крамера для розв'язання системи трьох рівнянь у трьох змінних
Тепер, коли ми можемо знайти детермінант\(3 × 3\) матриці, ми можемо застосувати Правило Крамера для вирішення системи з трьох рівнянь у трьох змінних. Правило Крамера є простим, дотримуючись шаблону, що відповідає Правилу Крамера для\(2 × 2\) матриць. При збільшенні порядку матриці до\(3 × 3\), однак, є набагато більше обчислень, необхідних.
Коли ми обчислюємо визначник нулем, Правило Крамера не дає жодних вказівок щодо того, чи не має система рішення або нескінченна кількість рішень. Щоб це з'ясувати, нам доведеться виконати ліквідацію в системі.
Розглянемо\(3 × 3\) систему рівнянь.
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue}d_3 \\ \end{align}\]
\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\),\(D≠0\)
де
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Якщо ми пишемо детермінант\(D_x\), то замінюємо\(x\) стовпець постійним стовпцем. Якщо ми пишемо детермінант\(D_y\), ми замінюємо їх y стовпець постійним стовпцем. Якщо ми пишемо детермінант\(D_z\), то замінюємо\(z\) стовпець постійним стовпцем. Завжди перевіряйте відповідь.
Знайдіть рішення даної\(3 × 3\) системи за допомогою правила Крамера.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Рішення
Використовуйте правило Крамера.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\),\(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\\14&3&−2\end{vmatrix}\),\(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\),\(D_z=\begin{vmatrix}1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Потім,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
Рішення є\((1,3,−2)\).
Використовуйте Правило Крамера для вирішення\(3 × 3\) матриці.
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Відповідь
-
\(\left(−2,\dfrac{3}{5},\dfrac{12}{5}\right)\)
Розв'яжіть систему рівнянь за допомогою Правила Крамера.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Рішення
Починаємо з пошуку детермінант\(D\)\(D_x\), і\(D_y\).
\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)
Ми знаємо, що детермінант нуля означає, що або система не має рішення, або вона має нескінченну кількість рішень. Щоб подивитися, який саме, використовуємо процес усунення. Наша мета - усунути одну зі змінних.
- Помножте рівняння\ ref {eq3} на\(−2\).
- Додайте результат до Рівняння\ ref {eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\;\;\;\;\; 0=−8 \end{align*}\]
Отримуємо рівняння\(0=−8\), яке є хибним. Тому система не має рішення. Графік системи виявляє дві паралельні лінії. Див\(\PageIndex{1}\). Малюнок.
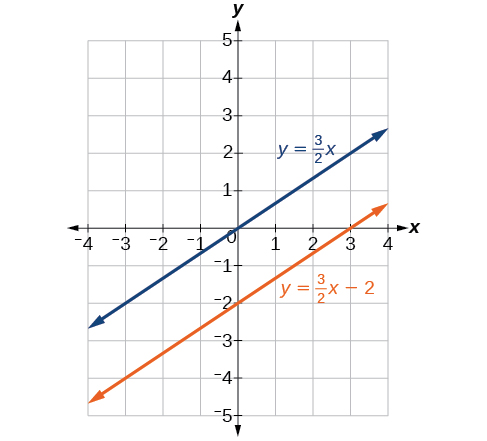
Вирішіть систему з нескінченною кількістю рішень.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end{align}\]
Рішення
Давайте спочатку знайдемо детермінант. Налаштуйте матрицю, доповнену першими двома стовпцями.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)
Потім,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0\)
Оскільки детермінант дорівнює нулю, існує або рішення, або нескінченна кількість розв'язків. Ми повинні виконати ліквідацію, щоб з'ясувати.
1. Помножте рівняння\ ref {eq5} на\(−2\) і додайте результат до Рівняння\ ref {eq7}:
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. Отримання відповіді\(0=0\), твердження, яке завжди вірно, означає, що система має нескінченну кількість рішень. Графікуючи систему, ми бачимо, що дві площини однакові, і вони обидві перетинають третю площину на лінії. Див\(\PageIndex{2}\). Малюнок.
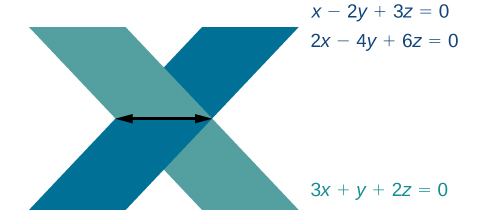
Розуміння властивостей детермінант
Існує безліч властивостей детермінант. Нижче наведено деякі властивості, які можуть бути корисними для обчислення визначника матриці.
- Якщо матриця має верхню трикутну форму, визначник дорівнює добутку записів вниз по головній діагоналі.
- Коли два ряди змінюються місцями, визначник змінює знак.
- Якщо два рядки або два стовпці ідентичні, визначник дорівнює нулю.
- Якщо матриця містить або рядок нулів, або стовпець нулів, визначник дорівнює нулю.
- Визначником оберненої матриці\(A^{−1}\) є зворотний детермінанту матриці\(A\).
- Якщо будь-який рядок або стовпець множиться на константу, визначник множиться на той же коефіцієнт.
Проілюструйте кожне з властивостей детермінант.
Рішення
Властивість 1 стверджує, що якщо матриця знаходиться у верхній трикутній формі, визначник є добутком записів вниз по головній діагоналі.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
\(A\)Доповнюємо першими двома стовпчиками.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)
Тоді
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
Властивість 2 стверджує, що перемикання рядків змінює знак. Враховується
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)(5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]
Властивість 3 стверджує, що якщо два рядки або два стовпці ідентичні, визначник дорівнює нулю.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{array}\right]\\ \det(A)&=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\\ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
Властивість 4 стверджує, що якщо рядок або стовпець дорівнює нулю, визначник дорівнює нулю. Таким чином,
\[\begin{align*} A&=\begin{bmatrix}1&2\\0&0\end{bmatrix}\\ \det(A)&=1(0)-2(0)\\ &=0 \end{align*}\]
Властивість 5 стверджує, що детермінант зворотної матриці\(A^{−1}\) є зворотним детермінанту\(A\). Таким чином,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-3(2)\\ &=-2 \end{align*}\]
\[\begin{align*} A^{-1}&=\begin{bmatrix}-2&1\\\dfrac{3}{2}&-\dfrac{1}{2}\end{bmatrix}\\ \det(A^{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \end{align*}\]
Властивість 6 стверджує, що якщо будь-який рядок або стовпець матриці множиться на константу, визначник множиться на той же коефіцієнт. Таким чином,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \end{align*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4)\\ &=-4 \end{align*}\]
Знайдіть рішення для даної\(3 × 3\) системи.
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\end{align}\]
Рішення
Використовуючи правило Крамера, ми маємо
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Зверніть увагу, що другий і третій стовпці ідентичні. Відповідно до Властивості 3, визначник буде дорівнює нулю, тому рішення або немає, або нескінченне число рішень. Ми повинні виконати ліквідацію, щоб з'ясувати.
1. Помножте рівняння\ ref {eq10} на\(–2\) і додайте результат до Рівняння\ ref {eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Отримання твердження, яке є протиріччям, означає, що система не має рішення.
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики за допомогою правила Крамера.
Ключові поняття
- Визначник для\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) є\(ad−bc\). Див\(\PageIndex{1}\). Приклад.
- Правило Крамера замінює змінний стовпець постійним стовпцем. Рішення є\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\). Див\(\PageIndex{2}\). Приклад.
- Щоб знайти детермінант\(3×3\) матриці, доповніть першими двома стовпцями. Додайте три діагональні записи (ліворуч зверху вниз праворуч) і відніміть три діагональні записи (знизу зліва вгорі праворуч). Див\(\PageIndex{3}\). Приклад.
- Щоб вирішити систему з трьох рівнянь у трьох змінних за допомогою Правила Крамера, замініть змінну колонку на постійну колонку для кожного потрібного рішення:\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\). Див\(\PageIndex{4}\). Приклад.
- Правило Крамера також корисно для пошуку розв'язку системи рівнянь без розв'язків або нескінченних розв'язків. Див. Приклад\(\PageIndex{5}\) і Приклад\(\PageIndex{6}\).
- Певні властивості детермінант корисні для вирішення завдань. Наприклад:
- Якщо матриця має верхню трикутну форму, визначник дорівнює добутку записів вниз по головній діагоналі.
- Коли два ряди змінюються місцями, визначник змінює знак.
- Якщо два рядки або два стовпці ідентичні, визначник дорівнює нулю.
- Якщо матриця містить або рядок нулів, або стовпець нулів, визначник дорівнює нулю.
- Визначником оберненої матриці\(A^{−1}\) є зворотний детермінанту матриці\(A\).
- Якщо будь-який рядок або стовпець множиться на константу, визначник множиться на той же коефіцієнт. Див. Приклад\(\PageIndex{7}\) і Приклад\(\PageIndex{8}\).
