Skip to main content
LibreTexts - Ukrayinska

11.2: Системи лінійних рівнянь з трьома змінними

  1. Last updated
  2. Save as PDF
  • Page ID
    59225

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Розв'яжіть системи трьох рівнянь у трьох змінних.
    • Визначте неузгоджені системи рівнянь, що містять три змінні.
    • Висловіть розв'язок системи залежних рівнянь, що містить три змінні.

    Джон отримав спадщину від\($12,000\) того, що він розділив на три частини і інвестував трьома способами: у фонд грошового ринку, що сплачує\(3\%\) річні відсотки; в муніципальні облігації, що сплачують\(4\%\) річні відсотки; і в пайові фонди, що виплачують\(7\%\) річні відсотки. Джон вклав\($4,000\) більше в муніципальні фонди, ніж в муніципальні облігації. Він\($670\) заробив на відсотки перший рік. Скільки Джон інвестував у кожен тип фонду?

    Малюнок\(\PageIndex{1}\): (кредит: «Елембіс», Вікісховище)

    Розуміння правильного підходу до встановлення таких проблем, як ця, робить пошук рішення питанням дотримання шаблону. Ми вирішимо цю та подібні задачі за участю трьох рівнянь і трьох змінних в цьому розділі. При цьому використовуються аналогічні методи, що використовуються для вирішення систем двох рівнянь у двох змінних. Однак пошук рішень систем трьох рівнянь вимагає трохи більшої організації та дотику візуальної гімнастики.

    Розв'язування систем трьох рівнянь у трьох змінних

    Для вирішення систем рівнянь у трьох змінних, відомих як системи три на три, основний інструмент, який ми будемо використовувати, називається гауссова елімінація, названа на честь плідного німецького математика Карла Фрідріха Гаусса. Хоча немає остаточного порядку, в якому слід виконувати операції, існують конкретні вказівки щодо того, який тип ходів може бути здійснений. Ми можемо пронумерувати рівняння, щоб відстежувати кроки, які ми застосовуємо. Мета полягає в тому, щоб усунути одну змінну за раз для досягнення верхньої трикутної форми, ідеальної форми для системи три на три, оскільки вона дозволяє для прямої зворотної заміни знайти рішення\((x,y,z)\), яке ми називаємо впорядкованою трійкою. Система у верхній трикутній формі виглядає наступним чином:

    \[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]

    Третє рівняння може бути вирішене для\(z\), а потім ми назад підставимо знайти\(y\) і\(x\). Щоб записати систему в верхньому трикутному вигляді, ми можемо виконати наступні операції:

    1. Поміняйте порядок будь-яких двох рівнянь.
    2. Помножте обидві сторони рівняння на ненульову константу.
    3. Додайте ненульове кратне одному рівнянню до іншого рівняння.

    Рішення, встановлене на систему три на три, - це впорядкована потрійна\({(x,y,z)}\). Графічно впорядкована трійка визначає точку, яка є перетином трьох площин у просторі. Візуалізувати таке перетин можна, уявивши будь-який куточок в прямокутній кімнаті. Кут визначається трьома площинами: двома суміжними стінами і підлогою (або стелею). Будь-яка точка, де зустрічаються дві стіни і підлогу, являє собою перетин трьох площин.

    КІЛЬКІСТЬ МОЖЛИВИХ РІШЕНЬ

    Рисунок\(\PageIndex{2}\) і малюнок\(\PageIndex{3}\) ілюструють можливі сценарії рішення для систем три на три.

    • Системи, які мають єдине рішення, - це ті, які після усунення призводять до набору рішень, що складається з впорядкованої трійки\({(x,y,z)}\). Графічно впорядкована трійка визначає точку, яка є перетином трьох площин у просторі.
    • Системи, які мають нескінченну кількість рішень, - це ті, які після усунення призводять до виразу, яке завжди вірно, наприклад\(0=0\). Графічно нескінченна кількість рішень являє собою пряму або збігається площину, яка служить перетином трьох площин у просторі.
    • Системи, які не мають рішення, - це ті, які після усунення призводять до твердження, яке є протиріччям, наприклад\(3=0\). Графічно система без рішення представлена трьома площинами, які не мають спільної точки.

    11.3.2.png

    Рисунок\(\PageIndex{2}\): (а) Три площини перетинаються в одній точці, представляючи систему три на три з одним розв'язком. (b) Три площини перетинаються в лінію, представляючи собою систему три на три з нескінченними розв'язками.

    11.3.3.png

    Малюнок\(\PageIndex{3}\): Всі три фігури представляють три на три системи без рішення. (а) Три площини перетинаються між собою, але не в загальній точці. (б) Дві площини паралельні і перетинаються з третьою площиною, але не один з одним. (c) Всі три площини паралельні, тому немає точки перетину.

    Приклад\(\PageIndex{1}\): Determining Whether an Ordered Triple Is a Solution to a System

    Визначте, чи\((3,−2,1)\) є впорядкована трійка рішенням системи.

    \[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]

    Рішення

    Ми перевіримо кожне рівняння, підставивши в значення впорядкованої трійки for\( x,y\), і\(z\).

    \[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1)=2 \nonumber \\[4pt] \text{True}} & {6x−4y+5z=31 \nonumber \\[4pt] 6(3)−4(−2)+5(1)=31 \nonumber \\[4pt] 18+8+5=31 \nonumber \\[4pt] \text{True} } & { 5x+2y+2z = 13 \nonumber \\[4pt] 5(3)+2(−2)+2(1)=13 \nonumber \\[4pt] 15−4+2=13 \nonumber \\[4pt] \text{True}} \end{array}\]

    \((3,−2,1)\)Впорядкована трійка дійсно є рішенням системи.

    Як: Задано лінійну систему з трьох рівнянь, розв'яжіть для трьох невідомих
    1. Виберіть будь-яку пару рівнянь і вирішуйте для однієї змінної.
    2. Виберіть іншу пару рівнянь і вирішіть для тієї ж змінної.
    3. Ви створили систему з двох рівнянь у двох невідомих. Вирішити отриману систему два на два.
    4. Назад підставляємо відомі змінні в будь-яке з вихідних рівнянь і вирішуємо для відсутньої змінної.
    Приклад\(\PageIndex{2}\): Solving a System of Three Equations in Three Variables by Elimination

    Знайдіть рішення для наступної системи:

    \[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \nonumber \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]

    Рішення

    Завжди буде кілька варіантів, з чого почати, але найбільш очевидним першим кроком тут є усунення\(x\) шляхом додавання рівнянь (1) і (2).

    \[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]

    Другий крок - множення рівняння (1) на\(−2\) і додавання результату до рівняння (3). Ці два кроки усунуть змінну\(x\).

    \[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ multiplied by }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]

    У рівняннях (4) і (5) ми створили нову систему два на два. Ми можемо вирішити для\(z\), додавши два рівняння.

    \[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \nonumber \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]

    Вибираючи по одному рівнянню з кожної нової системи, отримуємо верхню трикутну форму:

    \[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \nonumber \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]

    Далі ми спини-підставляємо\(z=2\) в рівняння (4) і вирішуємо для\(y\).

    \[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]

    Нарешті, ми можемо назад підставити\(z=2\) і\(y=−1\) в рівняння (1). Це дозволить отримати розчин для\(x\).

    \[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]

    Рішення - впорядкований потрійний\((1,−1,2)\). Див\(\PageIndex{4}\). Малюнок.

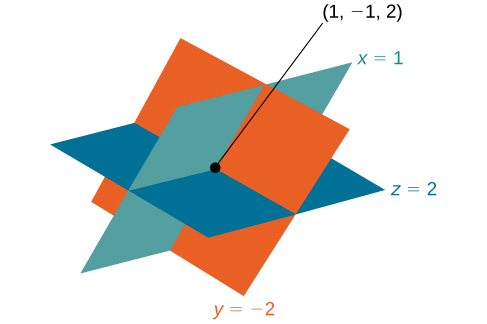
    11.3.4 пінг

    Малюнок\(\PageIndex{4}\)

    Приклад\(\PageIndex{3}\): Solving a Real-World Problem Using a System of Three Equations in Three Variables

    У проблемі, поставленій на початку розділу, Джон інвестував свою спадщину\($12,000\) у три різні фонди: частину у фонді грошового ринку, щороку сплачуючи\(3\%\) відсотки; частина в муніципальні облігації, що сплачують\(4\%\) щорічно; а решту - у пайові фонди, що сплачують\(7\%\) щорічно. Джон інвестував\($4,000\) більше в ПІФи, ніж вклав в муніципальні облігації. Загальний відсоток, зароблений за один рік, склав\($670\). Скільки він вклав у кожен вид фонду?

    Рішення

    Для вирішення цієї задачі ми використовуємо всю надану інформацію і встановимо три рівняння. Спочатку ми присвоюємо змінну кожній з трьох сум інвестицій:

    \[\begin{align} x &= \text{amount invested in money-market fund} \nonumber \\[4pt] y &= \text{amount invested in municipal bonds} \nonumber \\[4pt] z &= \text{amount invested in mutual funds} \nonumber \end{align} \nonumber\]

    Перше рівняння вказує на те, що сума трьох основних сум дорівнює\($12,000\).

    \[x+y+z=12,000 \nonumber\]

    Формуємо друге рівняння за інформацією про те, що Джон вклав в ПІФи\($4,000\) більше, ніж вклав в муніципальні облігації.

    \[z=y+4,000 \nonumber\]

    Третє рівняння показує, що загальна сума відсотків, зароблених від кожного фонду, дорівнює\($670\).

    \[0.03x+0.04y+0.07z=670 \nonumber\]

    Потім ми запишемо три рівняння як систему.

    \[\begin{align} x+y+z &=12,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \\[4pt] 0.03x+0.04y+0.07z &= 670 \nonumber \end{align} \nonumber\]

    Щоб зробити розрахунки простіше, ми можемо помножити третє рівняння на\(100\). Таким чином,

    \[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4,000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67,000 \; &(3) \nonumber \end{align} \nonumber\]

    Крок 1. Обмін рівняння (2) і рівняння (3) так що два рівняння з трьома змінними будуть вишикуватися.

    \[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] 3x+4y+7z &= 67,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

    Крок 2. Помножте рівняння (1) на\(−3\) і додайте до рівняння (2). Запишіть результат у вигляді рядка 2.

    \[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

    Крок 3. Додайте рівняння (2) до рівняння (3) і запишіть результат у вигляді рівняння (3).

    \[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] 5z &= 35,000 \nonumber \end{align} \nonumber\]

    Крок 4. Розв'яжіть для\(z\) в рівнянні (3). Назад- підставити це значення в рівнянні (2) і вирішити для\(y\). Потім назад підставити значення для\(z\) і\(y\) в рівняння (1) і вирішити для\(x\).

    \[\begin{align} 5z &= 35,000 \nonumber \\[4pt] z &= 7,000 \nonumber \\[4pt] \nonumber \\[4pt] y+4(7,000) &= 31,000 \nonumber \\[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber\]

    Джон інвестував\($2,000\) у фонд грошового ринку,\($3,000\) в муніципальні облігації та\($7,000\) в пайові фонди.

    Вправа\(\PageIndex{1}\)

    Розв'яжіть систему рівнянь в трьох змінних.

    \[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]

    Відповідь

    \((1,−1,1)\)

    Виявлення неузгоджених систем рівнянь, що містять три змінні

    Так само, як і у системах рівнянь у двох змінних, ми можемо зіткнутися з неузгодженою системою рівнянь у трьох змінних, а це означає, що вона не має рішення, яке задовольняє всім трьом рівнянням. Рівняння можуть представляти три паралельні площини, дві паралельні площини та одну площину, що перетинаються, або три площини, які перетинаються дві інші, але не в одному місці. Процес усунення призведе до помилкового твердження, типу\(3=7\) або якогось іншого протиріччя.

    Приклад\(\PageIndex{4}\): Solving an Inconsistent System of Three Equations in Three Variables

    Вирішити наступну систему.

    \[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+13z &=8 \label{4.3} \end{align} \nonumber\]

    Рішення

    Дивлячись на коефіцієнти\(x\), ми бачимо, що ми можемо усунути\(x\) шляхом додавання Equation\ ref {4.1} до Equation\ ref {4.2}.

    \[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]

    Далі множимо рівняння (1) на\(−5\) і додаємо його до рівняння (3).

    \[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{multiplied by }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \end{align} \nonumber\]

    Потім множимо рівняння (4) на 2 і додаємо його до рівняння (5).

    \[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{multiplied by }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]

    Остаточне рівняння\(0=2\) є протиріччям, тому зробимо висновок, що система рівнянь в непослідовній і, отже, не має розв'язку.

    Аналіз

    У цій системі кожна площина перетинає дві інші, але не в одному місці. Тому система непослідовна.

    Вправа\(\PageIndex{2}\)

    Розв'яжіть систему трьох рівнянь в трьох змінних.

    \[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{align} \nonumber\]

    Відповідь

    Немає рішення.

    Висловлення розв'язку системи залежних рівнянь, що містить три змінні

    З роботи з системами рівнянь у двох змінних відомо, що залежна система рівнянь має нескінченну кількість розв'язків. Те ж саме стосується залежних систем рівнянь у трьох змінних. Нескінченна кількість рішень може бути результатом декількох ситуацій. Три площини можуть бути однаковими, так що рішення одного рівняння буде рішенням двох інших рівнянь. Усі три рівняння можуть бути різними, але вони перетинаються на прямій, яка має нескінченні розв'язки. Або два рівняння можуть бути однаковими і перетинати третє на прямій.

    Приклад\(\PageIndex{5}\): Finding the Solution to a Dependent System of Equations

    Знайти розв'язку заданої системи трьох рівнянь у трьох змінних.

    \[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y+z &= 0 &(3) \nonumber \end{align} \nonumber\]

    Рішення

    По-перше, ми можемо помножити рівняння (1) на\(−2\) і додати його до рівняння (2).

    \[\begin{align} −4x−2y+6z =0 & (1) \;\;\;\;\; \text{multiplied by }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\]

    Далі нам не потрібно продовжувати. Результат, який ми отримуємо, - це ідентичність\(0=0\), яка говорить нам про те, що ця система має нескінченну кількість рішень. Є й інші способи почати розв'язувати цю систему, наприклад, множення рівняння (3) на\(−2\) та додавання його до рівняння (1). Потім ми виконуємо ті ж дії, що і вище, і знаходимо той самий результат,\(0=0\).

    Коли система залежить, ми можемо знайти загальні вирази для розв'язків. Додавши рівняння (1) і (3), ми маємо

    \[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align} \nonumber\]

    Потім вирішуємо отримане рівняння для\(z\).

    \[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]

    Назад підставляємо вираз for\(z\) в одне з рівнянь і вирішуємо для\(y\).

    \[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]

    Отже, загальне рішення є\(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\). У цьому рішенні\(x\) може бути будь-яке дійсне число. Значення\(y\) і\(z\) залежать від значення, вибраного для\(x\).

    Аналіз

    Як показано на малюнку\(\PageIndex{5}\), дві площини однакові і вони перетинають третю площину на лінії. Набір розв'язків нескінченний, оскільки всі точки вздовж лінії перетину задовольнять всім трьом рівнянням.

    Малюнок\(\PageIndex{5}\)

    Q&A: Чи завжди має бути написано загальне рішення залежної системи з точки зору\(x\)?

    Ні, ви можете написати загальне рішення з точки зору будь-якої зі змінних, але зазвичай записувати його з точки зору\(x\) і при необхідності\(x\) і\(y\).

    Вправа\(\PageIndex{3}\):

    Вирішити наступну систему.

    \[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \end{align} \nonumber\]

    Відповідь

    Нескінченна кількість розв'язків форми\((x,4x−11,−5x+18)\).

    Медіа

    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з системами рівнянь у трьох змінних.

    Key Concepts

    • A solution set is an ordered triple {(x,y,z)} that represents the intersection of three planes in space. See Example \(\PageIndex{1}\).
    • A system of three equations in three variables can be solved by using a series of steps that forces a variable to be eliminated. The steps include interchanging the order of equations, multiplying both sides of an equation by a nonzero constant, and adding a nonzero multiple of one equation to another equation. See Example \(\PageIndex{2}\).
    • Systems of three equations in three variables are useful for solving many different types of real-world problems. See Example \(\PageIndex{3}\).
    • A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction. See Example \(\PageIndex{4}\).
    • Systems of equations in three variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location.
    • A system of equations in three variables is dependent if it has an infinite number of solutions. After performing elimination operations, the result is an identity. See Example \(\PageIndex{5}\).
    • Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or two identical planes that intersect the third on a line.

    Contributors